Regressão e importância relativa
Sobre regressão e importância relativa
A regressão mostra como várias variáveis de entrada juntas afetam uma variável de saída. Por exemplo, se ambos os inputs “Anos como cliente” e “Tamanho da empresa” estiverem correlacionados com o output “Satisfação” e entre si, você poderá usar a regressão para descobrir qual dos dois inputs foi mais importante para criar a “Satisfação”
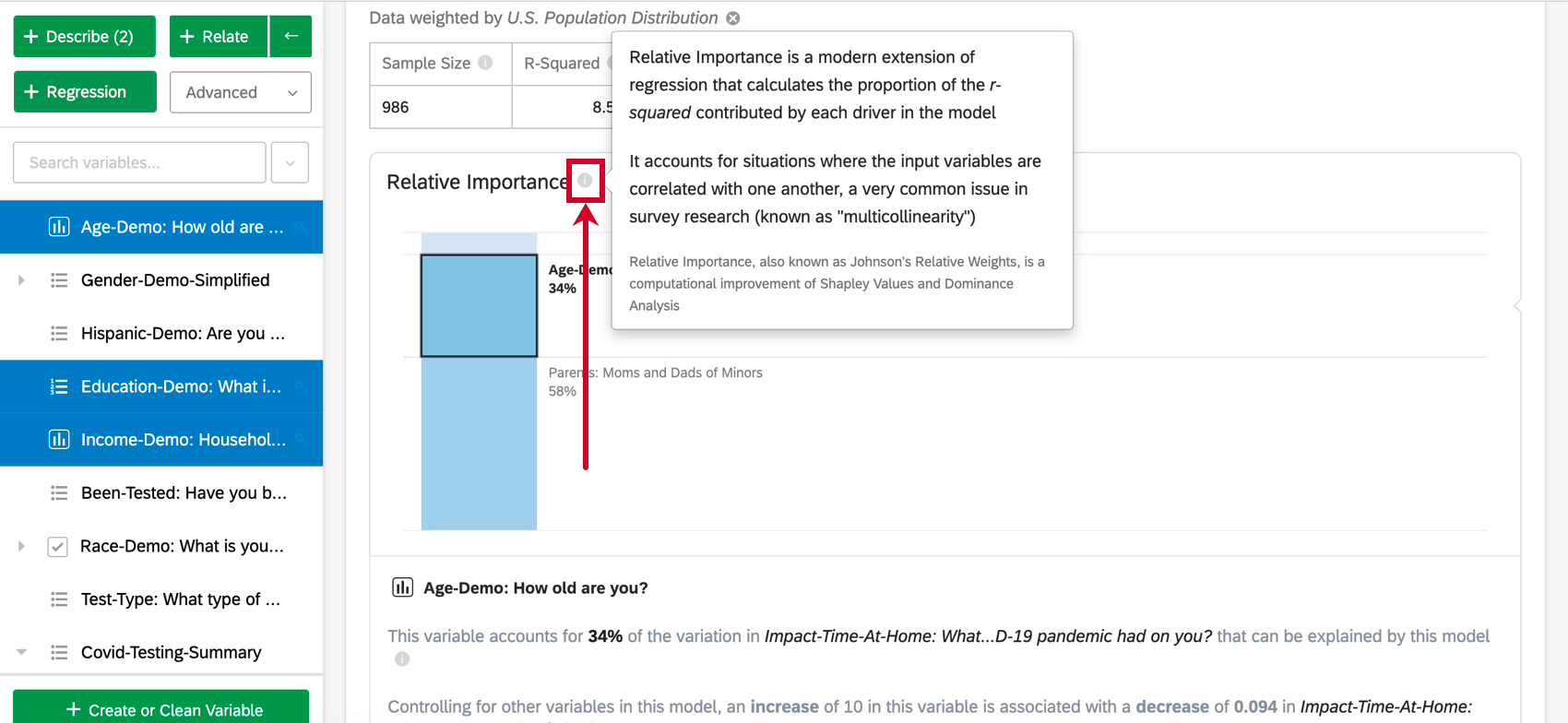
A análise de importância relativa é o método de melhores práticas para regressão em dados de pesquisa e o resultado padrão das regressões realizadas no Stats iQ. A importância relativa é uma extensão moderna da regressão que leva em conta situações em que as variáveis de entrada estão correlacionadas umas com as outras, um problema muito comum em pesquisas pesquisa (conhecido como “multicolinearidade”). A importância relativa também é conhecida como pesos relativos de Johnson, é uma variação da análise de Shapley e está intimamente relacionada à análise de dominância.
Você pode encontrar instruções abaixo sobre como configurar uma regressão no Stats iQ. Para obter mais orientações sobre como pensar nas partes analíticas da análise de regressão, consulte as páginas a seguir:
- Guia fácil de usar para regressão linear
- Interpretação de gráficos residuais para aprimorar sua regressão linear
- Guia fácil de usar para a regressão logística
- A Matriz confusão e a troca entre precisão e recordação na regressão logística
Para regressão linear, a Importância Relativa no Stats iQ segue as técnicas descritas em Lipovetsky, Stan & Conklin, Michael. (2001). Análise de regressão na abordagem da teoria dos jogos. Applied Stochastic Models in Business and Industry (Modelos estocásticos aplicados nos negócios e na indústria). 17. 319 – 330. 10.1002/asmb.446.
Para regressão logística, a Importância relativa no Stats iQ segue as técnicas descritas em Tonidandel, Scott & LeBreton, James. (2009). Determinação da importância relativa dos preditores na regressão logística: An Extension of Relative Weight Analysis (Uma extensão da análise de peso relativo). Métodos de pesquisa organizacional – MÉTODOS DE PESQUISA ORGANIZACIONAL. 12. 10.1177/1094428109341993.
Seleção de variáveis para cartões de regressão
A criação de um cartão de regressão permitirá que você entenda como o valor de uma variável em seu conjunto de dados é afetado pelos valores de outras.
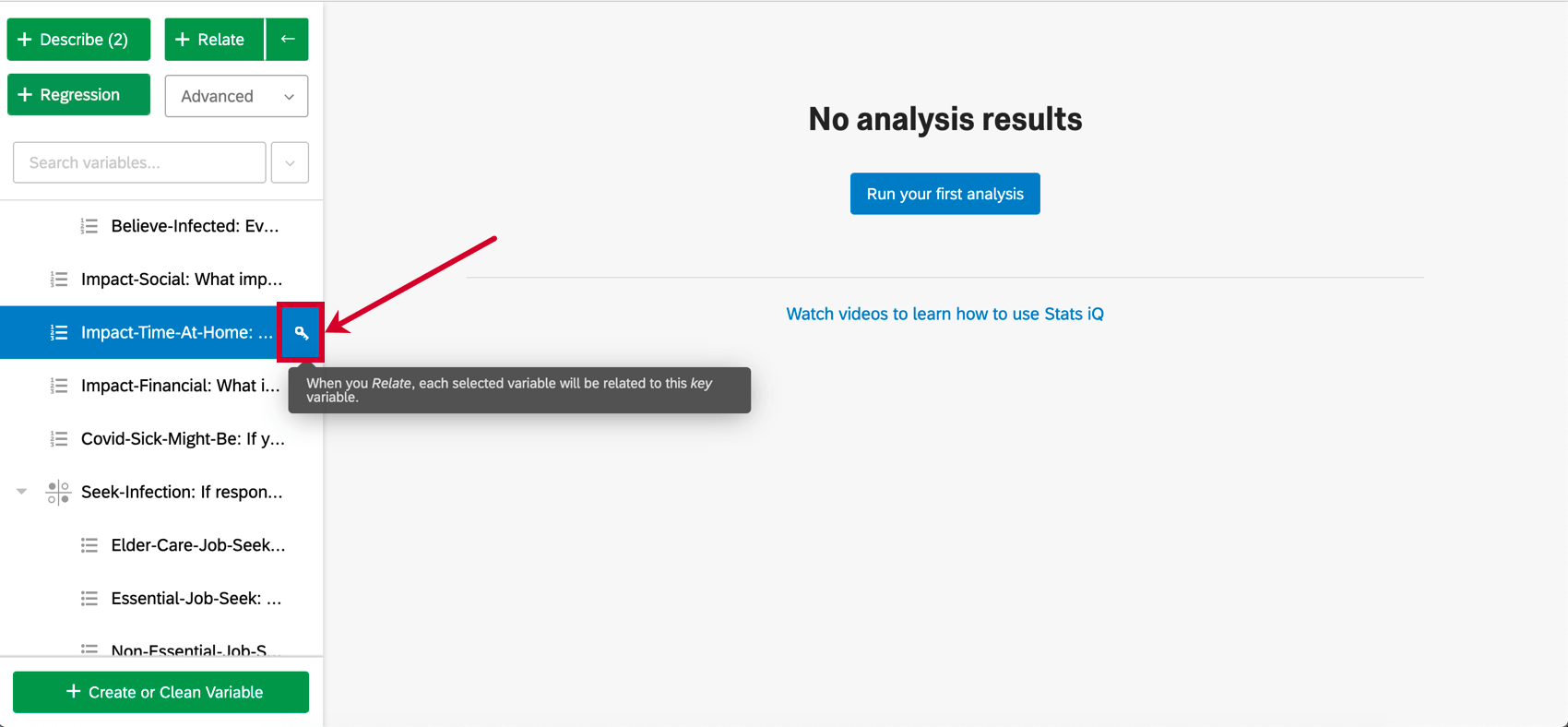
Ao selecionar variáveis, uma variável terá uma chave junto a ela. Para regressão, a variável principal será a variável de saída. Cada outra variável selecionada após a variável principal será uma variável de entrada. Em outras palavras, estamos tentando explicar como o valor da variável de saída é determinado pelas variáveis de entrada.
Aspectos a serem considerados ao selecionar variáveis para regressão:
- Você pode alterar a variável principal clicando no ícone de chave avançar de qualquer variável no painel de variáveis.
- Se forem selecionadas mais variáveis do que o número de respostas que você tem, a regressão não será executada.
- Você pode selecionar até 25 variáveis de entrada. No entanto, você deve tentar selecionar de 1 a 10 variáveis de entrada, ou seus resultados poderão ficar muito complicados.
Se você tiver um grande número de variáveis que gostaria de incluir em uma análise, considere as seguintes abordagens:
- Execute algumas regressões iniciais e exclua as variáveis que têm pouca importância no modelo.
- Combinar diversas variáveis, por exemplo, calculando a média delas.
- Se a estrutura dos seus dados permitir, você poderá usar um processo de importância relativa de duas etapas, conforme descrito na página 341 aqui.
Exemplo: Por exemplo, imagine que você tenha dez medidas de satisfação com a autonomia colaborador e dez medidas de satisfação com a remuneração colaborador.
- Faça a média desses grupos em duas variáveis resumidas diferentes – uma para autonomia e outra para remuneração.
- Execute uma análise de importância relativa com a satisfação geral como resultado e as duas variáveis de resumo como entrada para ver qual grupo é mais importante.
- Em seguida, execute uma análise de importância relativa com a satisfação geral como resultado e apenas as dez variáveis de autonomia como entradas para ver quais são as mais importantes dentro desse grupo.
- Execute uma análise de importância relativa com a satisfação geral como resultado e apenas as dez variáveis de remuneração como entradas para ver quais são as mais importantes dentro desse grupo.
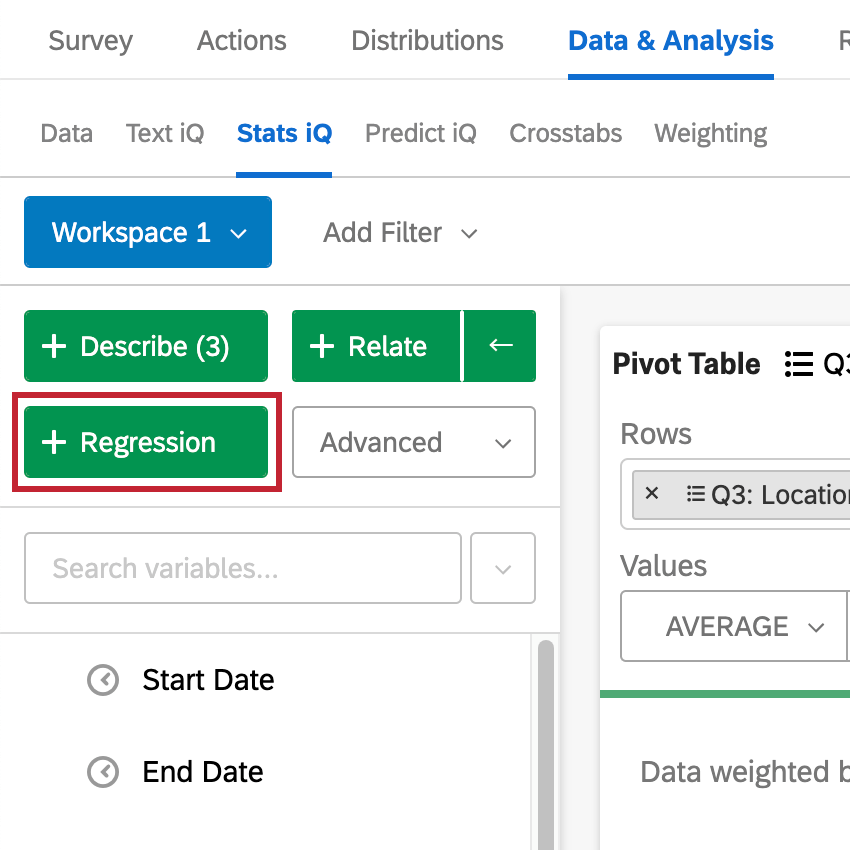
Depois de selecionar suas variáveis, clique em Regression (Regressão ) para executar uma regressão.
Qdica: na parte superior do cartão de regressão, haverá uma linha verde (e, às vezes, vermelha). Se você clicar nele, verá a quantidade de respostas marcadas como “Incluídas” ou “Ausentes” para esse cartão específico.
- Incluídos: Os entrevistados que responderam à pergunta para cada pergunta ou ponto de dados usado na análise de regressão, ou tiveram seus dados para variáveis de entrada ausentes imputados. Esses dados serão usados na análise de regressão.
- Ausente: Os entrevistados que não têm um valor para a variável dependente do resultado. Esses dados não serão usados na análise de regressão.
Tipos de regressão
Há dois tipos principais de regressão executados no Stats iQ. Se a variável de saída for uma variável numérica, Stats iQ executará uma regressão linear. Se a variável de saída for uma variável de categoria, Stats iQ executará uma regressão logística.
Mais especificamente, os tipos de regressão que Stats iQ executará são os seguintes:
Regressão linear
A importância relativa é combinada com o método dos mínimos quadrados ordinários (OLS). O resultado vem de uma combinação das duas análises:
- Importância relativa: Tudo nesta seção vem da Importância relativa, exceto o r-quadrado, que vem da regressão OLS.
- Explore o modelo em detalhes: Tudo nesta seção vem da Relative Importance, exceto as distribuições, que são extraídas dos próprios dados.
- Analise os diagnósticos e os resíduos da regressão OLS para aprimorar seu modelo: Tudo nesta seção vem da regressão OLS.
Regressão Logística
A regressão logística é um método de classificação binária usado para entender os motivadores de um resultado binário (por exemplo, sim ou não) com base em um conjunto de variáveis de entrada. Se você executar uma regressão em uma variável de output com mais de dois grupos, Stats iQ selecionará um grupo e agrupará os outros de forma a torná-lo uma regressão binária (você pode alterar qual grupo está sendo analisado após a execução da regressão).
Importância relativa
As variáveis de entrada nos dados pesquisa geralmente estão altamente correlacionadas umas com as outras; esse é um problema chamado “multicolinearidade” Isso pode levar a resultados de regressão que aumentam artificialmente a importância de uma variável e diminuem a importância de outra variável correlacionada. A importância relativa é reconhecida como o método de prática recomendada para levar isso em conta.
A importância relativa (especificamente os pesos relativos de Johnson) não sofre desse problema e equilibrará adequadamente a importância das variáveis de entrada, independentemente do tipo de regressão que estiver sendo executado. Ele também calcula o peso relativo de cada variável (ou importância relativa), a proporção da variação explicável no resultado devido a essa variável. Isso é mostrado como uma série de porcentagens que somam 100%.
Ele retorna resultados semelhantes à execução de uma série de regressões, uma para cada variação das variáveis de entrada. Por exemplo, se você tivesse duas variáveis, ele faria o equivalente a executar três regressões: uma com a variável A, outra com a variável B e outra com ambas. Isso permite quantificar a importância de cada variável e aplicar essa quantificação de volta ao resultado da regressão.
Saída de regressão
Quando você executa uma regressão no Stats iQ, resultados da análise contêm as seguintes seções:
Resumo numérico
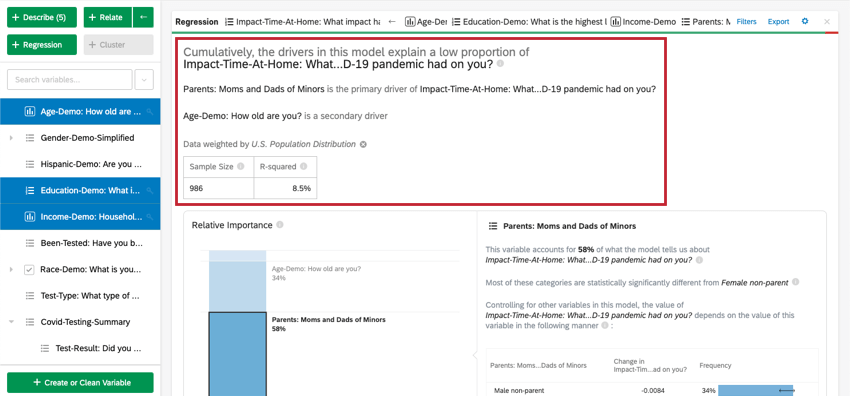
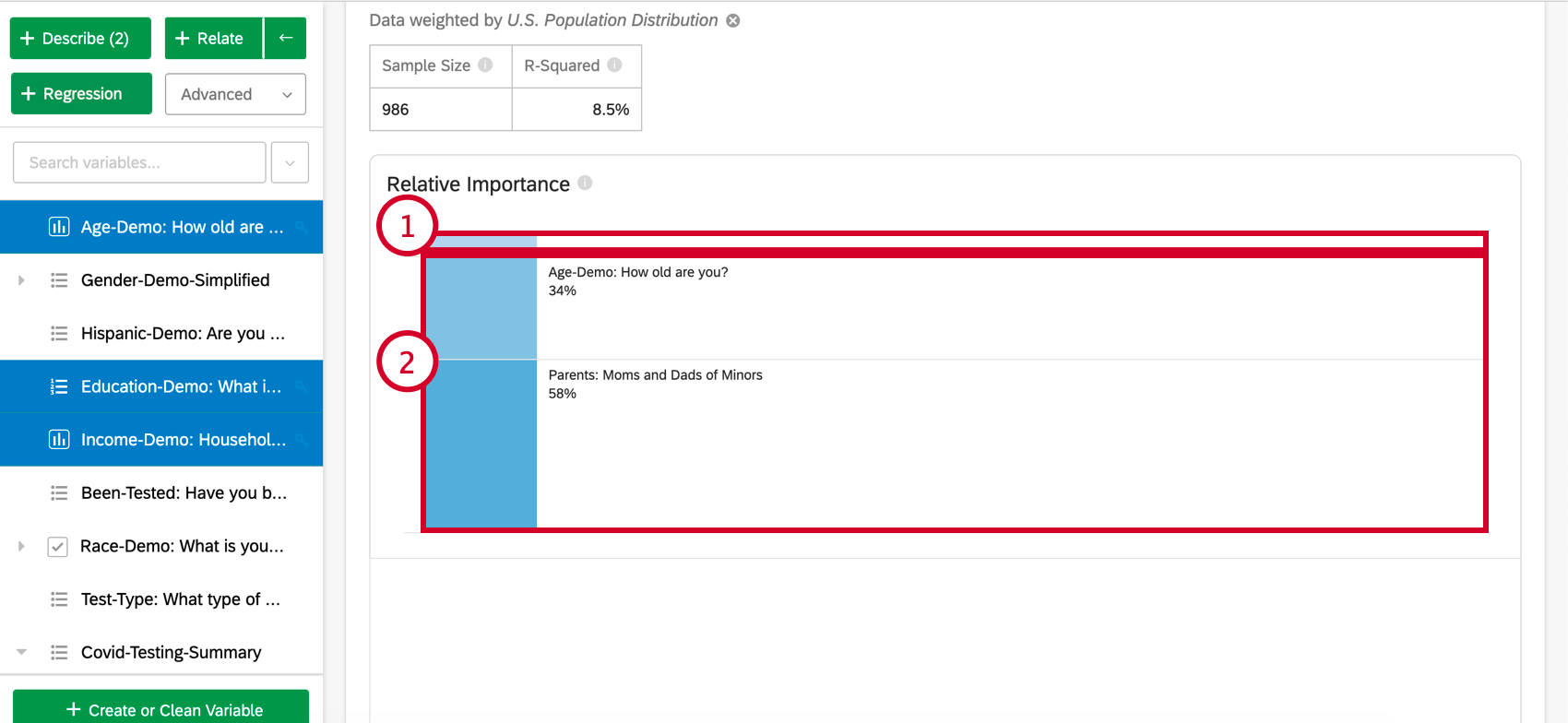
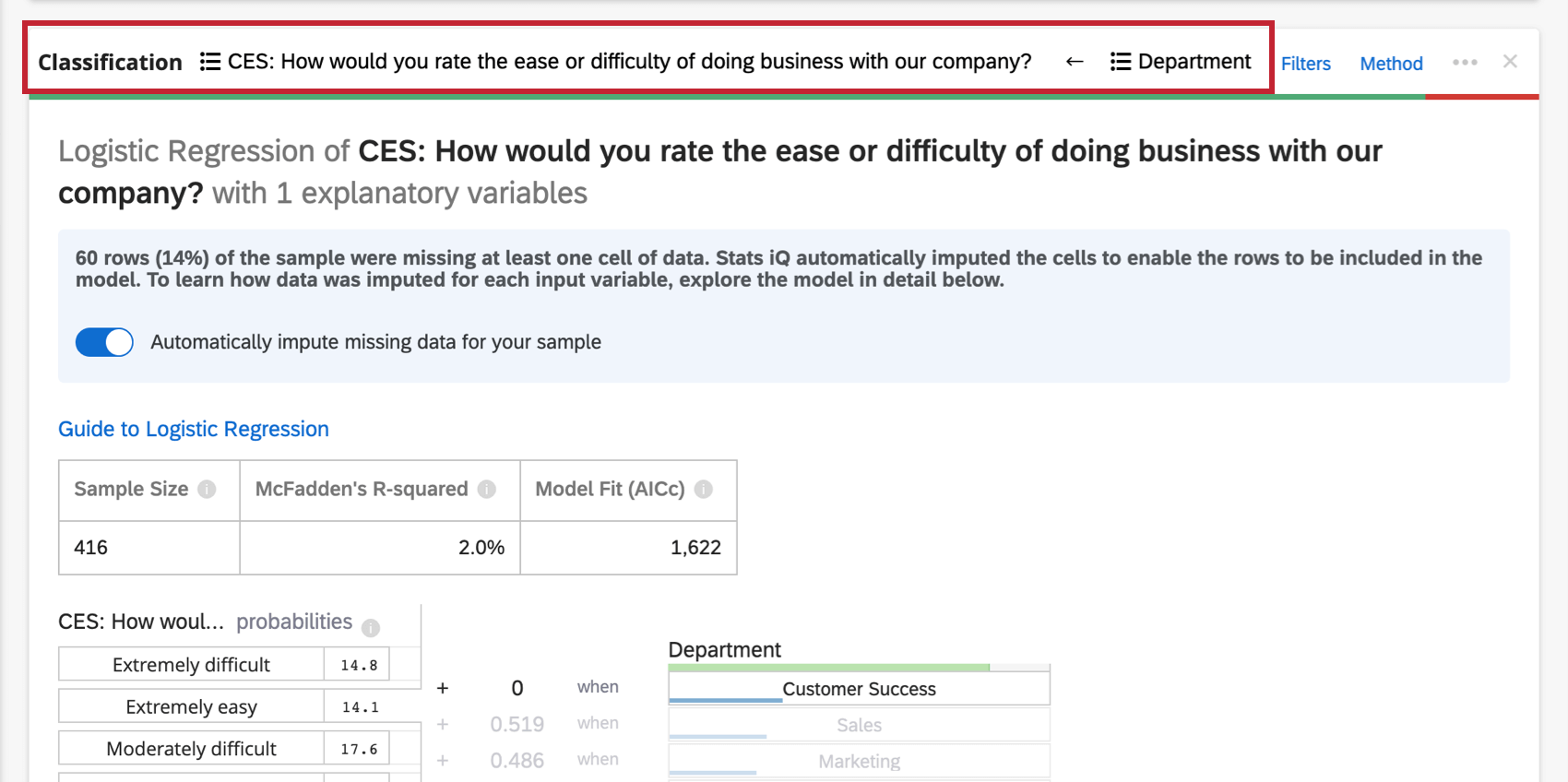
Na parte superior do cartão, há um resumo da análise de regressão. Observando as variáveis escolhidas, este resumo escrito explica quais variáveis são os principais e os secundários, bem como os que tiveram baixo impacto cumulativo. A tabela de dados inclui o tamanho Amostra e o valor R-quadrado.
Importância relativa
- Variáveis de baixo impacto: As variáveis que individualmente têm uma importância relativa de 10% ou menos serão agrupadas. Quando selecionada, haverá uma seção explicando a importância relativa e a significância estatística de cada variável de baixo impacto.
- Variáveis de alto impacto: Cada variável de alto impacto será separada e clicável. Depois que uma variável for selecionada, abaixo do gráfico de barras, você poderá visualizar a variação contabilizada e o que aconteceria se outras variáveis fossem controladas no modelo.
Detalhes adicionais do modelo
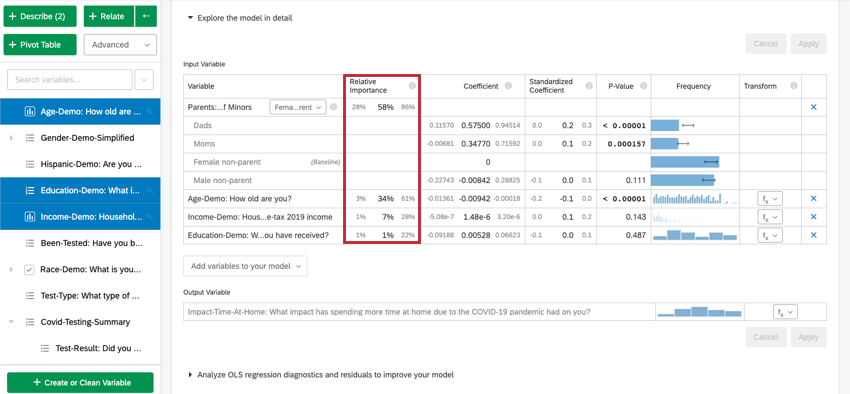
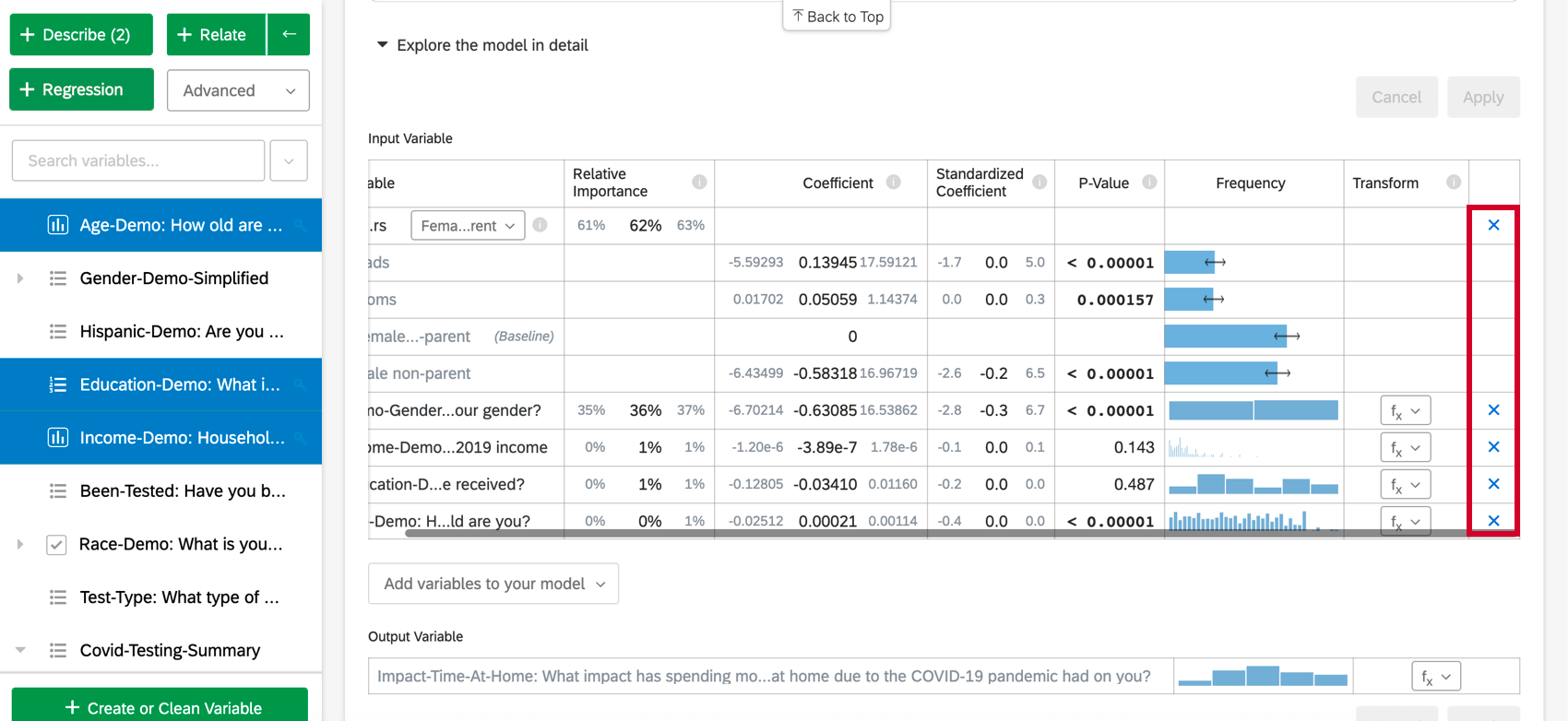
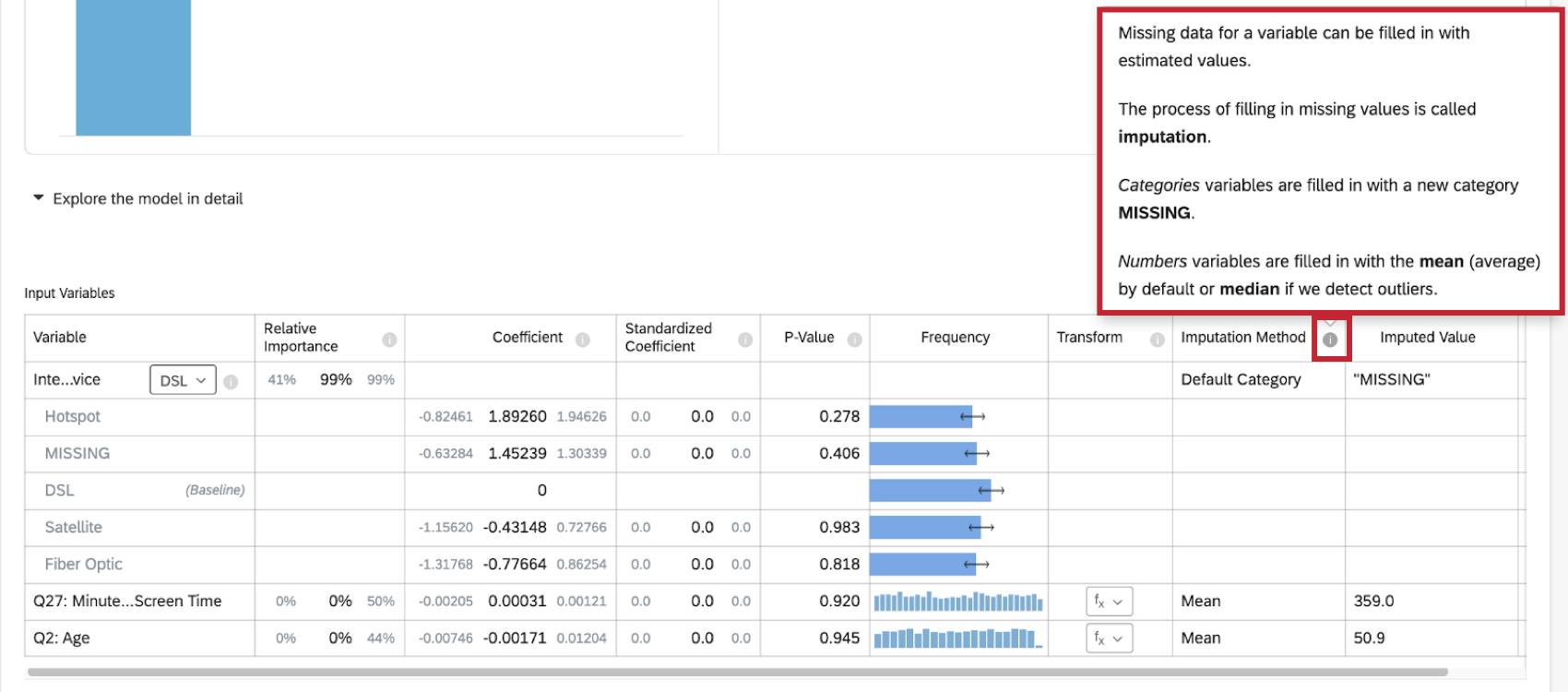
Ao selecionar Explore the model in detail (Explorar o modelo em detalhes), você verá as variáveis de entrada e a variável de saída listadas. Suas variáveis de entrada virão com as seguintes informações:
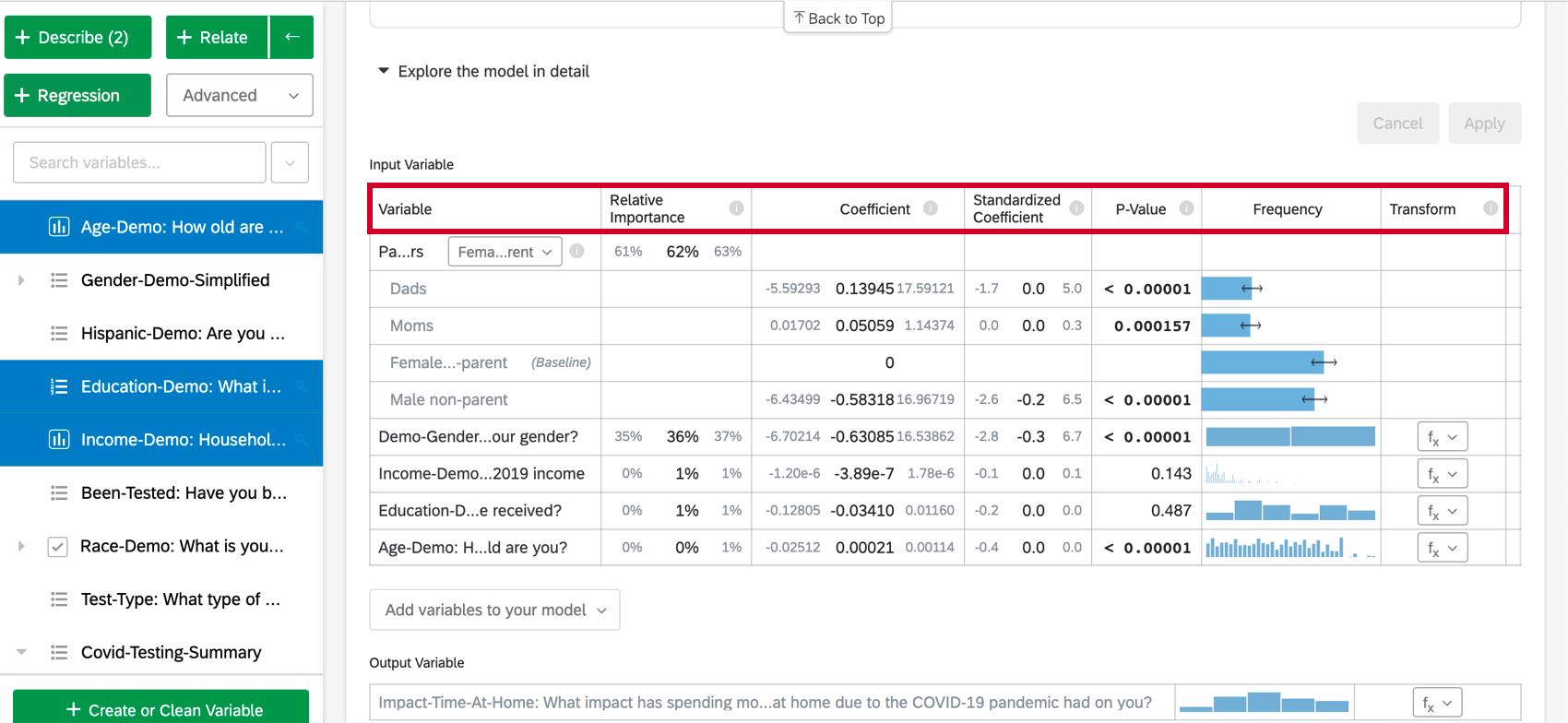
- Importância relativa: A proporção do r-quadrado que é contribuída por uma variável individual. O r-quadrado é a proporção da variação da variável de resultado que pode ser explicada pelas variáveis de entrada nesse modelo. Consulte Importância relativa para obter mais detalhes.
- Razão de chances: Relevante apenas para a regressão logística. A razão de chances de uma determinada variável de entrada indica o fator pelo qual as chances mudam para cada aumento unitário na variável explicativa.
Exemplo: Por exemplo, se a razão de chances da Satisfação com o Gerente for 1,1 e os grupos da variável de saída forem Satisfeito e Não satisfeito, então, para cada instância em que a Satisfação com o Gerente for 1 maior, a chance de a variável de saída ser Satisfeito será 1,1 maior (10% maior). Se a linha de dados for uma categoria, como cor[azul], o coeficiente representará a alteração nas chances da variável de resposta se a variável de categorias for essa categoria específica (azul) em vez do grupo de “linha de base” (vermelho, verde etc.).
- Coeficiente: Cada aumento de 1 unidade em uma variável de entrada está associado a um aumento do coeficiente na variável de saída. Esses coeficientes são construídos com base nos resultados da análise de importância relativa e, portanto, ajustam a multicolinearidade e não correspondem aos coeficientes que resultariam de uma regressão padrão de mínimos quadrados ordinários.
- Coeficiente padronizado: O coeficiente padronizado é o coeficiente dividido pela variação da variável de entrada. Isso coloca cada variável na mesma escala para que seus coeficientes possam ser comparados mais diretamente.
- Valor de p: O valor p é a medida de significância estatística. Valores mais baixos estão associados a menores chances de que o relação seja uma coincidência. Para variáveis categóricas, o valor de p indica a significância estatística da diferença entre um grupo e o grupo de “linha de base” na variável.
- Transformar: Consulte Transformação de variáveis.
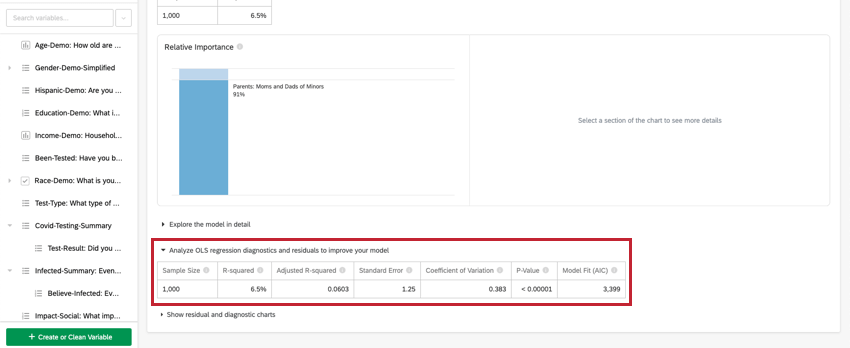
Análise de regressão OLS
Para regressão linear, clique em Analyze OLS regression diagnostics and residuals (Analisar diagnósticos e resíduos de regressão OLS) para aprimorar seu modelo abaixo da variável-chave/de saída para visualizar os gráficos Predicted vs. Actual e Residuals (Previsto vs. Real e Resíduos). Consulte Interpretação de gráficos residuais para melhorar sua regressão para obter mais informações.
Variável incluída
Ao longo do cabeçalho superior do cartão de regressão, você verá as variáveis usadas na regressão.
Clique no nome de uma variável para abrir uma nova janela na qual você pode recodificar ou baldear valores. Clique nas setas para alternar quais são as variáveis de entrada e quais são as variáveis de saída na análise.
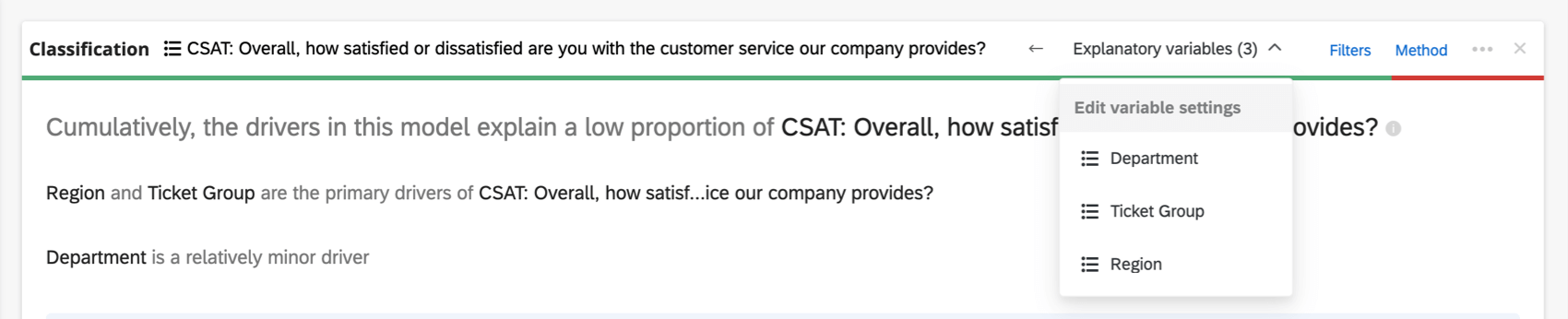
Se houver muitas variáveis envolvidas para serem exibidas no cabeçalho, haverá um menu suspenso Variáveis explicativas em que você poderá escolher entre as variáveis que deseja recodificar.
Adição e remoção de variáveis
Depois de criar um cartão de regressão, você pode adicionar outras variáveis à análise seguindo as etapas abaixo:
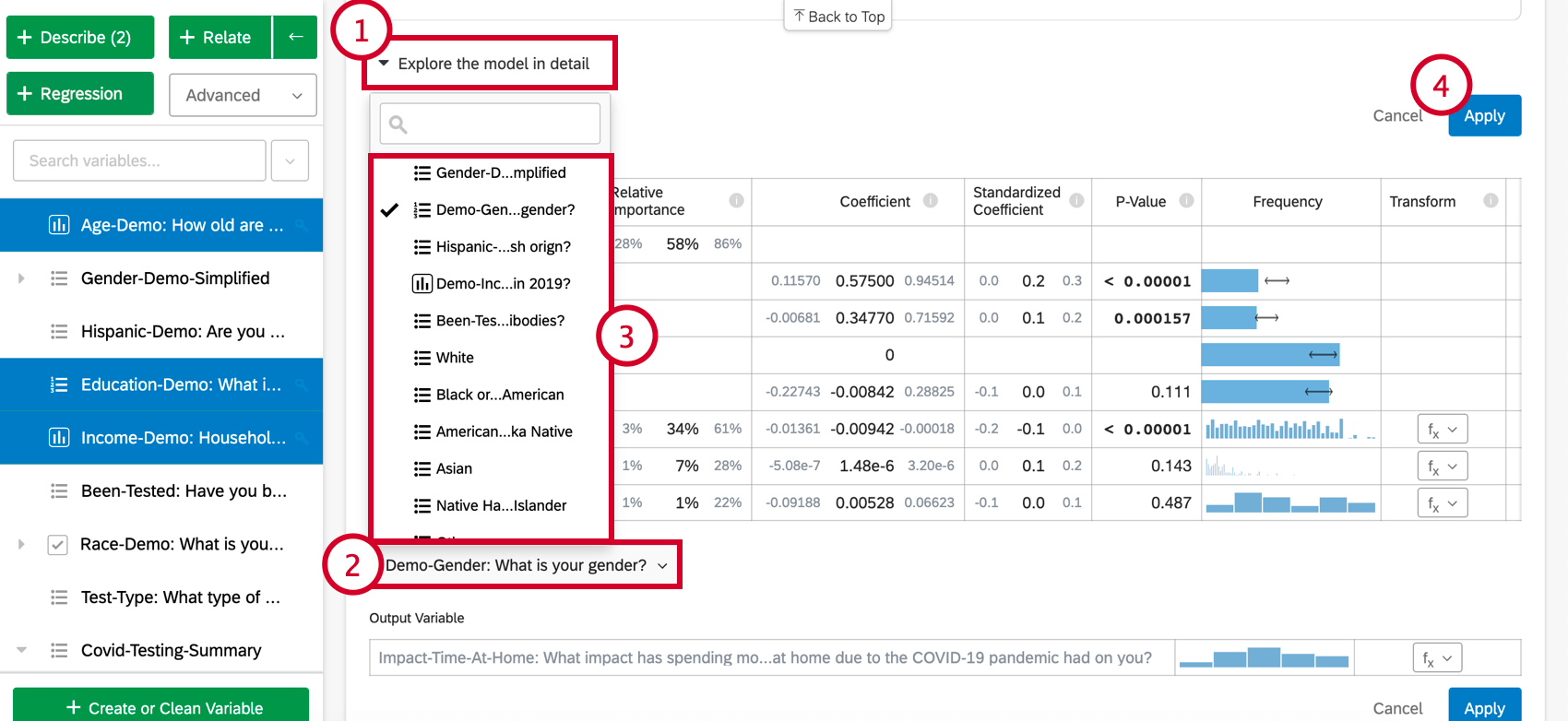
- Clique em Explore the model in detail (Explorar o modelo em detalhes).
- Selecione Adicionar variáveis ao seu modelo na parte inferior do cartão. Isso exibirá uma lista de variáveis que ainda não foram usadas na regressão.
- Escolha uma variável dessa lista.
- Clique em Aplicar ) para executar a análise novamente com a nova variável incluída.
Para remover uma variável da regressão, passe o mouse sobre a variável desejada e clique no X azul no lado direito da tabela. Depois de escolher as variáveis a serem adicionadas ou removidas, certifique-se de selecionar “Aplicar” ) para executar o novo modelo.
Imputação de variáveis
A regressão só considerará as linhas em que todas as variáveis de entrada tiverem dados. No entanto, muitas vezes faltam dados na coleta de dados pesquisa, o que pode afetar negativamente a análise de regressão e o modelo. Se você incluir apenas linhas sem dados ausentes na regressão, resultados da análise poderão ser tendenciosos porque a amostra não é representativa de todo o conjunto de dados.
Com a imputação, Stats iQ preencherá automaticamente os dados ausentes com valores estimados. Quando os dados ausentes são preenchidos, é possível incluir mais dados originais na análise de regressão, resultando em um modelo de regressão com menos viés que pode explicar melhor a variação na variável de resultado desejada.
A imputação é automática, portanto, quando você executa uma análise de regressão em um conjunto de dados com valores ausentes, o conjunto de dados será imputado antes que qualquer cálculo seja feito.
- Clique aqui para ver um exemplo de conjunto de dados antes e depois da imputação de variáveis.
- Antes da imputação:
Para essa regressão, “Uso de dados” é a variável de resultado e “Idade”, “Serviço de Internet” e “Minutos de tempo de tela” são as variáveis de entrada.ID da linha Uso de dados Idade Serviço de Internet Tempo de tela (minutos) 1 75 39 Satélite 503 2 19 41 Fibra óptica 52 3 87 434 4 54 23 Satélite 5 14 101 6 75 Satélite 7 81 57 DSL 329 Atenção: Se você executasse uma regressão sem preencher os valores ausentes, apenas as linhas 1, 2 e 7 seriam incluídas.Após a imputação:
ID da linha Uso de dados Idade Serviço de Internet Tempo de tela (minutos) 1 75 39 Satélite 503 2 19 41 Fibra óptica 52 3 87 50.9 FALTANDO 434 4 54 23 Satélite 359.0 5 14 50.9 FALTANDO 101 6 75 50.9 Satélite 359.0 7 81 57 DSL 329 Qdica: “Internet Service” é uma variável categórica, não numérica, portanto, o valor ausente é preenchido como “MISSING”.
Métodos de imputação
Atualmente, Stats iQ usa os seguintes métodos de imputação:
- Categoria padrão: Stats iQ criará um novo valor de categoria “MISSING” para preencher os dados ausentes. Esse método é usado para variáveis categóricas.
- Média: Se Stats iQ não detectar nenhum valor atípico na distribuição da variável numérica, os dados ausentes da variável serão preenchidos com o valor médio (average). Esse método é usado para variáveis numéricas.
- Mediana: Se Stats iQ detectar outliers na distribuição da variável numérica, os dados ausentes da variável serão preenchidos com o valor mediano. Esse método é usado para variáveis numéricas.
Indicadores de imputação
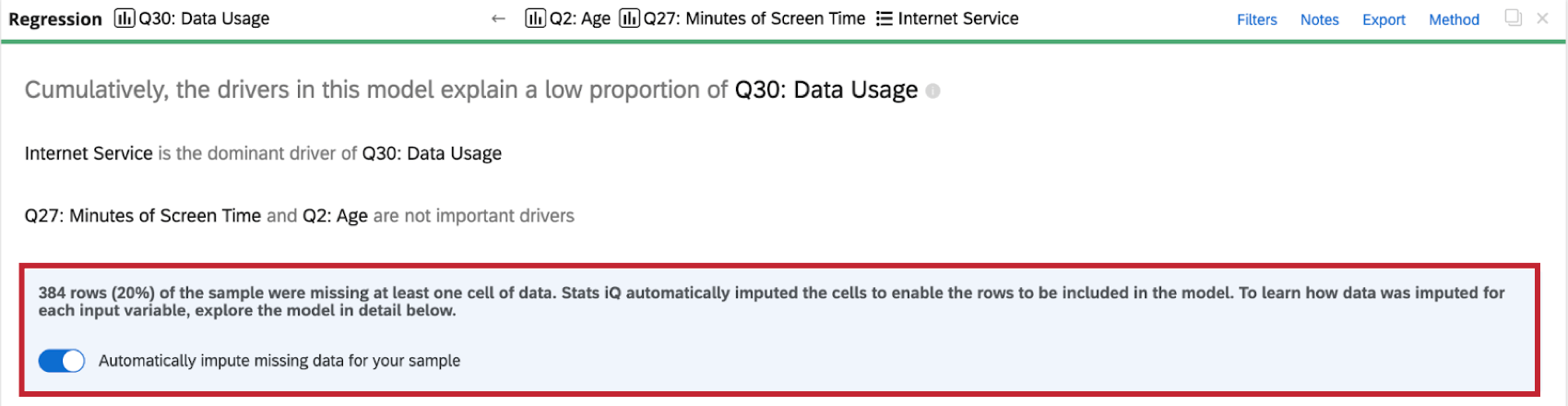
Ao realizar uma análise de regressão no conjunto de dados, você verá um indicador de imputação na parte superior do cartão de regressão.
Mais informações sobre a imputação estão disponíveis clicando no símbolo de informação ( i ) avançar de Imputation Method.
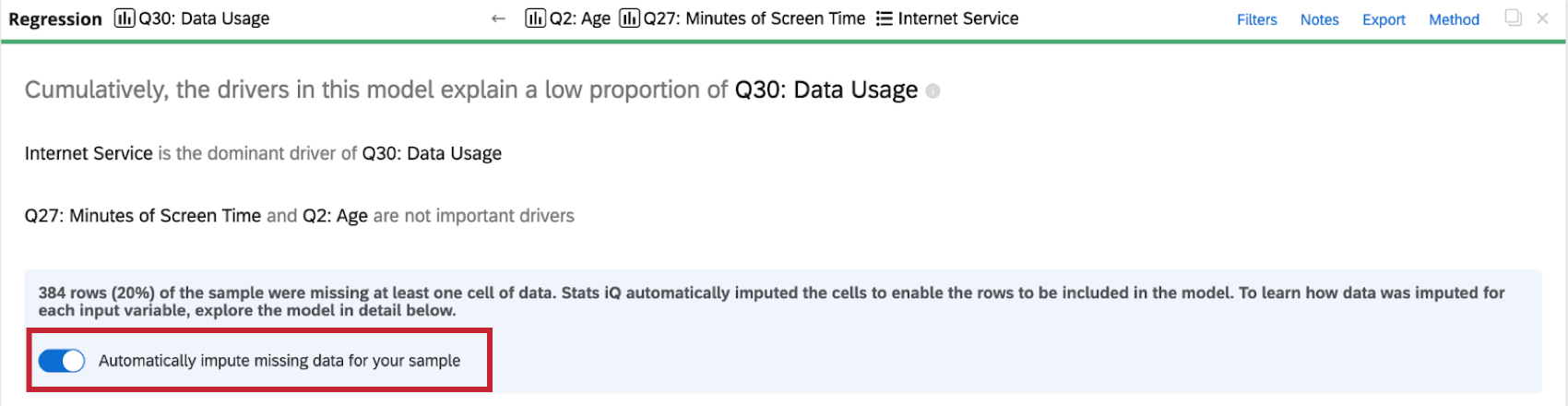
Desativação da imputação
Stats iQ aplica automaticamente a imputação a todos os cartões de regressão. Para desativar a imputação automática, clique em Automatically impute missing data for your amostra (Imputar automaticamente dados ausentes para sua amostra ) na parte superior do cartão de regressão.
Avisos de imputação
- Se muitos dados forem imputados, seu modelo de regressão se tornará tendencioso e não confiável. Quando mais de 50% do seu conjunto de dados tiver sido preenchido, Stats iQ o avisará sobre a possibilidade de tirar conclusões dos resultados da regressão.

- Quando forem detectados outliers em qualquer uma das variáveis de entrada numéricas, Stats iQ imputará as variáveis usando o valor mediano em vez da média. Nesse cenário, Stats iQ o avisará quando você explorar o modelo em detalhes.

Transformando variáveis
Ao executar uma análise de regressão no Stats iQ, você pode descobrir que precisa melhorar o modelo. A maneira mais comum de aprimorar um modelo é transformar uma ou mais variáveis, geralmente usando um “log” ou outra transformação funcional.
A transformação de uma variável muda a forma de sua distribuição. Em geral, os modelos de regressão funcionam melhor com distribuições mais simétricas e em forma de sino. Experimente diferentes tipos de transformações até encontrar uma que lhe proporcione esse tipo de distribuição.
Para transformar uma variável:
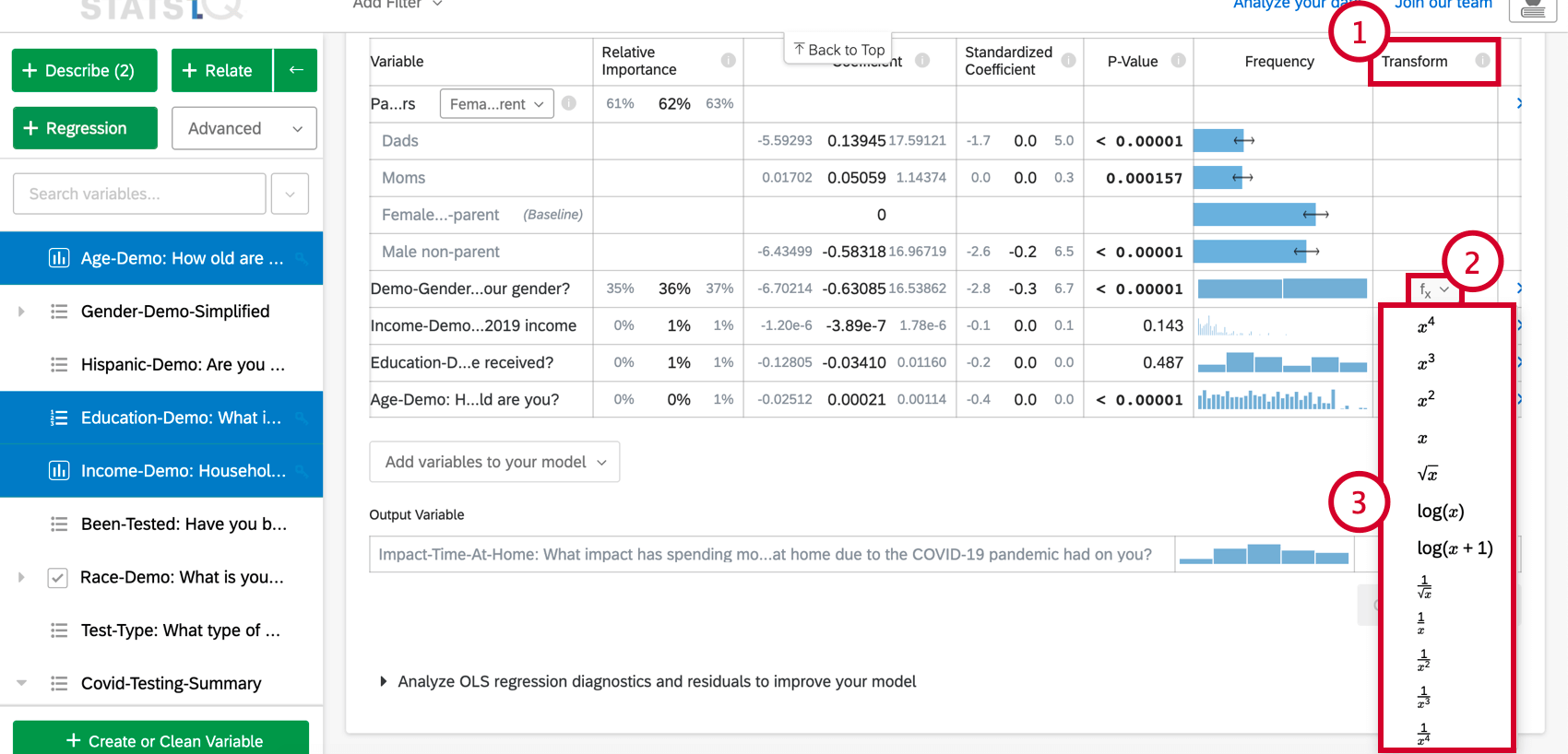
- Na opção Explorar o modelo em detalhes, role até a coluna Transformar .
- Clique no botão da função(f(x)) para a variável que você deseja transformar.
- Na lista, escolha a função que você gostaria de aplicar e o Stats iQ recalculará o cartão usando a nova variável transformada.
As seguintes transformações estão disponíveis no Stats iQ:
De longe, a transformação mais comum é log(x). Ele transforma uma distribuição de “potência” (como o tamanho da população da cidade), que tem muitos valores menores e um pequeno número de valores maiores, em uma ” distribuição normal” em forma de sino (como a altura), em que a maioria dos valores está agrupada no meio.
Use log(x+1) se a variável que está sendo transformada tiver alguns valores de zero, pois log(x) não pode ser calculado quando x é zero.
Para obter mais detalhes sobre quando transformar suas variáveis, consulte Interpreting Residual Plots to Improve Your Linear Regression (Interpretando gráficos residuais para melhorar sua regressão linear)
Outras técnicas de regressão linear disponíveis no Stats iQ
A Importância Relativa combinada com Mínimos Quadrados Ordinários é a saída padrão para uma regressão linear. No entanto, há outras opções disponíveis.
Para acessar M-estimation, Ordinary Least Squares e Ridge Regression, clique na engrenagem de configurações no canto superior direito do seu cartão de regressão. Ao clicar no nome da técnica de regressão em Métodos de regressão , você poderá alterar a técnica de regressão usada para o cartão de regressão. Isso só pode ser feito para regressão linear.

- M-estimação: Projetada para lidar com outliers na variável de saída melhor do que o Ordinary Least Squares (OLS).
- Mínimos quadrados ordinários: Os mínimos quadrados ordinários (OLS) são a técnica de regressão clássica. Ele é sensível a discrepâncias e outras violações em suas suposições, por isso recomendamos métodos mais robustos, como a estimativa M. Como o OLS é usado no resultado padrão da importância relativa, você só deve selecionar essa opção se estiver interessado nos recursos que ainda não foram adaptados ao resultado da importância relativa: previsão de resultados e adição de termos de interação.
- Regressão Ridge: A regressão Ridge é uma técnica semelhante à regressão OLS padrão, mas com um parâmetro de ajuste alfa. Esse parâmetro alfa ajuda a lidar com a alta variação e com dados que sofrem de multicolinearidade. Quando ajustada adequadamente, a regressão de cumeeira geralmente produz previsões melhores do que a OLS, devido a um melhor compromisso entre a tendência e a variação. No Stats iQ, você poderá escolher o parâmetro alfa ao usar a regressão de cumeeira.
Depois de selecionar M-estimation, Ordinary Least Squares ou Ridge Regression, você poderá ver o resultado. O resultado aparecerá abaixo da seção Regression Methods (Métodos de regressão ).
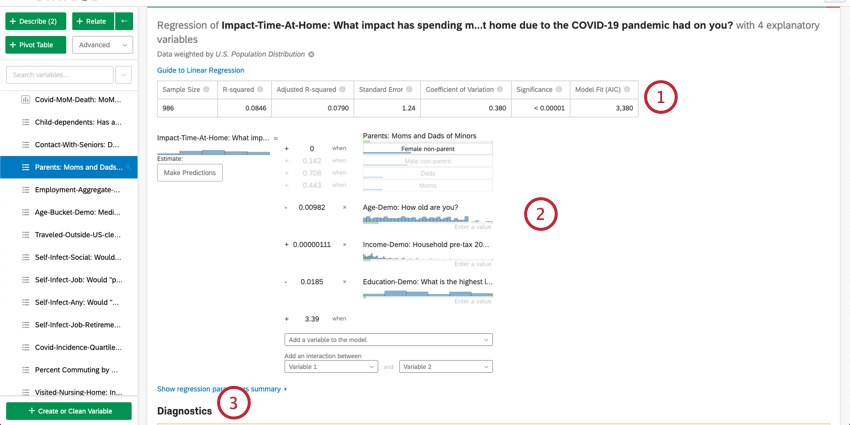
- Resumo numérico: Na parte superior do cartão, há um resumo da análise de regressão. Isso inclui o tamanho Amostra, casos ausentes, método, valor de R-quadrado, erro padrão, coeficiente de variação e ajuste do modelo.
- Detalhes do coeficiente: Os principais resultados da regressão, a equação matemática, estão abaixo do resumo. A variável principal de saída/chave está à esquerda da equação. As variáveis de entrada estão no lado direito. Passar o mouse sobre uma variável exibe uma dica de ferramenta que explica em termos simples como essa variável contribui para a variável de saída. Aqui, você também pode inserir valores na equação matemática para estimar os valores da sua variável de saída. Consulte a seção abaixo sobre estimativa de valores de variáveis de saída para obter mais informações.
- Diagnósticos e resíduos: Stats iQ fornece diagnósticos para ajudá-lo a avaliar a precisão e a validade do seu modelo. Para saber mais, consulte Interpretação de gráficos residuais para aprimorar sua regressão linear ou A Matriz de confusão e a troca entre precisão e recordação na regressão logística.
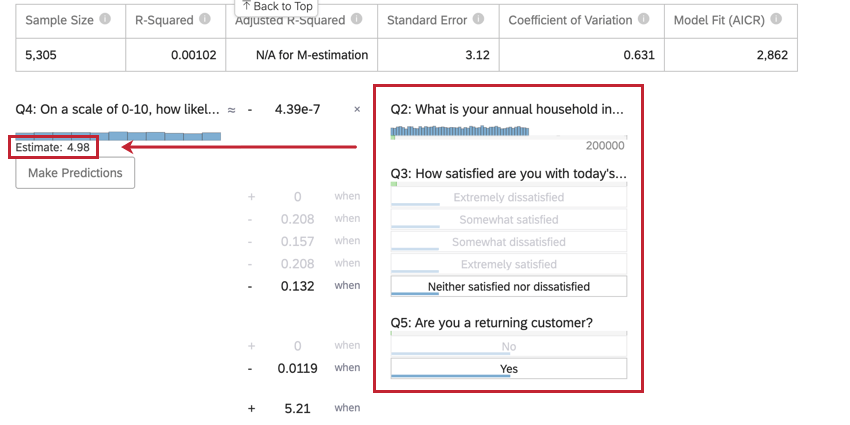
Estimativa de valores de variáveis de saída
Depois de executar uma regressão, você poderá usar a equação matemática na seção Detalhes do coeficiente para estimar os valores da variável de saída com base nos valores de entrada selecionados. No lado direito da equação, você verá suas variáveis de entrada. Você pode definir valores para cada uma de suas variáveis de entrada. No lado esquerdo da equação está sua variável de saída. Depois de inserir valores para as variáveis de entrada, a equação calculará uma estimativa para a variável de saída com base no modelo de regressão.
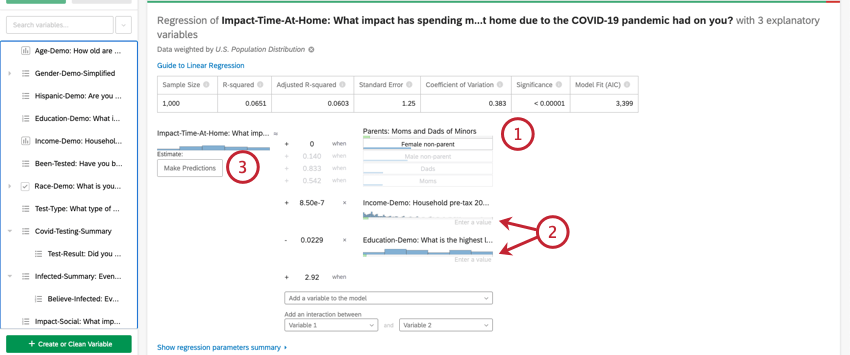
- Essa variável de entrada é uma variável de tipo de categoria. Para inserir um valor para as variáveis de categoria, clique no valor desejado na lista de opções.
- Essas variáveis de entrada são do tipo numérico. Para inserir um valor para variáveis numéricas, clique em Enter a value (Inserir um valor ) e digite um número.
- Essa variável é a variável de saída de sua equação de regressão. Depois de selecionar os valores para as variáveis de entrada, um valor estimado para a variável de saída aparecerá avançar de onde está escrito Estimate (Estimativa).
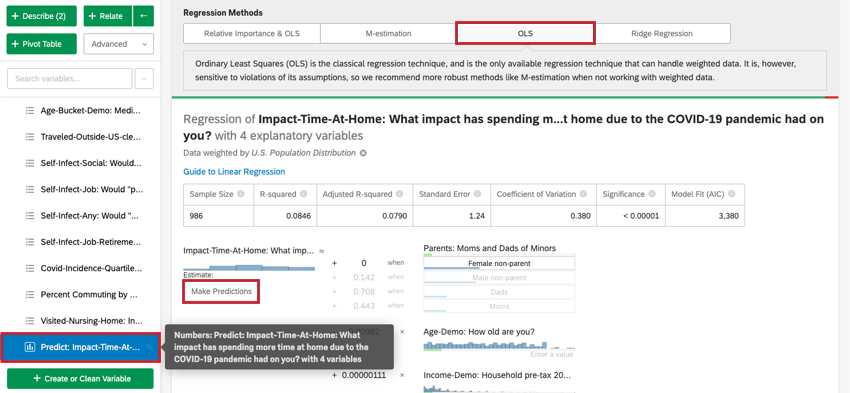
Previsão de resultados
Normalmente, você usará a análise de regressão no Stats iQ para entender a relação entre as variáveis de entrada e as variáveis de saída. No entanto, depois que um modelo de regressão é criado, ele também pode ser usado para prever o valor de saída para linhas de dados em que você tem valores para os inputs.
Termos de interação e outras preocupações avançadas
Adição de termos de interação
Ao procurar melhorar seu modelo de regressão, talvez você queira adicionar termos de interação além das variáveis de entrada existentes. Um termo de interação seria adicionado se você suspeitar que o valor de uma das variáveis de entrada altera a forma como uma variável de entrada diferente afeta a variável de saída.
Por exemplo, talvez para pessoas com crianças presentes durante uma estadia em um hotel, os jovens estejam mais satisfeitos do que os idosos, mas para pessoas sem crianças presentes, os jovens estão menos satisfeitos. Isso significaria que há uma interação entre “Children Present” (Crianças presentes) e “Age” (Idade)
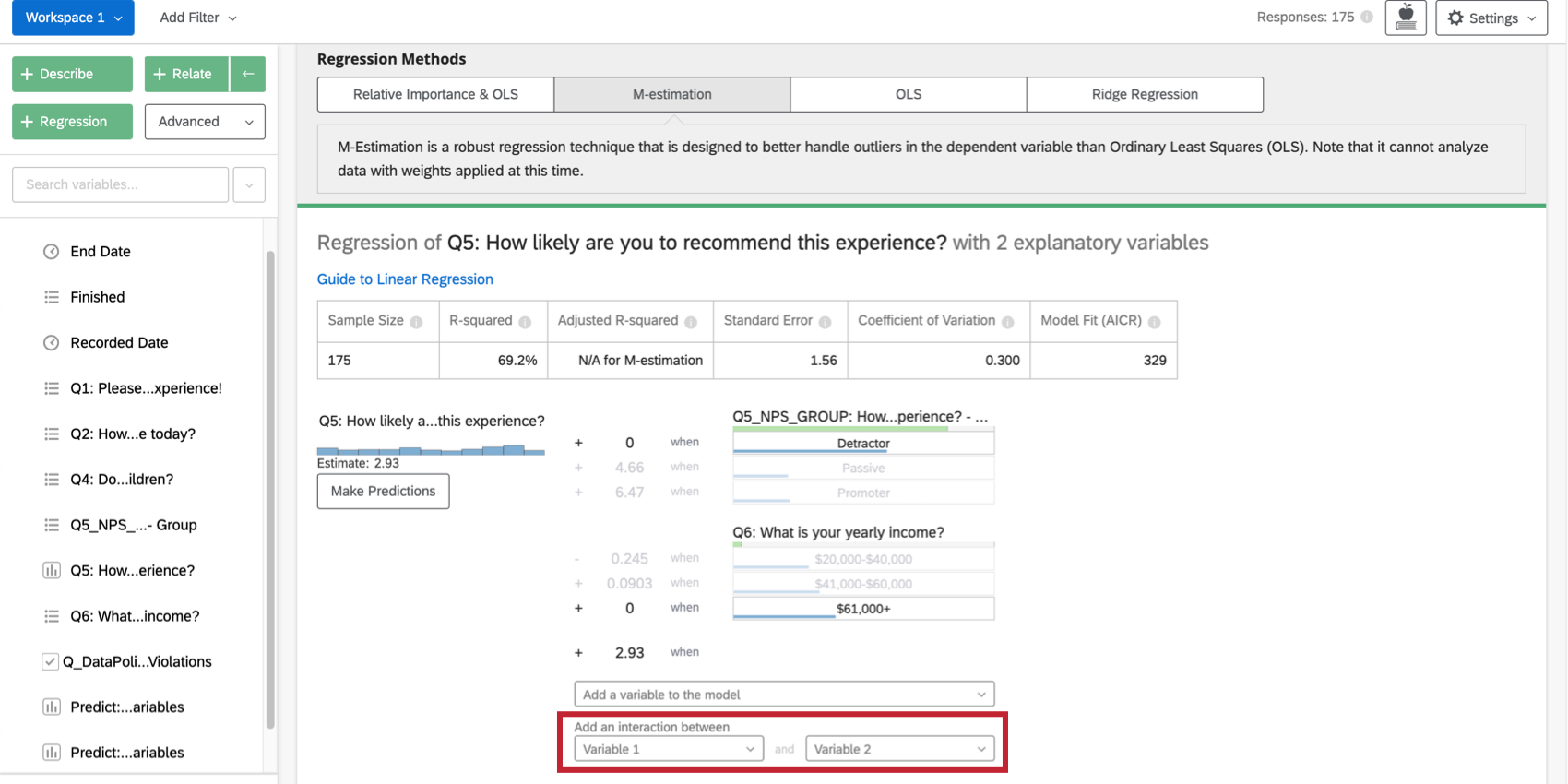
A seleção de duas variáveis em Adicionar uma interação entre, na parte inferior da lista de variáveis de entrada no cartão, adicionará um termo de interação à regressão. Essa funcionalidade só está disponível em Mínimos quadrados ordinários, M-Estimation e Ridge Regression.
É possível obter o mesmo efeito para variáveis categóricas em uma análise de importância relativa criando uma nova variável que combine as duas. Por exemplo, você pode combinar a variável Color (com grupos vermelho e verde ) com Size (com grupos grande e pequeno ) para criar uma variável chamada ColorSize (com grupos BigRed, BigGreen, SmallRed e SmallGreen).
Multicolinearidade
A multicolinearidade ocorre em um contexto de regressão quando duas ou mais das variáveis de entrada estão altamente correlacionadas entre si.
Quando duas variáveis são altamente correlacionadas, a matemática da regressão geralmente atribui o máximo de valor possível a uma variável e não à outra. Isso se manifesta em um coeficiente maior para essa variável. Porém, se o modelo for alterado, mesmo que ligeiramente (adicionando um filtro, por exemplo), a variável em que a maior parte do valor foi colocada pode mudar. Isso significa que mesmo uma pequena alteração pode ter um efeito drástico no modelo de regressão.
A análise de importância relativa lida com esse problema para que você não tenha que se preocupar com isso. Se você preferir usar um dos outros métodos e seu modelo apresentar esse problema, a presença de multicolinearidade (medida pelo “Variance Inflation Factor”) acionador um aviso e sugerirá que você remova uma variável ou combine variáveis calculando a média delas, por exemplo.
Mensagens de aviso
Stats iQ o avisará quando houver possíveis problemas com os resultados da regressão. Isso inclui as seguintes situações:
- As variáveis de entrada em sua regressão não são estatisticamente significativas.
- Sua transformação removeu dados da regressão.
- Duas ou mais variáveis estão altamente correlacionadas entre si e estão tornando seus resultados instáveis, ou seja, multicolinearidade.
- Os resíduos têm um padrão que sugere que o modelo pode ser aprimorado.
- Uma variável com apenas um valor foi removida automaticamente.
- O tamanho amostra é muito baixo em relação ao número de variáveis de entrada na regressão.
- Foi adicionada uma variável de categorias com muitas opções de resposta.