Guia fácil de usar para regressão logística

O que é Regressão logística?

A regressão logística estima uma fórmula matemática que relaciona uma ou mais variáveis de entrada a uma variável de saída.

Por exemplo, digamos que você administre um estande de limonada e esteja interessado em quais tipos de clientes tendem a voltar. Seus dados incluem uma entrada para cada cliente, sua primeira compra e se eles voltaram no mês seguinte para mais limonada. Seus dados podem ter o seguinte aspecto:

Você acha que “Idade do cliente” (uma variável de entrada ou explicativa) pode afetar “Retorno” (uma variável de saída ou de resposta). A regressão logística pode produzir este resultado:

Aos 12 anos (a idade mais baixa), a probabilidade de o retorno ser “Devolvido” é de 10%.

Para cada ano adicional de idade, “Return” é 1,1 vezes mais para ser “Devolvido”.

Este pouco de conhecimento é útil por duas razões.

Primeiro, ele permite que você entenda um relacionamento: clientes mais velhos têm maior probabilidade de retornar. Esse insight pode levá-lo a dobrar sua publicidade para clientes mais antigos, uma vez que eles serão mais propensos a se tornarem clientes repetidos.

Em segundo lugar, e relacionado, ele também pode ajudar você a fazer previsões específicas. Se um cliente de 24 anos passa, você pode estimar que, se ele comprou uma limonada, há uma chance de 26% de que, mais tarde, ele se torne um cliente de devolução.

Compreendendo a multiplicação de chances

Observe que se dissemos “Devolvido” era “1,5 vezes mais provável” em alguma situação do que em outra, estamos fazendo o seguinte:

Odds foram 1:9, também escrito 1/(1+9) = 10%.

As “chances para” (o 1) são multiplicadas por 1,5.

Agora 1.5:9, também escrito 1,5/(1.5+9) = 14%.

Outro exemplo é que, desta vez, de 50% de probabilidade para algo 3 vezes mais provável:

Odds foram 1:1, também escrito 1/(1+1) = 50%.

As “chances para” (o lado esquerdo 1) são multiplicadas por 3.

Agora 3:1, também escrito 3/(3+1) = 75%.

Agora vamos percorrer o processo de criação desse modelo de regressão.

Preparando para criar um modelo de regressão

1. Pense na teoria de sua regressão.

Depois de escolher uma variável de resposta, “Receita” hipotetiza como várias entradas podem estar relacionadas a ela. Por exemplo, você pode pensar que maior “Temperatura na primeira compra” levará a uma maior probabilidade de “Devolvido”, você pode não ter certeza de como “Age” afetará “Return“, e você pode acreditar que “Pants” (vs. shorts) é afetado pela “Temperatura”, mas não tem nenhum impacto em sua posição de limonada.

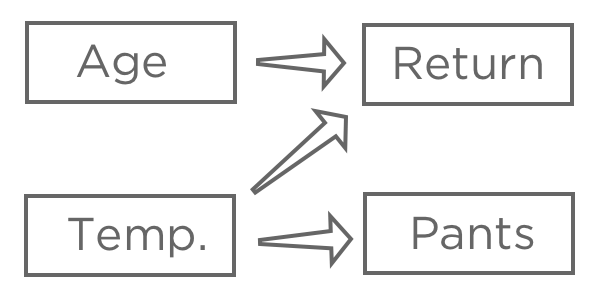
O objetivo da regressão é normalmente entender a relação entre várias entradas e uma saída, então, neste caso, você provavelmente decidiria criar um modelo explicando “Retorno” com “Temperatura” e “Idade” (também dito como “prever Retorno da Temperatura e da Idade”, mesmo que você esteja mais interessado em explicação do que a previsão real).

Você provavelmente não incluiria “Calça” em sua regressão. Ele pode estar correlacionado com “Retorno” porque ambos estão relacionados com “Temperatura”, mas não vem antes de “Retorno” na cadeia causal, então, incluindo isso confundiria seu modelo.

2. “Descreva” todas as variáveis que podem ser úteis para seu modelo.

Comece descrevendo a variável resposta, neste caso “Receita”, e sinta-se bem por ela. Faça o mesmo para suas variáveis explicativas.

Observe que têm uma forma como esta…

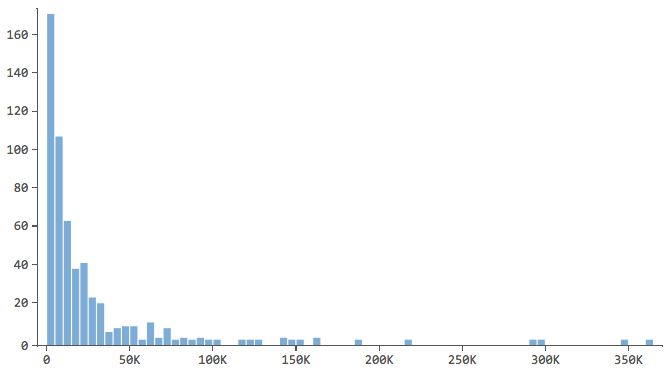
…onde a maioria dos dados está nas primeiras lixeiras do histograma. Essas variáveis exigirão atenção especial posteriormente.

3. “Relacionar” todas as variáveis explicativas possíveis com a variável de resposta.

O Stats iQ ordenará os resultados pela força da relação estatística. Dê uma olhada e sinta os resultados, observando quais variáveis estão relacionadas à “Receita” e como.

4. Comece a construir a regressão.

A construção de um modelo de regressão é um processo iterativo. Você percorrerá as três fases a seguir quantas vezes forem necessárias.

Os três estágios da construção de um modelo de regressão

Fase 1: adicionar ou subtrair uma variável.

Uma a uma, comece a adicionar variáveis que suas análises anteriores indicaram estarem relacionadas a “Receita” (ou adicione variáveis que você tem um motivo teórico para adicionar). Ir um por um não é estritamente necessário, mas facilita a identificação e a correção de problemas à medida que você avança e ajuda você a obter uma sensação para o modelo.

Digamos que você comece prevendo “Receita” com “Temperatura”. Você encontra uma relação forte, avalia o modelo e acha que é satisfatório (mais detalhes em um minuto).

Temperatura da devolução

Em seguida, você adiciona “Cor da Lemonade” e agora seu modelo de regressão tem dois termos, ambos estatisticamente significativos. Assim:

Receita <– Cor da temperatura e da Lemonade

Em seguida, você adiciona “Sexo”, e os resultados do modelo agora mostram que “Sexo” é estatisticamente significativo no modelo, mas a “Cor da Lemonade” não é mais. Normalmente, você removeria a “cor da Lemonade” do modelo. Agora temos:

Receita <– Temperatura e sexo

Ou seja, se você sabe o sexo do cliente, saber que cor de limonada ele pediu não dá mais informações sobre se será um cliente de devolução.

Você pode investigar e descobrir que as mulheres tendem a escolher a limonada amarela mais do que os homens e que as mulheres são mais propensas a retornar. Então, inicialmente parecia que a escolha do amarelo tornou um cliente mais propenso a retornar, mas, de fato, “Lemonade color” só está relacionado com “Return” através de “Sex“. Assim, quando você inclui “Sex” na regressão, “Lemonade color” desce da regressão.

Interpretar os resultados da regressão faz bom senso e, só porque uma variável é estatisticamente significativa, não significa que ela seja realmente causal. Mas adicionando e subtraindo cuidadosamente variáveis, observando como o modelo muda e sempre pensando na teoria por trás de seu modelo, você pode separar relações interessantes em seus dados.

Etapa 2: Avaliar o modelo.

Sempre que você adicionar ou subtrair uma variável, você deve avaliar a precisão do modelo observando seu coeficiente de determinação (^R2), AICc e quaisquer alertas do Stats iQ. Sempre que você modificar o modelo, compare os novos gráficos de coeficiente de determinação, AICc e diagnóstico com os antigos para determinar se o modelo melhorou ou não.

Coeficiente de determinação (^R2)

A métrica numérica para quantificar a precisão da previsão do modelo é conhecida como coeficiente de determinação, que fica entre zero e um. Um zero significa que o modelo não tem valor preditivo e um significa que o modelo prevê tudo perfeitamente.

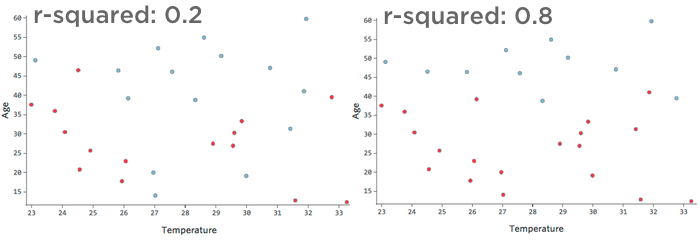
Por exemplo, os dados representados à esquerda levarão a um modelo muito menos preciso do que os dados à direita. Imagine tentar desenhar uma linha através do gráfico de dispersão; você poderia quase completamente separar o azul (“Devolvido”) do vermelho (“Não”) no lado direito, mas no lado esquerdo seria difícil fazê-lo.

Ou seja, o lado direito tem um alto coeficiente de determinação; se você sabe “Temperatura” e “Idade”, você pode determinar “Devolvido” vs. “Não” muito facilmente. O lado esquerdo tem um coeficiente de determinação baixo a médio; se você sabe “Temperatura” e “Idade”, você tem um palpite muito bom sobre se ele será “Devolvido” vs. “Não”, mas haverá muitos erros.

Não existe uma definição fixa de um coeficiente de determinação “bom”. Em algumas configurações, pode ser interessante ver qualquer efeito, enquanto em outras seu modelo pode ser inútil, a menos que seja altamente preciso.

Sempre que você adicionar uma variável, o coeficiente de determinação aumentará, portanto alcançar o maior coeficiente de determinação possível não é o objetivo; em vez disso, você quer equilibrar a precisão do modelo (coeficiente de determinação) com sua complexidade (geralmente, o número de variáveis nele).

AICc

A AICc é uma métrica que equilibra a precisão com complexidade – maior precisão leva a melhores pontuações e adiciona complexidade (mais variáveis) leva a piores pontuações. O modelo com o AICc inferior é melhor.

Observe que a métrica AICc só é útil para comparar AICcs de modelos que têm o mesmo número de linhas de dados e a mesma variável de saída.

Alertas

De tempos em tempos, o Stats iQ sugerirá maneiras de melhorar seu modelo. Por exemplo, o Stats iQ pode sugerir que você pegue o logaritmo de uma variável (detalhes sobre o que isso significa).

Matriz de confusão e curva de recuperação de precisão

A matriz de confusão e a curva de recolha de precisão também são ferramentas úteis para entender a precisão do seu modelo. E se você quiser fazer previsões com base em seu modelo, essas ferramentas o ajudarão a fazer isso. Eles não são estritamente necessários para entender bem o que seu modelo está dizendo, por isso os colocamos em uma seção diferente sobre a matriz de confusão e a curva de recordação de precisão

Estágio 3: Modifique o modelo de acordo.

Se a sua avaliação do modelo tiver sido satisfatória, você concluiu ou pode voltar para a Fase 1 e inserir mais variáveis.

Se sua avaliação encontrar o modelo faltando, você usará os alertas do Stats iQ para corrigir os problemas.

Conforme você modifica o modelo, observe continuamente o coeficiente de determinação de modificações, a AICR e os diagnósticos residuais e decida se as modificações que você está efetuando estão ajudando ou prejudicando seu modelo.

Perguntas frequentes