Guia fácil de usar para regressão linear

O que é regressão?

A regressão estima uma fórmula matemática que relaciona uma ou mais variáveis de entrada a uma variável de saída.

Por exemplo, digamos que você administre um estande de limonada e esteja interessado no que gera receita. Seus dados incluem “Receita” de cada dia, alta “Temperatura”, “Número de crianças que andaram por”, “Número de adultos que andaram”, que “Sinalização” você usou naquele dia e uma “Receita do concorrente” nas proximidades.

Você acha que “Temperatura” (uma variável de entrada ou explicativa) pode afetar “Receita” (uma variável de saída ou resposta). Quando você usa regressão para analisar essa relação, isso pode resultar nesta fórmula:

Receita = 2,71 * Temperatura   –   35Esta

fórmula é útil por dois motivos.

Primeiro, permite que você entenda um relacionamento: dias mais quentes levam a mais “Receita”. Em particular, o 2,71 antes de “Temperatura” (chamado de coeficiente) significa que para cada grau “Temperatura” sobe, em média, haverá US$ 2,71 a mais “Receita”. Esse insight pode levá-lo a decidir não vender limonada em dias frios.

Em segundo lugar, e relacionado, ele também pode ajudar você a fazer previsões específicas. Se a “Temperatura” for 24, você poderia estimar que desde…

Receita = 2,71 * Temperatura   –   35
Receita = 2,71 * 24   –   35
Receita = 30

…você terá cerca de US$ 30 em “Receita”. Essas podem ser informações úteis para saber se você conseguirá fazer um pagamento nesse dia, assumindo que está confiante de que seu modelo é preciso.

Agora vamos percorrer o processo de criação dessa equação de regressão.

Preparando para criar um modelo de regressão

1. Pense na teoria de sua regressão

Depois de escolher uma variável de resposta, “Receita“, hipotetizar como várias entradas podem estar relacionadas a ela. Por exemplo, você pode pensar que a “Temperatura” mais alta levará a uma “Receita” mais alta, você pode não ter certeza de como várias sinalizações afetarão a “Receita“, e pode acreditar que as “Vendas do concorrente” são afetadas pela “Temperatura”, mas não têm impacto em seu estande de limonada.

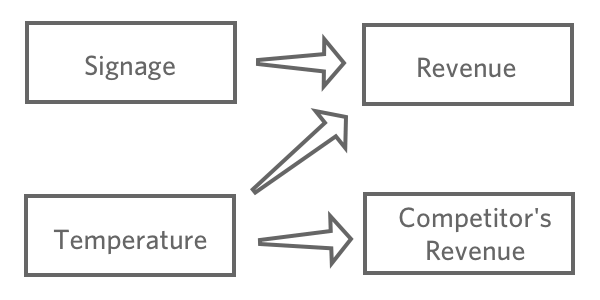
O objetivo da regressão é normalmente entender a relação entre várias entradas e uma saída, por isso, neste caso, você provavelmente decidiria criar um modelo explicando “Receita” com “Temperatura” e “Sinalização” (também dito como “previsão de receita da temperatura e sinalização“, mesmo que você esteja mais interessado na explicação do que na previsão real).

Você provavelmente não incluiria “Vendas do concorrente” em sua regressão. É provável que esteja correlacionado com “Receita”, mas não vem antes dela na cadeia causal, então incluindo isso confundiria seu modelo.

2. “Descreva” todas as variáveis que podem ser úteis para seu modelo

Comece descrevendo a variável de resposta, neste caso “Receita”, e obtendo uma boa sensação para ela. Faça o mesmo para suas variáveis explicativas.

Observe que têm uma forma como esta…

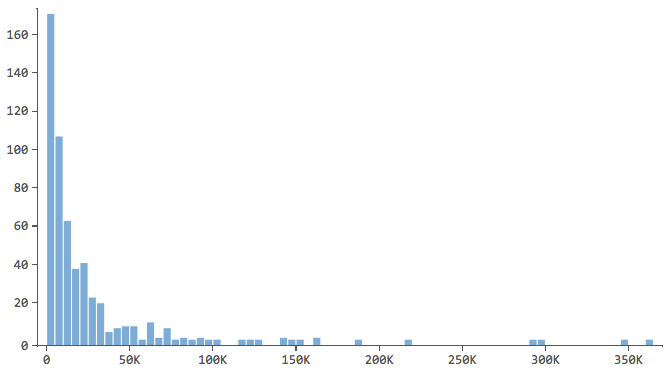
…onde a maioria dos dados está nas primeiras lixeiras do histograma. Essas variáveis exigirão atenção especial posteriormente.

3. “Relacionar” todas as variáveis explicativas possíveis com a variável de resposta

O Stats iQ ordenará os resultados pela força da relação estatística. Dê uma olhada e sinta os resultados, observando quais variáveis estão relacionadas à “Receita” e como.

Se você já tiver uma boa ideia de quais variáveis devem conduzir teoricamente a saída (por exemplo, de trabalhos acadêmicos anteriores), você deve ignorar esta etapa. Mas se sua análise for um pouco mais exploratória (como uma pesquisa de cliente), esta é uma etapa útil e importante.

4. Iniciar a construção da regressão

A construção de um modelo de regressão é um processo iterativo. Você percorrerá as três fases a seguir quantas vezes forem necessárias.

Os três estágios da construção de um modelo de regressão

Fase 1: adicionar ou subtrair uma variável

Uma a uma, comece a adicionar variáveis que suas análises anteriores indicaram estarem relacionadas a “Receita” (ou adicione variáveis que você tem um motivo teórico para adicionar). Ir um por um não é estritamente necessário, mas facilita a identificação e a correção de problemas à medida que você avança e ajuda você a obter uma sensação para o modelo.

Digamos que você comece prevendo “Receita” com “Temperatura”. Você encontra uma relação forte, avalia o modelo e acha que é satisfatório (mais detalhes em um minuto).

Receita = 2,71 * Temperatura   –   35Você

adiciona então “Número de crianças que passaram” e agora seu modelo de regressão tem dois termos, ambos preditores estatisticamente significativos. Assim:

Receita = 2,5 * Temperatura   +   0.3 * NumberOfChildrenWhoWalkedBy   –   12Então

você adiciona “Número de adultos que caminharam”, e os resultados do modelo agora mostram que “Número de adultos” é estatisticamente significativo no modelo, mas “Número de crianças” não é mais. Normalmente, você removeria “Número de filhos” do modelo. Agora temos:

Receita = 2,6 * Temperatura   +   0.4 * NumberOfAdultsWhoWalkedBy   –   14

Isso significa que “Número de adultos” é o melhor preditor de “Receita”; ou seja, se você souber quantos adultos chegam, saber em quantas crianças chegam não adiciona nenhuma informação nova – isso não o ajuda a prever vendas.

Talvez você pense e lembre-se de que as crianças realmente não compram sua limonada, por isso faz sentido que essa variável não pertença ao modelo.

Mas por que ela foi estatisticamente significativa no primeiro modelo? Provavelmente porque “Número de crianças” está correlacionado com “Número de adultos“, e como “Número de adultos” ainda não estava no modelo, “Número de crianças” estava agindo como uma proxy grosseira para “Número de adultos”.

Interpretar os resultados da regressão faz muito sentido e só porque uma variável é estatisticamente significativa não significa que ela seja realmente causal. Mas adicionando e subtraindo cuidadosamente variáveis, observando como o modelo muda e sempre pensando na teoria por trás de seu modelo, você pode separar relações interessantes em seus dados.

Etapa 2: Avaliar o modelo

Toda vez que você adicionar ou subtrair uma variável, você deve avaliar a precisão do modelo observando seu coeficiente de determinação (^R2), AICR, e seus gráficos residuais. Sempre que você modificar o modelo, compare os novos gráficos de coeficiente de determinação, AICR e residual com os antigos para determinar se o modelo melhorou ou não.

Coeficiente de determinação (^R2)

A métrica numérica para quantificar a precisão da previsão do modelo é conhecida como coeficiente de determinação, que fica entre zero e um. Um zero significa que o modelo não tem valor preditivo e um significa que o modelo prevê tudo perfeitamente.

Por exemplo, o modelo à esquerda é mais preciso do que o da direita; ou seja, se você sabe “Temperatura”, você tem um palpite muito bom sobre o que “Receita” estará à esquerda, mas não realmente à direita.

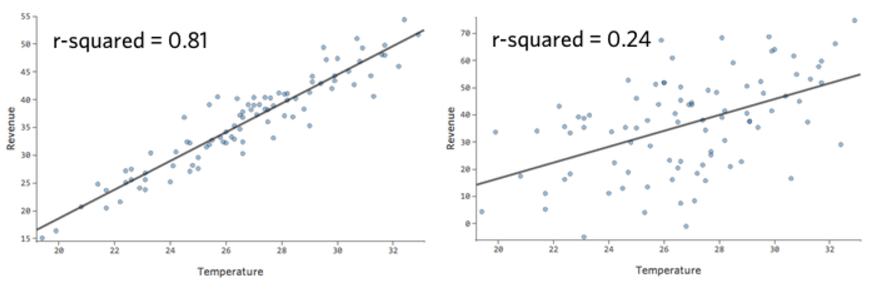
Não existe uma definição fixa de um coeficiente de determinação “bom”. Em algumas configurações, pode ser interessante ver qualquer efeito, enquanto em outras seu modelo pode ser inútil, a menos que seja altamente preciso.

Sempre que você adicionar uma variável, o coeficiente de determinação aumentará, portanto alcançar o maior coeficiente de determinação possível não é o objetivo; em vez disso, você quer equilibrar a precisão do modelo (coeficiente de determinação) com sua complexidade (geralmente, o número de variáveis nele).

AICR

A AICR é uma métrica que equilibra a precisão com complexidade – maior precisão leva a melhores pontuações, maior complexidade (mais variáveis) leva a pontuações piores. O modelo com a menor AICR é melhor.

Observe que a métrica AICR só é útil para comparar AICRs de modelos que têm o mesmo número de linhas de dados ea mesma variável de saída.

Intervalos de previsão

Outra forma útil de obter uma sensação de precisão do seu modelo é manter os valores de amostra em sua fórmula e ver o intervalo de previsão calculado pelo Stats iQ. Por exemplo, se você colocar o número 30 na fórmula, o Stats iQ informará que o valor previsto é 45,5, mas o intervalo de confiança de 95% é 36,4 a 54,5, o que significa que você pode ter 95% de certeza de que, se amanhã vier a ser 30 graus, você obteria entre US$ 36,40 e US$ 54,50 em “Receita”. Você poderia imaginar um modelo mais preciso onde o intervalo de previsão era uma banda apertada como $44 a $48, ou um menos preciso onde o intervalo era amplo, como $20 a $72.

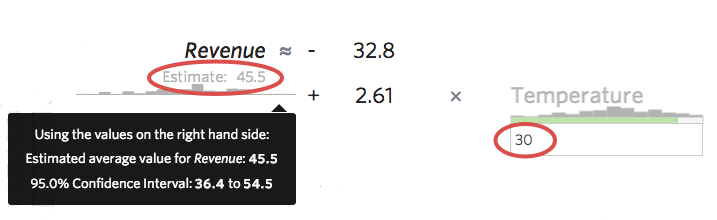
Essa abordagem só é útil quando seus gráficos residuais parecem saudáveis (veja abaixo), caso contrário, eles serão imprecisos.

Residuais

Os resíduos são a principal ferramenta de diagnóstico para avaliar e melhorar a regressão, por isso há uma seção separada inteira sobre a interpretação de resíduos para melhorar seu modelo. Você aprenderá ou atualizará sua memória sobre o que são resíduos, como usá-los para avaliar e melhorar o modelo e como pensar na precisão do seu modelo.

Recomendamos que você a leia na íntegra, pois ela abrangerá tudo o que você precisa para produzir um ótimo modelo. Mas você sempre pode voltar a isso, é claro.

Etapa 3: modificar o modelo de acordo

Se sua avaliação do modelo tiver considerado satisfatória, você concluiu ou pode voltar para a Fase 1 e inserir mais variáveis.

Se sua avaliação encontrar o modelo em falta, você usará os alertas do Stats iQ e a seção de diagnóstico residual para corrigir os problemas.

Conforme você modifica o modelo, observe continuamente o coeficiente de determinação de modificações, a AICR e os diagnósticos residuais e decida se as modificações que você está efetuando estão ajudando ou prejudicando seu modelo.

Perguntas frequentes