Interpretando parcelas residuais para melhorar sua regressão
Ao executar uma regressão, o Stats iQ calcula e parcela os resíduos automaticamente para ajudá-lo a entender e melhorar seu modelo de regressão. Leia abaixo para saber tudo o que você precisa descobrir sobre a interpretação de resíduos (incluindo definições e exemplos).
Observações, previsões e resíduos
Para demonstrar como interpretar resíduos, usaremos um conjunto de dados de barraquinha de limonada, onde cada linha representa um dia de “Temperatura” e “Receita”.
| Temperatura (Celsius) | Receita |
|---|---|
| 28,2 | US$ 44 |
| 21,4 | US$ 23 |
| 32,9 | US$ 43 |
| 24,0 | US$ 30 |
| etc. | etc. |
A equação de regressão que descreve a relação entre “Temperatura” e “Receita” é:
Receita = 2,7 * Temperatura – 35
Digamos que, um dia, a temperatura na barraquinha de limonada foi de 30,7 graus, e a “Receita” foi de US$ 50. US$ 50 é o resultado observado ou real , o valor que realmente aconteceu.
Então, se inserirmos 30,7 no nosso valor para “Temperatura”…
Receita = 2,7 * 30,7 – 35
Receita = 48
…obtemos US$ 48. Esse é o valor previsto para aquele dia, também conhecido como o valor para “Receita”, a equação de regressão teria previsto com base na “Temperatura”.
Seu modelo nem sempre está perfeitamente certo, é claro. Neste caso, a previsão é desativada por 2; essa diferença, a 2, é chamada de resíduo. O resíduo é o bit que resta quando você subtrai o valor previsto do valor observado.
Residual = Observado – Previsão
Você pode imaginar que cada linha de dados agora tem, além disso, um valor previsto e um residual.
| Temperatura (Celsius) |
Receita (observada) |
Receita (prevista) |
Residual (observado – previsto) |
|---|---|---|---|
| 28,2 | US$ 44 | US$ 41 | US$ 3 |
| 21,4 | US$ 23 | US$ 23 | US$ 0 |
| 32,9 | US$ 43 | US$ 54 | -US$ 11 |
| 24,0 | US$ 30 | US$ 29 | US$ 1 |
| etc. | etc. | etc. | etc. |
Vamos usar os valores observados, previstos e residuais para avaliar e melhorar o modelo.
Entendendo a precisão com Observado vs. Previsto
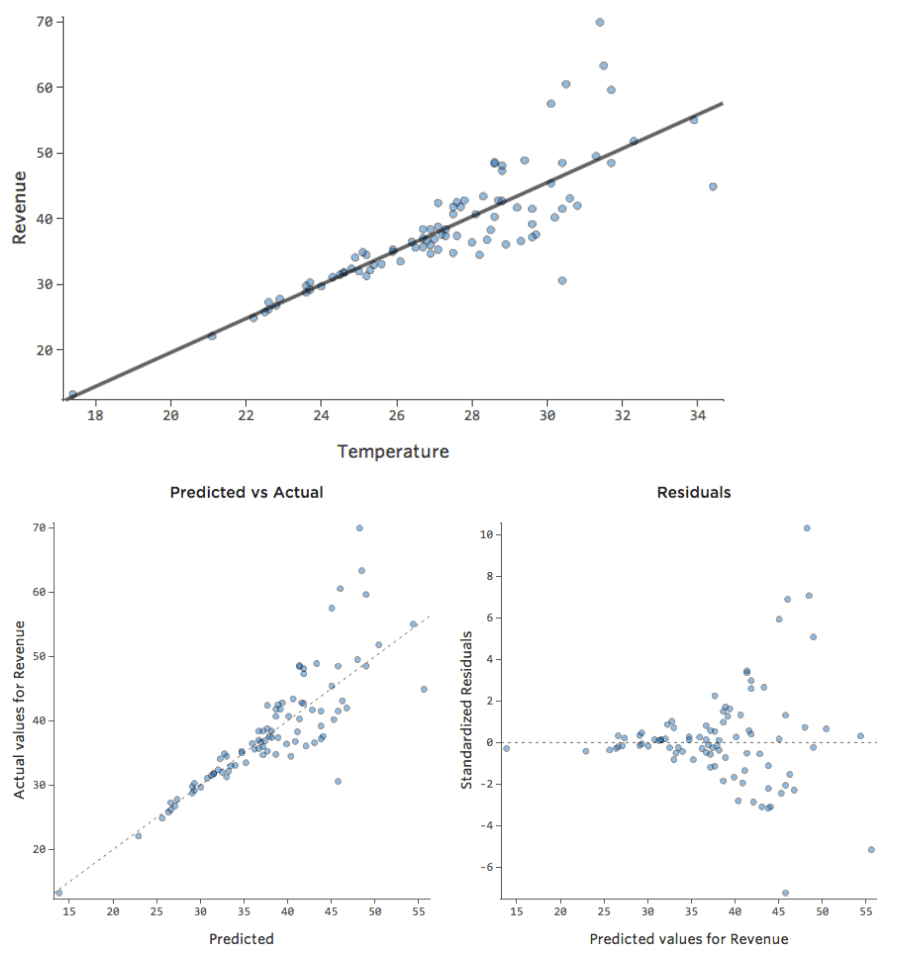
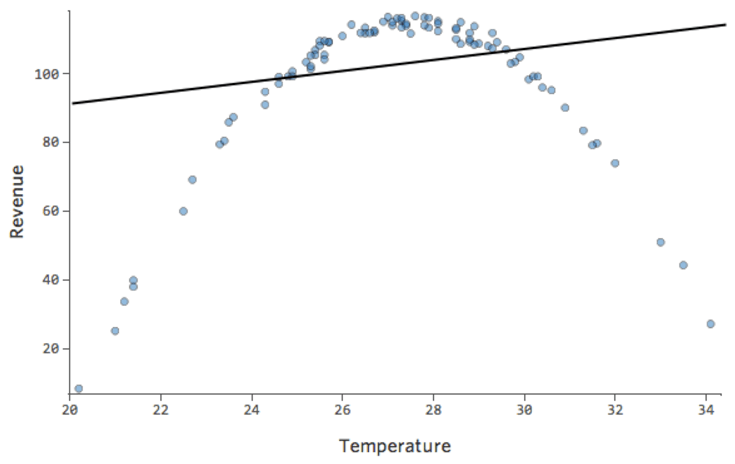
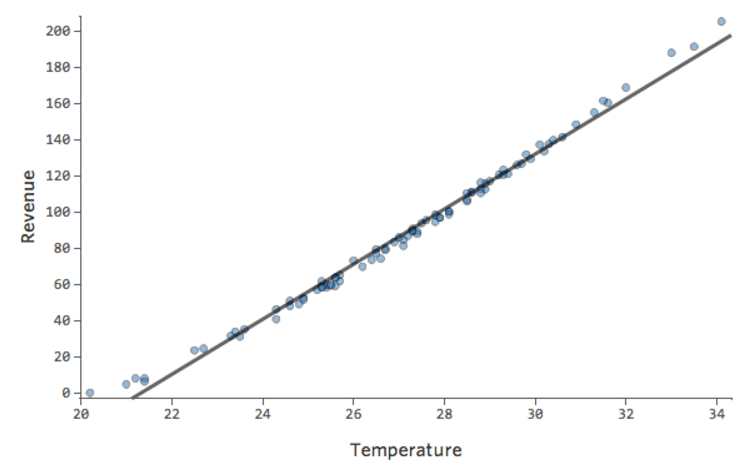
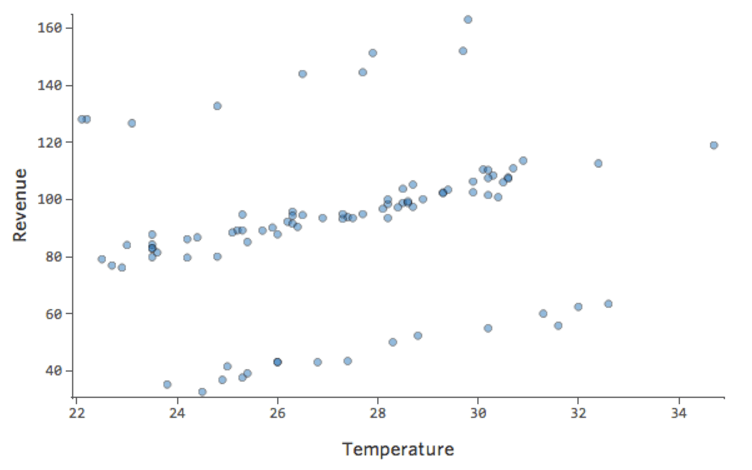
Em um modelo simples como este, com apenas duas variáveis, você pode ter uma noção da precisão do modelo apenas relacionando “Temperatura” a “Receita”. Aqui está a mesma execução de regressão em duas barracas de limonada diferentes, uma onde o modelo é muito preciso, outra onde o modelo não é:
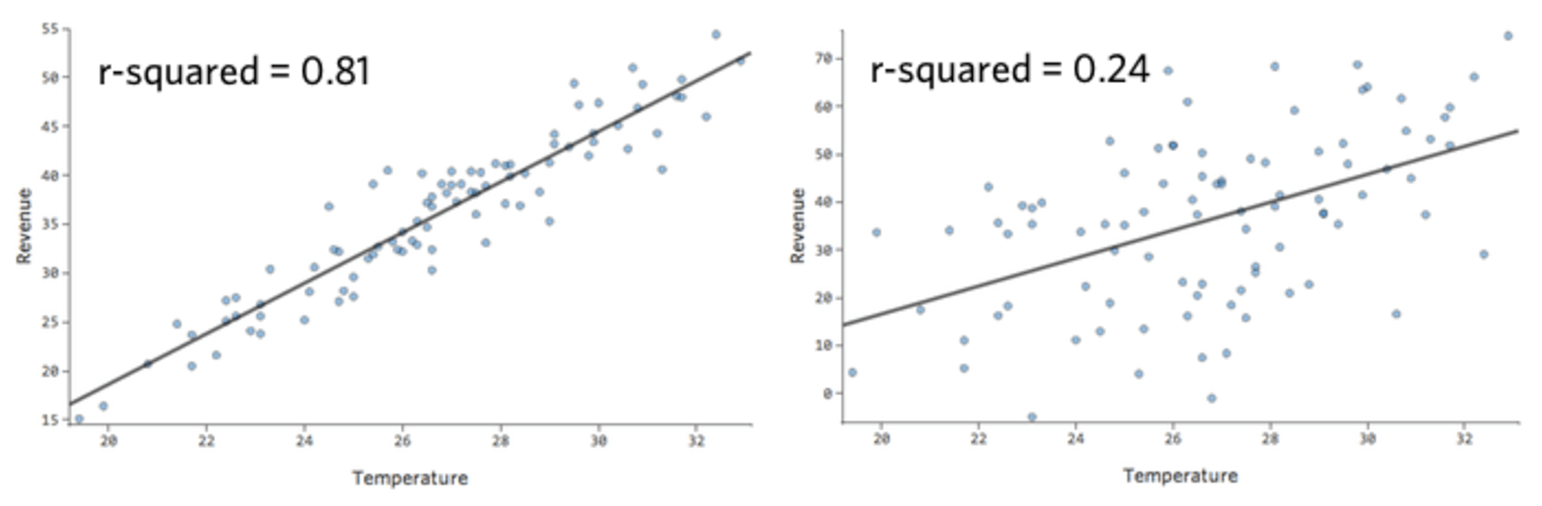
É claro que, para ambos as barracas de limonada, uma “Temperatura” mais alta está associada à maior “Receita”. Mas em uma dada “Temperatura”, você poderia prever que a “Receita” da barraca de limonada esquerda fica muito mais precisa do que a barraca de limonada direita, o que significa que o modelo é muito mais preciso.
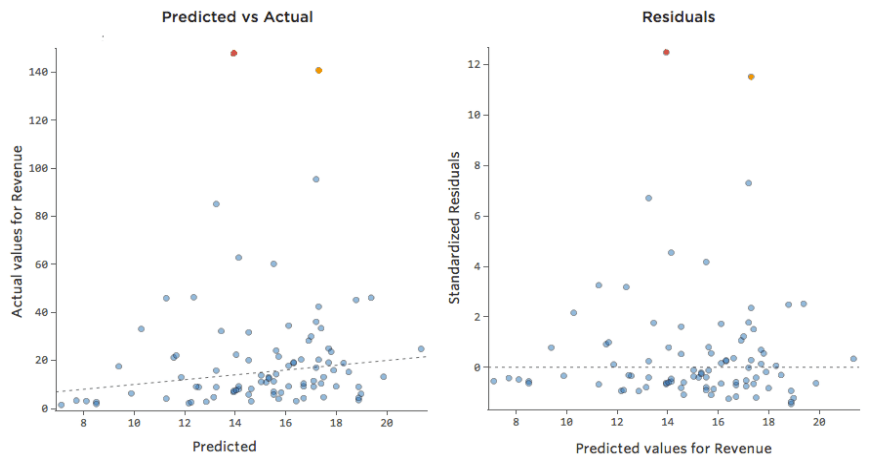
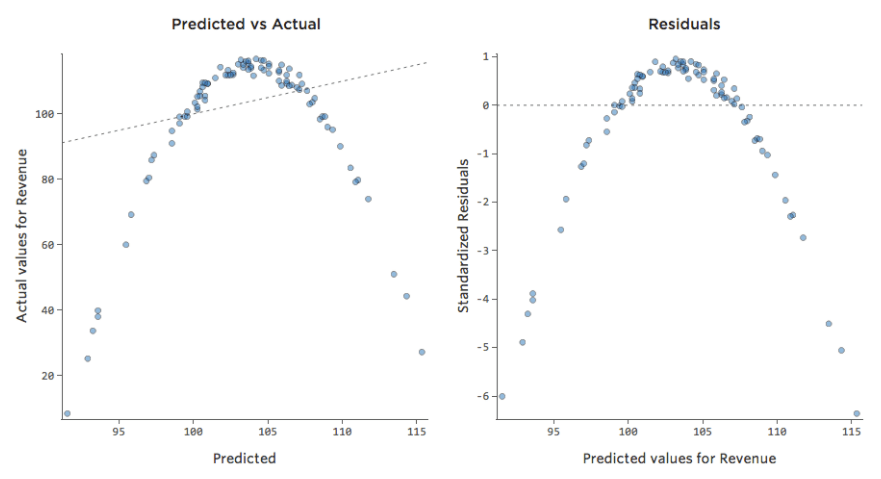
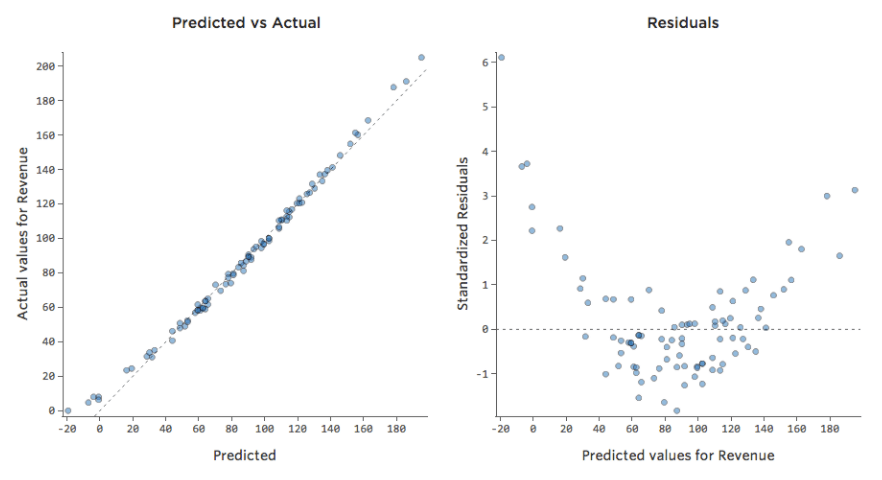
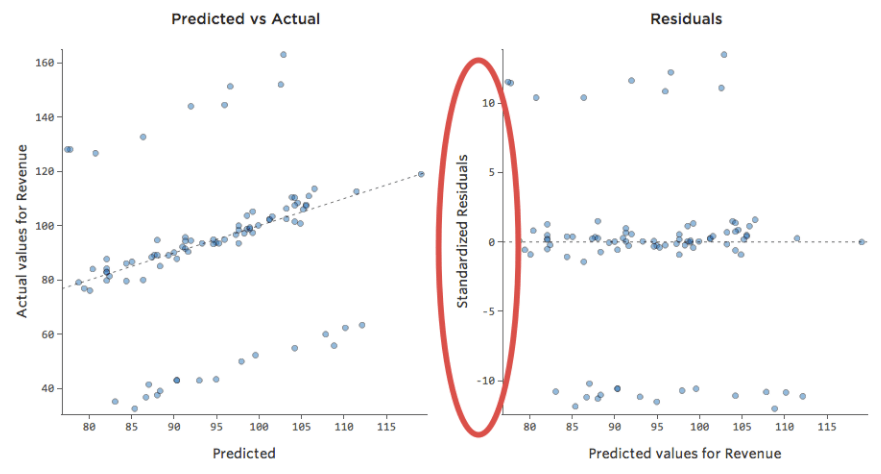
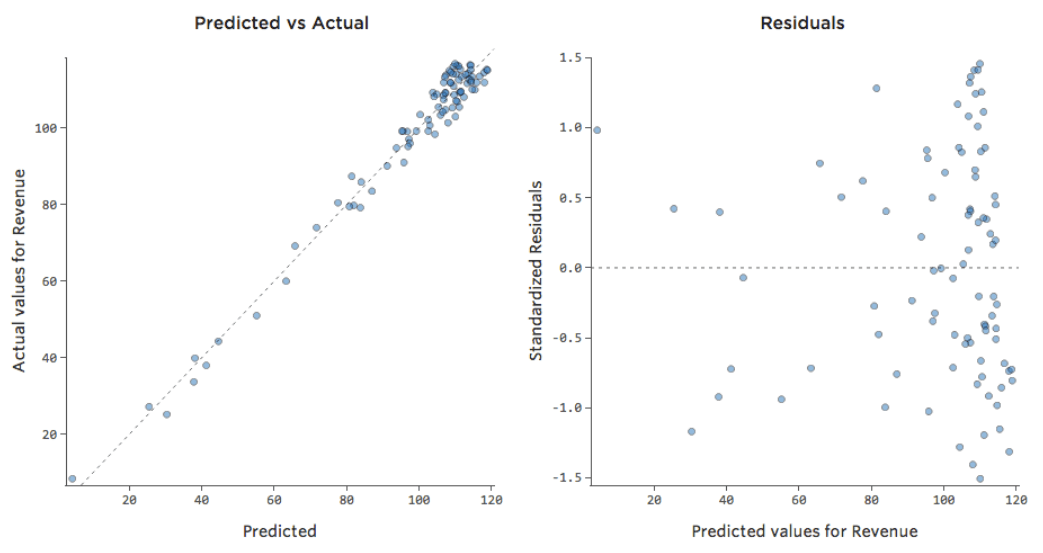
Mas a maioria dos modelos tem mais de uma variável explicativa e não é prático representar mais variáveis em um gráfico como esse. Em vez disso, vamos representar os valores previstos em relação aos valores observados para esses mesmos conjuntos de dados.
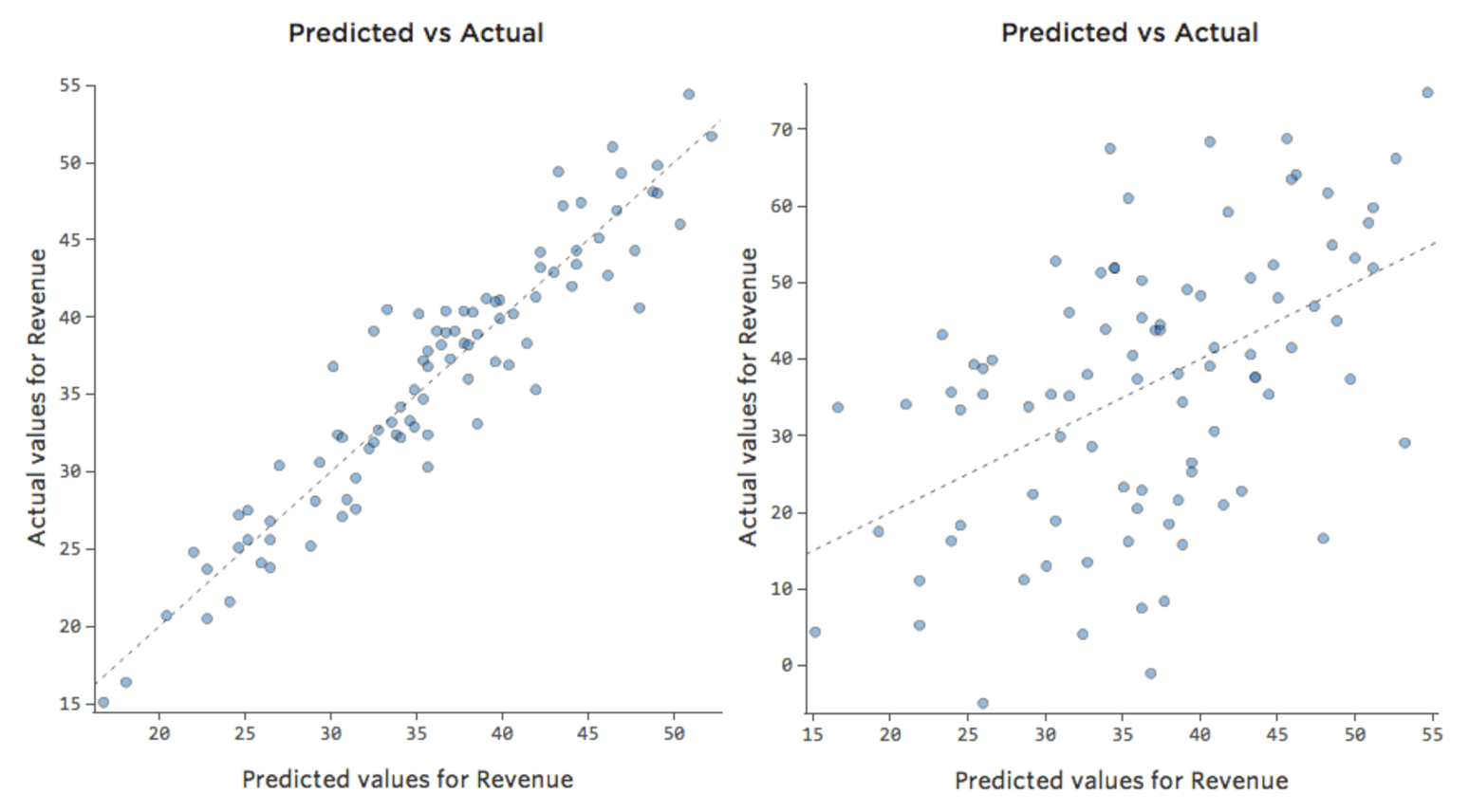
Novamente, o modelo para o gráfico à esquerda é muito preciso; há uma forte correlação entre as previsões do modelo e seus resultados reais. O modelo para o gráfico na extrema direita é o oposto; as previsões do modelo não são muito boas.
Observe que esses gráficos se parecem exatamente com a “Temperatura” vs. “Receita” acima deles, mas o eixo x é previsto “Receita” ao invés de “Temperatura“. Isso é comum quando sua equação de regressão só tem uma variável explicativa. No entanto, com mais frequência, você terá múltiplas variáveis explicativas, e esses gráficos terão uma aparência bem diferente de um diagrama de qualquer variável explicativa vs. “Receita.”
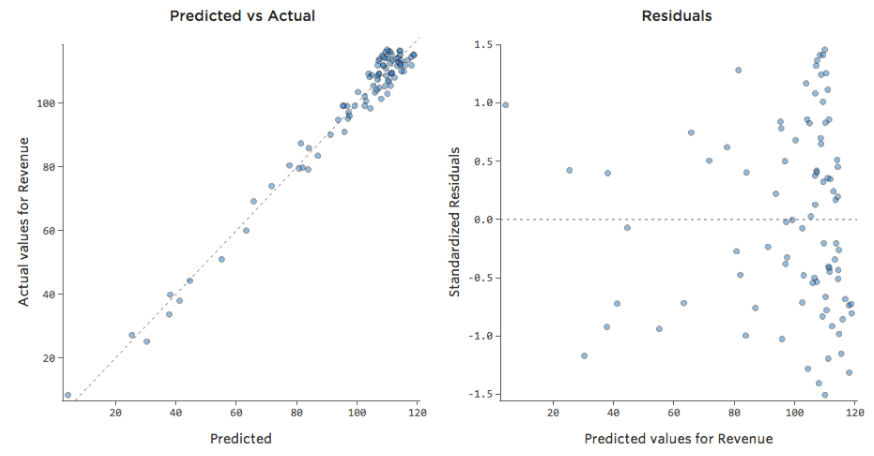
Examinando Previsto vs. Residual (“O lote residual”)
A forma mais útil de plotar os resíduos, no entanto, é com seus valores previstos no eixo x e seus resíduos no eixo y.
(O Stats iQ apresenta resíduos como resíduos padronizados, o que significa que cada gráfico residual que você observa com qualquer modelo está no mesmo eixo y padronizado.)
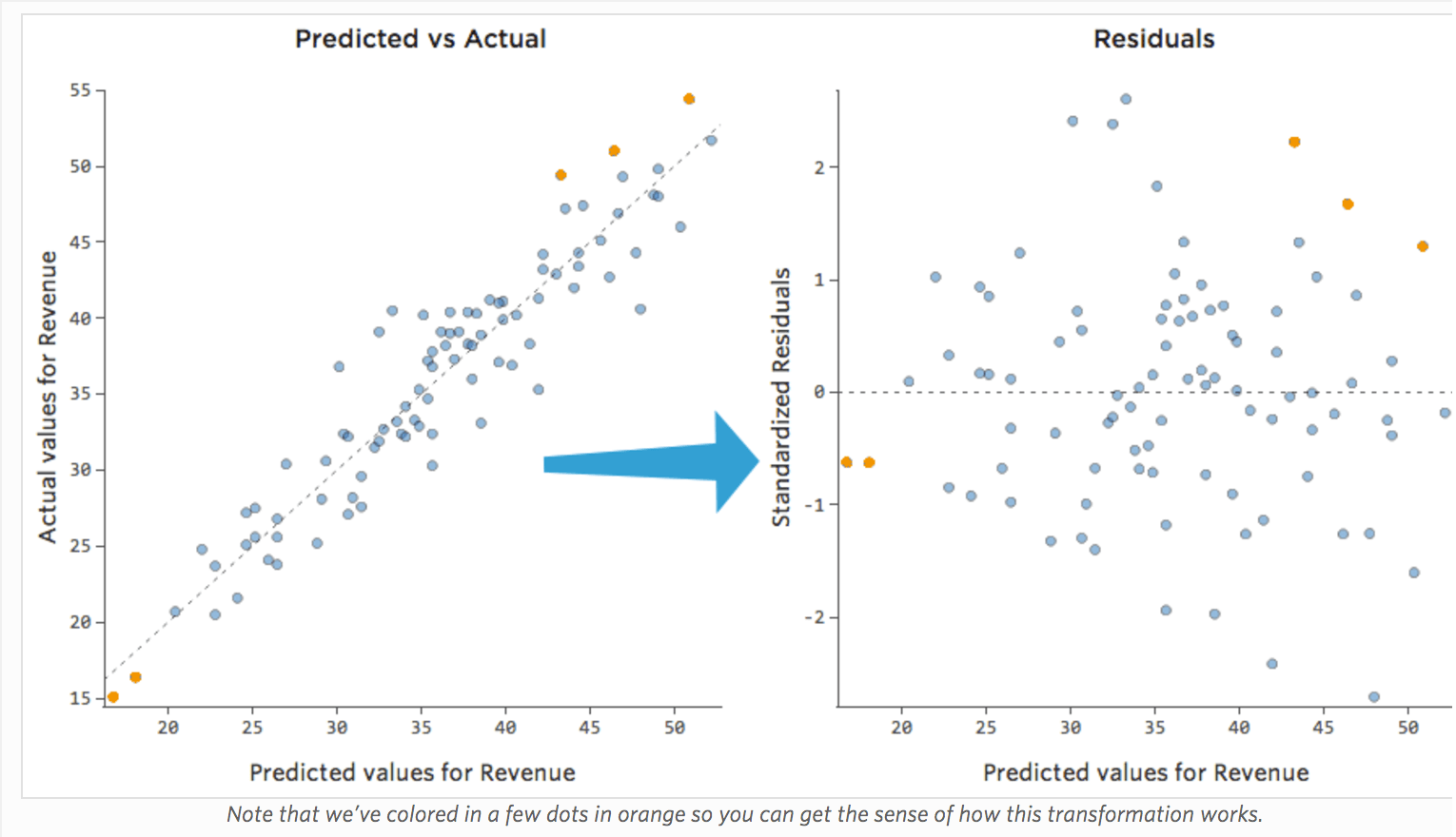
No gráfico à direita, cada ponto é um dia, onde a previsão feita pelo modelo está no eixo x e a precisão da previsão está no eixo y. A distância da linha em 0 é o quão ruim foi a previsão para esse valor.
Uma vez que…
Residual = Observado – Previsto
…valores positivos para o residual (no eixo y) significam que a previsão era muito baixa, e valores negativos significam que a previsão era muito alta; 0 significa que o palpite estava exatamente correto.
Idealmente, a sua representação dos resíduos tem o seguinte aspecto:
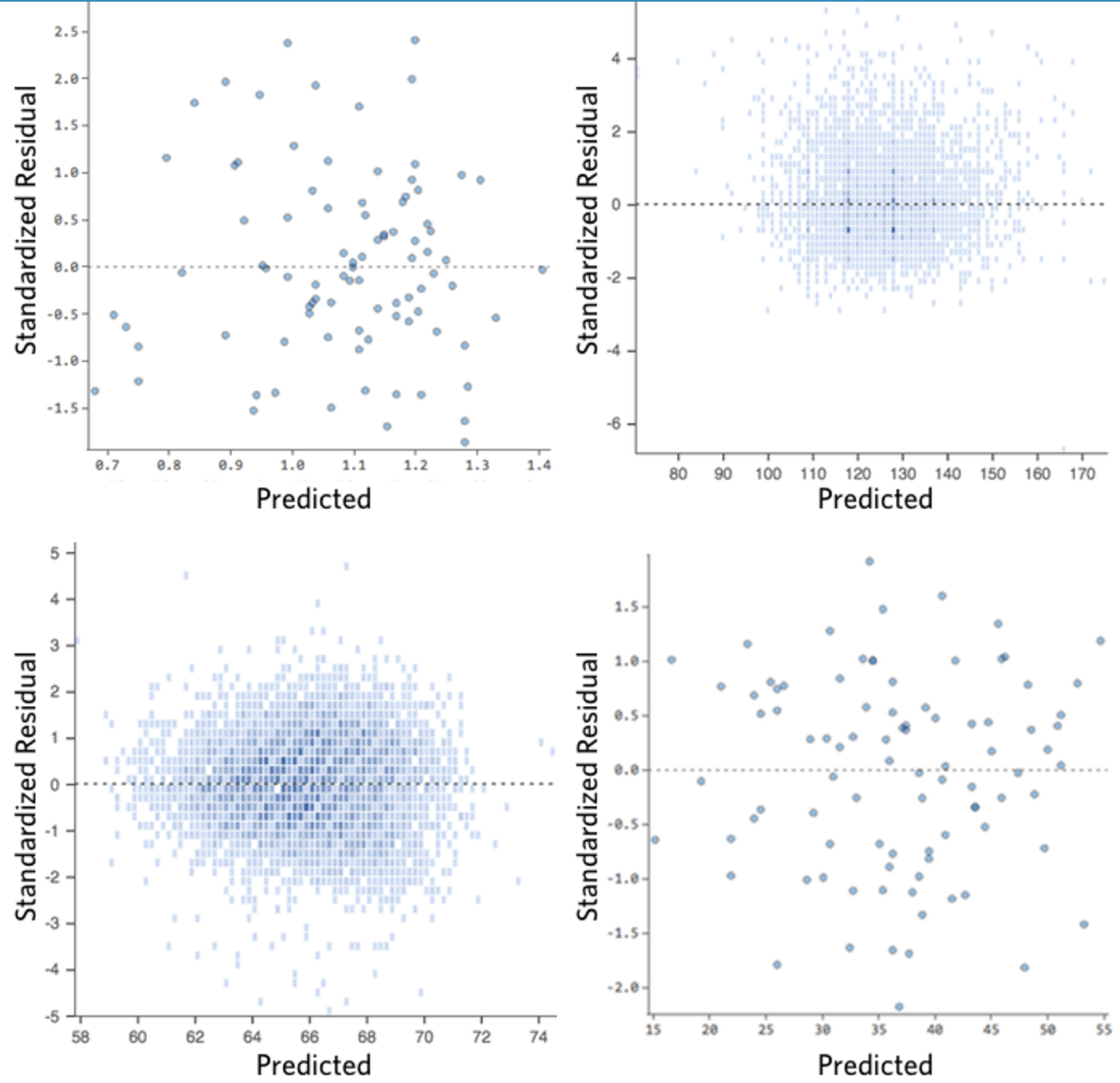
Ou seja,
(1) eles são bem distribuídos simetricamente, tendendo a se aglomerar no meio do gráfico.
(2) eles estão agrupados em torno dos dígitos individuais mais baixos do eixo y (por exemplo, 0,5 ou 1,5, não 30 ou 150).
(3) em geral, não há nenhum padrão claro.
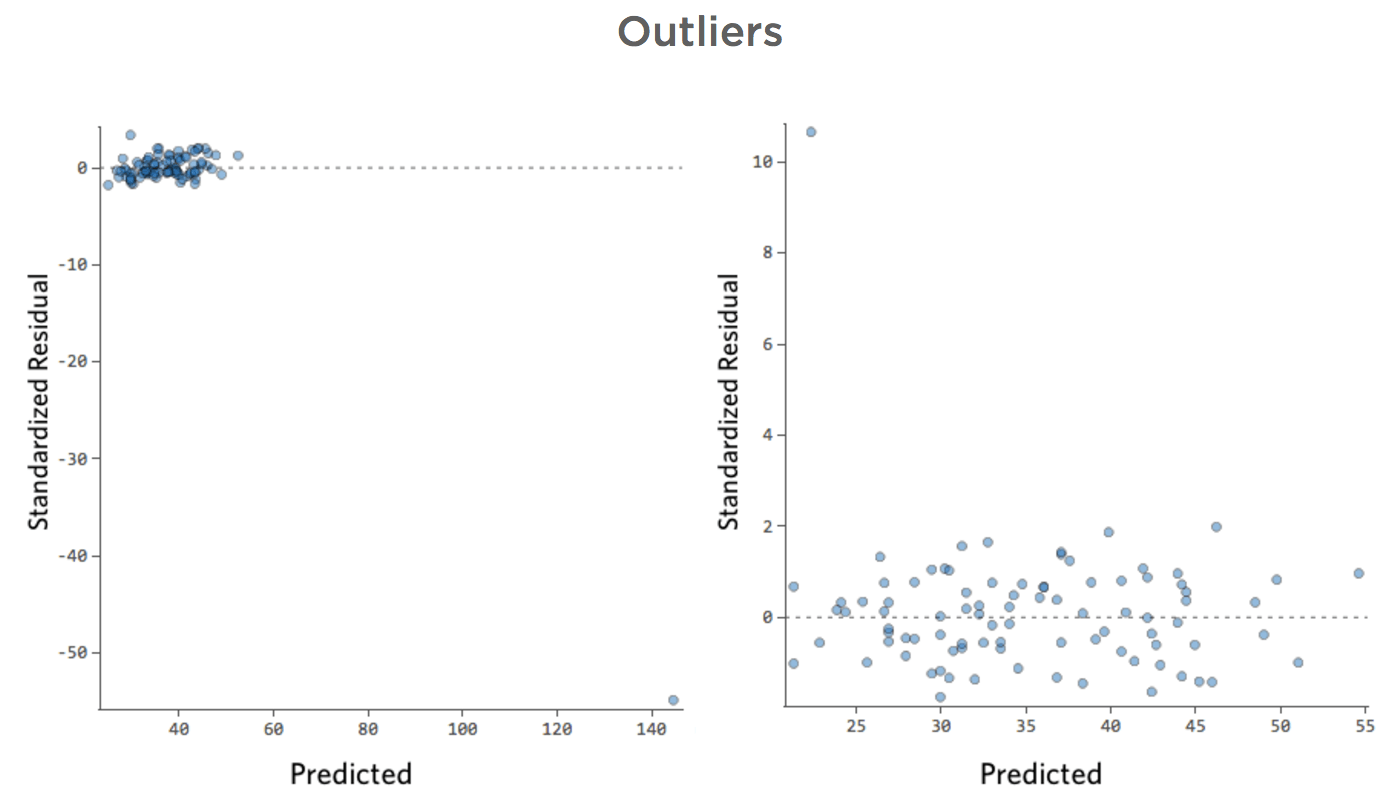
Veja algumas parcelas residuais que não atendem a esses requisitos:
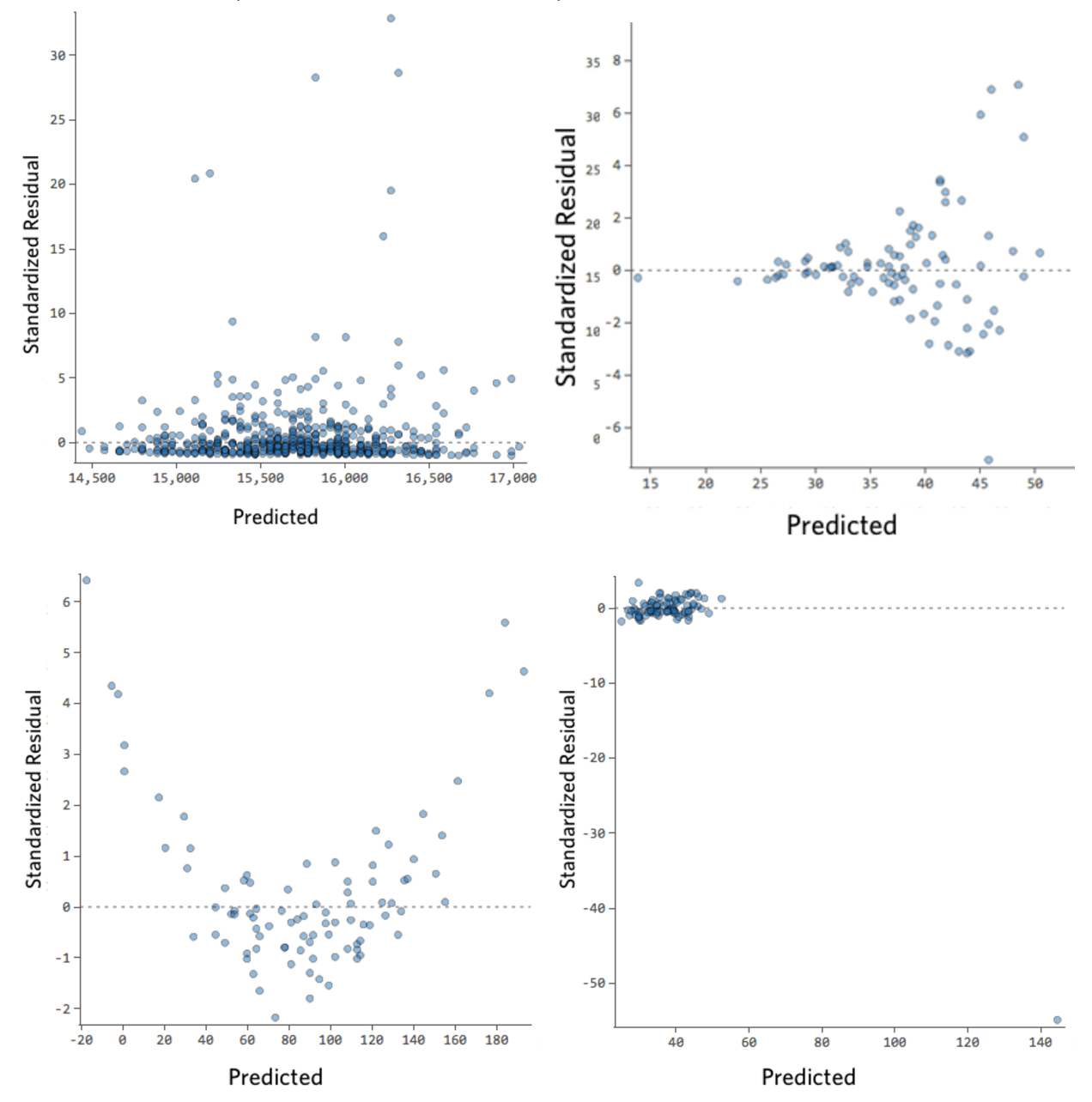
Esses diagramas não estão uniformemente distribuídas verticalmente, ou têm um contorno externo, ou têm uma forma clara para eles.
Se você conseguir detectar um padrão ou uma tendência clara em seus resíduos, seu modelo terá espaço para melhorias.
Em um segundo, vamos detalhar o porquê e o que fazer a respeito.
Parcela residual Q-Q normal:
Clique em Mostrar parcela residual Q-Q normal para exibir uma parcela Q-Q avaliando a distorção de dados e o ajuste do modelo. Este gráfico exibe os resíduos padronizados no eixo y e os quantis teóricos no eixo x.
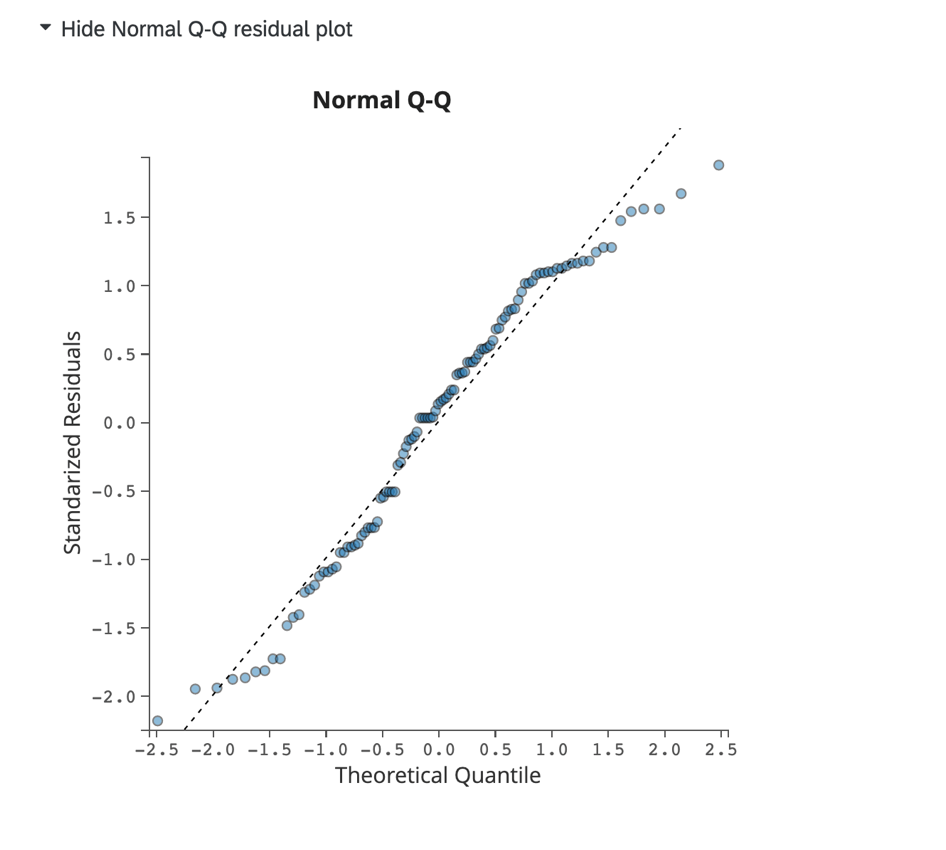 Dados alinhados com a linha pontilhada indicam uma distribuição normal. Se os pontos se afastarem drasticamente da linha, você pode considerar ajustar seu modelo adicionando ou removendo outras variáveis no modelo de regressão.
Dados alinhados com a linha pontilhada indicam uma distribuição normal. Se os pontos se afastarem drasticamente da linha, você pode considerar ajustar seu modelo adicionando ou removendo outras variáveis no modelo de regressão.
Quanto importa se meu modelo não é perfeito?
Até que ponto você deveria estar preocupado se seu modelo não é perfeito, se seus resíduos parecem um pouco insalubres? Depende de você.
Se você está publicando sua tese em física de partículas, provavelmente quer ter certeza de que seu modelo é o mais preciso possível. Se você está tentando fazer uma análise rápida e suja da barraca de limonada de seu sobrinho, um modelo menos do que perfeito pode ser bom o suficiente para responder a quaisquer perguntas que você tenha (por exemplo, se “Temperatura” parece afetar “Receita”).
Na maioria das vezes, um modelo decente é melhor do que nenhum. Portanto, pegue seu modelo, tente melhorá-lo e decida se a precisão é boa o suficiente para ser útil para seus fins.
Exemplo de parcelas residuais e seus diagnósticos
Se você não tiver certeza do que é um resíduo, reserve cinco minutos para ler o que está acima e volte aqui.
Abaixo está uma galeria de parcelas residuais insalubres. Seu resíduo pode parecer um tipo específico abaixo ou alguma combinação.
Se o seu parecer com um dos itens abaixo, clique nesse residual para entender o que está acontecendo e aprender a corrigi-lo.
(Durante a explicação, usaremos a “Receita” de uma barraquinha de limonada em comparação com a “Temperatura” desse dia como um conjunto de dados de exemplo.)
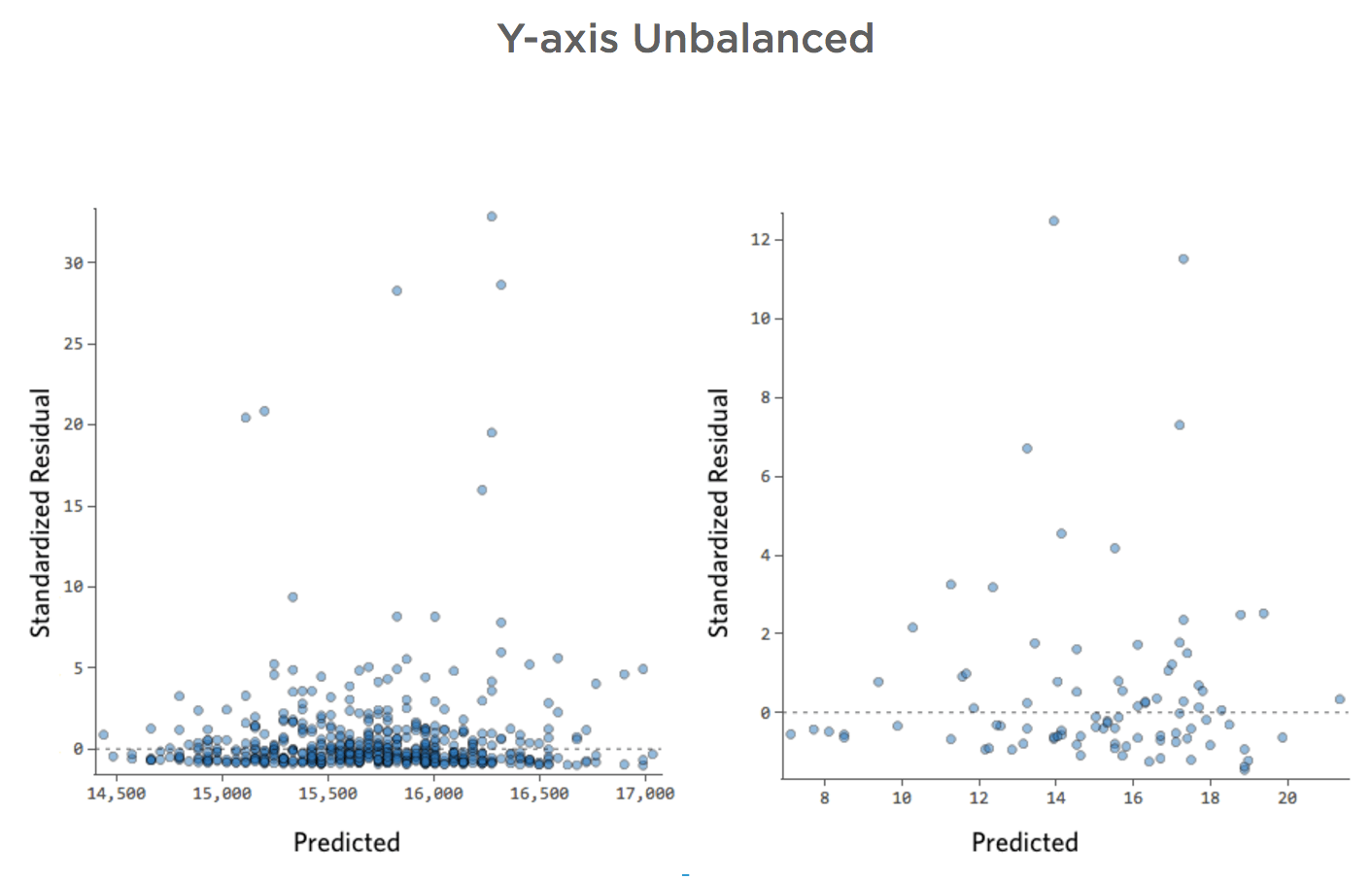
Desequilíbrio no eixo Y
- Mostrar detalhes sobre este diagrama e como corrigi-lo.
-
Problema
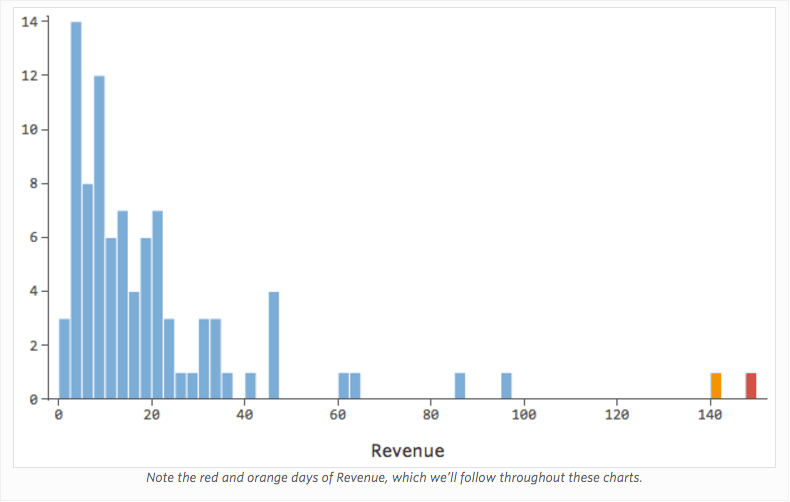
Imagine que, por qualquer motivo, sua barraca de limonada normalmente tem receita baixa, mas de vez em quando você obtém dias de receita muito alta, de tal forma que “Receita” parecia assim…
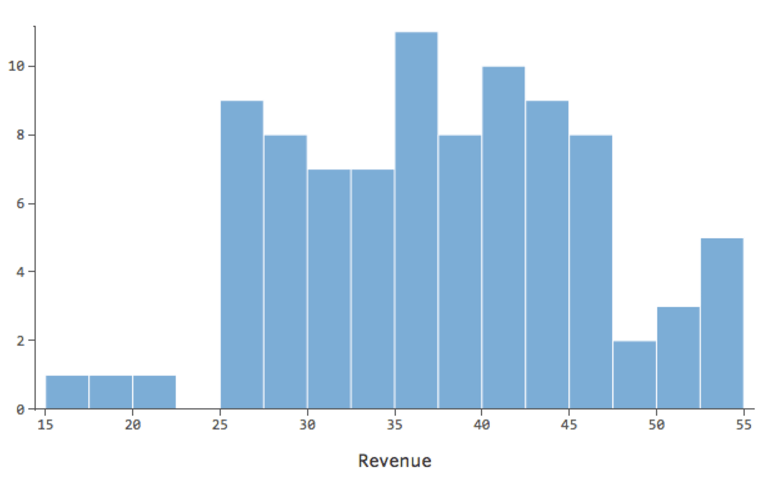
…em vez de algo mais simétrico e em forma de sino assim:
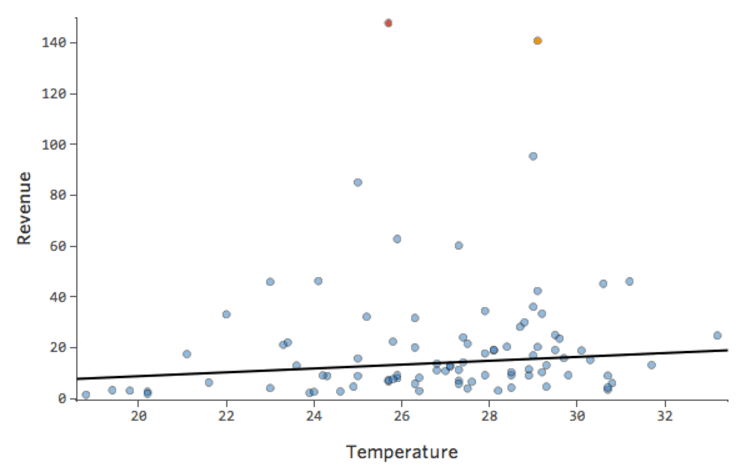
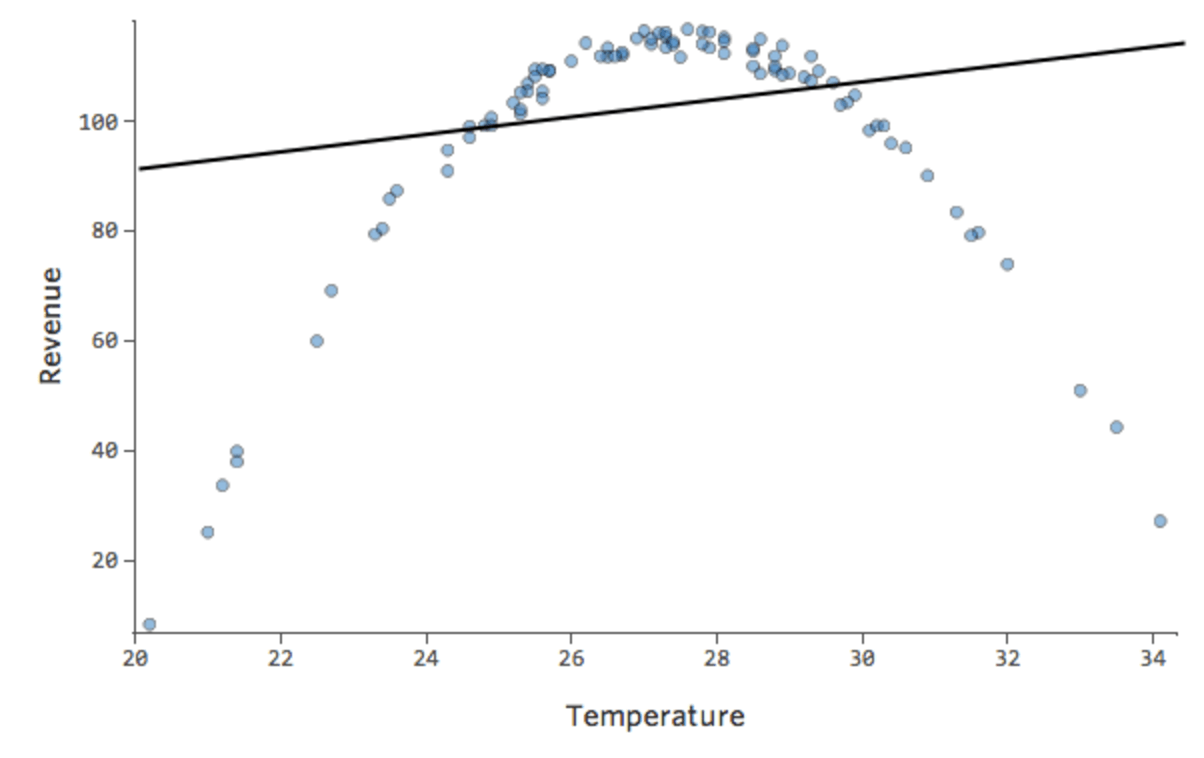
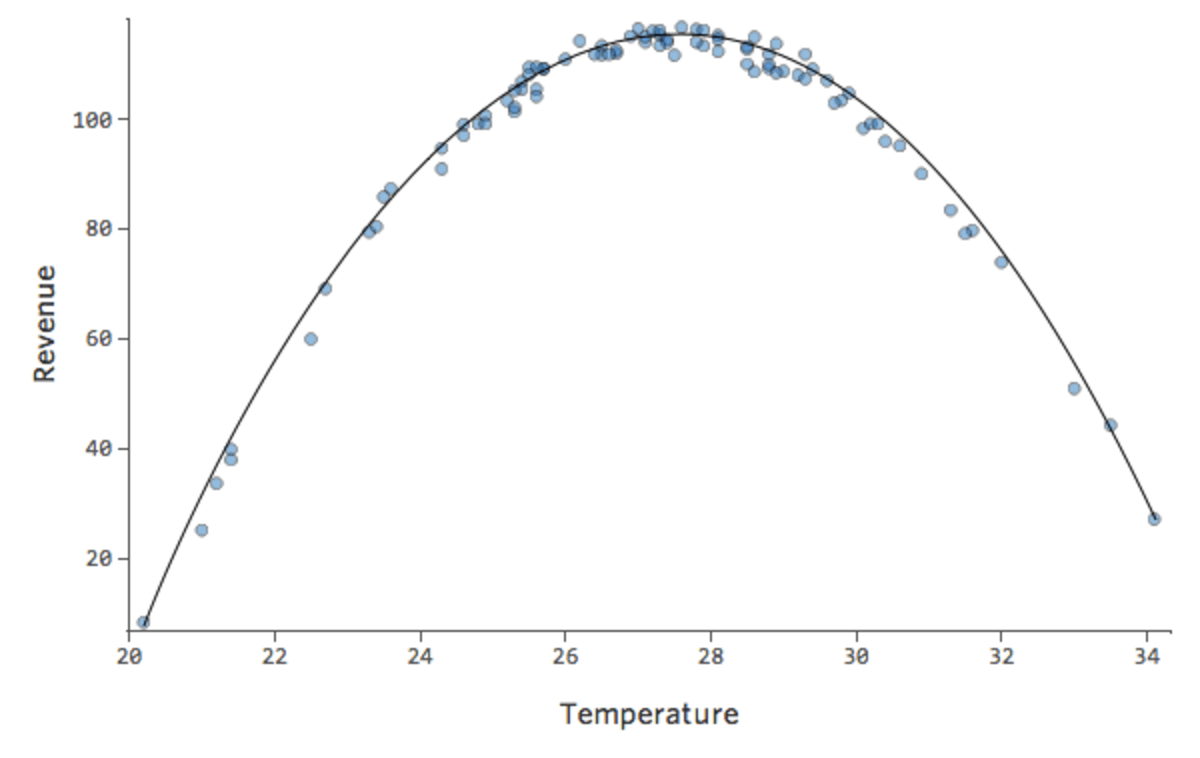
Então “Temperatura” vs. “Receita” pode parecer assim, com a maioria dos dados agrupados na parte inferior…
A linha preta representa a equação do modelo, a previsão do modelo da relação entre “Temperatura” e “Receita”. Veja acima cada previsão feita pela linha preta para uma determinada “Temperatura” (por exemplo, em “Temperatura” 30, “Receita” está previsto para ser cerca de 20). Você pode ver que a maioria dos pontos está abaixo da linha (ou seja, a previsão foi muito alta), mas alguns pontos estão muito acima da linha (ou seja, a previsão foi muito baixa).
Traduzindo esses mesmos dados para os gráficos de diagnóstico, a maioria das previsões da equação é um pouco alta demais, e então algumas seriam muito baixas.
Implicações
Isso quase sempre significa que seu modelo pode ser tornado significativamente mais preciso. Na maioria das vezes, você verá que o modelo estava direcionado corretamente, mas bastante impreciso em relação a uma versão melhorada. Não é incomum corrigir um problema como este e, consequentemente, ver o salto de coeficiente de determinação do modelo de 0,2 para 0,5 (em uma escala de 0 a 1).
Como corrigir
- A solução para isto é quase sempre transformar seus dados, normalmente sua variável de resposta .
- Também é possível que seu modelo não tenha uma variável.
Heteroscedasticidade
- Mostrar detalhes sobre esta parcela e como corrigi-la.
-
Problema
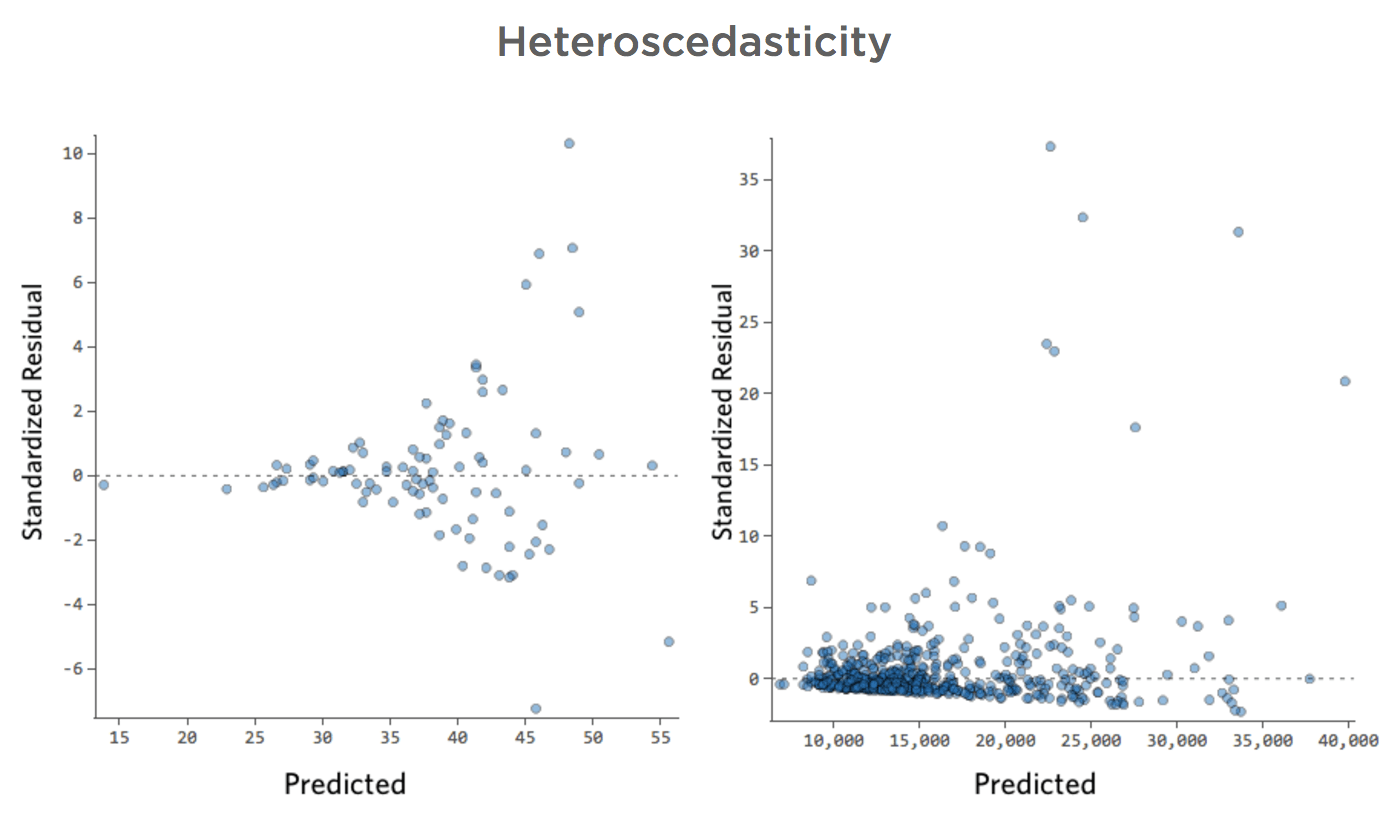
Esses diagramas exibem “heteroscedasticidade”, o que significa que os resíduos ficam maiores à medida que a previsão se move de pequena para grande (ou de grande para pequena).
Imagine que em dias frios, a quantidade de receita é muito consistente, mas em dias mais quentes, às vezes a receita é muito alta e às vezes é muito baixa.
Você veria gráficos como estes:
Implicações
Isso não cria inerentemente um problema, mas muitas vezes é um indicador de que seu modelo pode ser melhorado.
A única exceção aqui é que se seu tamanho de amostra for inferior a 250, e você não puder corrigir o problema usando os valores de p abaixo, seus valores de p podem ser um pouco maiores ou menores do que deveriam ser, portanto, possivelmente uma variável que esteja correta na margem de importância pode acabar erroneamente no lado errado dessa margem. Seus coeficientes de regressão (o número de unidades de “Receita” muda quando a “Temperatura” sobe um) ainda serão precisos, no entanto.
Como corrigir
- A solução bem-sucedida mais frequente é transformar uma variável.
- Muitas vezes, a heteroscedasticidade indica que uma variável está ausente.
Não linear
- Mostrar detalhes sobre esta parcela e como corrigi-la.
-
Problema
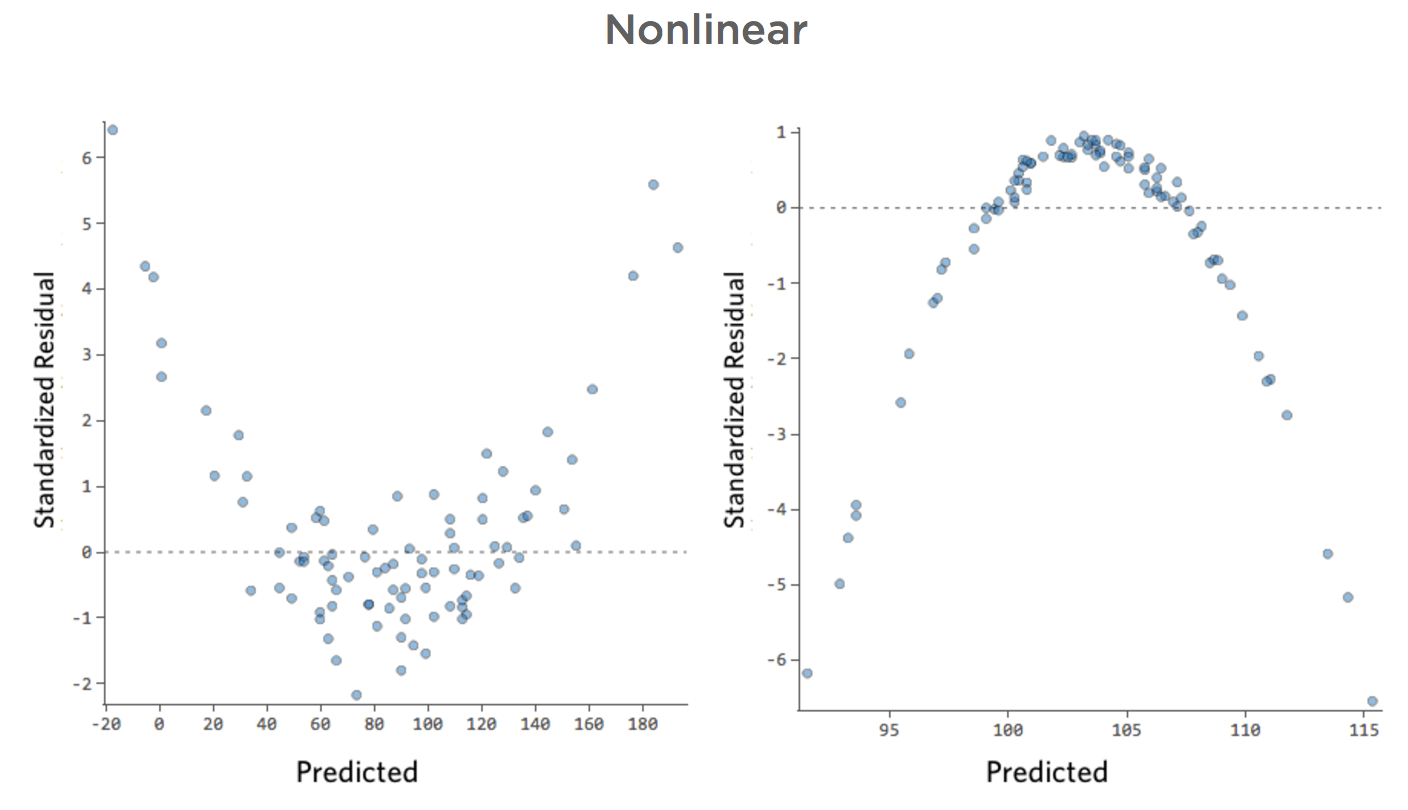
Imagine que é difícil vender limonada em dias frios, fácil vendê-la em dias quentes e difícil vendê-la em dias muito quentes (talvez porque ninguém saia de sua casa em dias muito quentes).
Esse diagrama ficaria assim:
O modelo, representado pela linha, é terrível. As previsões estariam desviadas, o que significa que seu modelo não representa com precisão a relação entre “Temperatura” e “Receita”.
Assim, os resíduos ficariam desta forma:
Implicações
Se seu modelo estiver desviado, como no exemplo acima, suas previsões serão bastante inúteis (e você notará um coeficiente de determinação muito baixo, como o coeficiente de determinação 0,027 para o acima).
Outras vezes, um ajuste um pouco abaixo do ideal ainda lhe dará uma boa noção geral da relação, mesmo que não seja perfeito, como abaixo:
Esse modelo parece bastante preciso. Se você olhar de perto (ou se olhar os resíduos), pode dizer que há um pouco de um padrão aqui – que os pontos estão em uma curva que a linha não corresponde bem.
Isso importa? Depende de você. Se você está conseguindo uma rápida compreensão da relação, sua reta é uma aproximação bem decente. Se você for usar este modelo para previsão e não para explicação, o modelo mais preciso possível provavelmente levaria em conta essa curva.
Como corrigir
- Às vezes, padrões como este indicam que uma variável precisa ser transformada.
- Se o padrão for realmente tão claro quanto esses exemplos, você provavelmente precisará criar um modelo não linear (não é tão difícil quanto parece).
- Ou, como sempre, é possível que o problema seja uma variável ausente.
Anomalias
- Mostrar detalhes sobre esta parcela e como corrigi-la.
-
Problema
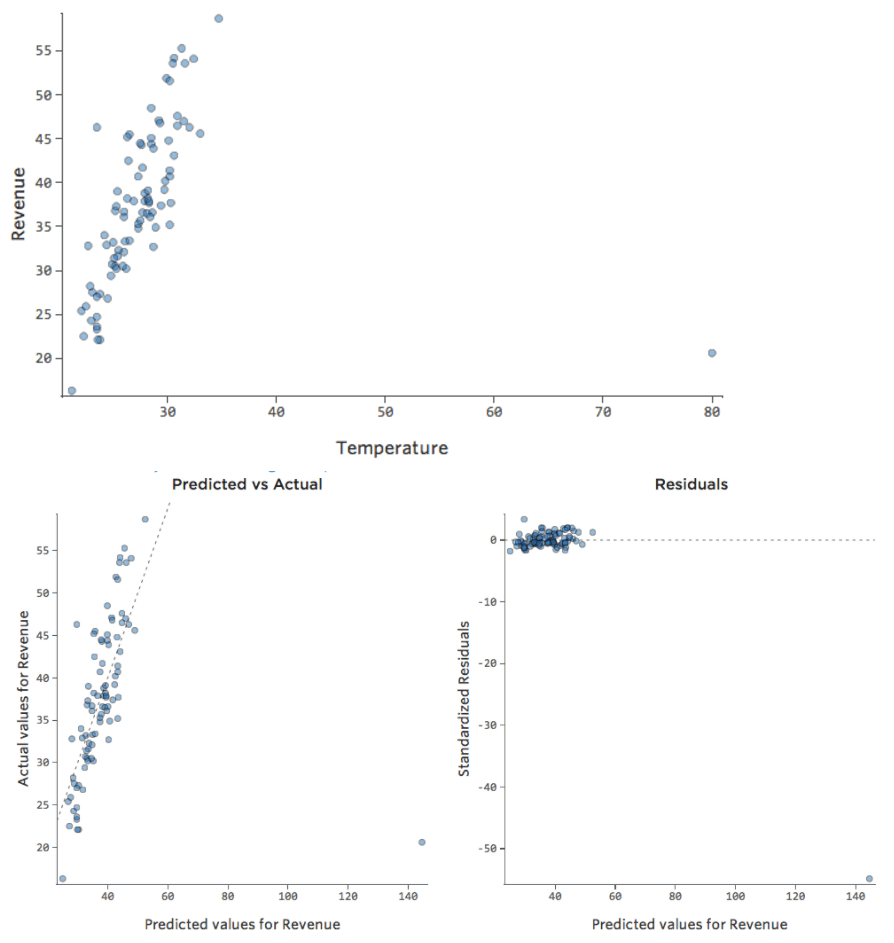
E se um de seus pontos de referência tivesse uma “Temperatura” de 80 em vez dos normais 20 e 30? Seus diagramas teriam o seguinte aspecto:
Essa regressão tem um ponto de dados distante em uma variável de entrada, “Temperatura” (anomalias em uma variável de entrada também são conhecidas como “pontos de alavancagem”).
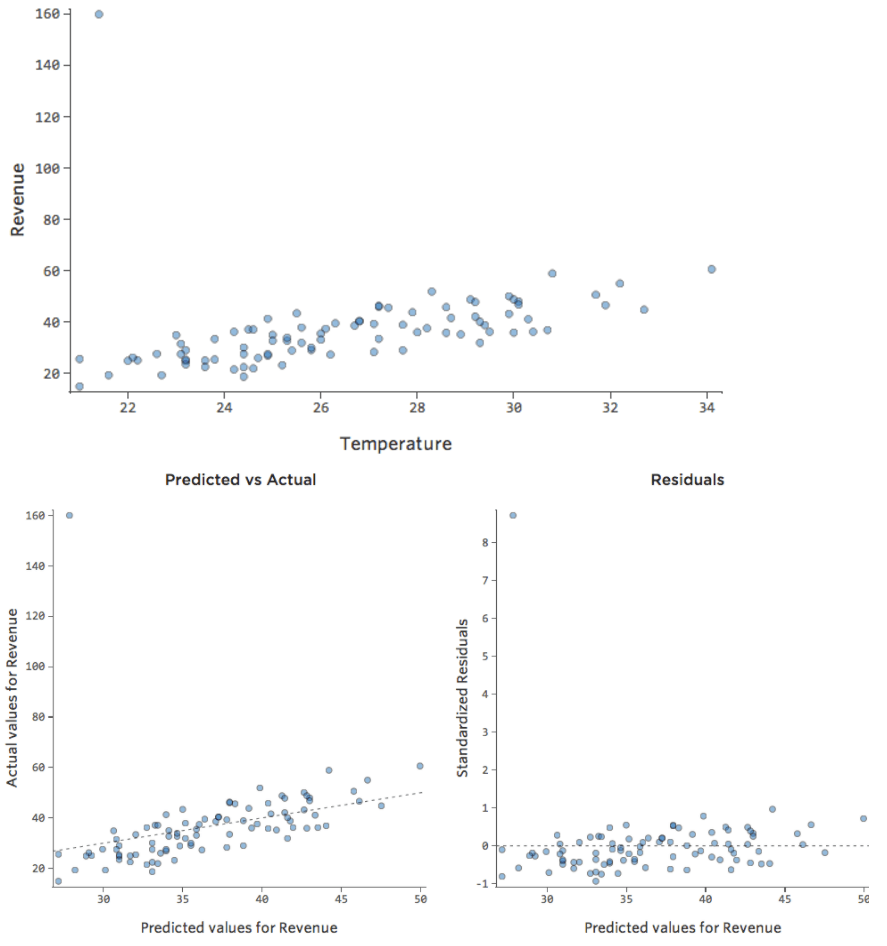
E se um de seus pontos de referência tivesse US$ 160 em receita em vez dos normais US$ 20 – US$ 60? Seus diagramas teriam o seguinte aspecto:
Essa regressão tem um ponto de dados distante em uma variável de saída, “Receita”.
Implicações
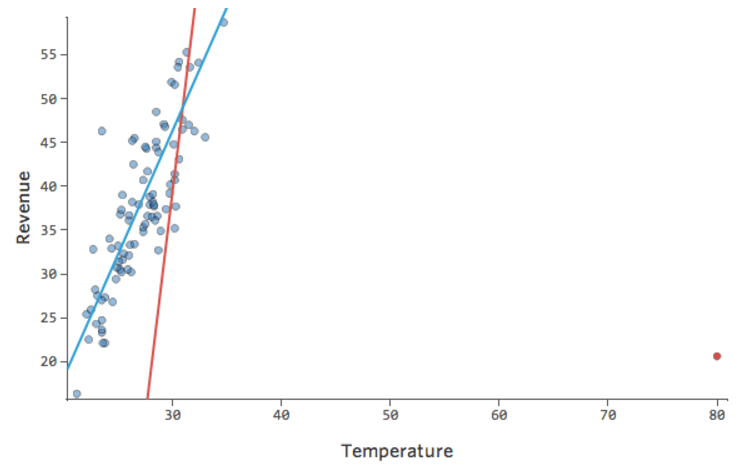
O Stats iQ executa um tipo de regressão que geralmente não é afetado por anomalias de saída (como o dia com receita de $ 160), mas é afetado por anomalias de entrada (como uma “Temperatura” nos 80). No pior caso, seu modelo pode se articular para tentar se aproximar daquele ponto às custas de estar perto de todos os outros e acabar sendo completamente errado, assim:
A linha azul é provavelmente como você gostaria que seu modelo fosse exibido, e a linha vermelha é o modelo que você poderá ver se tiver esse valor atípico em “Temperatura” 80.
Como corrigir
- É possível que se trate de um erro de medição ou de entrada de dados, em que a anomalia está incorreta e, nesse caso, você deve eliminá-la.
- É possível que o que parece ser apenas um par de anomalias seja, de fato, uma distribuição de forças. Considere transformar a variável se uma de suas variáveis tiver uma distribuição assimétrica (ou seja, não está remotamente em forma de sino).
- Se for realmente um valor anômalo legítimo, você deve avaliar o impacto da anomalia.
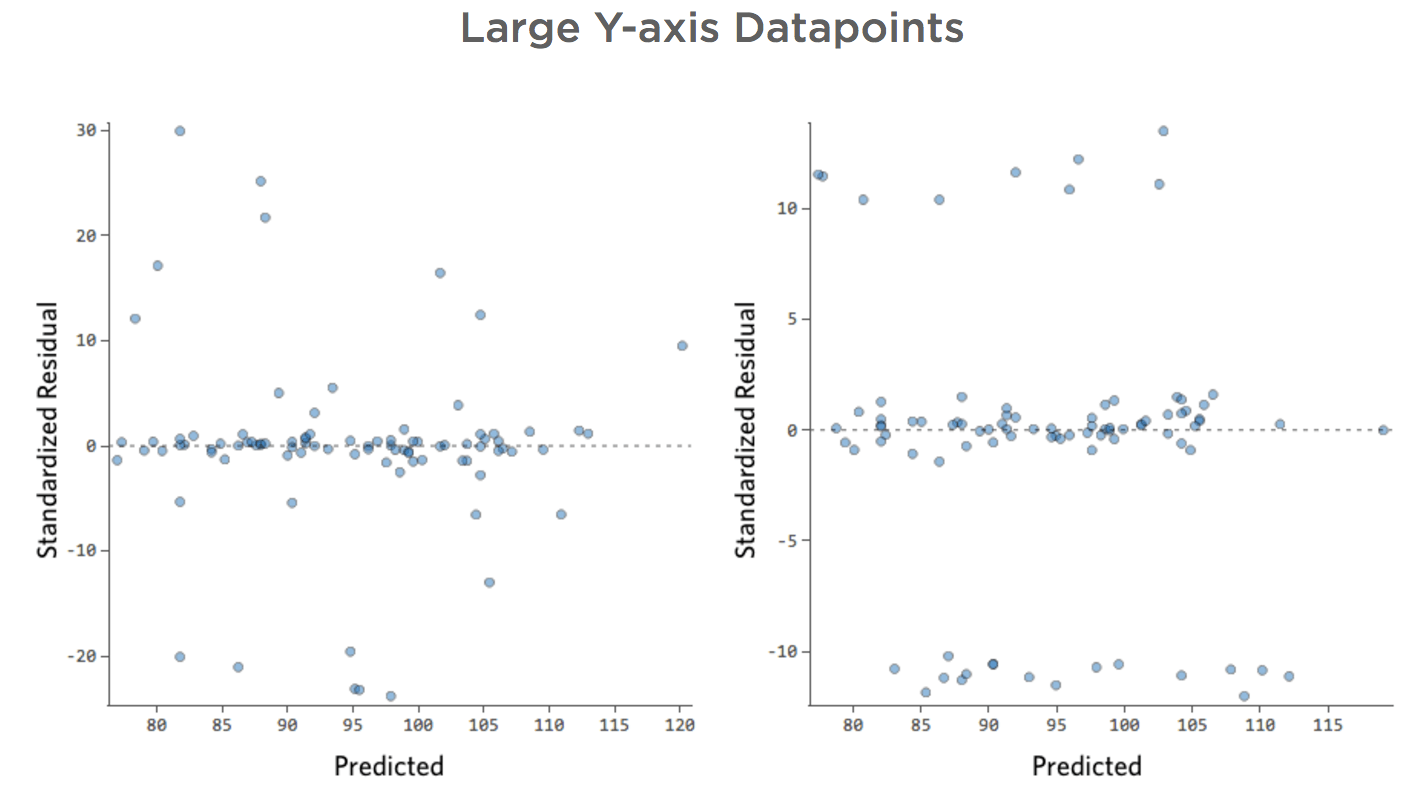
Pontos de dados grandes do eixo Y
- Mostrar detalhes sobre este diagrama e como corrigi-lo.
-
Problema
Imagine que há duas barracas concorrentes de limonada nas proximidades. Na maioria das vezes, apenas um está operacional, caso em que sua receita é consistentemente boa. Às vezes, nenhum deles é ativo e a receita sobe; em outros momentos, ambos estão ativos e a receita despenca.
“Receita” vs. “Temperatura” pode ser assim…
…com essa linha superior sendo dias em que nenhuma outra posição aparece e a linha inferior sendo dias em que ambas as barracas estão nos negócios.
Isso resultaria em gráficos residuais:
Ou seja, há muitos pontos de dados em ambos os lados de 0 que têm resíduos de 10 ou mais, o que significa que o modelo estava muito distante.
Agora, se você coletasse dados todos os dias para uma variável chamada “Número de barracas de limonada ativas”, você poderia adicionar essa variável ao seu modelo e esse problema seria corrigido. Mas muitas vezes você não tem os dados de que precisa (ou até mesmo um palpite sobre qual tipo de variável você precisa).
Implicações
Seu modelo não é inútil, mas definitivamente não é tão bom quanto se você tivesse todas as variáveis necessárias. Você ainda poderia usá-lo e poderia dizer algo como: “Esse modelo é bem preciso na maioria das vezes, mas depois de vez em quando fica muito distante”. Isso é útil? Provavelmente, essa é a sua decisão e depende de quais decisões você está tentando tomar com base em seu modelo.
Como corrigir
- Embora essa abordagem não funcione no exemplo específico acima, quase sempre vale a pena olhar para ver se há uma oportunidade de transformar uma variável com utilidade.
- No entanto, se isso não funcionar, você provavelmente precisará lidar com seu problema de variável ausente.
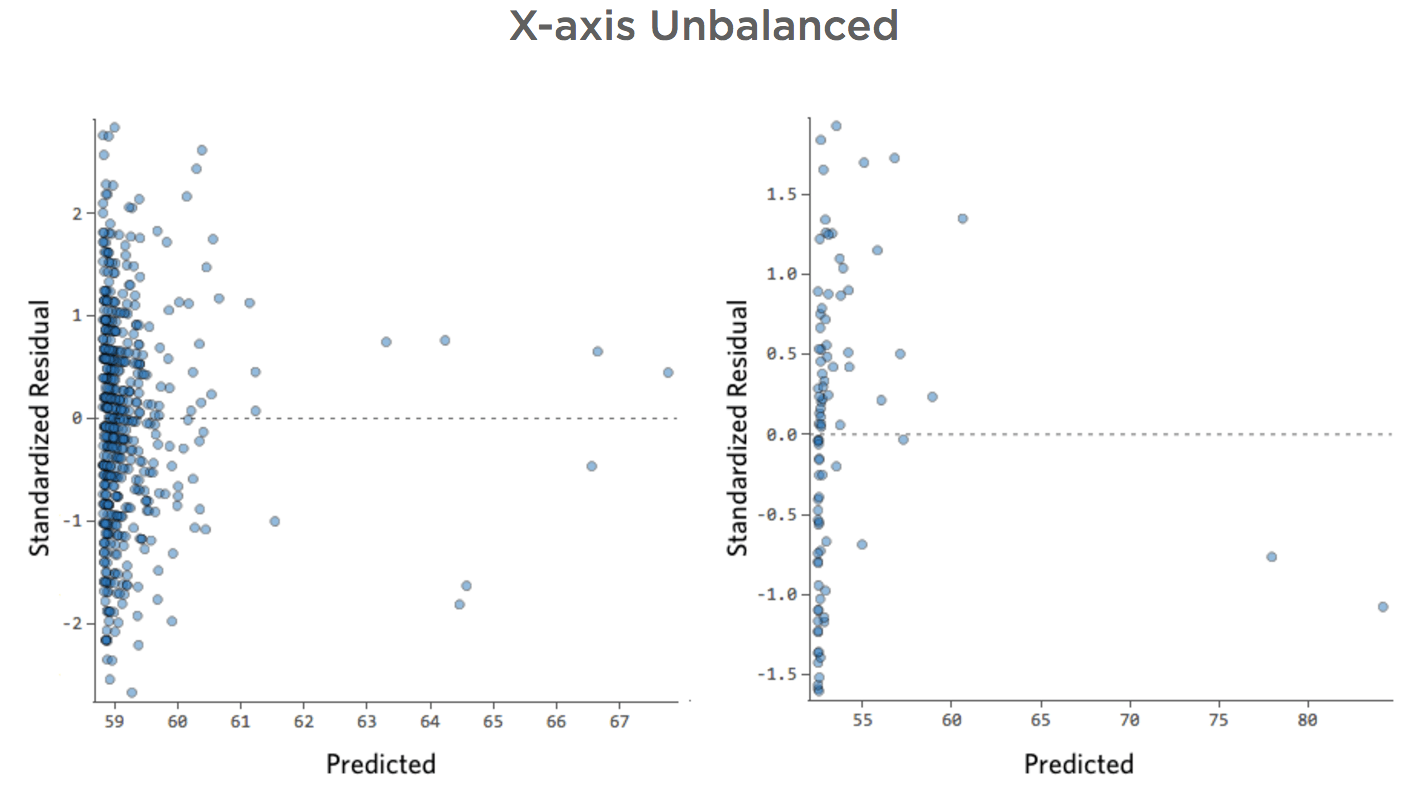
Eixo X desbalanceado
- Mostrar detalhes sobre esta parcela e como corrigi-la.
-
Problema
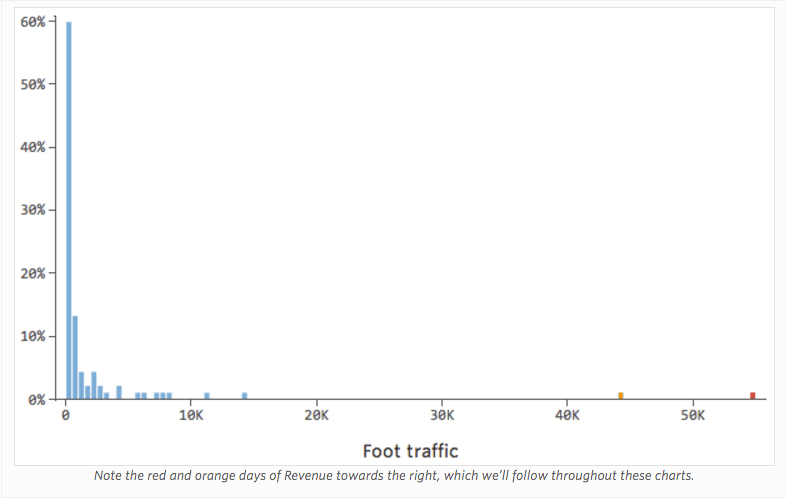
Imagine que a “Receita” é impulsionada pelo “tráfego a pé” nas proximidades, além ou em vez de apenas “Temperatura”. Imagine que, por qualquer motivo, sua barraca de limonada normalmente tem receita baixa, mas de vez em quando você obtém dias extremamente altos de receita, de modo que sua receita foi assim…
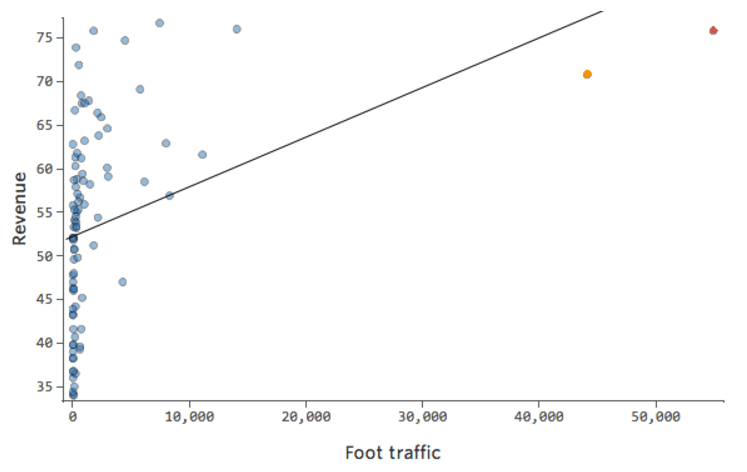
Então “Tráfego a pé” vs. “Receita” pode ter o seguinte aspecto, com a maioria dos dados agrupados no lado esquerdo:
A linha preta representa a equação do modelo, a previsão do modelo da relação entre “tráfego a pé” e “Receita”. Você pode ver que o modelo não consegue realmente dizer a diferença entre o “tráfego a pé” de 0 e de, digamos, 100 ou 1.000; para cada um desses valores, ele preveria uma receita próxima de $ 53.
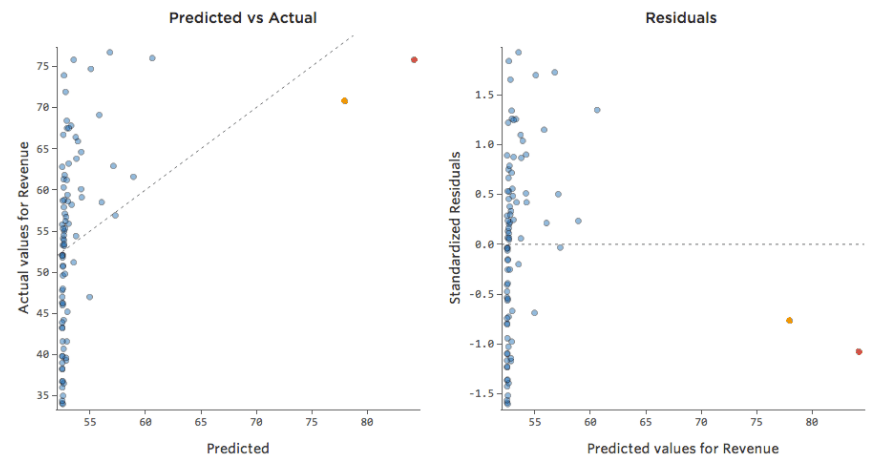
Traduzindo esses mesmos dados para os diagramas de diagnóstico:
Implicações
Às vezes não há nada de errado com seu modelo. No exemplo acima, fica bem claro que esse não é um bom modelo, mas às vezes o gráfico residual está desequilibrado e o modelo é muito bom.
As únicas maneiras de dizer são para a) experimentar a transformação de seus dados e ver se você pode melhorá-los e b) olhar para o diagrama previsto vs. real e ver se sua previsão está muito errada para muitos pontos de dados, como no exemplo acima (mas diferente do exemplo abaixo).
Embora não exista uma regra explícita que diga que seu resídu não pode ser desequilibrado e ainda ser preciso (na verdade, esse modelo é bastante preciso), é mais frequente que um resíduo de eixo x desequilibrado signifique que seu modelo pode ser tornado significativamente mais preciso. Na maioria das vezes, você verá que o modelo estava direcionado corretamente, mas bastante impreciso em relação a uma versão melhorada. Não é incomum corrigir um problema como este e, consequentemente, ver o salto de coeficiente de determinação do modelo de 0,2 para 0,5 (em uma escala de 0 a 1).
Como corrigir
- A solução para isso é quase sempre transformar seus dados, normalmente uma variável explicativa. (Observe que o exemplo mostrado abaixo fará referência à transformação de sua variável de resposta , mas o mesmo processo será útil aqui.)
- Também é possível que seu modelo não tenha uma variável.
Melhorando seu modelo: avaliação do impacto de um valor atípico
Vamos supor que você tem um ponto de dados distante que é legítimo, não uma medição ou um erro de dados. Para decidir como avançar, você deve avaliar o impacto do ponto de dados na regressão.
A maneira mais fácil de fazer isso é anotar os coeficientes do seu modelo atual e filtrar esse ponto de dados da regressão. Se o modelo não muda muito, então você não tem muito com o que se preocupar.
Se isso modificar o modelo significativamente, examine o modelo (especialmente real vs. previsto) e decida qual deles é melhor para você. Não há problema em descartar o mais distante, desde que você possa teoricamente defender isso, dizendo: “Neste caso, não estamos interessados em anomalias, eles simplesmente não são de interesse”, ou “Esse foi o dia em que o tio Jerry veio comprar e me deu uma gorjeta de 100 dólares; isso não é previsível e não vale a pena incluir no modelo”.
Melhorando seu modelo: transformando variáveis
Visão geral
A forma mais comum de melhorar um modelo é transformar uma ou mais variáveis, geralmente usando uma transformação “log”.
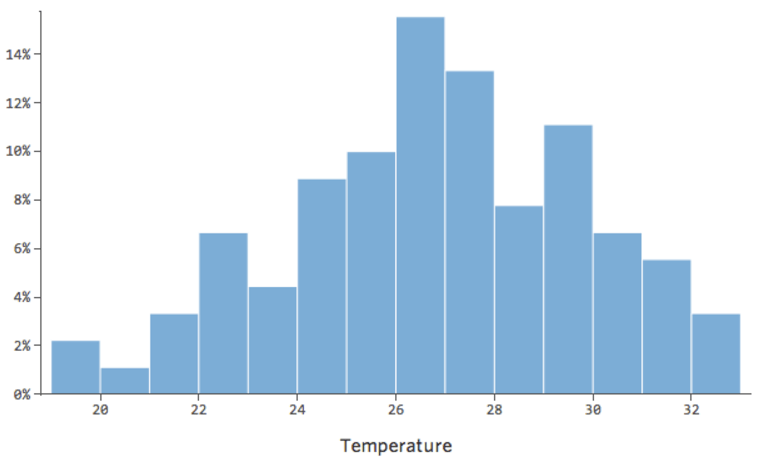
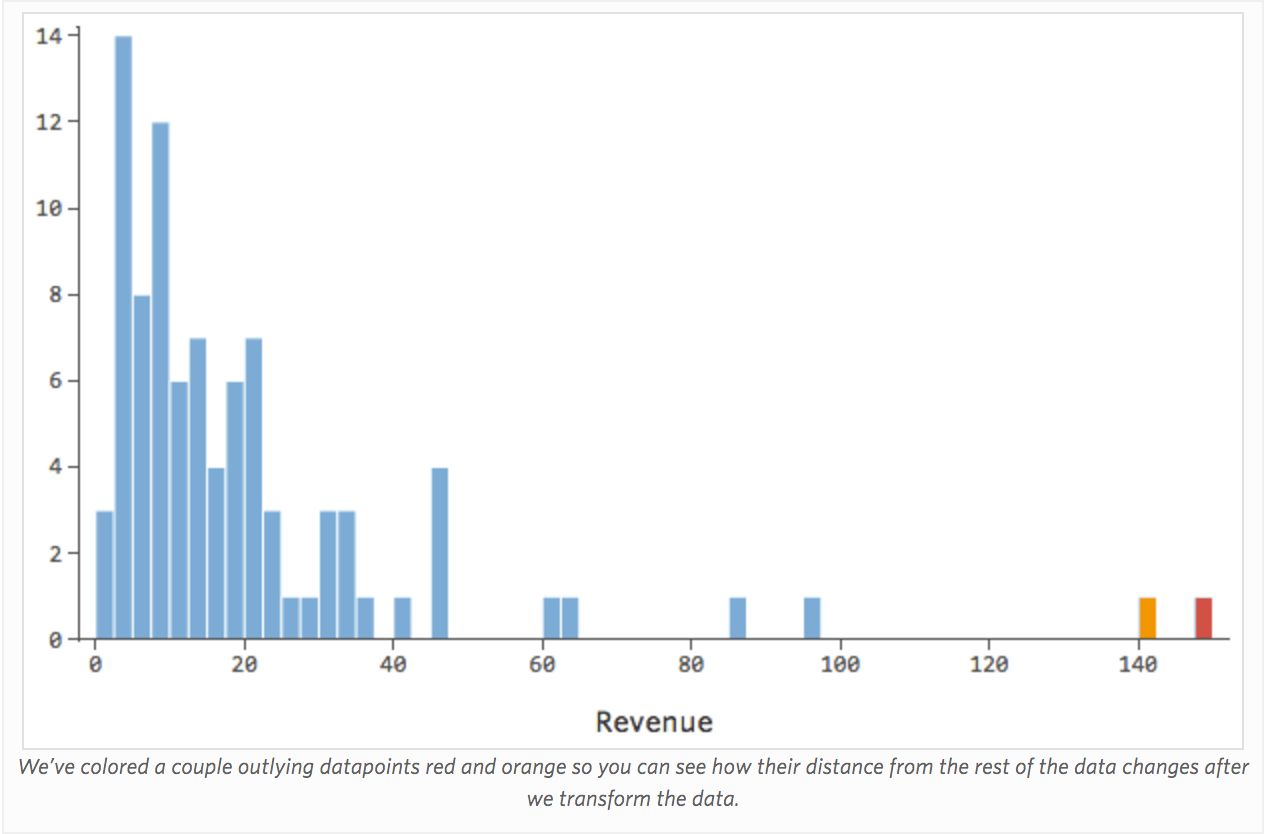
A transformação de uma variável muda a forma de sua distribuição. Normalmente, o melhor lugar para começar é uma variável que tem uma distribuição assimétrica, em oposição a uma distribuição mais simétrica ou em forma de sino. Encontre uma variável como esta para transformar:
Em geral, os modelos de regressão funcionam melhor com curvas mais simétricas em forma de sino. Experimente diferentes tipos de transformações até atingir a mais próxima dessa forma. Muitas vezes não é possível chegar perto disso, mas esse é o objetivo. Então, digamos que você pegue a raiz quadrada da “Receita” como uma tentativa de chegar a uma forma mais simétrica, e sua distribuição tem o seguinte aspecto:
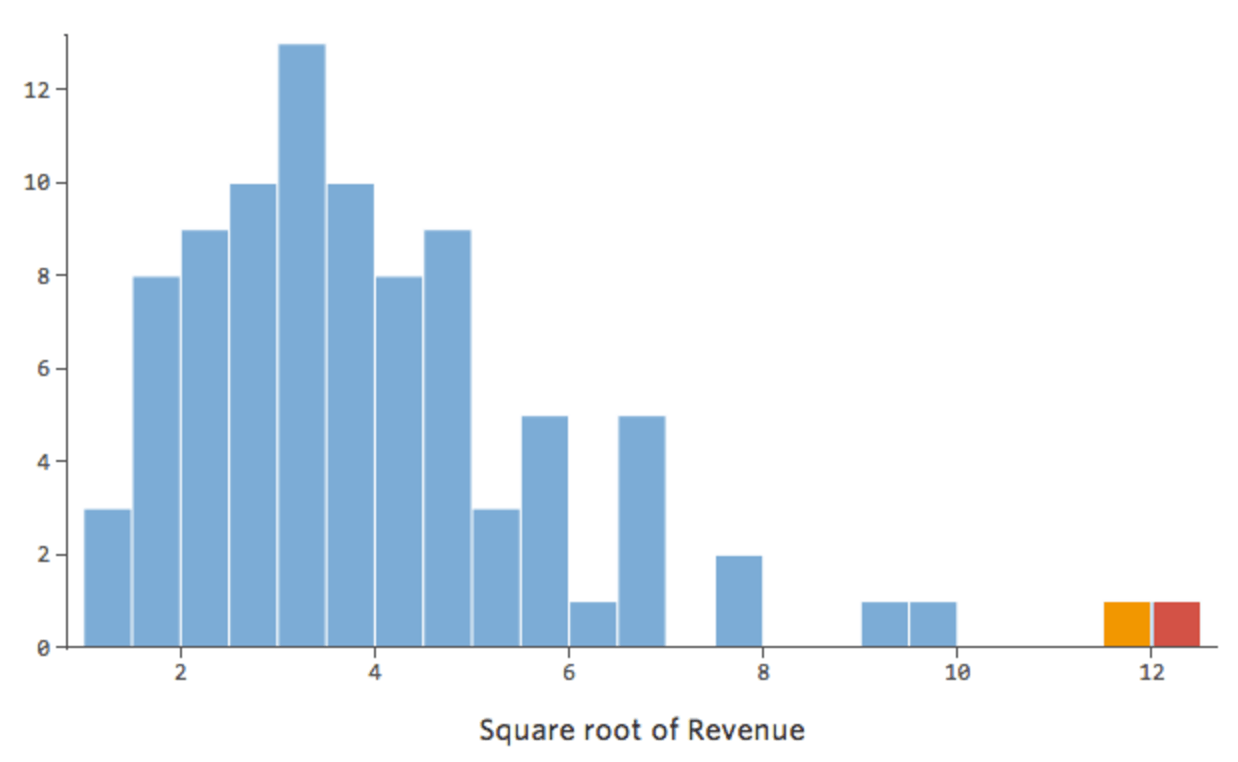
Isso é bom, mas ainda é um pouco assimétrico. Vamos tentar tomar o log da “Receita” em vez disso, o que produz esta forma:
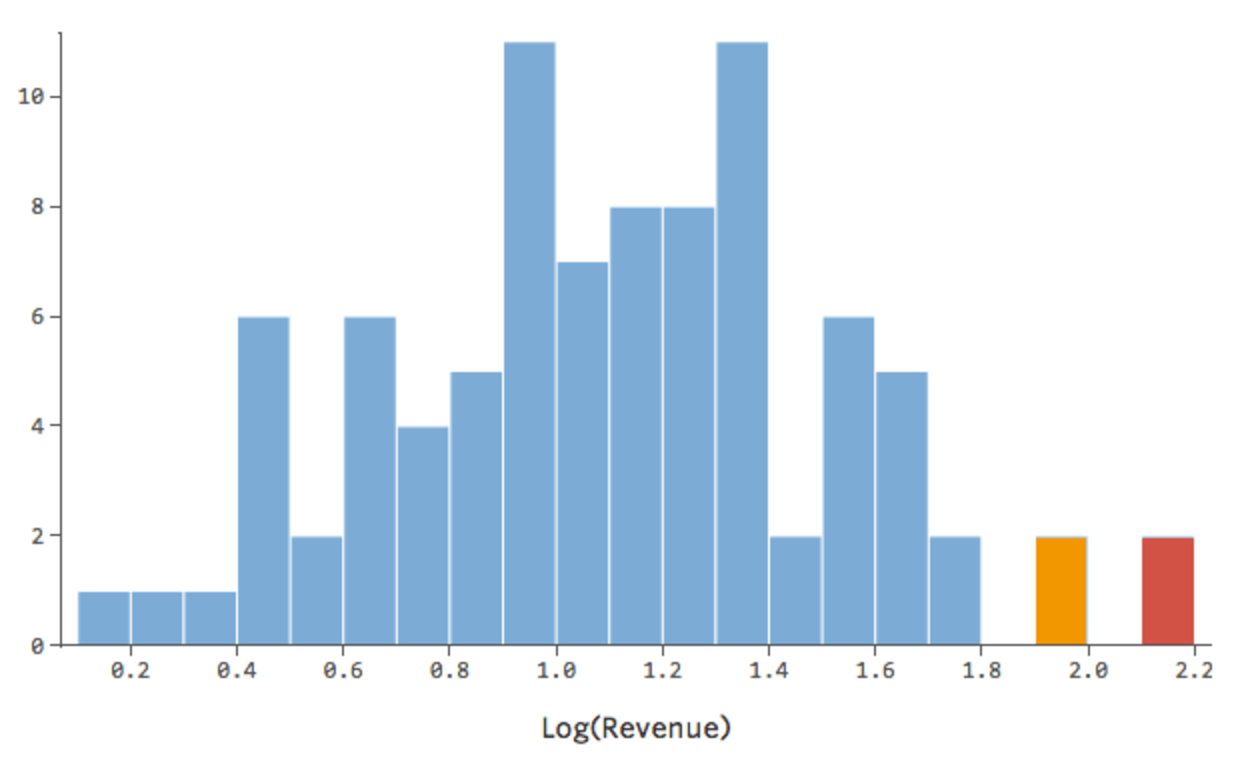
Isso é agradável e simétrico. Você provavelmente vai obter um modelo de regressão melhor com log (“Receita”) em vez de “Receita”. De fato, veja como sua equação, seus resíduos e seu coeficiente de determinação podem mudar:
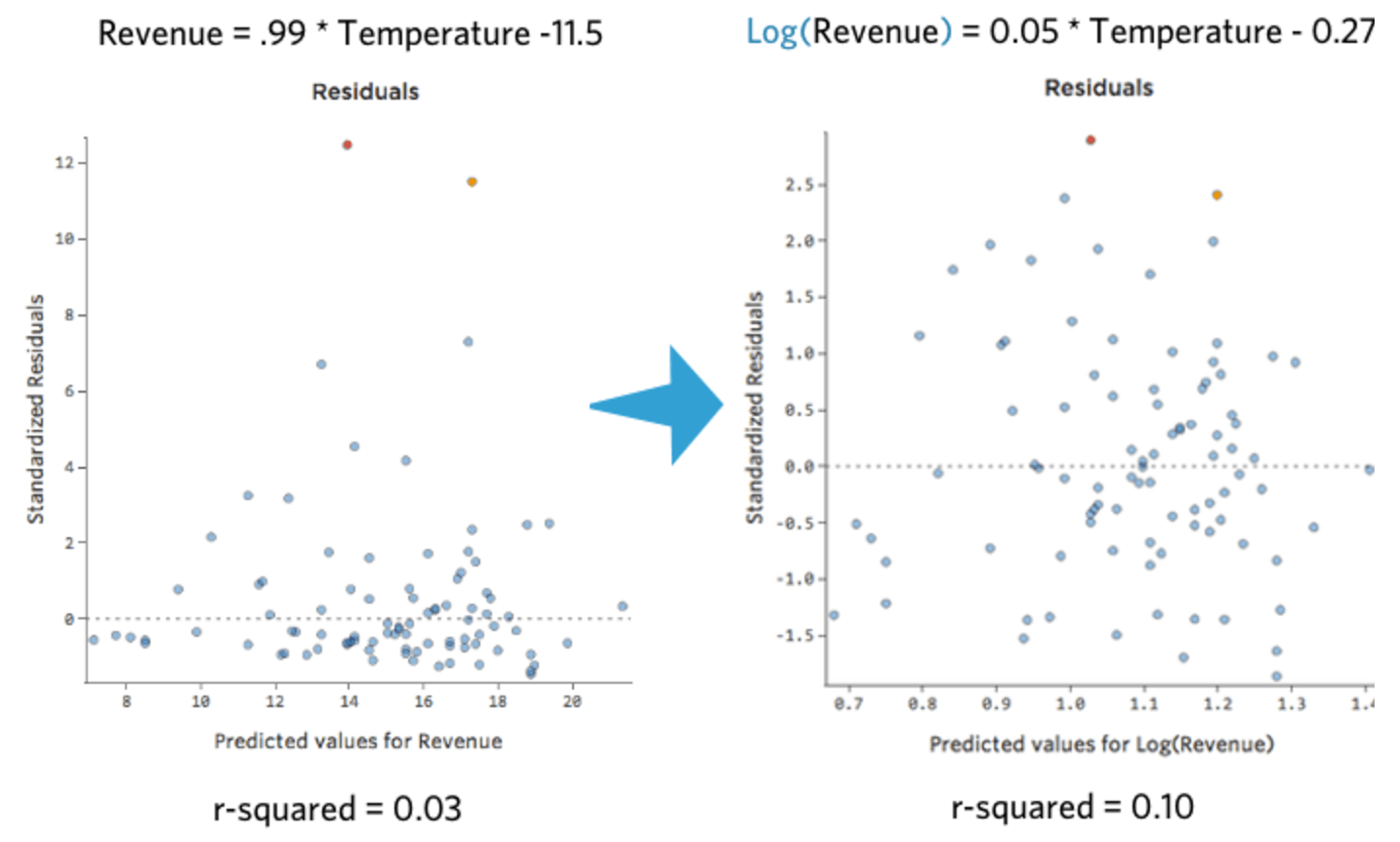
O Stats iQ mostra uma versão pequena da distribuição da variável em linha com a equação de regressão: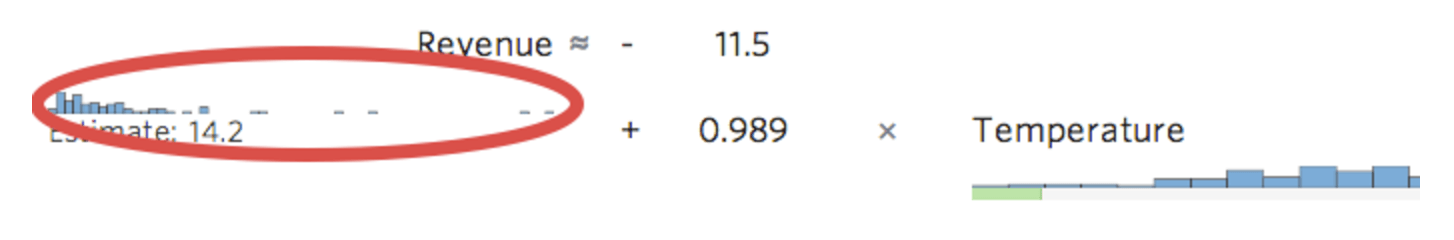
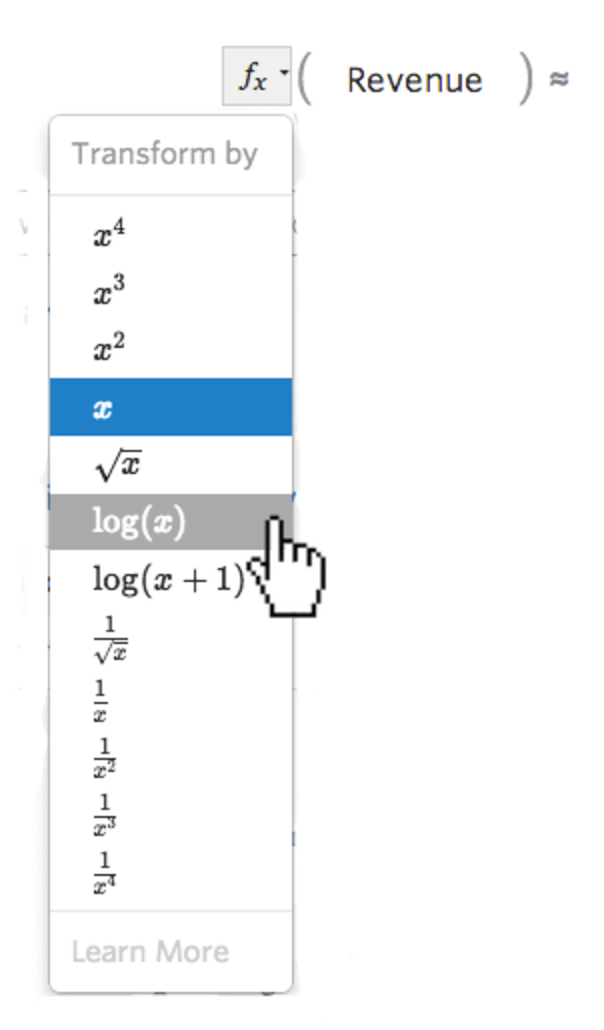
Selecione o botão fx de transformação à esquerda da variável…
…em seguida, selecione uma transformação, na maioria das vezes log(x)...
…depois examine o histograma para ver se ele está mais centrado, como este é depois da transformação:

Após a transformação de uma variável, observe como sua distribuição, o coeficiente de determinação da regressão e os padrões do diagrama residual mudam. Se isso melhorar (especialmente o coeficiente de determinação e os resíduos), provavelmente é melhor manter a transformação.
Se for necessária uma transformação, você deve começar por uma transformação “log”, pois os resultados do seu modelo ainda serão fáceis de entender. Observe que você encontrará problemas se os dados que você está tentando transformar incluírem zeros ou valores negativos. Para saber por que usar um registro é tão útil, ou se você tem números não positivos que deseja transformar, ou se você só quer obter uma melhor compreensão do que está acontecendo quando transforma dados, leia os detalhes abaixo.
Detalhes
Calcular o log10() de um número é o mesmo que perguntar “10 elevado a que potência resulta nesse número?”. Por exemplo, aqui está uma tabela simples de quatro pontos de dados, incluindo “Receita” e Log (“Receita”):
| Temperatura | Receita | Log (Receita) |
|---|---|---|
| 20 | 100 | 2 |
| 30 | 1.000 | 3 |
| 40 | 10.000 | 4 |
| 45 | 31.623 | 4,5 |
Observe que se plotarmos “Temperatura” vs. “Receita” e “Temperatura” vs. Log (“Receita”), o último modelo se ajusta muito melhor.
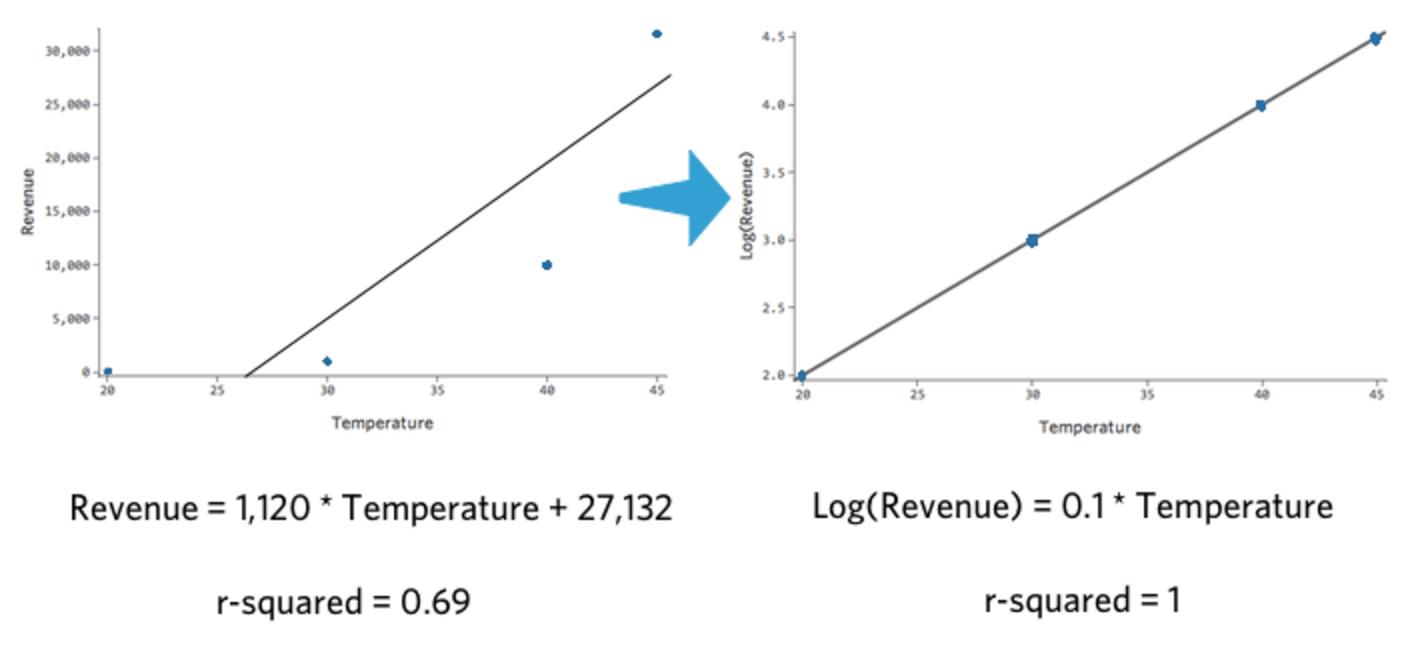
O interessante sobre essa transformação é que sua regressão não é mais linear. Quando “Temperatura” passou de 20 para 30, “Receita” passou de 10 para 100, um gap de 90 unidades. Então, quando “Temperatura” passou de 30 para 40, “Receita” passou de 100 para 1000, um gap muito maior.
Se você calculou um log da sua variável de resposta, não significa mais que um aumento de uma unidade em “Temperatura” resulta em um aumento de X unidades em “Receita”. Agora é um aumento de Xpor cento na “Receita”. Neste caso, um aumento de dez unidades em “Temperatura” está associado a um aumento de 1000% em Y – ou seja, um aumento de uma unidade em “Temperatura” está associado a um aumento de 26% na “Receita”.
Observe também que você não pode pegar o log de 0 ou de um número negativo (não há X onde 10X = 0 ou 10X= -5), então se você fizer uma transformação de log, perderá esses pontos de dados da regressão. Existem 4 formas comuns de lidar com a situação:
- Pegue uma raiz quadrada ou uma raiz cúbica. Eles não mudarão a forma da curva tão drasticamente quanto tomar um log, mas permitem que os zeros permaneçam na regressão.
- Se não são muitas linhas de dados que têm um zero, e essas linhas não são teoricamente importantes, você pode decidir continuar com o log e perder algumas linhas da sua regressão.
- Em vez de utilizar log(y), tome log(y+1), de modo que zeros se tornem um e, em seguida, podem ser mantidos na regressão. Isto distorce um pouco o seu modelo e é um pouco desfavorável, mas na prática, seus efeitos colaterais negativos são tipicamente bem menores.
Melhorando seu modelo: variáveis ausentes
Provavelmente a razão mais comum de um modelo não se ajustar é que nem todas as variáveis corretas estão incluídas. Esse problema em particular tem muitas soluções possíveis.
Adição de uma nova variável
Às vezes, a correção é tão fácil quanto adicionar outra variável ao modelo. Por exemplo, se o movimento na barraca de limonada for muito maior nos fins de semana do que durante a semana, seu diagrama previsto vs. real pode ter o seguinte aspecto (coeficiente de determinação de 0,053), uma vez que o modelo está pegando apenas a média de dias de fim de semana e dias da semana:
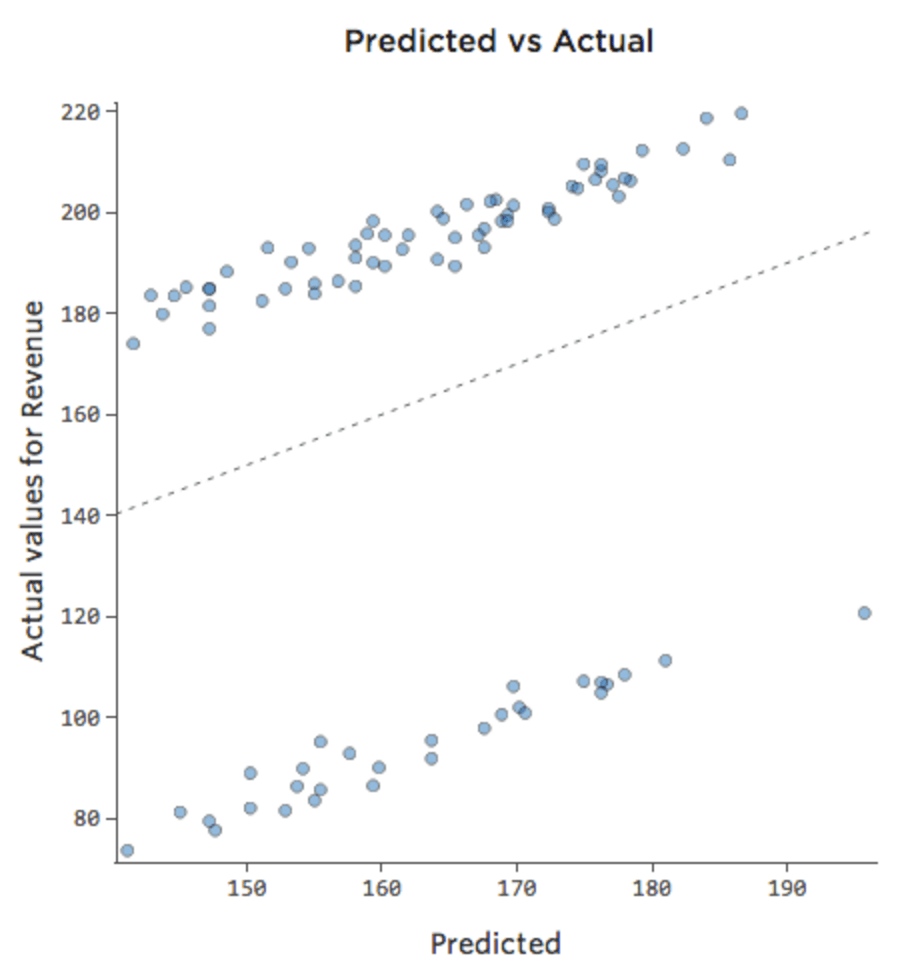
Se o modelo incluir uma variável chamada “Final de semana”, então o diagrama previsto vs. real pode ter o seguinte aspecto (coeficiente de determinação de 0,974):
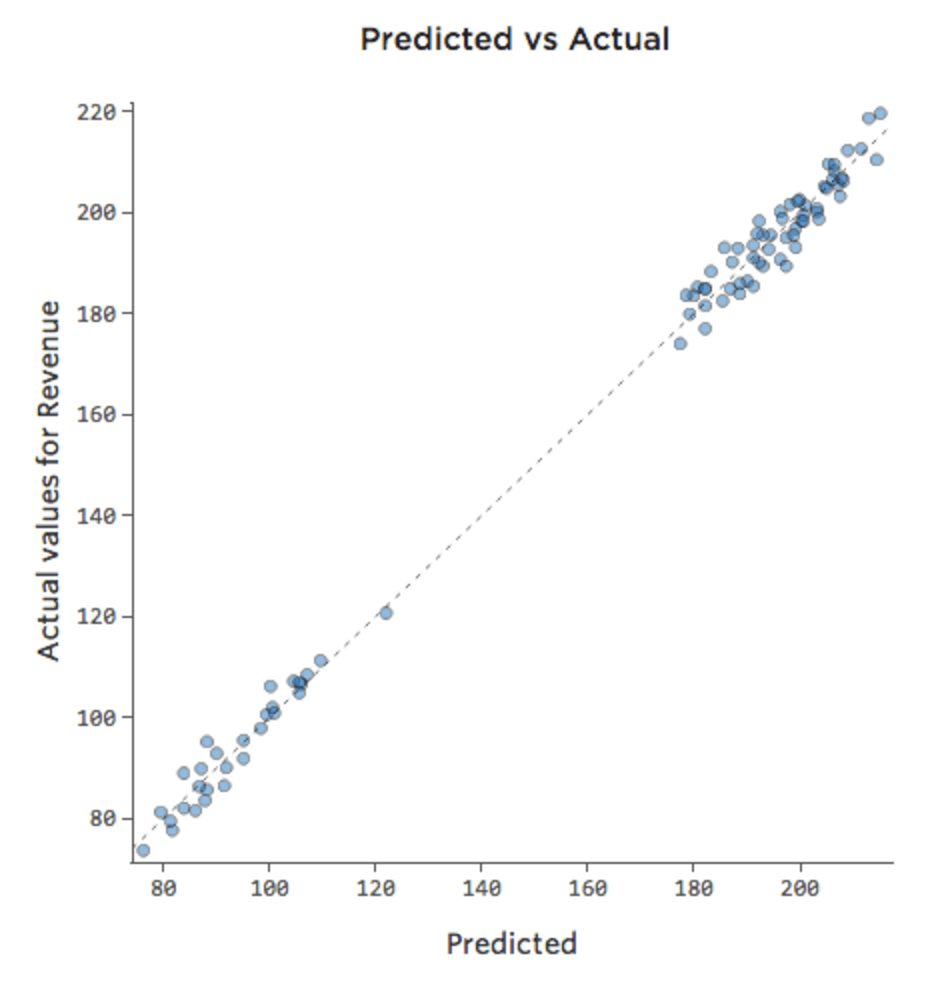
O modelo faz previsões muito mais precisas porque consegue levar em conta se um dia da semana é um dia da semana ou não.
Observe que, às vezes, você precisará criar variáveis no Stats iQ para melhorar seu modelo dessa forma. Por exemplo, você pode ter tido uma variável “Data” (com valores como “26/10/2014”) e pode precisar criar uma nova variável chamada “Dia da semana” (ou seja, domingo) ou fim de semana (ou seja, fim de semana).
Variável omitida indisponível
Mas raramente é assim tão fácil. Muitas vezes, a variável relevante não está disponível porque você não sabe o que é ou foi difícil coletar. Talvez não fosse uma questão de fim de semana vs. dia da semana, mas algo como “Número de concorrentes na área” que você não conseguiu coletar na hora.
Se a variável de que você precisa está indisponível, ou você nem sabe o que seria, então seu modelo não pode ser realmente melhorado e você tem que avaliá-la e decidir o quão feliz você está com ela (seja útil ou não, mesmo que seja falha).
Interações entre variáveis
Talvez nos finais de semana a barraca de limonada esteja sempre vendendo a 100% da capacidade, portanto independente da “Temperatura”, a “Receita” é alta. Mas nos dias de semana, a barraca de limonada é muito menos movimentada, então “Temperatura” é um importante condutor da “Receita”. Se você executou uma regressão que incluía “Fim de semana” e “Temperatura”, poderá ver um diagrama previsto vs. real como este, em que a linha ao longo do topo são os dias de fim de semana.
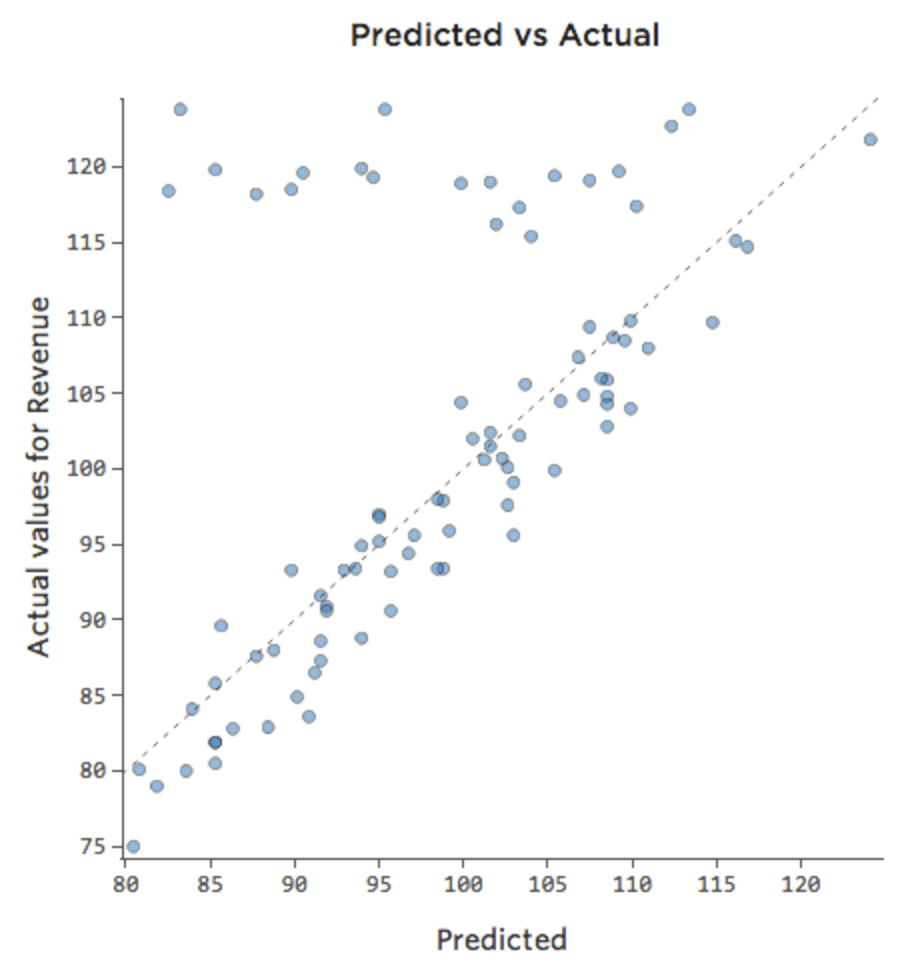
Nós diríamos que há uma interação entre “Fim de semana” e “Temperatura”; o efeito de um deles sobre “Receita” é diferente com base no valor do outro. Se criarmos uma variável de interação, obtemos um modelo muito melhor, em que previsto vs. real tem a seguinte aparência:
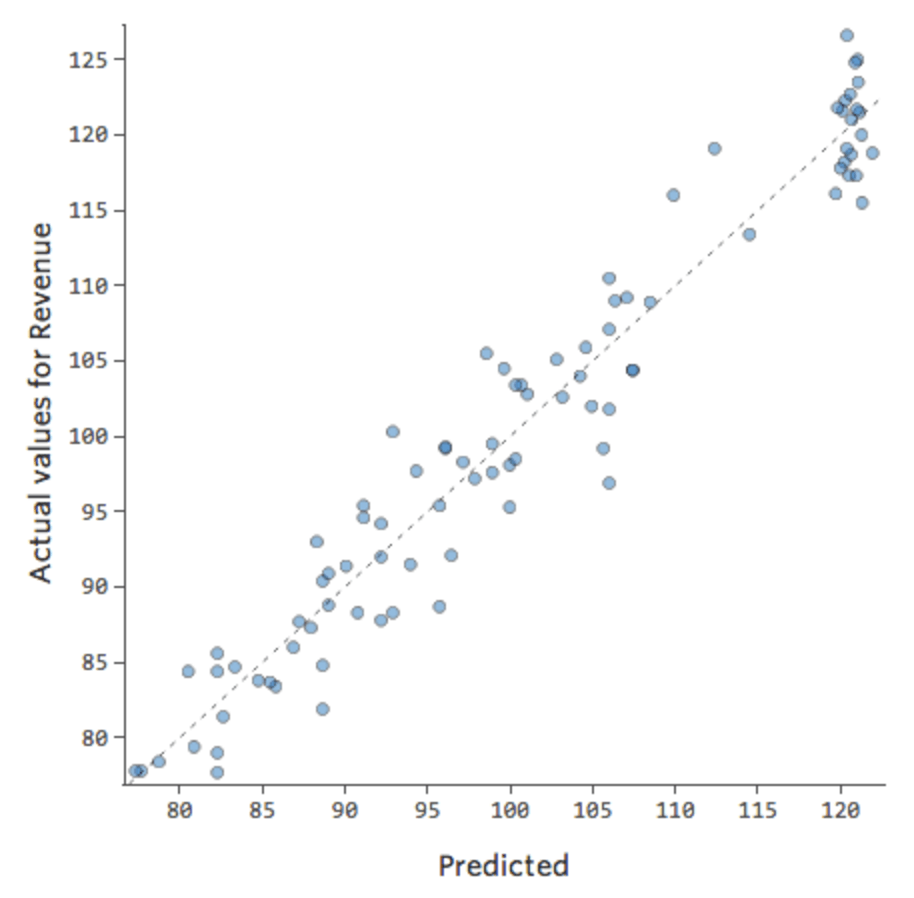
Melhorando seu modelo: corrigindo a não linearidade
Digamos que você tem uma relação que se parece com isto:
Você pode notar que a forma é a de uma parábola, a qual você pode recordar está normalmente associada a fórmulas que têm o seguinte aspecto:
y = x2 + x + 1
Por padrão, a regressão usa um modelo linear assim:
y = x + 1
Na verdade, a linha no gráfico acima tem esta fórmula:
y = 1,7x + 51
Mas é um péssimo ajuste. Assim, se adicionarmos um termo x2 , nosso modelo tem uma melhor chance de encaixar-se na curva. Na verdade, ele cria o seguinte:
A fórmula para essa curva é:
y = -2x2 +111x – 1408
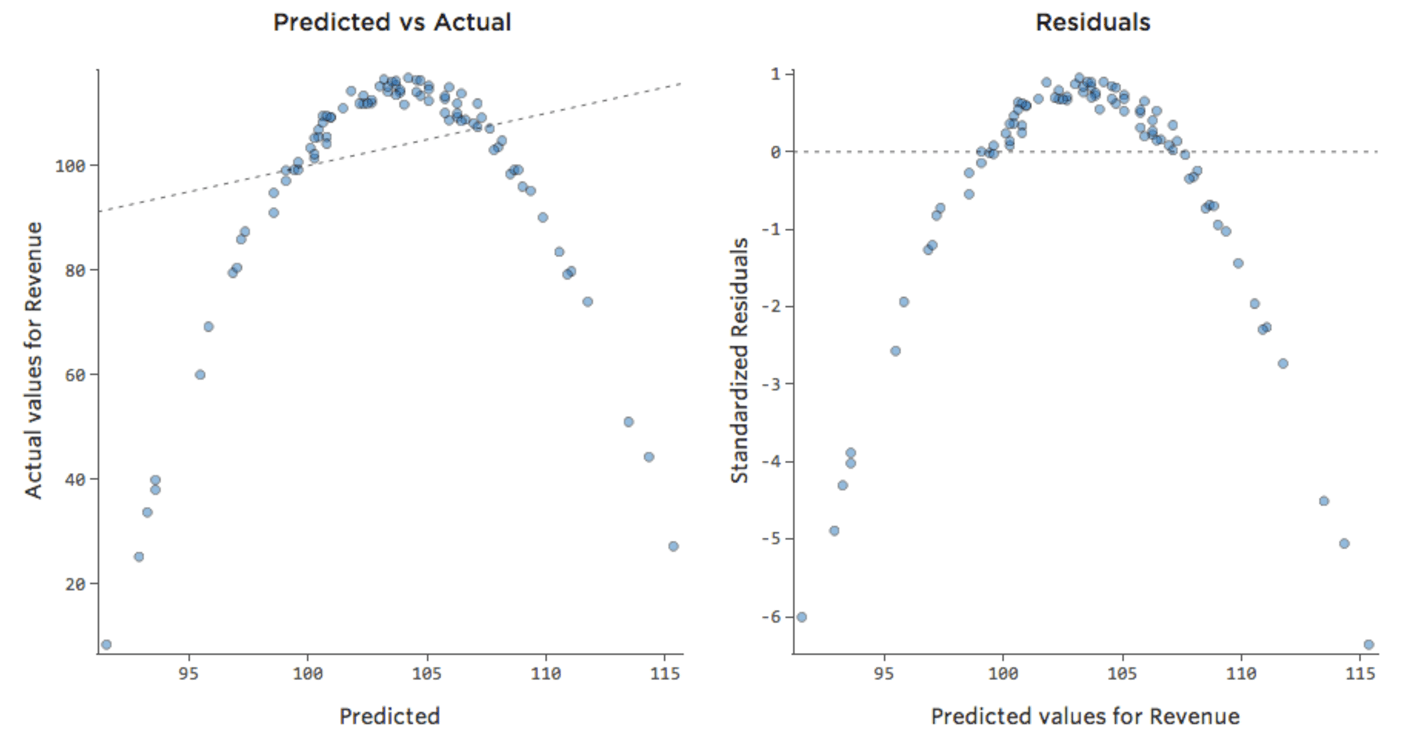
Isso significa que nossos gráficos de diagnóstico mudam a partir disso…
…para isto:
Note-se que estes são gráficos de diagnóstico saudáveis, embora os dados pareçam estar desequilibrados para o lado direito.
O método acima pode ser estendido para outros tipos de formas, particularmente uma curva em forma de S, adicionando um termo x3. No entanto, isso é relativamente incomum.
Alguns cuidados:
- De um modo geral, se você tiver um termo x2 devido a um modelo não linear em seus dados, você quer ter um termo simples-antigo-x-não-x2 . Você pode achar que seu modelo é perfeitamente bom sem ele, mas você deve definitivamente tentar ambos para começar.
- A equação de regressão pode ser de difícil compreensão. Para a equação linear no início desta seção, para cada unidade adicional de “Temperatura“, “Receita” subiu 1,7 unidades. Quando você tem x2 e x na equação, não é fácil dizer “Quando a temperatura sobe um grau, aqui está o que acontece”. Às vezes, por essa razão, é mais fácil usar apenas uma equação linear, assumindo que a equação se encaixa bem o suficiente.