A Matriz confusão e a troca entre precisão e recall
A matriz de confusão e o gráfico de precisão-recall o ajudam a avaliar a precisão do modelo.
Matriz de confusão
Digamos que você esteja pensando em dar um cubo de açúcar extra aos clientes que provavelmente retornarão. Mas é claro que você quer evitar distribuir cubos de açúcar desnecessariamente, então você só os dá aos clientes que o modelo diz que têm pelo menos 30% de probabilidade de retornar.
Se alguns clientes novos passassem por você..
| ID do cliente | Idade | Sexo |
|---|---|---|
| … | … | … |
| 324 | 54 | Feminino |
| 325 | 23 | Feminino |
| 326 | 62 | Masculino |
| 327 | 15 | Feminino |
| … | … | … |
…você poderia usar nosso modelo de regressão para prever a probabilidade de eles retornarem..
| ID do cliente | Idade | Sexo | Probabilidade de retorno estimada pelo modelo |
|---|---|---|---|
| … | … | … | … |
| 324 | 54 | Feminino | 34% |
| 325 | 23 | Feminino | 24% |
| 326 | 62 | Masculino | 65% |
| 327 | 15 | Feminino | 7% |
| … | … | … | … |
…e decidir classificar os clientes com pelo menos 30% de probabilidade como “Voltarão” e dar a eles cubos de açúcar:
| ID do cliente | Idade | Sexo | Probabilidade de retorno estimada pelo modelo | Previsão do modelo (corte de 30%) |
|---|---|---|---|---|
| … | … | … | … | … |
| 324 | 54 | Feminino | 34% | Retornará |
| 325 | 23 | Feminino | 24% | Não vai |
| 326 | 62 | Masculino | 65% | Retornará |
| 327 | 15 | Feminino | 7% | Não vai |
| … | … | … | … | … |
Para entender melhor a precisão do nosso modelo, no entanto, você pode aplicar aos pontos de dados que já possui, nos quais você já sabe se o cliente retornou..
| ID do cliente | Idade | Sexo | Probabilidade de retorno estimada pelo modelo | Previsão do modelo (corte de 30%) |
Devolvido |
|---|---|---|---|---|---|
| 1 | 21 | Masculino | 44% | Retornará | Devolvido |
| 2 | 34 | Feminino | 4% | Não vai | Devolvido |
| 3 | 13 | Feminino | 65% | Retornará | Não foi |
| 4 | 25 | Feminino | 27% | Não vai | Não foi |
| … | … | … | … | … | … |
…e avaliar a precisão dos dados..
| ID do cliente | Idade | Sexo | Probabilidade de retorno estimada pelo modelo | Previsão do modelo (corte de 30%) |
Devolvido | Precisão da previsão |
|---|---|---|---|---|---|---|
| 1 | 21 | Masculino | 44% | Retornará | Devolvido | Correto |
| 2 | 34 | Feminino | 4% | Não vai | Devolvido | Incorreto |
| 3 | 13 | Feminino | 65% | Retornará | Não foi | Incorreto |
| 4 | 25 | Feminino | 27% | Não vai | Não foi | Correto |
| … | … | … | … | … | … | … |
…e depois dividi-lo nas seguintes categorias:
- Verdadeiro positivo: Classificado pelo modelo como “Retornará” e de fato “Retornou” na realidade.
- Falso positivo: Classificado pelo modelo como “Retornará”, mas, na realidade, “Não retornou”.
- Verdadeiro negativo: Classificado pelo modelo como “Não retornará” e, na realidade, “Não retornou”.
- Falso negativo: Classificado pelo modelo como “Não retornará”, mas na realidade “Retornou”.
| ID do cliente | Idade | Sexo | Probabilidade de retorno estimada pelo modelo | Previsão do modelo (corte de 30%) |
Devolvido | Precisão da previsão | Tipo de precisão |
|---|---|---|---|---|---|---|---|
| 1 | 21 | Masculino | .44 | Retornará | Devolvido | Correto | Verdadeiro positivo |
| 2 | 34 | Feminino | .04 | Não vai | Devolvido | Incorreto | Falso negativo |
| 3 | 13 | Feminino | .65 | Retornará | Não foi | Incorreto | Falso positivo |
| 4 | 25 | Feminino | .27 | Não vai | Não foi | Correto | Verdadeiro negativo |
| … | … | … | … | … | … | … | … |
Por fim, você poderia resumir todo esse trabalho em precisão e recuperação.
Precisão:
- Dos que foram classificados como “Voltarão”, que proporção realmente voltou?
- Verdadeiro positivo / (Verdadeiro positivo + Falso positivo)
Recall:
- Lembre-se: Das pessoas que de fato “retornaram”, que proporção foi classificada dessa forma?
- Verdadeiro positivo / (Verdadeiro positivo + Falso negativo)
Modelos melhores têm valores mais altos para precisão e recuperação.
- Você pode imaginar um modelo com 94% de precisão (quase todos os identificados como “Voltarão” de fato voltam) e 97% de recuperação (quase todos os que “Voltaram” foram identificados como tal).
- Um modelo mais fraco pode ter 95% de precisão, mas 50% de recuperação (quando identifica alguém como “Retornará”, está amplamente correto, mas rotula erroneamente como “Não retornará” metade das pessoas que de fato “Retornaram” posteriormente).
- Ou talvez o modelo tenha 60% de precisão e 60% de recuperação.
Esses números devem lhe dar uma boa noção da precisão do seu modelo, mesmo que você não queira fazer nenhuma previsão.
Precisão vs. Curva de recall
Em qualquer modelo, você também pode decidir enfatizar a precisão ou a recuperação. Talvez você tenha poucos cubos de açúcar e queira distribuí-los apenas para pessoas que você tem certeza de que retornarão, então você decide distribuí-los apenas para clientes que têm 60% de probabilidade de retornar (em vez de 30%).
Nossa precisão aumentará porque você só distribuirá cubos de açúcar quando estiver realmente confiante de que alguém “voltará” Nosso recall diminuirá porque haverá muitas pessoas que acabarão “retornando” e para as quais você não estava confiante o suficiente para dar um cubo de açúcar.
Precisão: 62% -> 80%Recall
:
60% -> 30%Ou
, se você estiver se sentindo rico em cubos de açúcar, poderá distribuí-los a qualquer pessoa com pelo menos 10% de chance de ser um retornador.
Precisão: 62% -> 40%Recall
:
60% -> 90%Você
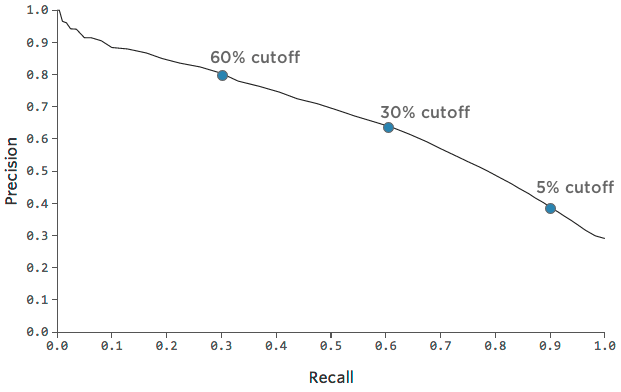
pode rastrear essa troca entre precisão e recuperação com este gráfico:
Pode ser útil escolher um ponto no gráfico que represente uma boa combinação de precisão e recuperação e, em seguida, ter uma noção de quão preciso é o modelo nesse ponto.