Análise de correspondência (BX)

Sobre a análise de correspondência

A análise de correspondência revela as relações relativas entre e dentro de dois grupos de variáveis, com base em dados fornecidos em uma tabela de contingência. Para percepções da marca, estes dois grupos são:

1. Marcas
2. Atributos que se aplicam a essas marcas

Por exemplo, digamos que uma empresa quer saber quais atributos os consumidores associam a diferentes marcas de produtos de bebidas. A análise de correspondência ajuda a medir semelhanças entre marcas e a força das marcas em termos de suas relações com diferentes atributos. Entender as relações relativas permite que os donos das marcas identifiquem os efeitos de ações anteriores em diferentes atributos relacionados à marca e decidam as próximas etapas a serem executadas.

A análise de correspondência é valiosa nas percepções da marca por alguns motivos. Ao tentar observar relações relativas entre marcas e atributos, o tamanho da marca pode ter um efeito enganoso; a análise de correspondência remove esse efeito. A análise de correspondência também oferece uma visão rápida intuitiva das relações de atributo de marca (com base na proximidade e na distância da origem) que não é fornecida por muitos outros gráficos.

Nesta página, explicaremos um exemplo de como aplicar a análise de correspondência a um caso de uso de diferentes marcas (fictícias) de produtos de refrigerantes.

Vamos começar com o formato de dados de entrada – uma tabela de contingência.

Tabelas de contingência

Uma tabela de contingência é uma tabela bidimensional com grupos de variáveis nas linhas e colunas. Se nossos grupos, como descrito acima, fossem marcas e seus atributos associados, executaríamos pesquisas e retornaríamos diferentes contagens de respostas associando diferentes marcas aos atributos indicados. Cada célula na tabela representa o número de respostas ou contagens que associam esse atributo a essa marca. Essa “associação” seria exibida por meio de uma pergunta de pesquisa, como “Escolher marcas de uma lista abaixo da qual você acredita que mostra o atributo ___”.

Aqui, os dois grupos são “marcas” (linhas) e “atributos” (colunas). A célula no canto inferior direito representa a contagem de respostas para a marca “Brawndo” e o atributo “Econômico”.

Resíduos (R)

Na análise de correspondência, queremos ver os resíduos de cada célula. Um resíduo quantifica a diferença entre os dados observados e os dados que esperaríamos – assumindo que não há relação entre as categorias de linha e coluna (aqui, essas seriam marca e atributo). Um resíduo positivo nos mostra que a contagem para esse pareamento de atributos de marca é muito superior ao esperado, sugerindo uma relação forte; correspondentemente, um resíduo negativo apresenta um valor inferior ao esperado, sugerindo uma relação mais fraca. Vamos percorrer o cálculo desses resíduos.

Um resíduo (R) é igual a: R = P – E, onde P é as proporções observadas e E é as proporções esperadas para cada célula.  Vamos detalhar essas proporções observadas e esperadas!

Proporções observadas (P)

Uma proporção observada (P) é igual ao valor em uma célula dividido pela soma total de todos os valores na tabela. Assim, para nossa tabela de contingência acima, a soma total seria: 5 + 7 + 2 + 18 … + 16 = 312. Dividir o valor de cada célula pelo total de resultados na tabela abaixo para proporções observadas (P).

Por exemplo, na célula inferior direita, tomamos o valor inicial da célula de 16/312 = 0,051. Isso nos diz a proporção de todo o nosso gráfico que o emparelhamento de Brawndo e Economic representa com base em nossos dados coletados.

Massas de linhas e colunas

Algo que podemos calcular facilmente a partir de nossas proporções observadas, e será usado muito depois, são as somas das linhas e colunas de nossa tabela de proporções, que são conhecidas como as massas de linha e coluna. Uma massa de linha ou coluna é a proporção de valores para essa linha/coluna. A massa da linha para “Butterbeer”, olhando para nosso gráfico acima, seria 0,016 + 0,022 + 0,006, nos dando 0,044.

Fazendo cálculos semelhantes, acabamos com:

Proporções previstas (E)

Proporções esperadas (E) seriam o que esperávamos ver na proporção de cada célula, assumindo que não há relação entre linhas e colunas. Nosso valor esperado para uma célula seria a massa da linha dessa célula multiplicada pela massa da coluna daquela célula.

Veja na célula superior esquerda, a massa da linha para Butterbeer multiplicada pela massa da coluna para Tasty, 0,044 * 0,182 = 0,008.

Agora podemos calcular nossa tabela de resíduos (R), onde R = P – E. Os resíduos quantificam a diferença entre as proporções dos nossos dados observados e as proporções esperadas dos nossos dados, se assumirmos que não há relação entre as linhas e colunas.

Tomando o nosso valor mais negativo de -0,045 para Squishee e Econômico, o que interpretaríamos aqui é que há uma associação negativa entre Squishee e Econômico; Squishee é muito menos provável de ser visto como “Econômico” do que nossas outras marcas de bebidas.

Resíduos indexados (I)

No entanto, há alguns problemas com apenas a leitura de resíduos.

Observando a linha superior da tabela de cálculo de resíduos acima, vemos que todos esses números estão muito próximos de zero. Não devemos tirar a óbvia conclusão disso de que a Butterbeer não está relacionada com nossos atributos, pois essa suposição é incorreta. A explicação real seria que as proporções observadas (P) e as proporções esperadas (E) são pequenas porque, como a nossa massa de fileira nos diz, apenas 4,4% da amostra são Butterbeer.

Isso levanta um grande problema ao olhar para os resíduos, na medida em que, por desconsiderarmos o número real de registros nas linhas e colunas, nossos resultados são desviados para as linhas/colunas com massas maiores. Podemos corrigir isso dividindo nossos resíduos por nossas proporções esperadas (E), nos dando uma tabela de nossos resíduos indexados (I, I = R / E):

Os resíduos indexados são de fácil interpretação: quanto maior o valor da tabela, maior a proporção observada em relação à proporção esperada.

Por exemplo, tomando o maior valor à esquerda, a Butterbeer tem 95% mais probabilidade de ser vista como “Tasty” do que o que esperávamos se não houvesse relação entre essas marcas e atributos. Enquanto que no valor mais alto da direita, a Butterbeer tem 65% menos probabilidade de ser vista como “Econômica” do que o que esperávamos – sem nenhuma relação entre nossas marcas e atributos.

Tendo em vista nossos resíduos indexados (I), nossas proporções esperadas (E), nossas proporções observadas (P) e nossas massas de linhas e colunas, vamos calcular nossos valores de análise de correspondência para nosso gráfico!

Cálculo de coordenadas para análise de correspondência

Decomposição de valor singular (SVD)

Nosso primeiro passo é calcular a decomposição do valor singular, ou SVD. O SVD nos fornece valores para calcular o desvio e traçar nossas linhas e colunas (marcas e atributos).

Calculamos a SVD no resíduo padronizado (Z), onde Z = I * sqrt(E), onde I é o nosso resíduo indexado, e E é a nossa proporção esperada. A multiplicação por E faz com que nossa SVD seja ponderada, de modo que células com maior valor esperado recebem um peso maior, e vice-versa, o que significa que, como os valores esperados estão frequentemente relacionados ao tamanho da amostra, células “menores” na tabela, onde o erro amostral teria sido maior, são minimizadas. Assim, a análise de correspondência utilizando uma tabela de contingência é relativamente robusta para anomalias causadas por erro de amostragem.

Voltando ao SVD, temos: SVD = svd(Z). Uma decomposição de valor singular gera 3 saídas:

Um vetor, d, contendo os valores singulares.

Uma matriz, u, contendo os vetores singulares à esquerda (marcas).

Uma matriz, v, contendo os vetores singulares à direita (atributos).

Os vetores singulares à esquerda correspondem às categorias nas linhas da tabela, e os vetores singulares à direita correspondem às colunas. Cada um dos valores singulares, para o cálculo da variância, e os vetores correspondentes (ou seja, colunas de u e v), para plotar posições, correspondem a uma dimensão. As coordenadas utilizadas para plotar categorias de linha e coluna para nosso gráfico de análise de correspondência são derivadas das duas primeiras dimensões.

Variância expressa por nossas dimensões

Os valores singulares quadrados são conhecidos como autovalores (d^2). Os autovalores em nosso exemplo são 0,0704, 0,0129 e 0,0000. Exprimindo cada autovalor como uma proporção da soma total nos diz a quantidade de variância capturada em cada dimensão de nossa análise de correspondência, com base no valor singular de cada dimensão; obtemos 84,5% de variância expressa por nossa primeira dimensão, e 15,5% em nossa segunda dimensão (nossa terceira dimensão explica 0% da variância).

Análise de correspondência padrão

Agora estamos equipados com os recursos para calcular a forma básica de análise de correspondência, usando o que são conhecidos como coordenadas padrão, calculadas a partir de nossos vetores singulares esquerdo e direito. Anteriormente, ponderávamos os resíduos indexados antes da realização do SVD. Para obter coordenadas que representam nossos resíduos indexados, precisamos agora desponderar as saídas de SVD, dividindo cada linha dos vetores singulares esquerdos pela raiz quadrada das massas da linha, e dividindo cada coluna dos vetores singulares direitos pela raiz quadrada das massas da coluna, obtendo-nos as coordenadas padrão das linhas e colunas para plotagem.

Coordenadas padrão da marca:

Atributo Coordenadas padrão:

Utilizamos as duas dimensões com a maior variância capturada para plotagem, a primeira dimensão indo para o eixo X e a segunda dimensão no eixo Y, gerando nosso gráfico de análise de correspondência padrão.

Estabelecemos a base dos cálculos necessários para a análise de correspondência padrão. Na próxima seção, exploraremos os prós e contras de diferentes estilos de análise de correspondência e que melhor se adequa aos nossos propósitos de ajudar na análise das percepções da marca.

Tipos de análise de correspondência

Análise correspondência principal linha/coluna

A análise de correspondência padrão é fácil de calcular e resultados fortes podem ser obtidos a partir dela. No entanto, a correspondência padrão é uma má escolha para nossas necessidades; as distâncias entre as coordenadas da linha e da coluna são exageradas, e não há uma interpretação direta das relações entre as categorias de linha e coluna. O que queremos para interpretar relações entre coordenadas de linha (marca) e interpretar relações entre categorias de linha e coluna é a normalização principal de linha (ou, se nossas marcas estavam em nossas colunas, normalização principal de coluna).

Para a normalização do principal da linha, você deseja utilizar as coordenadas padrão calculadas acima para seus valores de coluna (atributo), mas deseja calcular as coordenadas principais para seus valores de linha (marca). O cálculo das coordenadas principais é tão simples quanto tomar as coordenadas padrão, e multiplicá-las por seus correspondentes valores singulares (d). Portanto, para nossas linhas, queremos apenas multiplicar nossas coordenadas de linha padrão por nossos valores singulares (d), mostrados na tabela abaixo. Para a normalização principal da coluna, nós simplesmente multiplicamos nossas colunas em vez de nossas linhas por nossos valores singulares (d).

Substituindo em nossas coordenadas principais para nossas linhas (marcas), acabamos com:

Porque nós escalamos por nossos valores singulares, nossas coordenadas principais para nossas linhas representam a distância entre os perfis de linha de nossa tabela original; pode-se interpretar as relações entre nossas coordenadas de linha em nosso gráfico de análise de correspondência por sua proximidade uns com os outros.

A distância entre nossas coordenadas de coluna, uma vez que são baseadas em coordenadas padrão, ainda são exageradas. Além disso, nossa escala por nossos valores singulares em apenas uma das duas categorias (linhas/colunas) nos deu uma forma de interpretar as relações entre as categorias de linha e coluna. Dado um valor de linha e um valor de coluna, por exemplo, Butterbeer (linha) e Tasty (coluna), quanto maior a sua distância à origem, mais forte é a sua associação com outros pontos no mapa. Além disso, quanto menor o ângulo entre os dois pontos (Butterbeer e Tasty), maior a correlação entre os dois.

A distância à origem combinada com o ângulo entre os dois pontos é o equivalente a tomar o produto pontual; o produto ponto entre uma linha e um valor de coluna mede a força da associação entre os dois. Na verdade, quando a primeira e a segunda dimensão explicam toda a variância nos dados (soma de 100%), o produto ponto é diretamente igual ao resíduo indexado das duas categorias. Aqui, o produto ponto seria a distância à origem dos dois pontos multiplicado pelo cosseno do ângulo entre eles; .59*2.12*cos(41) = .94. Levando em conta erros de arredondamento, é o mesmo que nosso valor residual indexado de 0,95. Assim, ângulos menores que 90 graus representam um resíduo indexado positivo e, portanto, uma associação positiva, e ângulos maiores que 90 graus representam uma associação negativa residual indexada ou negativa.

Análise de correspondência principal de linha escalonada

Analisando nosso gráfico acima para normalização principal de linhas, temos uma observação fácil – os pontos para nossas colunas (características) estão muito mais espalhados, e nossos pontos para nossas linhas (marcas) estão agrupados em torno da origem. Isso pode tornar a análise do nosso gráfico por olho muito difícil e não intuitiva, e às vezes impossível de ler as categorias de linha se todas elas estiverem sobrepostas. Felizmente, há uma maneira fácil de dimensionar nosso gráfico para trazer em nossas colunas, mantendo ainda a capacidade de utilizar o produto ponto (distância da origem e ângulo entre os pontos) para analisar as relações entre nossos pontos de linha e coluna, conhecida como normalização principal de linha escalada.

A normalização principal de linha escalonada toma a normalização principal da linha, e escala as coordenadas da coluna da mesma forma que escalamos o eixo x das coordenadas da linha – em outras palavras, nossas coordenadas de coluna são escalonadas pelo primeiro valor de nossos valores singulares (d). Nossos valores de linha permanecem iguais à normalização do principal da linha, mas agora nossas coordenadas de coluna são escalonadas para baixo por um fator constante.

Isso significa que nossas coordenadas de coluna são escalonadas para caber muito melhor com nossas coordenadas de linha, facilitando muito a análise de tendências. Como dimensionamos todas as nossas coordenadas de coluna pelo mesmo fator constante, contraímos a dispersão de nossas coordenadas de coluna no mapa, mas não fizemos nenhuma alteração em suas relatividades; ainda utilizamos o produto ponto para medir a força das associações. A única mudança é que quando nossa primeira e segunda dimensão cobrem toda a variância nos dados, em vez do residual indexado ser igual ao produto pontual das duas categorias, agora é igual ao produto pontual escalonado das duas categorias, que é o produto pontual escalonado por um valor constante do nosso primeiro valor singular (d). A interpretação do gráfico permanece a mesma que a normalização do principal da linha.

Análise de correspondência principal

Uma forma final de análise de correspondência que mencionaremos é a análise de correspondência principal, também conhecida como mapa simétrico, escalamento francês ou análise de correspondência canônica. Em vez de apenas multiplicar as linhas ou colunas padrão pelos valores singulares (d) como na análise de correspondência principal de linha/coluna, nós multiplicamos as duas pelos valores singulares. Assim, nossos valores de coluna padrão, multiplicados pelos valores singulares, se tornam:

Colocando estes em conjunto com nossos valores de linha calculados na linha de análise principal, obtemos:

A análise de correspondência canônica escala as coordenadas de linha e coluna pelos valores singulares. Isso significa que podemos interpretar nossas relações entre nossas coordenadas de linha da mesma forma como fizemos na análise de correspondência principal da linha (com base na proximidade), E podemos interpretar nossas relações entre nossas coordenadas de coluna de forma semelhante à análise de correspondência principal da coluna; podemos analisar relações entre marcas e relações entre atributos. Também perdemos o clustering de linhas/colunas no centro do mapa a partir da análise principal de linha/coluna. No entanto, o que perdemos da análise de correspondência canônica, é uma forma de interpretar relações entre nossas marcas e atributos, algo muito útil nas percepções da marca.

Comparação lado a lado

Análise de correspondência padrão

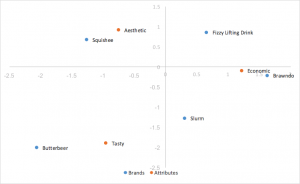
O estilo mais fácil de análise de correspondência para computar, usando vetores singulares esquerdo e direito de SVD dividido por massas de linhas e colunas. As distâncias entre as coordenadas de linha e coluna são exageradas, e não há uma interpretação direta das relações entre as categorias de linha e coluna.

Análise correspondência normalização principal linha

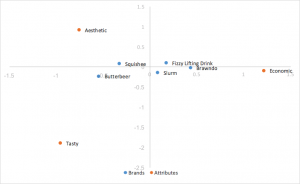
Utiliza coordenadas padrão de cima, mas multiplica as coordenadas da linha pelos valores singulares para normalizar. As relações entre linhas (marcas) são baseadas na distância umas das outras. As distâncias da coluna (atributo) ainda são exageradas. As relações entre linhas e colunas podem ser interpretadas pelo produto pontual. Linhas (marcas) tendem a ser agarradas no centro.

Análise correspondência normalização principal linha escalonada

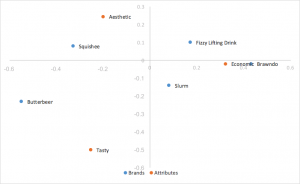
Toma a normalização principal da linha e escala as coordenadas de coluna por uma constante do primeiro valor singular. Mesmas interpretações extraídas da normalização principal da linha, substituindo o produto pontual pelo produto pontual escalonado. Ajuda a remover o agarramento de linhas no centro. Este é o estilo de análise de correspondência que preferimos.

Análise de correspondência de normalização principal (simétrico, mapa francês, canônico)

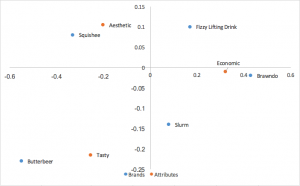
Outra forma popular de análise de correspondência usando coordenadas principais normalizadas nas linhas e colunas. As relações entre linhas (marcas) podem ser interpretadas pela distância entre si; o mesmo pode ser dito para colunas (atributos). Nenhuma interpretação pode ser desenhada para relações entre linhas e colunas.

Conclusão

Em conclusão, a análise de correspondência é utilizada para analisar as relações relativas entre e dentro de dois grupos; no nosso caso, esses grupos seriam marcas e atributos.

A análise de correspondência elimina uma distorção nos resultados de diferentes massas entre grupos, utilizando resíduos indexados. Para a normalização das percepções da marca para análise de correspondência, utilizamos a normalização do principal da linha (ou principal da coluna se as marcas são colocadas nas colunas), pois isso nos permite analisar as relações entre as diferentes marcas pela proximidade entre elas, e também permite analisar as relações entre marcas e atributos pela distância da origem combinada com o ângulo entre elas e a origem (o produto pontual), ao sacrifício de representar mal a relação entre atributos com distâncias exageradas entre eles e a origem (o produto pontual), no sacrifício de representar mal a relação entre atributos com distâncias exageradas entre nós (não importa). Utilizamos a normalização principal de linha/coluna escalonada para facilitar a análise de nosso gráfico sem nenhum custo. Queremos ter em mente que adicionamos a variância explicada a partir das etiquetas dos eixos X e Y (a primeira e a segunda dimensão) para visualizar a variância total capturada no mapa; quanto menor for esse número, mais inexplicada será a variância existente nos dados e mais enganosa será a plotagem.

Uma última coisa a lembrar é que a análise de correspondência só mostra relatividades desde que eliminamos o fator de massa de nossos dados; nosso gráfico não nos dirá nada sobre quais marcas têm as pontuações “mais altas” em atributos. Depois de entender como criar e analisar os gráficos, a análise de correspondência é uma ferramenta poderosa que desconsidera os efeitos do dimensionamento da marca para fornecer insights poderosos e fáceis de interpretar sobre as relações entre as marcas e seus atributos aplicáveis.

Perguntas frequentes