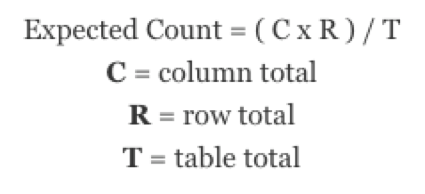-
Qualtrics Platform -
Customer Journey Optimizer -
XM Discover -
Qualtrics Social Connect
統計を理解する
統計について
クアルトリクス統計へようこそ。クアルトリクスでプロジェクトを作成・分析する際に役立つ、基本的な統計情報の概要です。基本的な統計概念をいくつか取り上げ、それをプラットフォームに適用し、クアルトリクス以外の選択肢についても説明します。
定量データとカテゴリーデータ
定量データとカテゴリーデータの2種類がある。
定量データは数値でアセスメントされる。定量データの例としては、年齢、身長、収入などがある。
カテゴリーデータは名義尺度でアセスメントする。カテゴリーデータの例としては、性別、配偶者の有無、職業などがある。アンケート調査で収集されるデータの多くはカテゴリー別であり、あるカテゴリーに該当する回答者の数をカウントする。
センターの尺度
定量データには、平均値、中央値、最頻値という3つの中心値があります。
平均値（平均）は、データがほぼ正規分布しているか、またはベルカーブのように見える場合に、中心を測る最良の尺度である。平均は、すべてのオブザベーションを合計し、オブザベーションの合計数で区切ることによって求められる。
中央値（中間値）は、データが偏っているように見える場合に、中心を示す良い尺度である。すべての観察を順番に並べると、中央値が真ん中の値になる。
モードは、データの中で最も頻繁に出現する値である。ITは平均値や中央値ほど一般的に使われていない。
スプレッドの尺度
データの広がりを測定するのに便利な統計がいくつかあります：標準偏差、分散、範囲です。
標準偏差は，それらの平均からの観察の平均距離である．平均と同様、標準偏差は、ほぼ正規分布のデータで使用されるべきである。
分散は単純に標準偏差の2乗である。
レンジは最大値と最小値の差である。
図表における統計学
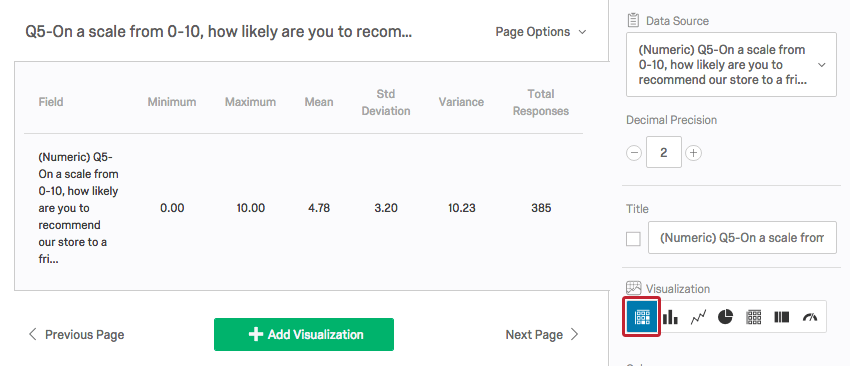
クアルトリクスの統計テーブルでは、最小値、最大値、平均、分散、標準偏差、および総回答数が表示されます。
クアルトリクスでは、すべての質問の各回答オプションに値がコード化されているため、定量データであるかカテゴリーデータであるかにかかわらず、これらの統計値を見つけることができます。これらの統計があなたの研究の文脈で意味を持つかどうかは、あなた次第である。
例えば、回答者に好きな色を尋ねることができます。赤、黄、青、緑で、それぞれ1、2、3、4とコード化します。クアルトリクスは平均値を出してくれるが、好きな色の平均値を出しても意味がない。
回答者に映画を1つ星から5つ星まで評価させた場合、平均値が役に立つだろう。星2.98や星4.32のように、映画を簡単に比較できる。
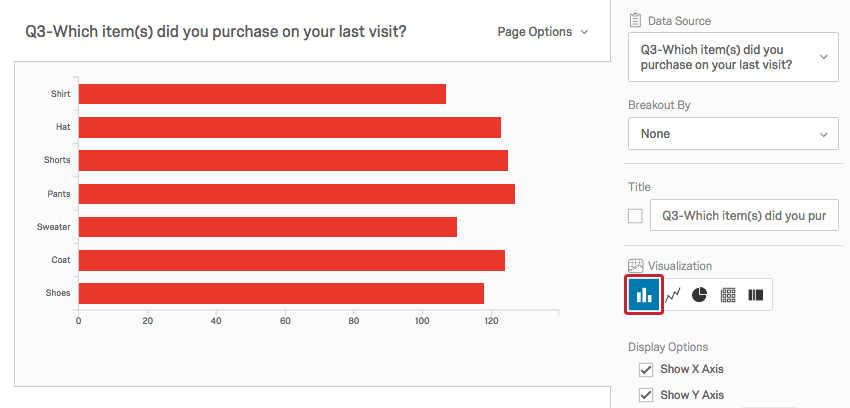
クアルトリクスには様々なチャート、グラフ、表があります。棒グラフは、各選択肢の回答頻度を示しています。
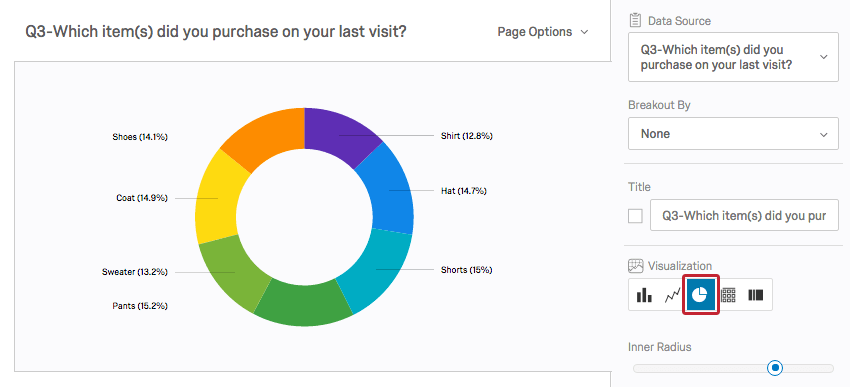
円グラフは、これらの度数をパイに占める割合で示す。
棒グラフも円グラフも、カテゴリー間の度数の比較を非常に簡単にします。
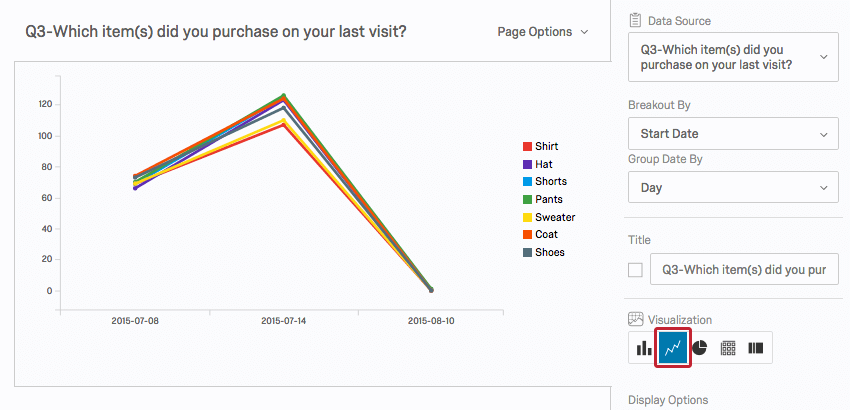
線グラフは，順序づけされたオブザベーションのための2次元散布図である．長期的なトレンドを見るには良い方法だ。
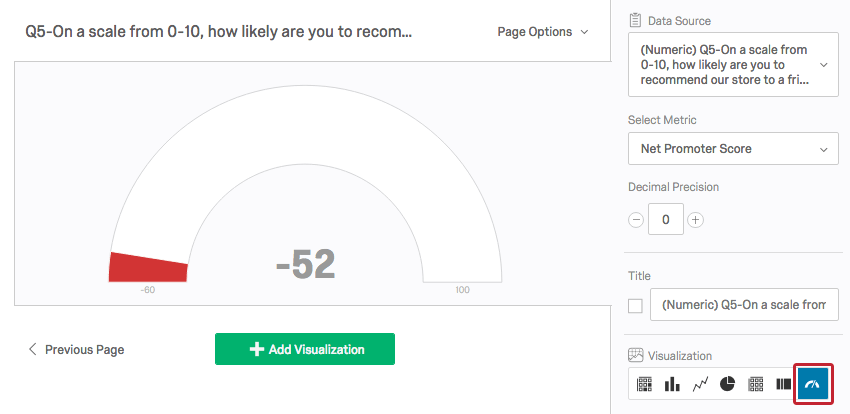
ゲージチャートは、選択した指標（平均、合計など）をスケールと比較します。その指標がどこに該当するかによって、目盛りの色が変わる。ゲージチャートは、期待されるパフォーマンスと実際のパフォーマンスを素早く比較するのに便利です。
クロス集計
カテゴリーデータを分析する1つの方法は、次のようなものである。 クロス集計分割表または2元表とも呼ばれる。クロスタブは、表のセルに記述された特定の特徴を持つ回答者の数を記録する。
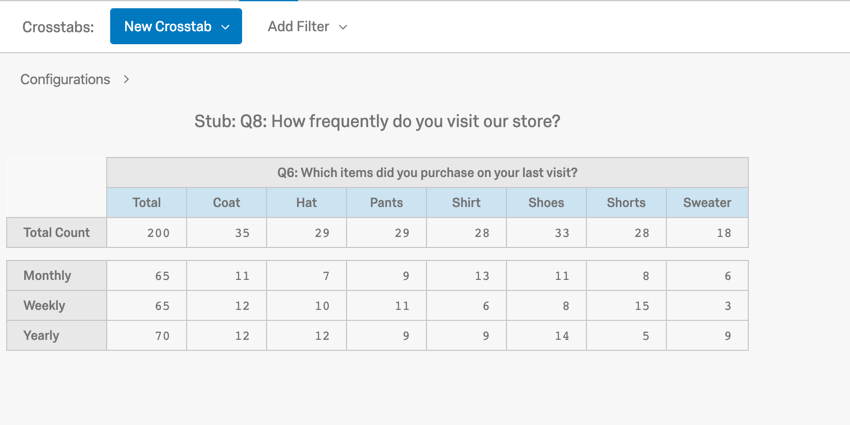
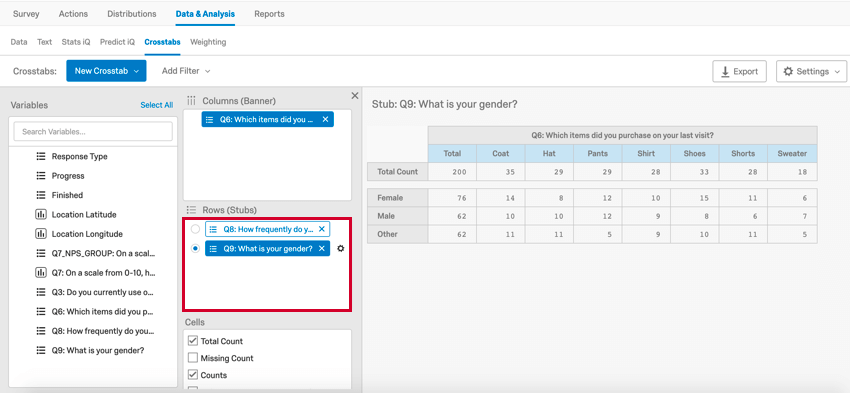
この例では、週ごと、月ごと、年ごとに購入された品目の数が表示されます（例：毎月11着のコートを購入）。
クロスタブは、それぞれ列と行、またはバナーとスタブで構成され、各バナーとスタブは質問から頻度データを取り込む。クアルトリクスでは、クロス集計に対応した質問のみを選択することができます（例えば、自由記述の質問はクロス集計に対応していません）。複数のバナーや半券を選択した場合、クロスタブエディターで表示したいバナーや半券をクリックして選択することができます。クロス集計にマルチレベルのドリルダウンを追加すると、ある変数が別の変数のサブカテゴリとして表示されます。
カイ二乗検定統計量
カイ二乗検定統計量は、半券とバナーの間の有意な関係を検定する。
複数の半券とバナーをクロスタブに含めると、クアルトリクスは複数のカイ二乗値（バナーと半券の組み合わせごとに1）を生成します。
カイ二乗検定の統計量がどのように計算されるかを知っておくことは有益である。まず、各セルの期待カウント、つまり行の合計、列の合計、表の合計に基づいて、そのセルが持つと予想されるカウントを求める必要がある。期待カウントを求めるには、行の合計に列の合計を掛け、結果をテーブルの合計で割る。
予想カウントを得たら、以下の計算を行う：
カイ2乗検定統計量は、観察値から期待値を引いた値を取り、この差を2乗し、各セルの期待値で区切ることによって求められる。そして、これらの個々のカイ2乗検定成分が合計され、その結果がカイ2乗検定統計量となる。そしてカイ2乗値は、変数間の関係が統計的に有意であるかどうかを決定するために使用されます。
P値
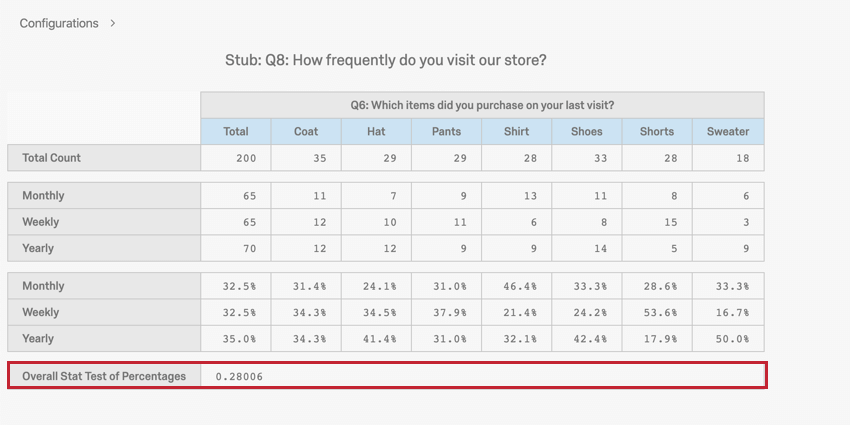
カイ2乗検定の統計量は、信頼水準とともにP値を求めるために使用される。P値は、2変数の間の関連が統計的に有意であるかどうかを決定する。低いP値は、観察された表の関係が非常に低い確率で起こることを意味し、2つの変数の間に有意な関係があることを意味する。P値が低いとは、一般的に0.05未満であると考えられている。
P値は0.28で有意ではない。したがって、来店頻度と購入商品の種類に関係はない。
追加分析
相関や回帰のような定量データのさらなる分析は、Excelや統計ソフトウェアパッケージで行うことができる。
相関関係
相関係数 r は、2 つの量的変数の間のほぼ直線的な関係の強さと方向を表す。rの値は常に-1と1の間にあり、-1と1に近い値は強い相関を表し、ゼロに近い値は弱い相関を表す。プラスまたはマイナスの記号は、関係のプラスまたはマイナスの方向を示す。.3～0.3の相関値はかなり低いと考えられ、0.7～1または-.7～-1の相関値は高いと考えられる。
覚えておくべき重要なポイントは、相関関係は因果関係と同じではないということだ。2つの変数に高い相関があるからといって、そのうちの1つの変数がもう1つの変数の発生を引き起こすとは限らない。
回帰分析
回帰分析は、1つ以上の予測変数に基づいて1つの変数の予測を行うために使用できる。リグレッションに関するヘルプは以下のページを参照：