ロジスティック回帰の使いやすいガイド
ロジスティック回帰とは何か?
ロジスティック回帰は、1つ以上の入力変数を1つの出力変数に関係付ける数式を推定する。
例えば、あなたがレモネード屋台を経営していて、どのようなタイプの客がリピーターになりやすいかに興味があるとする。あなたのデータには、各顧客の項目、最初の購入、次へレモネードを買いに来たかどうかが含まれます。あなたのデータはこのようになるかもしれない:
| 戻る | 顧客年齢 | セックス | 初回購入時の気温 | レモネード色 | パンツ丈 |
|---|---|---|---|---|---|
| そうではない | 21 | 男性 | 24 | ピンク | ショートパンツ |
| 返品 | 34 | 女性 | 20 | 黄 | ショートパンツ |
| 返品 | 13 | 女性 | 25 | ピンク | パンツ |
| そうではない | 25 | 女性 | 27 | 黄 | ドレス |
| その他 | その他 | その他 | その他 | その他 | その他 |
あなたは、”顧客年齢”(入力または説明変数)が “返品”(出力または回答変数)に影響するかもしれないと考えています。ロジスティック回帰の結果は次の
ようになる:12歳(最も低い年齢)では、「返品」される可能性は10%である。
年齢が1歳増えるごとに、”復帰 “は1.1倍になる。
このちょっとした知識が役に立つ理由は2つある。
まず、関係性を理解することができます:高齢の顧客はよりリピーターになる可能性が高い。このインサイトによって、リピーターになる可能性が高い年配の顧客に向けて広告を出すことができるかもしれない。
第二に、それに関連して、ITは具体的な予測を立てるのにも役立つ。もし24歳の客が通りかかったら、彼らがレモネードを買ったら、その後リピーターになる確率は26%だと推測できる。
確率の掛け算を理解する
確率は1:9で、1/(1+9)=10%とも書く。
のオッズ」(1)は1.5倍される。
現在は1.5:9で、1.5/(1.5+9)=14%とも表記される。
確率は1:1で、1/(1+1)=50%とも書く。
のオッズ」(並列の1)は3倍される。
現在、3:1は3/(3+1)=75%とも表記される。
それでは、この回帰モデルを作成するプロセスを説明しよう。
回帰モデルを作成する準備
1.回帰の理論をよく考えよう。
回答変数「回答収入」を選んだら、様々なインプットがITとどのように関連しているか仮説を立てます。例えば、「初回購入時の温度」が高ければ「返品」される可能性が高くなると考えるかもしれないし、「年齢」が「返品」に どう影響するかわからないかもしれないし、「パンツ」 (xml)は「温度」の影響を受けるが、レモネードスタンドには何の影響もないと考えるかもしれない。
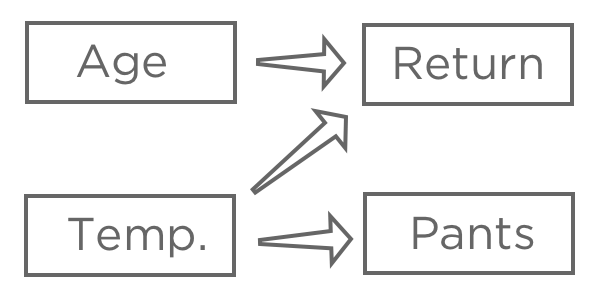
回帰の目的は通常、複数の入力と1つの出力の関係を理解することであり、この場合、おそらく「気温」、「年齢」 (「気温と年齢からリターンを予測する」とも言う、、実際の予測よりも説明に興味がある場合でも)を用いて「リターン」を説明するモデルを作成することになるでしょう。
おそらく「パンツ」は回帰に含めないだろう。どちらも「気温」に関係しているので、「帰還」と相関があるかもしれないが、因果関係の連鎖の中では「帰還」の前に来るものではないので、それを含めるとモデルが混乱してしまう。
2.あなたのモデルに少しでも役立ちそうなすべての変数を「記述」する。
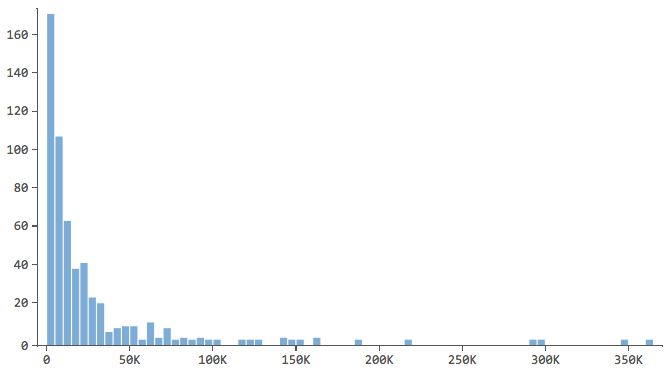
回答変数(この場合は「回答収益」)を説明し、その感触をつかむことから始めます。説明変数についても同様にしてください。
…ほとんどのデータがヒストグラムの最初の数ビンにある。これらの変数には、後で特別な注意を払う必要がある。
3.可能な説明変数をすべて応答変数に “関連づける”。
Stats iQは、結果を統計的関係の強さ順に並べます。どの変数がどのように「収益」と関連しているかに注目しながら、見た目と操作性を確かめてください。
4.リグレッションの構築を開始する。
回帰モデルの構築は反復プロセスである。以下の3段階を必要なだけ繰り返す。
回帰モデル構築の3つの段階
ステージ 1: 変数を加算または減算する。
前回の分析で「収入」 と関係があると示された変数を、ひとつずつ追加していく(または、追加する理論的な理由がある変数を追加する)。1つ1つ確認することは厳密には必要ではないが、確認しながら問題を修正することが容易になり、モデルの感覚をつかむのに役立つ。
例えば、”収益 “を “気温 “で予測することから始めるとしよう。強力な関係を見つけ、モデルをアセスメントし、満足のいくものであると判断する(詳細は後ほど)。
Return <- Temperature
次に「レモネードの色」を加えると、回帰モデルには2つの項ができ、どちらも統計的に有意な予測因子となる。このように、”
Revenue <- Temperature & Lemonade color
“を追加すると、モデルの結果、”Sex “は統計的に有意であるが、”Lemonade color “は有意でなくなる。一般的には、モデルから “レモネードカラー “を削除する。
つまり
、客の性別がわかっても、注文したレモネードの色がわかっても、その客がリピーターになるかどうかについては、それ以上の情報は得られない。
調べてみると、男性よりも女性の方が黄色いレモネードを選ぶ傾向があることや、女性の方がリピーターになりやすいことが発見できるかもしれない。そのため、当初は黄色を選ぶと再来店しやすいように見えたが、実際には “レモネードの色 “は “性別” を介してのみ “再来店 “に関係している。だから、回帰に “Sex “を含めると、”Lemonade color “は回帰から脱落する。
ある変数が統計的に有意だからといって、それが実際に因果関係があるとは限らない。しかし、注意深く変数を足したり引いたりし、モデルがどのように変化するかを記録し、モデルの背後にある理論について常に考えることで、データから興味深い関係を切り離すことができる。
第2段階:モデルをアセスメントする。
変数を足したり引いたりするたびに、r2乗(R2)、AICc、Stats iQからのアラートを見て、モデルの精度を評価する必要があります。モデルを変更するたびに、新しいr2乗、AICc、診断プロットを古いものと比較し、モデルが改善されたかどうかを判断する。
R2乗 (R2)
モデルの予測精度を数値化する指標はr2乗と呼ばれ、0から1の間で表される。ゼロはそのモデルに予測力がないことを意味し、1はそのモデルがすべてを完全に予測していることを意味する。
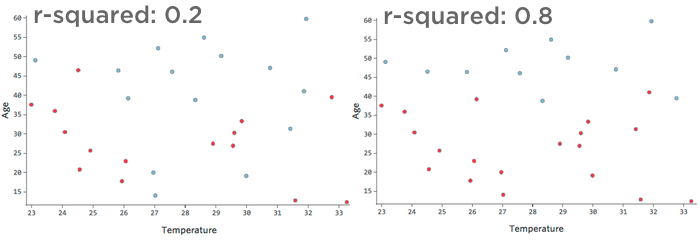
例えば、左のデータは右のデータよりもはるかに精度の低いモデリングになる。散布図に線を引こうとしているところを想像してみてほしい。右側では青(「戻った」)と赤(「戻らなかった」)をほぼ完全に分けることができるが、左側では難しいだろう。
つまり、右側のr2乗が高い。「温度」と「年齢」がわかれば、「返品」対「返品」を判断できる。”しなかった “のは簡単だ。温度」と「年齢」がわかれば、、「返品」対「返品」かをかなり正確に推測できる。”しなかった “が、エラーは多いだろう。
良い」r2乗に決まった定義はない。ある環境では、まったく効果が見られないことが面白いかもしれないし、ある環境では、モデルが高精度でない限り役に立たないかもしれない。
変数を追加すればするほどr2乗は上がるので、可能な限り高いr2乗を達成することがゴールではなく、むしろモデルの精度(r2乗)と複雑さ(一般的には変数数)のバランスを取りたいのです。
AICc
AICcは精度と複雑さのバランスをとる指標であり、精度が高いほどスコアが良くなり、複雑さ(変数が多い)が増すとスコアが悪くなる。AICcの低いモデルの方が優れている。
AICc指標は、同じ行数のデータ、同じ出力変数を持つモデルのAICcを比較する場合にのみ有用であることに注意。
アラート
Stats iQは随時、あなたのモデルを改善する方法を提案します。例えば、Stats iQは変数の対数を取ることを提案することがあります(その意味についての詳細)。
混乱マトリックスと精度-再現曲線
混同マトリックスと精度-再現曲線も、モデルの精度を理解するのに便利なツールです。そして、もしあなたが自分のモデルに基づいて予測をしたいのであれば、これらのツールがその手助けをしてくれるだろう。これらの情報は、モデルが何を語っているかをよく理解するために、厳密には必要ではないので、混同マトリックスと精度-再現曲線については
別のセクションで説明します。
第3段階:適宜モデルを修正する。
モデルのアセスメントが満足のいくものであった場合、これで終了するか、ステージ1に戻ってさらに変数を入力することができます。
アセスメントでモデルに不足が見つかれば、Stats iQのアラートを使って問題を修正する。
モデルを修正する際には、r2乗、AICR、残差診断の変化に絶えず注意し、あなたが行っている変更がモデルを助けているのか、それとも傷つけているのかを判断します。