線形回帰のユーザーフレンドリーなガイド
回帰とは何か?
回帰は、1つまたは複数の入力変数を1つの出力変数に関係付ける数式を推定する。
例えば、あなたがレモネード・スタンドを経営していて、何が収益の原動力になっているかに興味があるとしよう。あなたのデータには、各日の “売上”、最高 “気温”、”通りかかった子供の数”、”通りかかった大人の数”、その日に使用した “看板”、近隣の “競合店の売上 “が含まれます。
| 収入 | 温度 (摂氏) | 休憩時間 | 通りかかった子供の数 | 通りかかった大人の数 | 看板 | 競合他社の売上高 |
|---|---|---|---|---|---|---|
| 44ドル | 28.2 | 30 | 43 | 380 | ハンドペイント | $20 |
| 23ドル | 21.4 | 42 | 28 | 207 | LED | 30ドル |
| 43ドル | 32.9 | 14 | 43 | 364 | ハンドペイント | $34 |
| 30ドル | 24.0 | 24 | 18 | 103 | LED | $15 |
| その他 | その他 | その他 | その他 | その他 | その他 | その他 |
あなたは、”温度”(入力または説明変数)が “収益”(出力または応答変数)に影響を与えるかもしれないと考えています。回帰を使ってこの関係を分析すると、次のような式が得られるかもしれない
:Revenue = 2.71 * Temperature – 35この
式が有用な理由は2つある。
まず、暑い日が続くと “収入 “が増えるという関係を理解することができる。特に、”温度 “の前の2.71(係数と呼ばれる)は、”温度 “が1度上がるごとに、平均して2.71ドルの “収入 “が増えることを意味する。このインサイトによって、寒い日にはレモネードを売らないと決めるかもしれない。
第二に、それに関連して、ITは具体的な予測を立てるのにも役立つ。仮に “温度 “が24だとすると、…
収入=2.71 * 温度 – 35
収入=2.71 * 24 – 35
収入=30
…約30ドルの “収入 “があることになる。自分のモデルが正確であると確信しているのであれば、その日の支払いが可能かどうかを知るために有用な情報かもしれない。
では、この回帰式を作成するプロセスを説明しよう。
回帰モデルを作成する準備
1.回帰のセオリーを考えよう
回答変数「回答収入」を選んだら、様々なインプットがITとどのように関連しているか仮説を立てます。例えば、「温度」が高ければ「収益」が上がると考えたり、様々な看板が「収益」にどのような影響を与えるのか確信が持てなかったり、 「競合の売上」は「温度」の影響を受けるが、あなたのレモネード・スタンドには何の影響もないと考えたりするかもしれません。
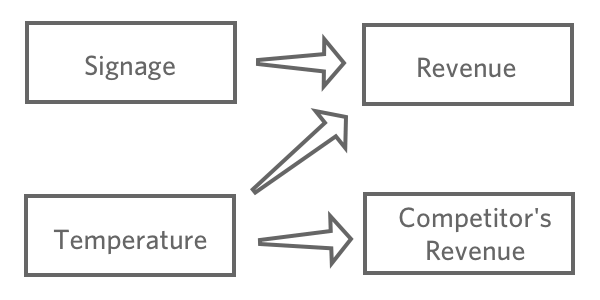
回帰の目的は、通常、いくつかの入力と1つの出力の関係を理解することです。したがって、この場合、おそらく「温度」、「看板」 (実際の予測よりも説明に興味があるとしても、 「温度と看板から収益を予測する」とも言います)を使って「収益」を説明するモデルを作成することになるでしょう。
競合他社の売上」を回帰に含めることはおそらくないだろう。それは「収入」と相関している可能性が高いが、因果関係の連鎖の中では「収入」の前に来ていないので、それを含めるとモデルが混乱してしまう。
2.モデルに役立つ可能性のあるすべての変数を「記述」する。
回答変数(この場合は「回答収益」)を説明し、その感触をつかむことから始めます。説明変数についても同様にしてください。
…ほとんどのデータがヒストグラムの最初の数ビンにある。これらの変数には、後で特別な注意を払う必要がある。
3.可能性のあるすべての説明変数を応答変数に “関連付ける”
Stats iQは、結果を統計的関係の強さ順に並べます。どの変数がどのように「収益」と関連しているかに注目しながら、見た目と操作性を確かめてください。
もし、理論的にどの変数が出力を駆動するべきか(例えば、過去の学術論文から)、すでに良いアイデアを持っているなら、このステップは飛ばすべきである。しかし、あなたの分析がもう少し探索型である場合(顧客アンケートのような)、これは有用で重要なステップです。
4.リグレッションの構築開始
回帰モデルの構築は反復プロセスである。以下の3段階を必要なだけ繰り返す。
回帰モデル構築の3つの段階
ステージ 1: 変数の加算または減算
一つずつ、以前の分析で「収益」に関連していると示された変数を追加し始める(または、追加する理論的理由がある変数を追加する)。1つ1つ確認することは厳密には必要ではないが、確認しながら問題を修正することが容易になり、モデルの感覚をつかむのに役立つ。
例えば、”収益 “を “気温 “で予測することから始めるとしよう。強力な関係を見つけ、モデルをアセスメントし、満足のいくものであると判断する(詳細は後ほど)。
収益=2.71 * 温度 – 35
次に、「通りかかった子供の数」を加えると、回帰モデルには2つの項ができ、どちらも統計的に有意な予測因子となる。
次に
、「通りかかった大人の数」を追加すると、モデル結果は、「大人の数」はモデル内で統計的に有意であるが、「子供の数」はもはや有意ではないことを示す。通常、モデルから「子供の数」を削除する。今、私たちにはそれがある:
収益 = 2.6 * 気温 + 0.4 * 大人の歩行者数 – 14
つまり、大人が何人来たかを知っていれば、子供が何人来たかを知っても新たな情報は追加されず、売上予測には役立たない。
思い返してみれば、子どもたちがあなたのレモネードを買ってくれることはないのだから、その変数がモデルに帰属意識を持っていないのは理にかなっている。
最初のモデルで統計的に有意だったのはなぜか?おそらく、”子供の数 “は “大人の数” と相関があり、”大人の数 “がまだモデルに入っていなかったため、”子供の数”が “大人の数 “の大まかな代理として機能していたのだろう。
ある変数が統計的に有意だからといって、それが実際に因果関係があるとは限らない。しかし、注意深く変数を足したり引いたりし、モデルがどのように変化するかを記録し、モデルの背後にある理論について常に考えることで、データから興味深い関係を切り離すことができる。
ステージ2:モデルのアセスメント
変数を追加または減算するたびに,r2 乗(R2),AICR,残差プロットを見ることによって,モデルの正確さを評価するべきである.モデルを変更するたびに、新しいr2乗、AICR、残差プロットを古いものと比較し、モデルが改善されたかどうかを判断します。
R2乗 (R2)
モデルの予測精度を数値化する指標はr2乗と呼ばれ、0から1の間で表される。ゼロはモデルに予測力がないことを意味し、1はモデルがすべてを完全に予測することを意味する。
例えば、左のモデルは右のモデルよりも正確である。つまり、「Temperature」がわかっていれば、左の「Revenue」。
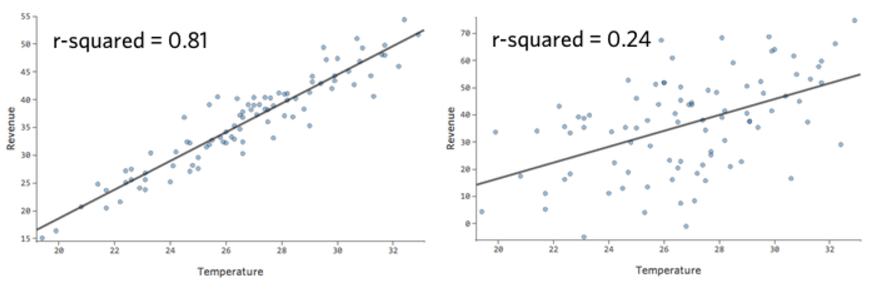
良い」r2乗に決まった定義はない。ある環境では、まったく効果が見られないことが面白いかもしれないし、ある環境では、モデルが高精度でない限り役に立たないかもしれない。
変数を追加すればするほどr2乗は上がるので、可能な限り高いr2乗を達成することがゴールではなく、むしろモデルの精度(r2乗)と複雑さ(一般的には変数数)のバランスを取りたいのです。
AICR
AICRは、精度と複雑さのバランスをとる指標であり、精度が高いほどスコアが良くなり、複雑さ(変数が多い)が増すとスコアが悪くなる。AICRの低いモデルの方が優れている。
AICR指標は、同じ行数のデータ、同じ出力変数を持つモデルのAICRを比較する場合にのみ有用であることに注意。
予測間隔
モデルの精度を知るもう一つの便利な方法は、サンプル値を計算式に入れ、Stats iQが算出する予測区間を見ることです。例えば、30という数字を数式に突っ込むと、予測値は45.5だが、95%信頼区間は36.4から54.5であり、明日が30度になった場合、”収入 “は36.40ドルから54.50ドルの間であると95%の確率で言えるとSTATS iQは教えてくれる。予測間隔が44ドルから48ドルのような狭い範囲であればより正確なモデルが、20ドルから72ドルのような広い範囲であればあまり正確でないモデルが想像できるだろう。
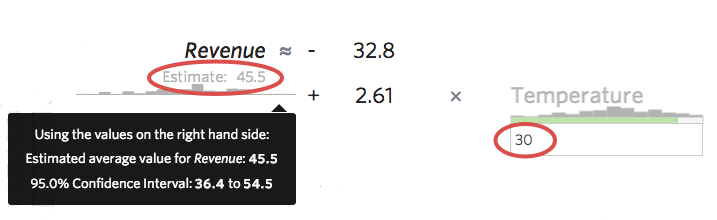
この方法は、残差プロットが健全に見える場合にのみ有効で(下記参照)、そうでない場合は不正確になる。
残差
残差は、回帰をアセスメントして改善するための主要な診断ツールです。したがって、モデルを改善するための残差の解釈については、まったく別のセクションがあります。残差とは何か、モデルをアセスメントし改善するために残差をどのように使うか、モデルをどの程度正確にする必要があるかについてどのように考えるかについて、学んだり記憶を新たにしたりすることができます。
素晴らしいモデルを作るために必要な他のすべてを網羅しているので、全文を読むことをお勧めする。しかし、もちろん、いつでも戻ってくることができる。
ステージ3:モデルを適宜修正する
モデルのアセスメントが満足のいくものであれば、これで終了です。または、ステージ1に戻って、さらに変数を入力することもできます。
アセスメントでモデルに不足が見つかれば、Stats iQのアラートと残留診断セクションを使って問題を修正する。
モデルを修正する際には、r2乗、AICR、残差診断の変化に絶えず注意し、あなたが行っている変更がモデルを助けているのか、それとも傷つけているのかを判断します。