回帰を改善するための残存プロットの解釈
回帰を実行すると、Stats iQは自動的に残差を計算してプロットし、回帰モデルの理解と改善に役立てます。残差の解釈について知っておくべきこと(定義や例を含む) については、以下を参照してください。
観察、予測、残差
残差の解釈方法を示すために、各行が1日の「温度」と「収益」であるレモネードスタンドデータセットを使用します。
| 温度 (摂氏) | 収益 |
|---|---|
| 28.2 | 44ドル |
| 21.4 | 23ドル |
| 32.9 | 43ドル |
| 24.0 | 30ドル |
| その他 | その他 |
「気温」と「収益」の関係を説明する回帰方程式は次のとおりです。
収益 = 2.7 * 気温 – 35
ある日のレモネードスタンドの気温が30.7度、「収益」が50ドルだったとしましょう。50は観察された出力、つまり実際の出力(実際に発生した値) です。
したがって「気温」の値に30.7を挿入すると…
収益 = 2.7 * 30.7 – 35
収益 = 48
…48 ドルになります。これは、その日の予測値です。回帰方程式が「気温」に基づいて予測した「収益」の値とも呼ばれます。
もちろん、モデルが必ずしも完ぺきであるとは限りません。この場合、予測は2だけ外れ、その差異2が残差と呼ばれます。残差は、観察値から予測値を差し引いて残った部分です。
残差 = 観察値 – 予測値
すべてのデータ行に予測と残差を追加するとこのようになります。
| 気温 (摂氏) |
収益 (観察値) |
収益 (予測値) |
残差 (観察値 – 予測値) |
|---|---|---|---|
| 28.2 | 44ドル | 41ドル | 3ドル |
| 21.4 | 23ドル | 23ドル | 0ドル |
| 32.9 | 43ドル | 54ドル | -11ドル |
| 24.0 | 30ドル | 29ドル | 1ドル |
| その他 | その他 | その他 | その他 |
観察、予測、残差の値を使用して、モデルを評価および改善します。
観察値と予測の正確性の理解
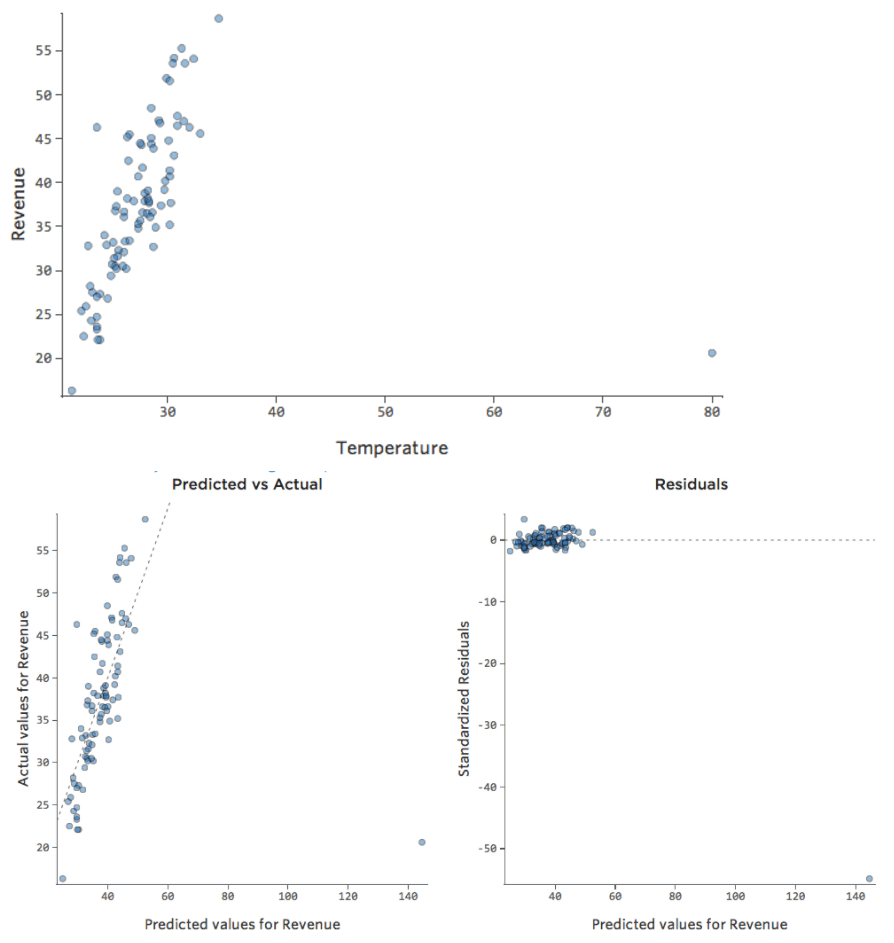
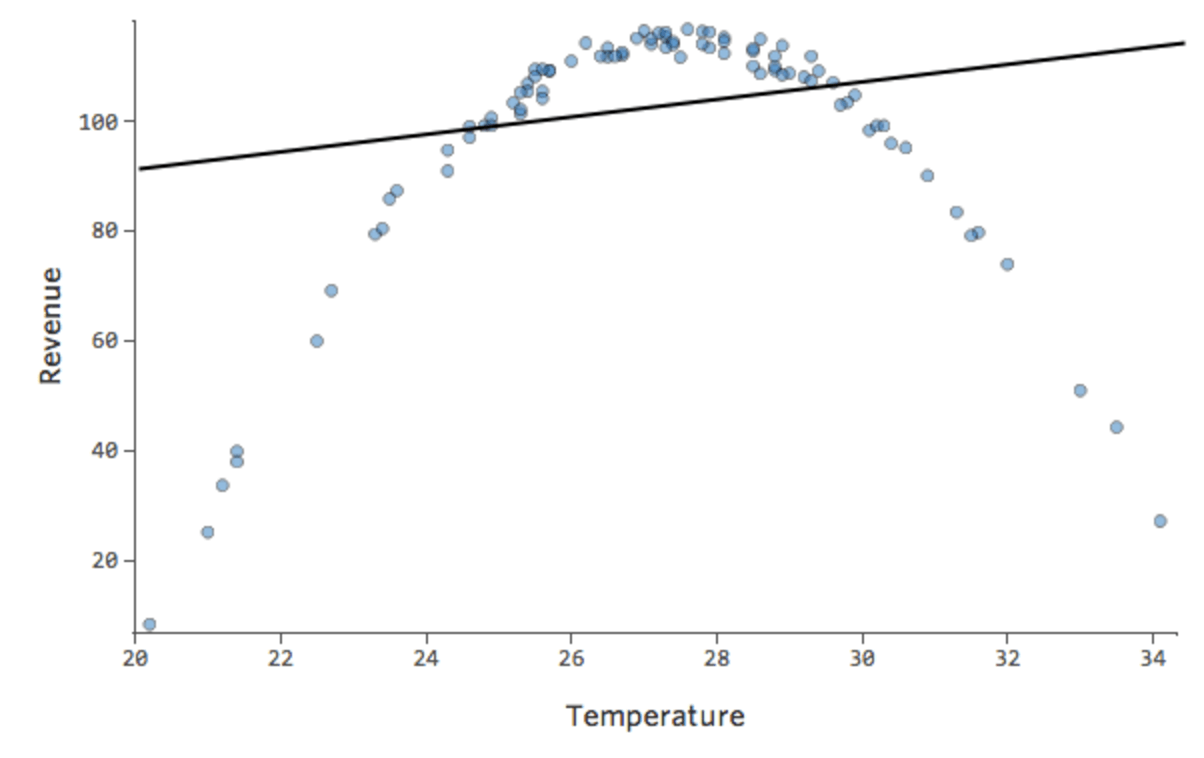
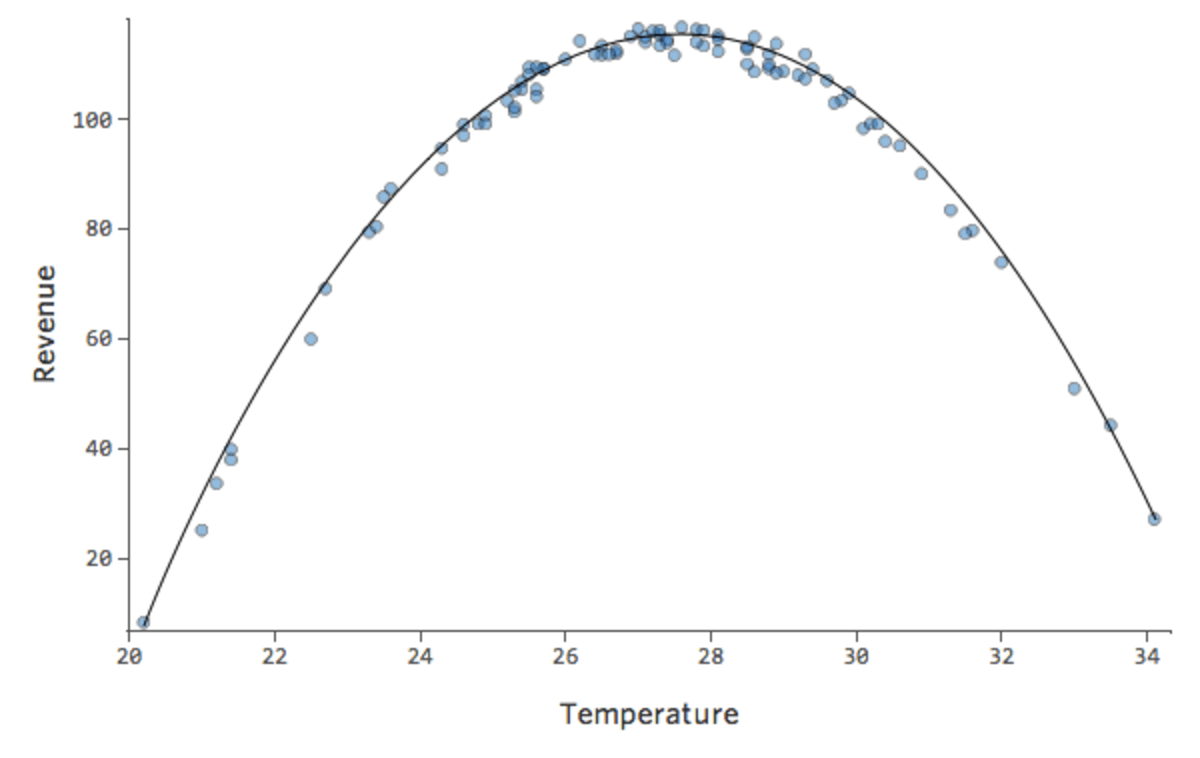
このような単純なモデルでは、2つの変数のみを使用して、「温度」と「収益」を関連付けるだけで、モデルの精度を把握することができます。2つの異なるレモネードスタンドで同じ回帰が実行されます。1つはモデルが非常に正確で、もう1つはモデルが正確でない場合です。
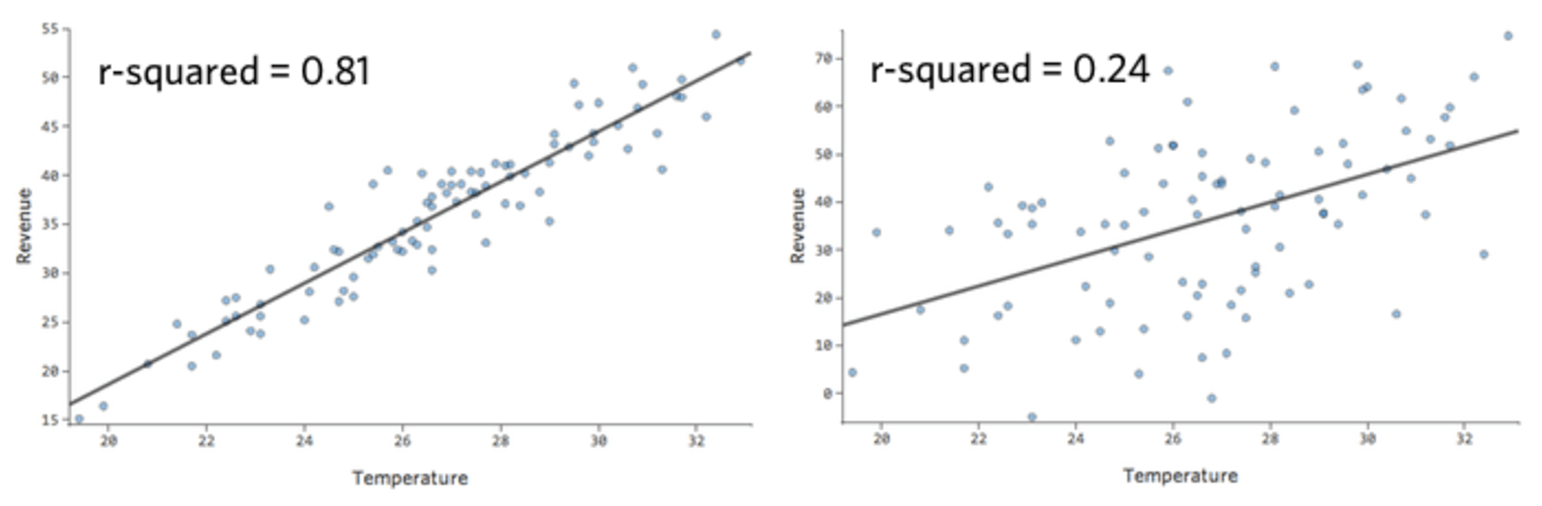
どちらのレモネードスタンドについても、「温度」の高さと「収益」の高さが関連付けられることは明らかです。しかし、所定の「温度」では、左のレモネードスタンドの「収入」の方が右のレモネードスタンドよりもはるかに正確に予測していることから、モデルがより正確であることがわかります。
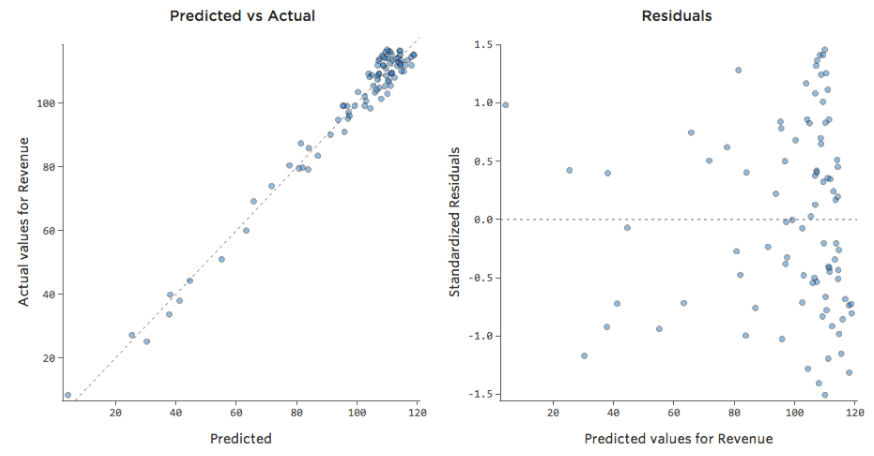
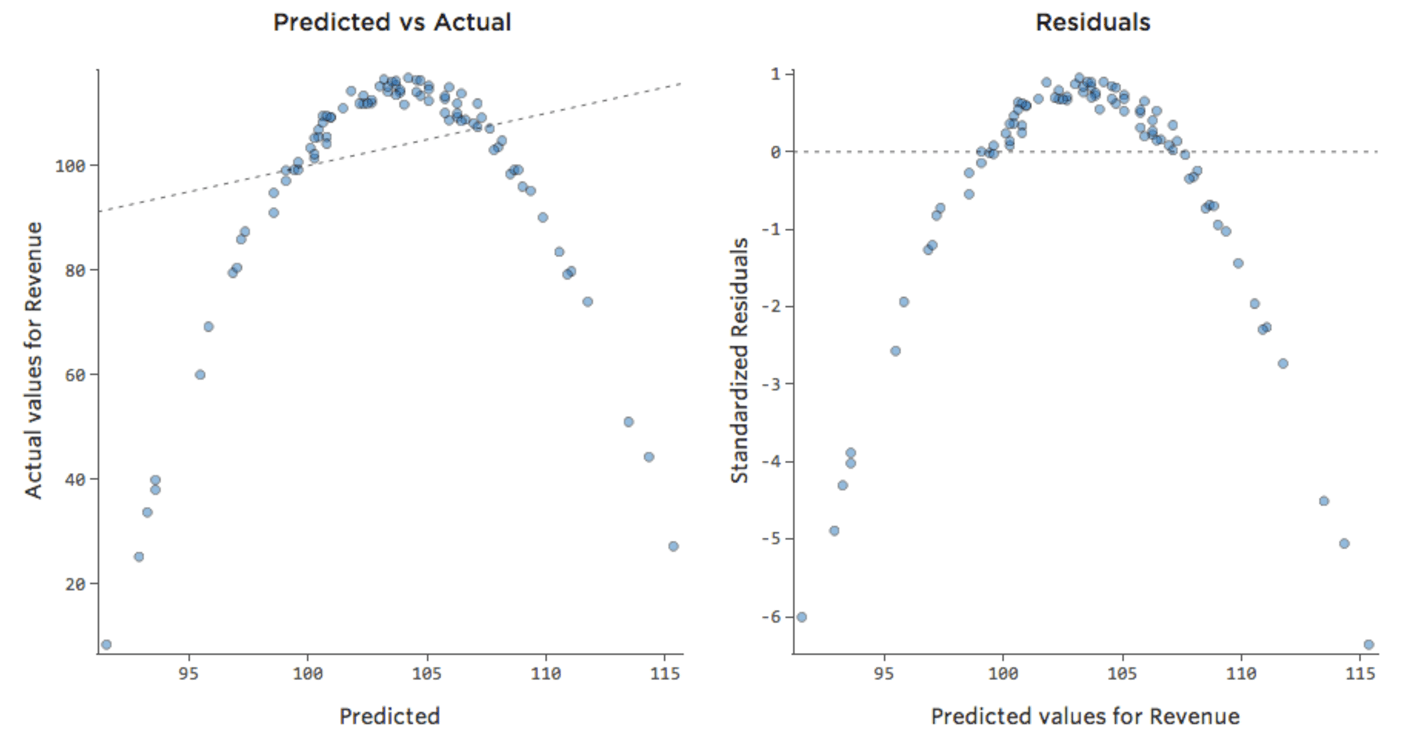
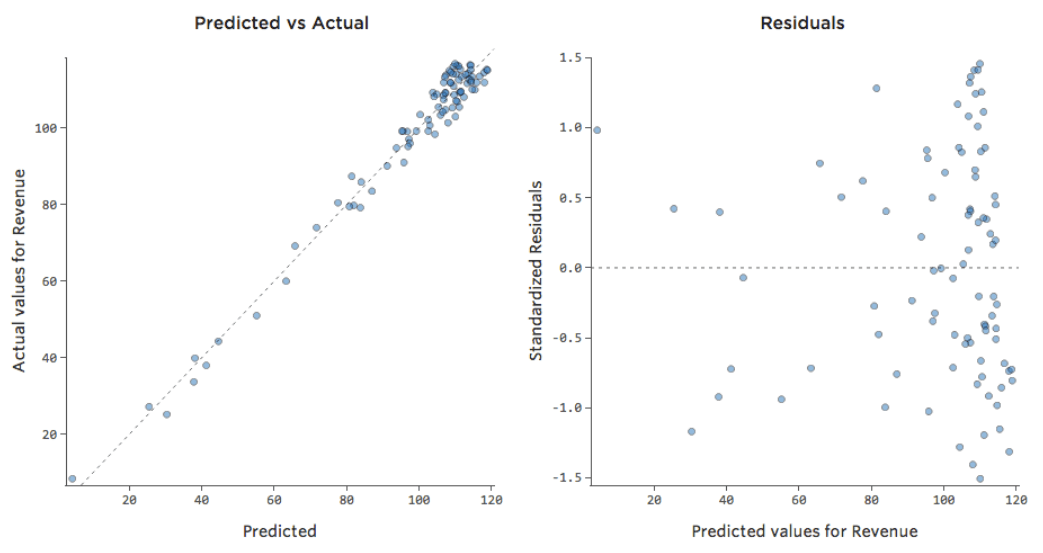
ただし、ほとんどのモデルには複数の説明変数があり、そのようなチャートでより多くの変数を表すのは実用的ではありません。そこで、これらの同じデータセットの予測と観察値をプロットしてみましょう。
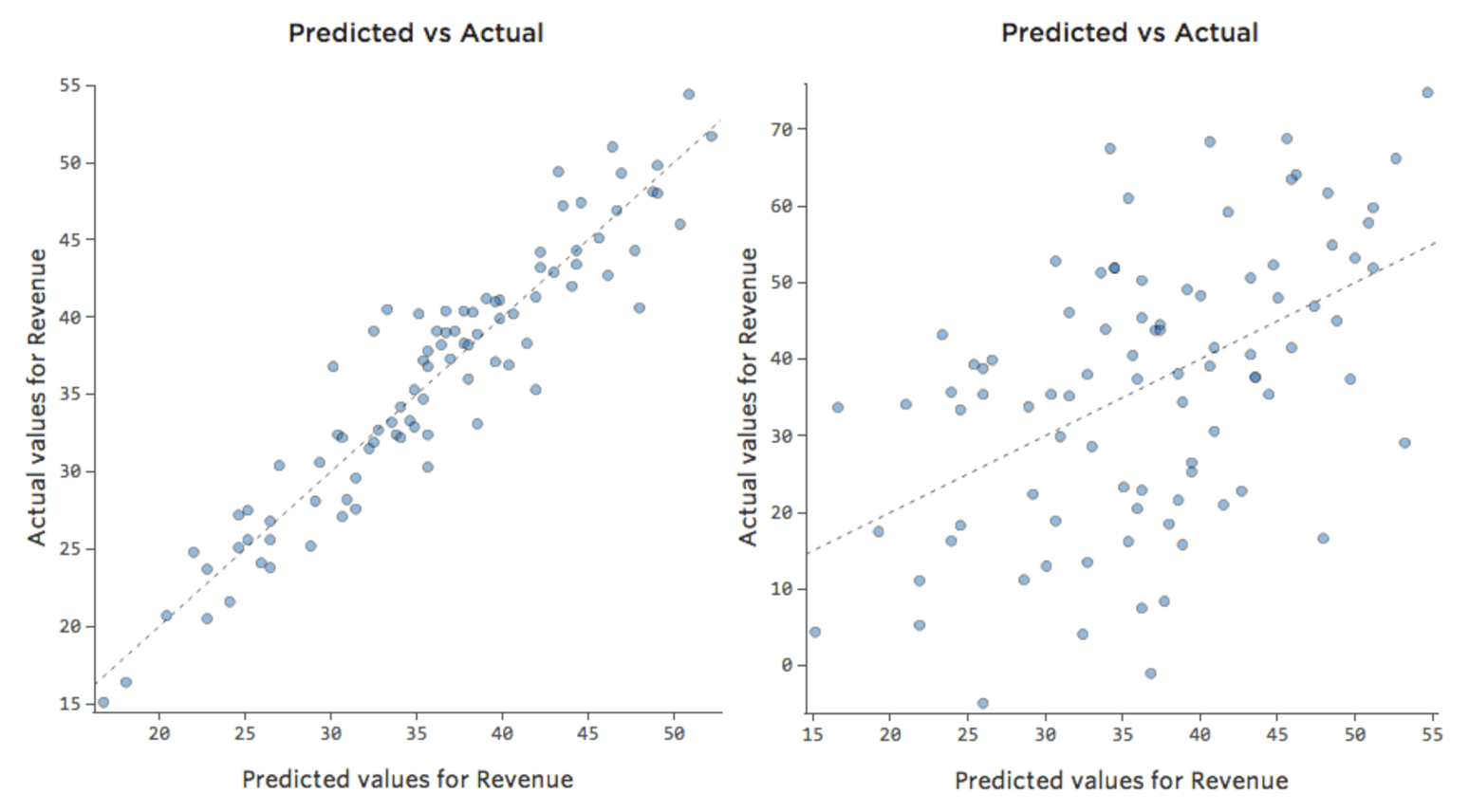
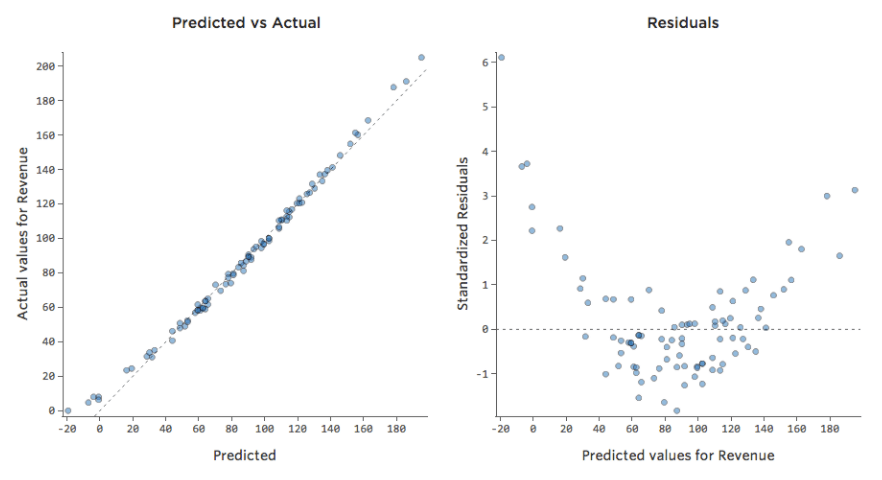
ここでも、左側のチャートのモデルは非常に正確です。モデルの予測と実際の結果との間に強い相関関係があります。右端にあるチャートのモデルでは、モデルの予測はあまり良好ではありません。
これらのチャートは、上にある「気温」対「収益」 のチャートとまったく同じに見えます。しかしX軸は「温度」ではなく予測された「収益」であることに注意してください。このようなことは、回帰方程式に説明変数が1つしかない場合には一般的です。しかし通常は、複数の説明変数を使用するケースの方が多く、そうしたチャートは「収益」に対する1つの説明変数のプロットとは大きく異なります。
予測と残差の比較(「残差プロット」)
残差をプロットする最も有用な方法は、x軸に予測値、y軸に残差を置く方法です。
(Stats iQは残差を標準化された残差として表示するため、任意のモデルで表示するすべての残差プロットは、同じ標準化Y軸上にあることになります)。
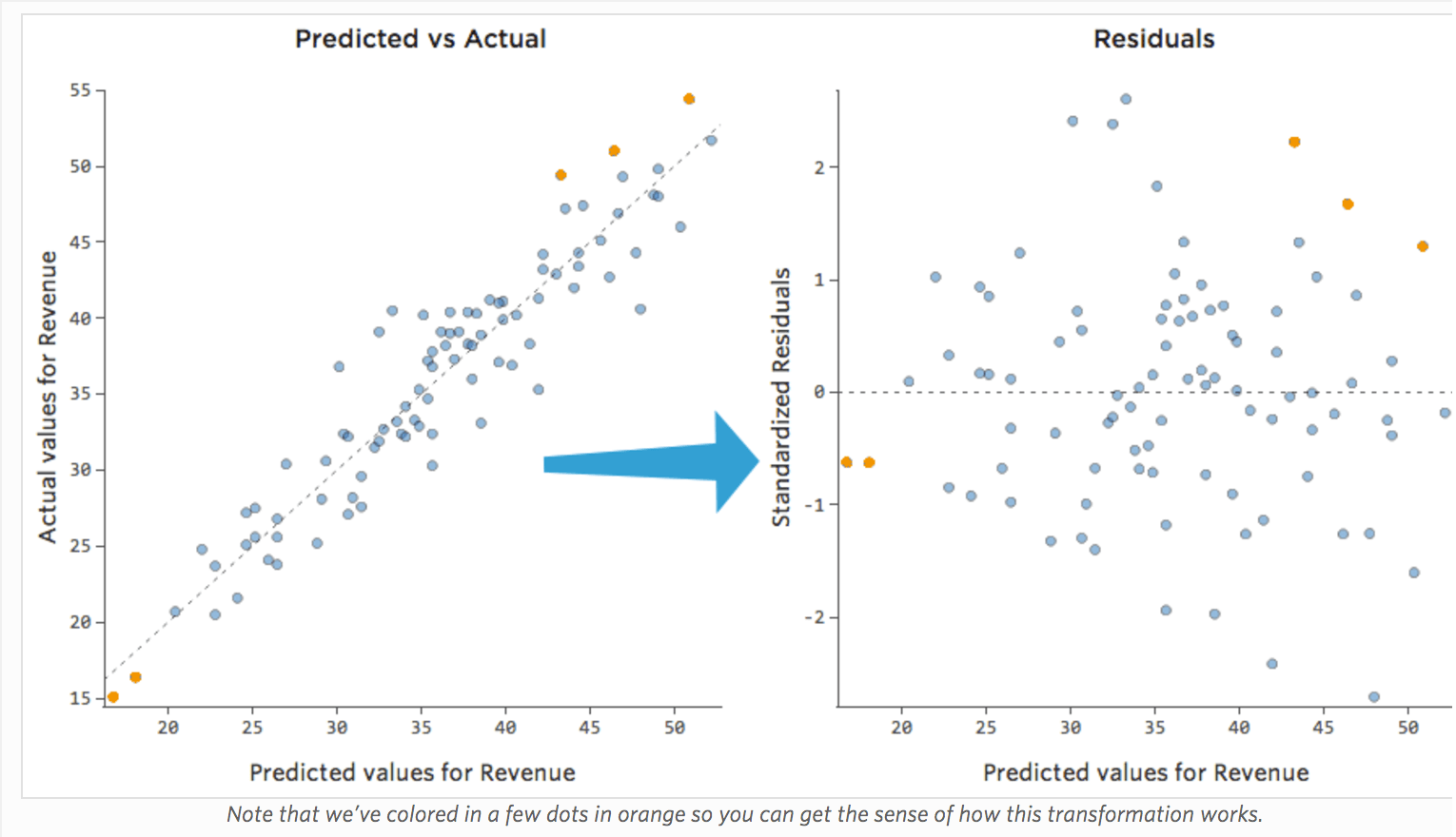
右側のプロットでは、各ポイントは1日です。ここで、モデルによる予測はx軸に、予測の精度はy軸上にあります。0のラインからの距離は、その値に対する予測精度の低さを表します。
なぜなら…
残差 = 観察値 – 予測値
…残差(Y軸上)のプラス値は予測値が低すぎることを意味し、マイナスの値は予測値が高すぎたことを意味します。0は推測が正確であったことを意味します。
つまり、
(1) 分布がかなり対称的で、プロットの中央に向かって集まる。
(2) Y軸の1桁台前半の数値(例:30や150ではなく0.5や1.5)の周辺に集まる。
(3) 一般的に明確なパターンがない。
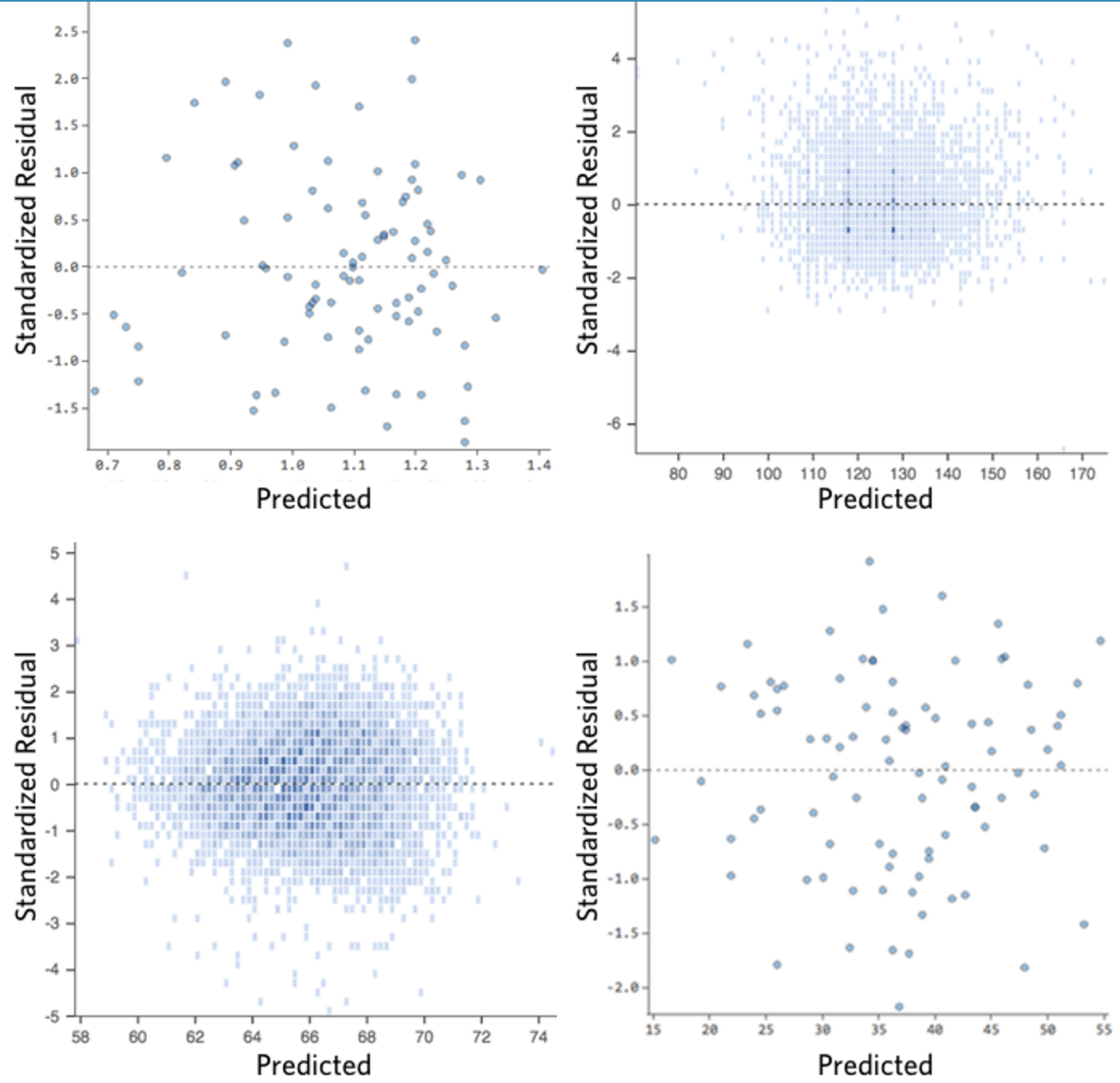
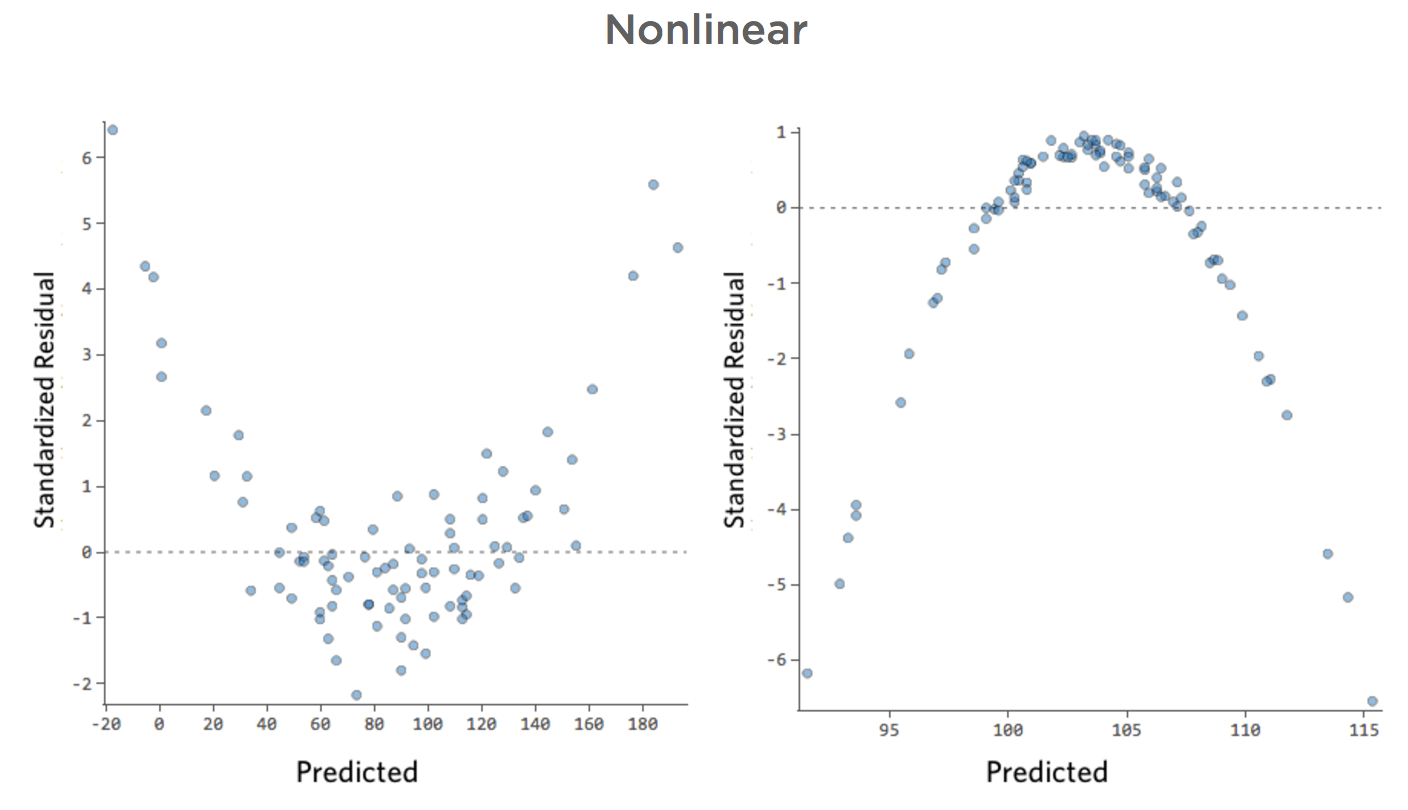
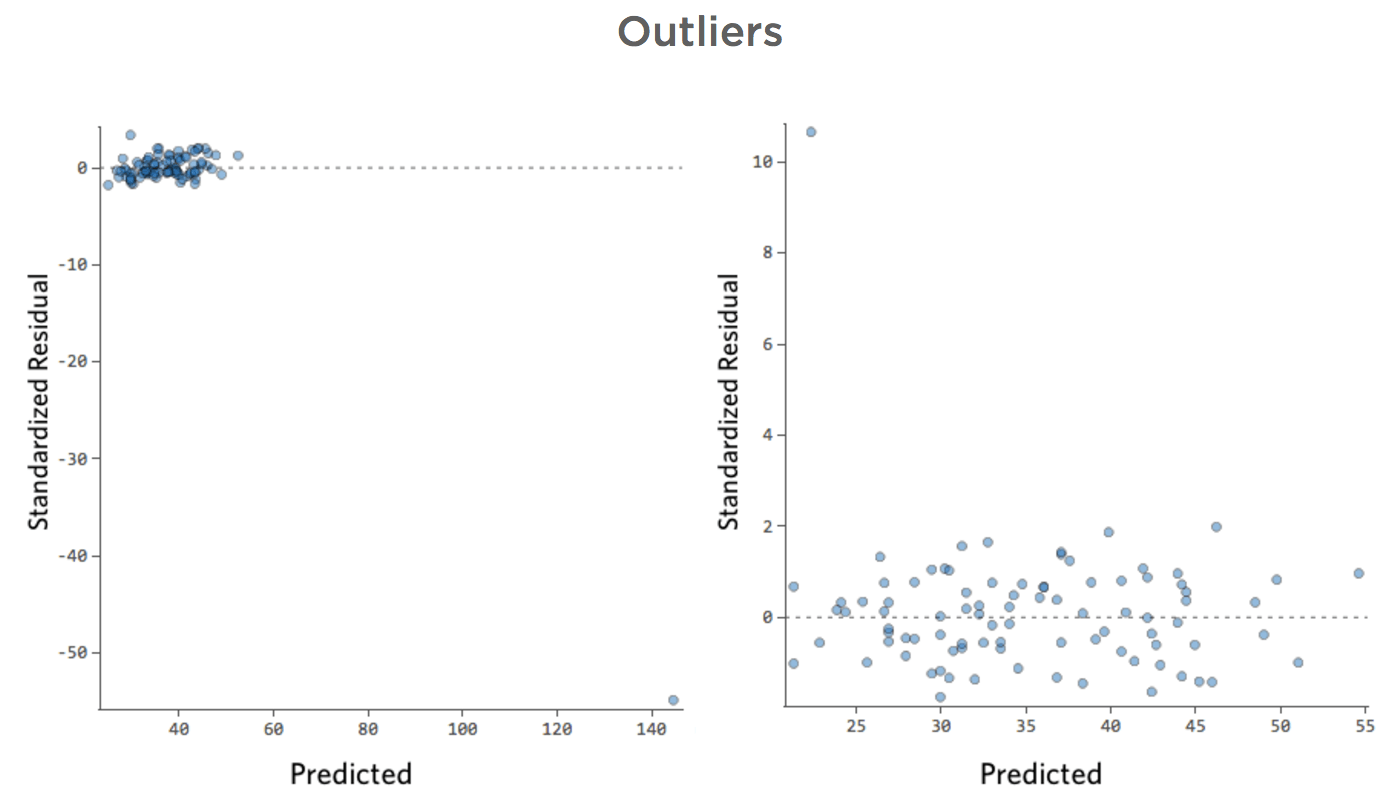
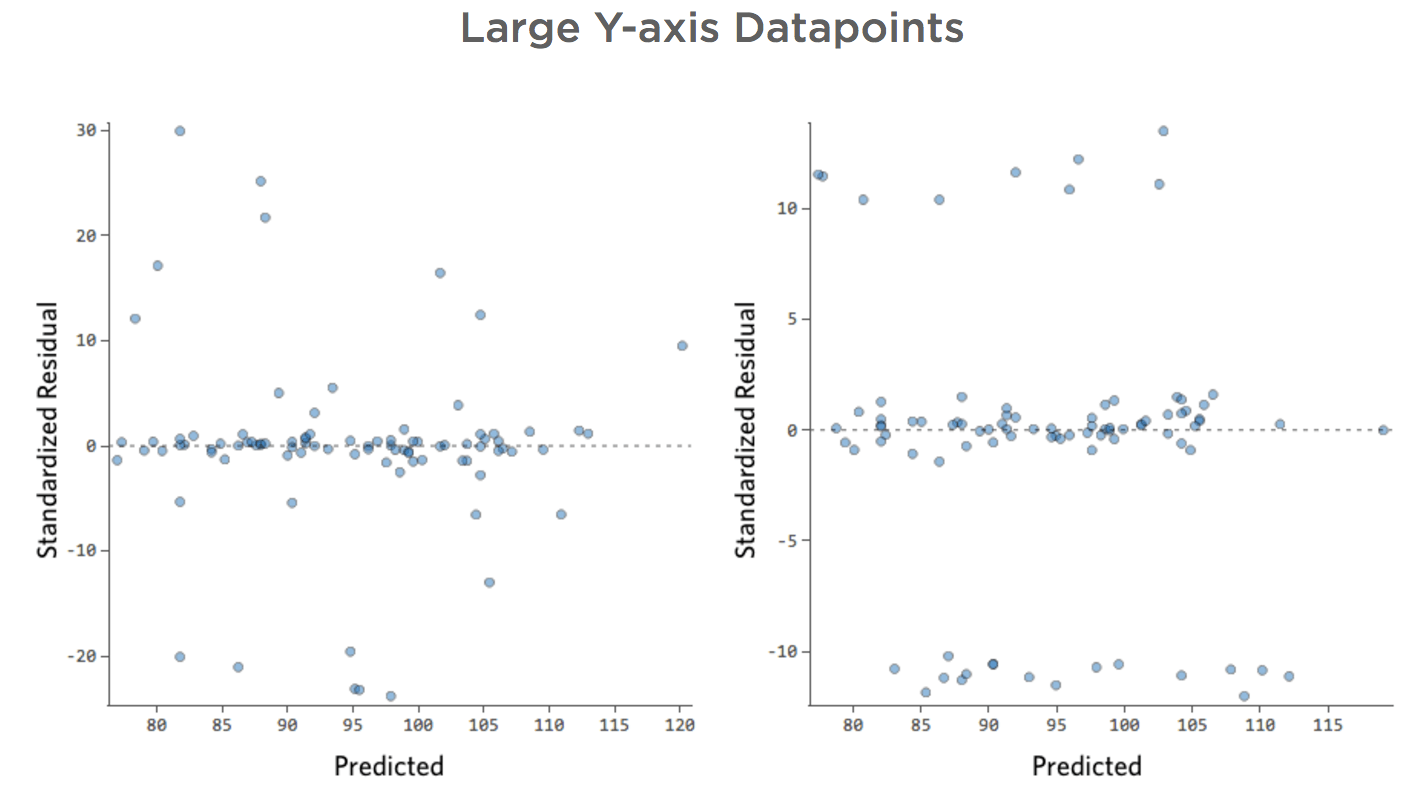
下に、これらの要件を満たさない残差プロットをいくつか示します。
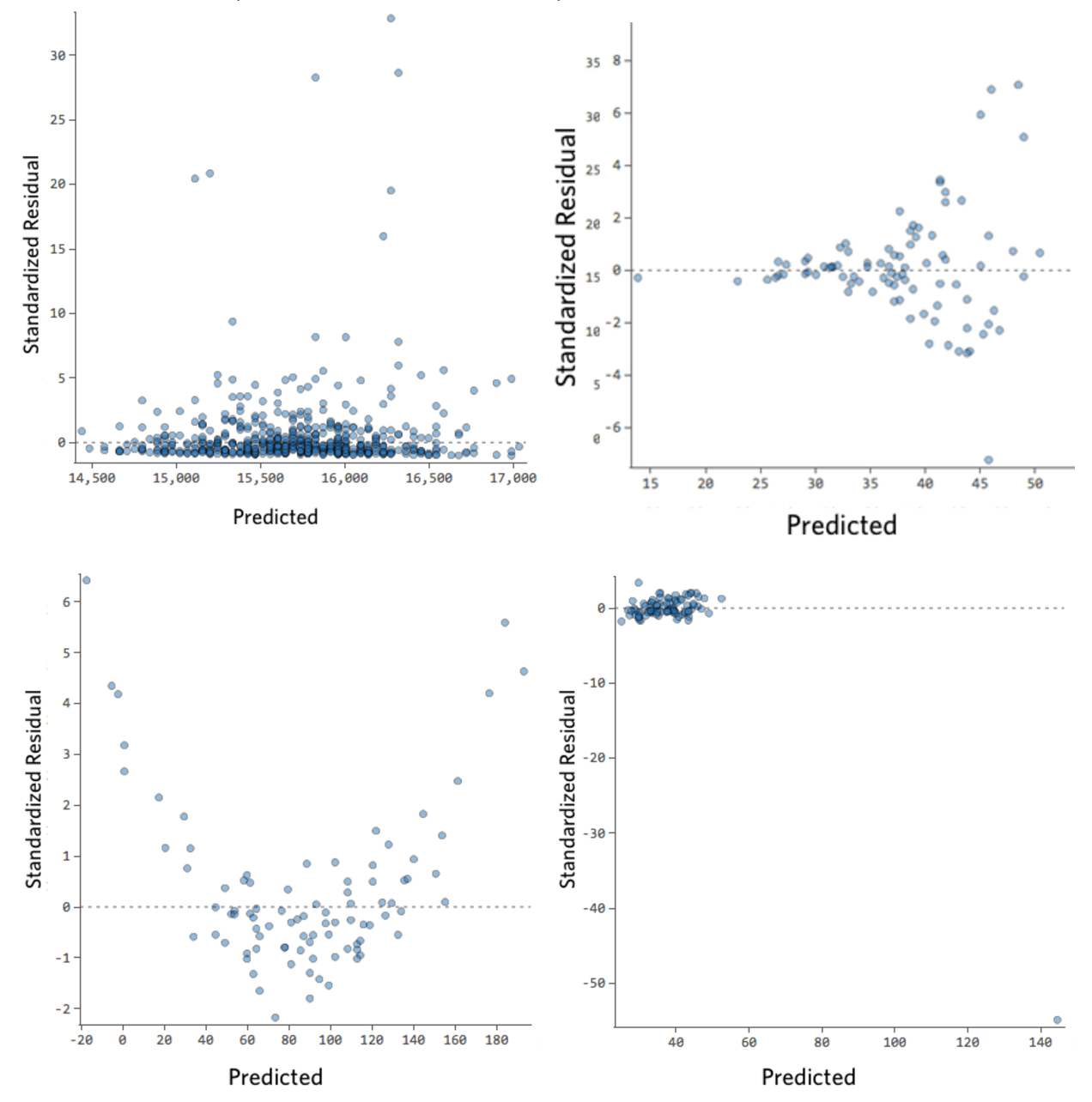
これらのプロットは、垂直方向に均等に分布していないか、外れ値があるか、明確なパターンがあります。
残差で明確なパターンまたは傾向が検出される場合は、モデルに改善の余地があります。
次に、その理由と対処方法を説明します。
正規Q-Qプロット:
[正規Q-Qプロットを表示]をクリックして、データスキューとモデル適合を評価する Q-Qプロットを表示します。このチャートでは標準化された残差がy軸に、理論的分位がx軸に表示されます。
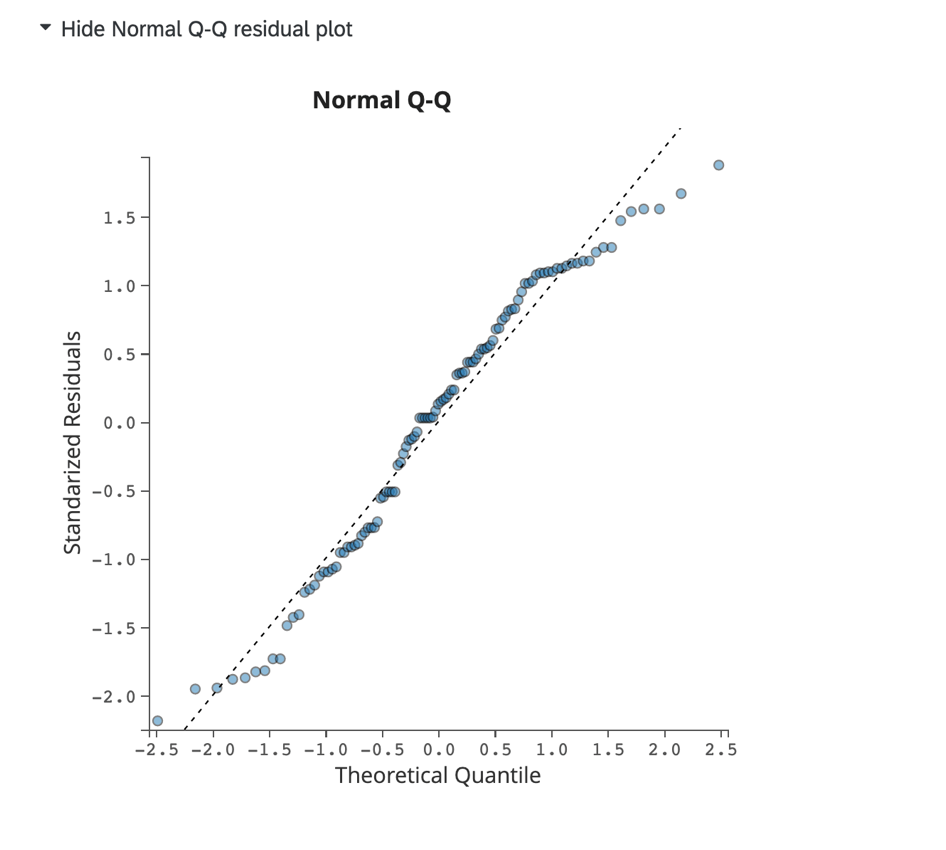 点線に近い位置に配置されるデータは正規分布を示します。点数が線から大幅に偏っている場合は、回帰モデル内の他の変数を追加または削除することで、モデルを調整することを検討できます。
点線に近い位置に配置されるデータは正規分布を示します。点数が線から大幅に偏っている場合は、回帰モデル内の他の変数を追加または削除することで、モデルを調整することを検討できます。
モデルが完ぺきでない場合の問題
モデルが不完全な場合や残差が少し不健全に見える場合、どの程度の懸念を抱くべきでしょうか。これは使用者次第です。
素粒子物理学で論文を公表している場合は、モデルが可能な限り正確であることを確認する必要があります。甥のレモネードスタンドについてすばやく大まかな分析を実行する場合、モデルがたとえ完ぺきでなくても、たいていの場合、疑問への答えを導くのに問題はないでしょう(「温度」が「収益」に影響を与えるかどうかなど)。
通常は、そこそこのモデルでも、何もないよりはよいものです。そのため、モデルを選択し、改善を試みてから、精度が目的に適しているかどうかを判断します。
残差プロットとその診断の例
残差についてよくわからない場合は、上の説明を読んでからこちらに戻ってくることをおすすめします。
以下は不健全な残差プロットの例です。残差は、以下のうち特定の1つのタイプに見えることもあれば、いくつかの組み合わせであることもあります。
以下のいずれかに似ていると思われる場合は、その残差をクリックしてその理由を理解し、修正方法を学びます。
(レモネードスタンドの「収益」とその日の「温度」をデータセット例として使用します)。
Y軸が不均衡
- このプロットの詳細と修正方法を表示します。
-
問題
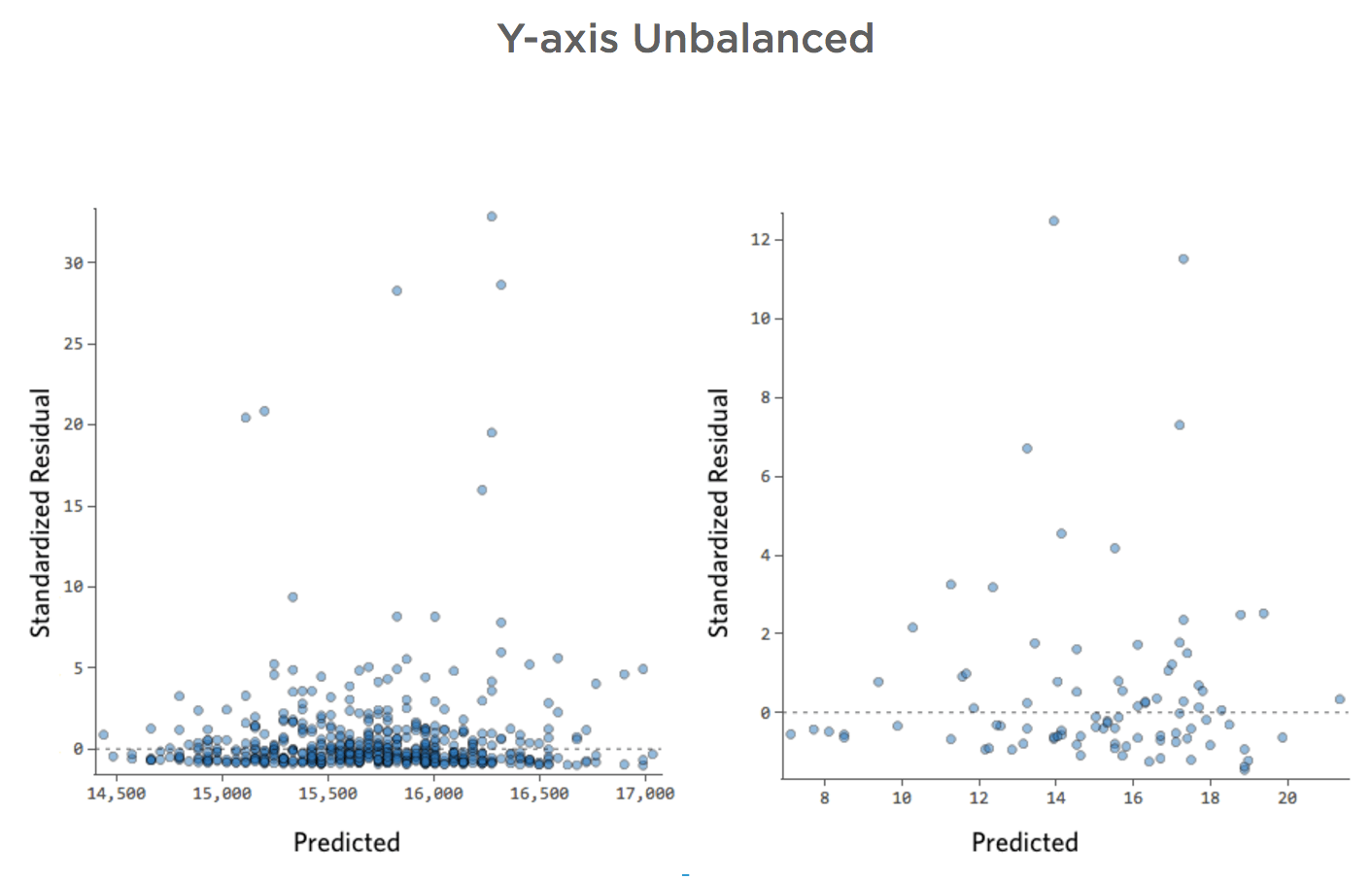
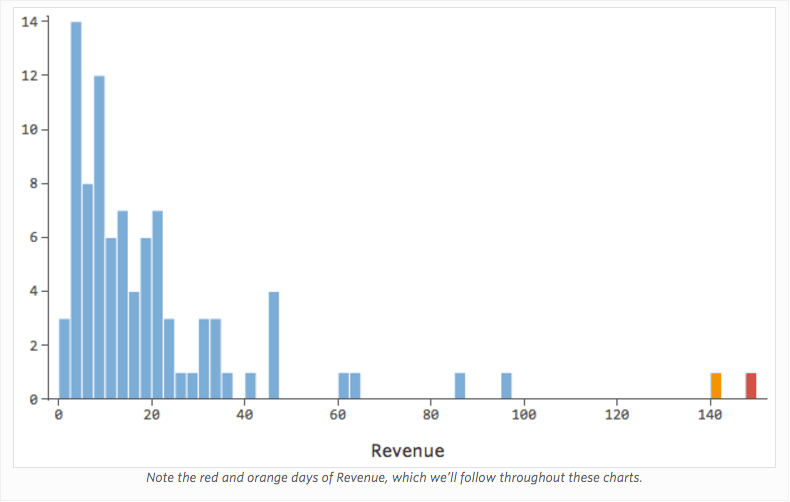
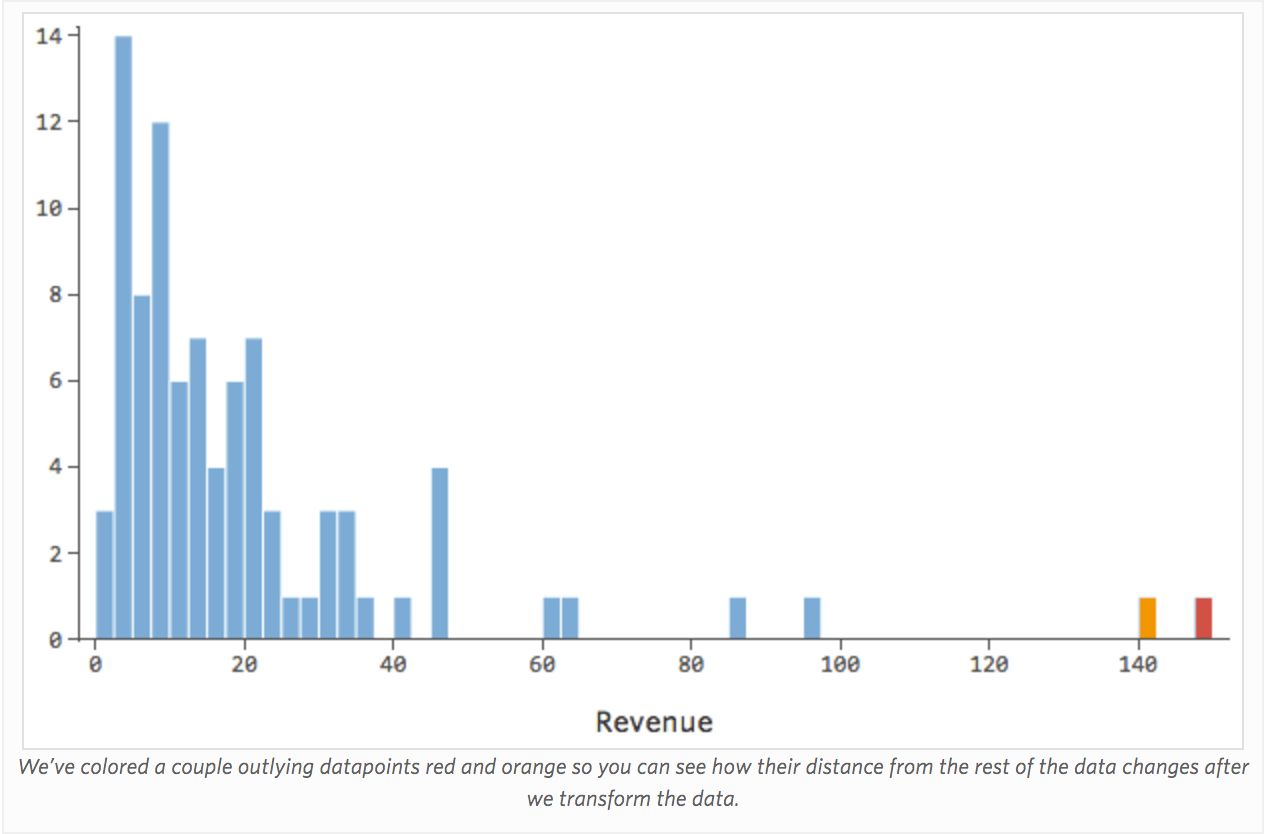
理由はどうあれ、レモネードスタンドの収益は通常は低く、何日かに一度、非常に収益の高い日があるとします。「収益」はこう見えます。
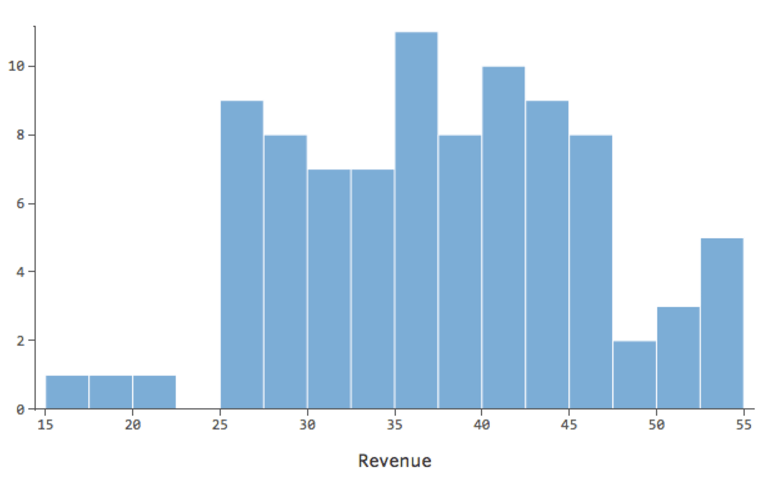
…本来は以下のようにより対称的でベル型になります。
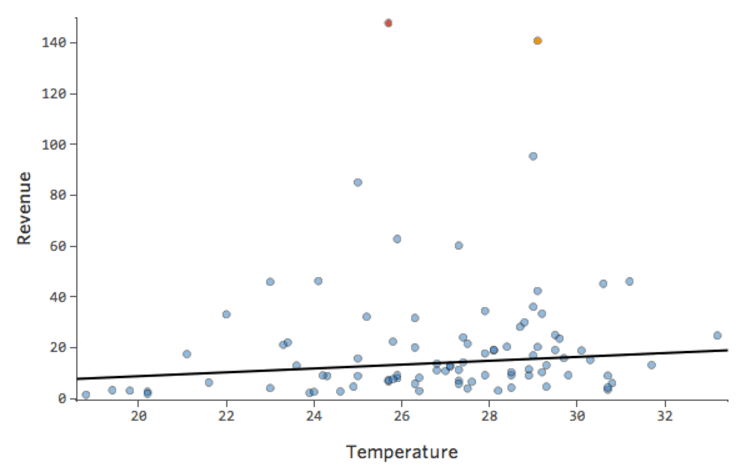
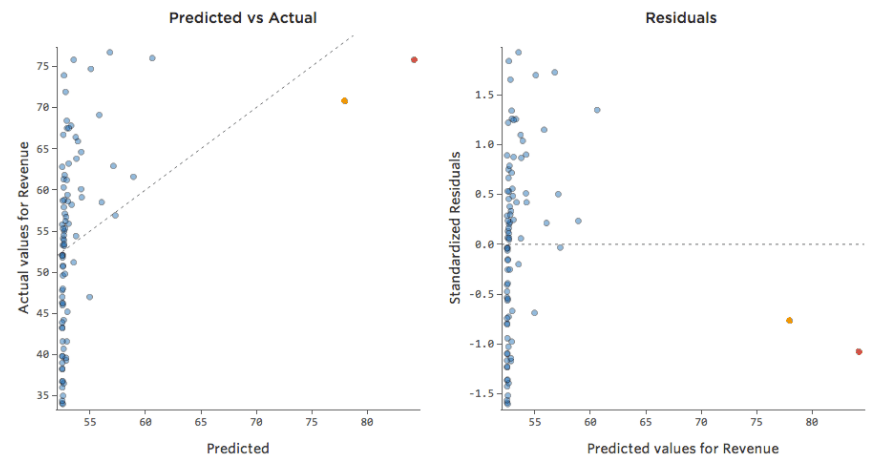
「温度」対「収益」は大部分のデータが下部に配置され、このような外観になります。
黒い線は、モデル方程式、つまり「温度」と「収益」の関係に関するモデルの予測を表します。所定の「温度」について黒線で示された各予測(たとえば「温度」30では「収入」を約20と予測)の上を見てください。大部分のドットが線の下にある(予測が高すぎた)ことがわかりますが、いくつかのドットがラインを大きく上回っています(予測がはるかに低すぎた)。
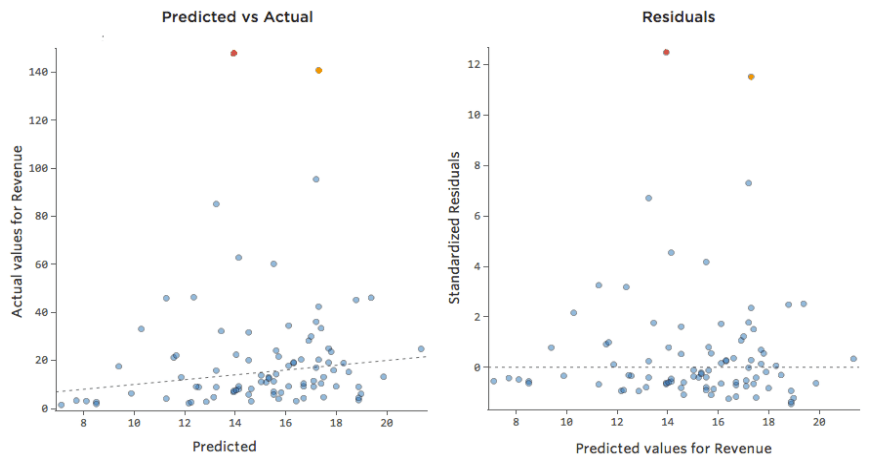
同じデータを診断プロットに変換すると、方程式の予測のほとんどが高すぎ、一部は低すぎます。
影響
これはほとんどの場合、モデルの精度に大幅に改善の余地があることを意味します。ほとんどの場合、モデルは方向性としては正しいものの、改善後のバージョンと比較するとかなり不正確であることがわかります。このような問題を修正した結果、モデルの R二乗が0.2から0.5(0から1のスケール) に跳ね上がることは珍しくありません。
修正方法
- この解決策はほとんどの場合、データを変換することです (通常は応答変数)。
- モデルに変数が欠落している可能性もあります。
不等分散性
- このプロットの詳細と修正方法を表示します。
-
問題
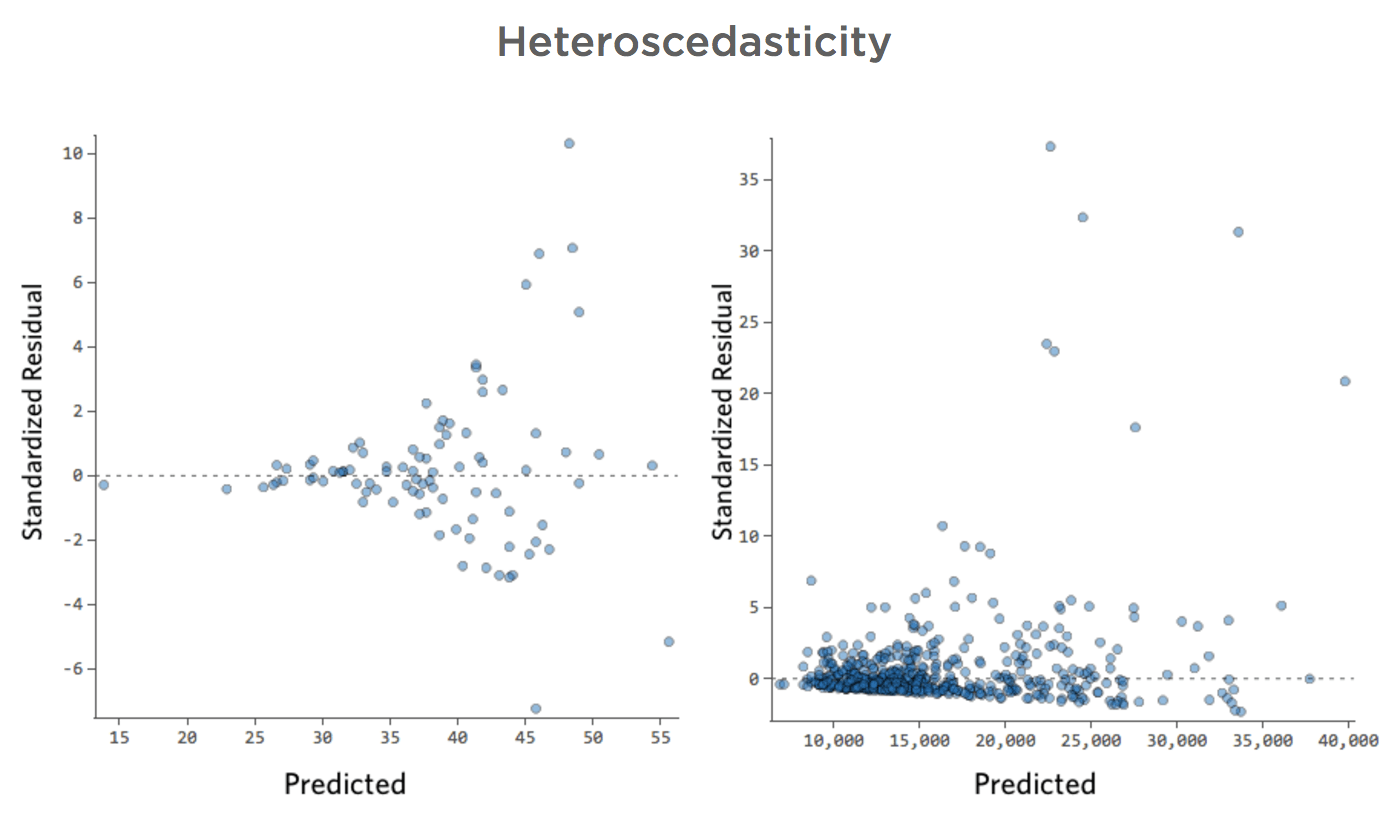
これらのプロットは、「不等分散性」を示します。予測が小さいものから大きいもの(または大きいものから小さいもの)に移行するにつれて、残差が大きくなります。
寒い日には、収益額に非常に一貫性があるものの、暑い日には収益が非常に高く、非常に少ない場合もあると仮定します。
プロットは以下のようになります。
影響
これによって本質的に問題が生じることはありませんが、多くの場合、モデルに改善の余地があることを示す指標となります。
ここでの唯一の例外は、サンプルサイズが250未満で、以下を使用して問題を修正できない場合に、P値が本来よりも少し高い、または低い場合があることです。そのため、有意境界線上にある変数が、その枠線の誤った側に誤って表示される可能性があります。ただし、回帰係数(「温度」が1つ増えると「売上高」が変化する)は引き続き正確です。
修正方法
- 通常、最も成功する解決策は変数の変換です。
- 多くの場合、不等分散性は変数が不足していることを示します。
非線形
- このプロットの詳細と修正方法を表示します。
-
問題
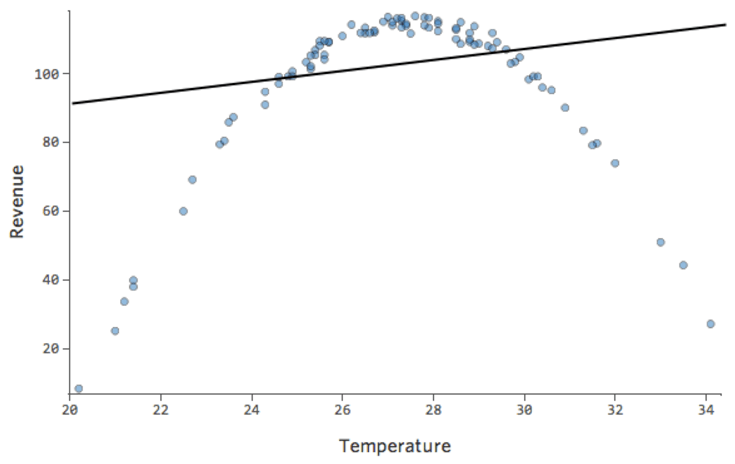
寒い日にはレモネードを売りにくく、暖かい日には売りやすく、非常に暑い日には売りにくいとします(非常に暑い日には外出する人が減るため)。
このプロットは、以下のようになります。
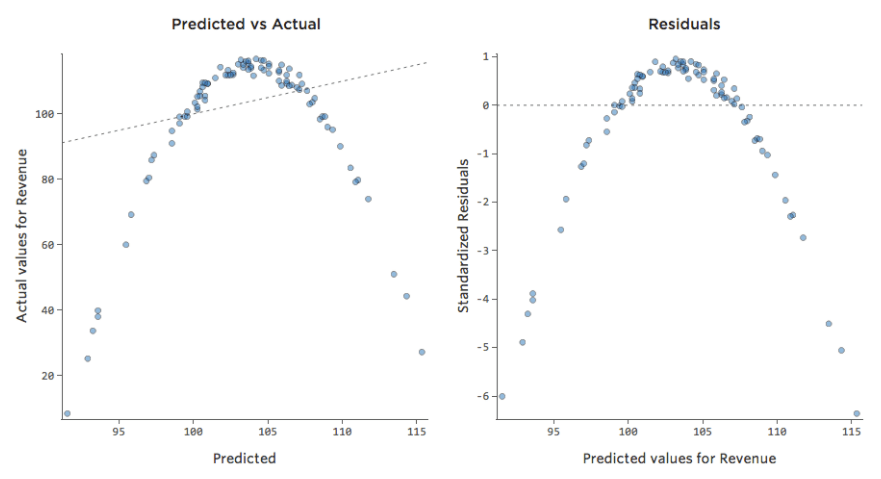
線で表されたモデルとはまったく異なります。予測は完全に外れています。つまり、モデルは「温度」対「収益」の関係を正しく表していません。
したがって、残差は以下のようになります。
影響
上の例のように、モデルが正しくないと予測は価値のないものになります(上記の0.027 R二乗のように、R二乗は非常に低くなります)。
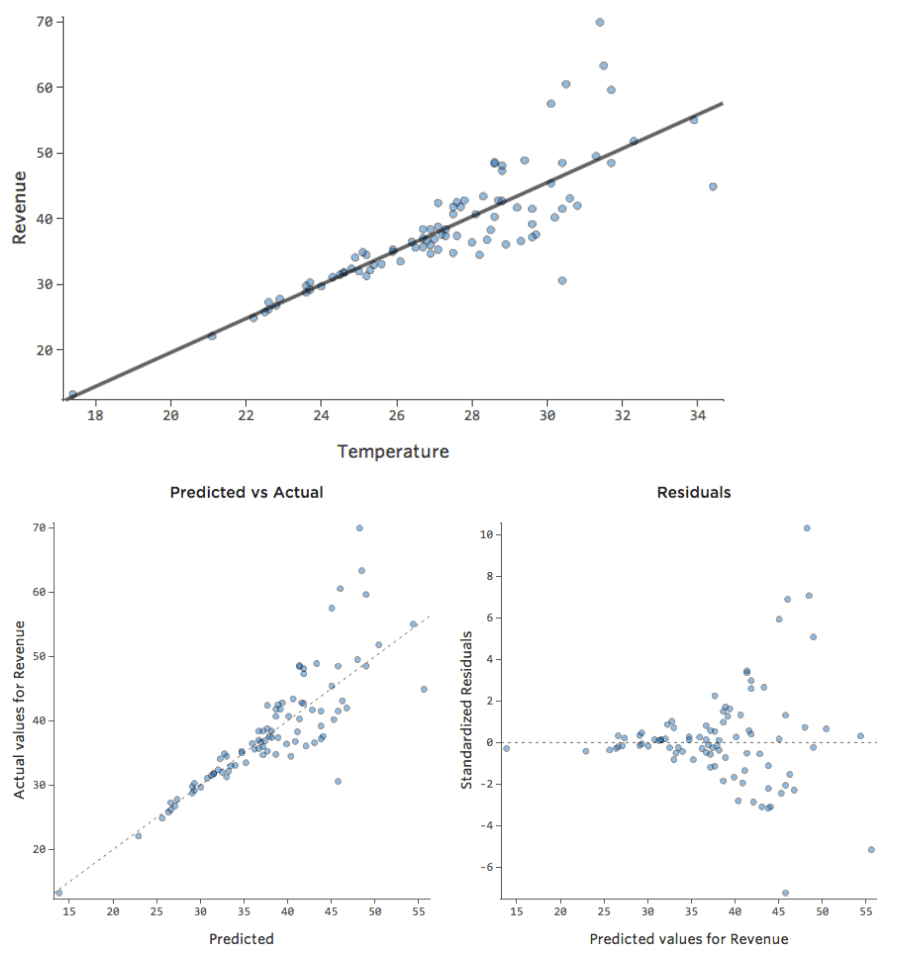
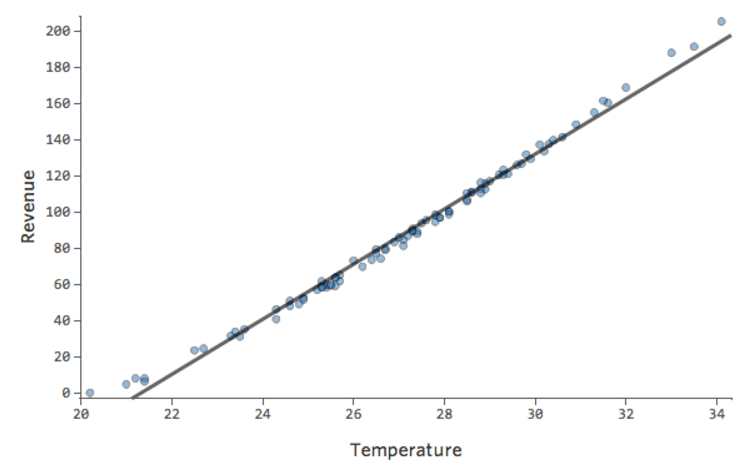
最適からやや外れる場合でも、完ぺきとは言えないまでも、以下のように関係性は感じ取れます。
このモデルはかなり正確に見えます。よく見ると(あるいは残差を見れば)、ここに少しパターンがあること、つまり線に一致しない曲線にドットがあることがわかります。
これは問題になるでしょうか。使用者次第です。関係についてすぐに理解できるなら、この直線はまずまずの近似です。このモデルを予測に使用し、説明を行わない場合は、最も正確なモデルはおそらくその曲線を考慮したものになるでしょう。
修正方法
- このようなパターンは、変数の変換が必要であることを示している場合があります。
- パターンが実際にこれらの例のように明確である場合は、非線形モデルを作成する必要があります (実際はそれほど難しくありません)。
- または、ここでも変数の欠落が問題である可能性もあります。
外れ値
- このプロットの詳細と修正方法を表示します。
-
問題
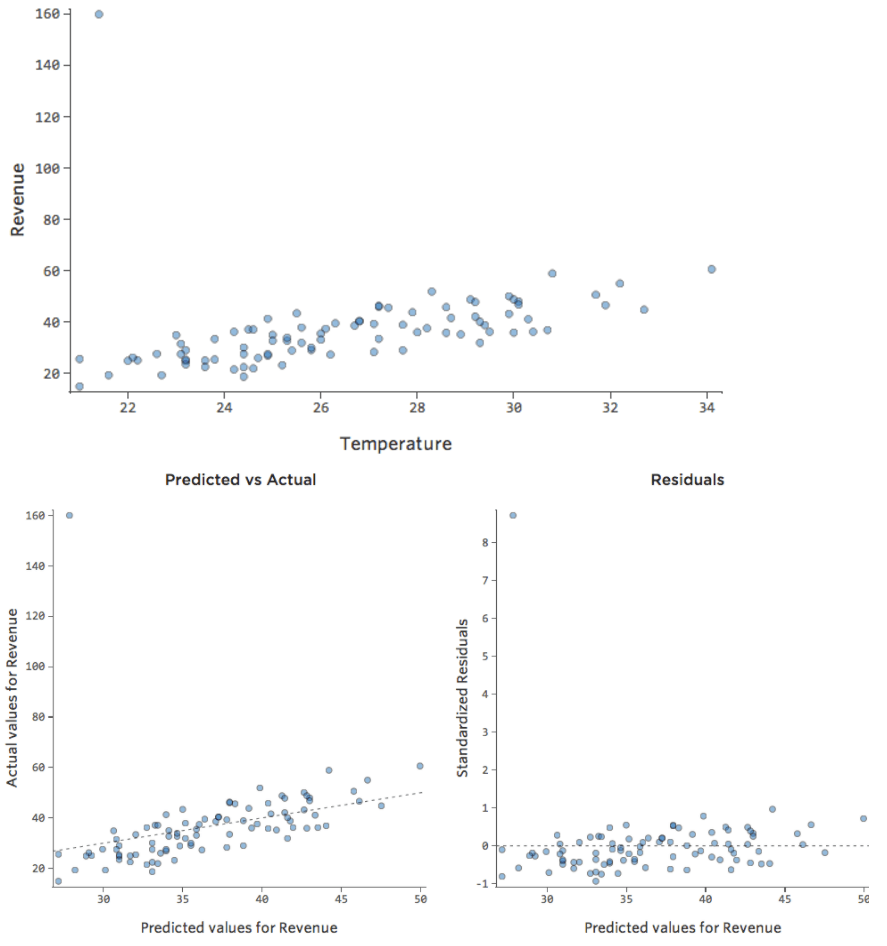
データポイントの1つに通常の20度台や30度台ではなく80という「温度」があったらどうでしょう?プロットは以下のようになります。
この回帰では、入力変数「気温」に外れ値のデータポイントがあります (入力変数の外れ値は「レバレッジポイント」 とも呼ばれます)。
データポイントの1つが、通常の20ドルから60ドルではなく160ドルの収益を得ていたらどうでしょうか。プロットは以下のようになります。
この回帰の出力変数「収益」には外れ値のデータポイントがあります。
影響
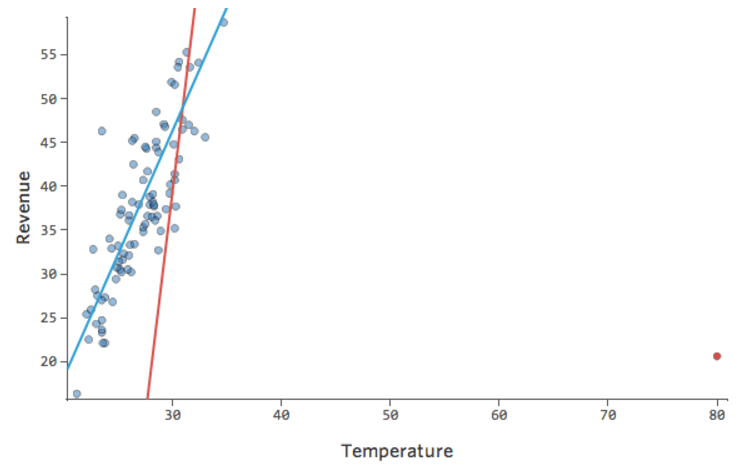
Stats iQは、通常、出力外れ値(売上160ドルの日など)の影響を受けないタイプの回帰を実行しますが、入力外れ値(80度台の「温度」など)には影響を受けます。最悪の場合、モデルがピボットして、そのポイントに近づこうとして他のポイントから離れ、以下のように完全に間違ったものになる可能性があります。
青い線はおそらく望ましいモデルの外観です。赤色の線は、80の「温度」の外れ値がある場合に表示される可能性のあるモデルです。
修正方法
- これは、外れ値が単なる誤りで、計測エラーまたはデータ入力エラーである可能性があります。その場合は外れ値を削除する必要があります。
- 2、3の外れ値だけに見えるのは、実はベキ分布である可能性もあります。変数の1つに非対称分布がある場合(ベル型でない)は、変数を変換することを検討してください。
- これが実際に正当な外れ値である場合は、その外れ値の影響を評価する必要があります。
Y軸の大きなデータポイント
- このプロットの詳細と修正方法を表示します。
-
問題
近くに2つの競合するレモネードスタンドがあるとします。ほとんどの場合、そのうち1軒のみが営業しているため、スタンドの収益は常に良好です。時折、どちらのスタンドも営業しておらず収益が急増することや、両方共営業していて収益が急減することもあります。
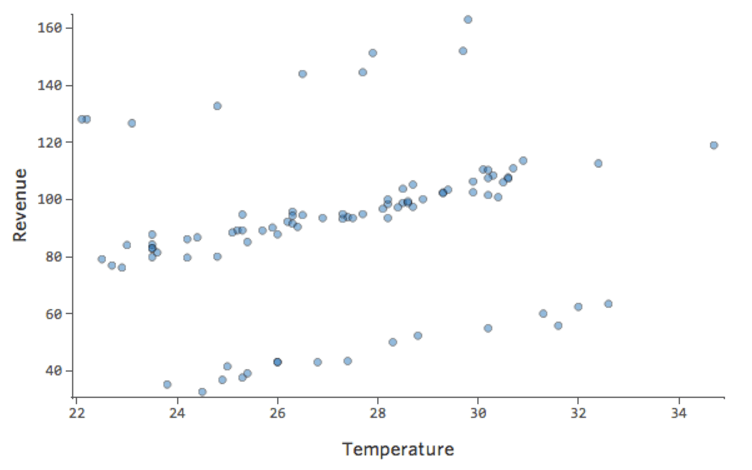
「収益」と「温度」は以下のようになります。
…上部の行は他のスタンドが営業していない日であり、下位の行は両方のスタンドが営業している日です。
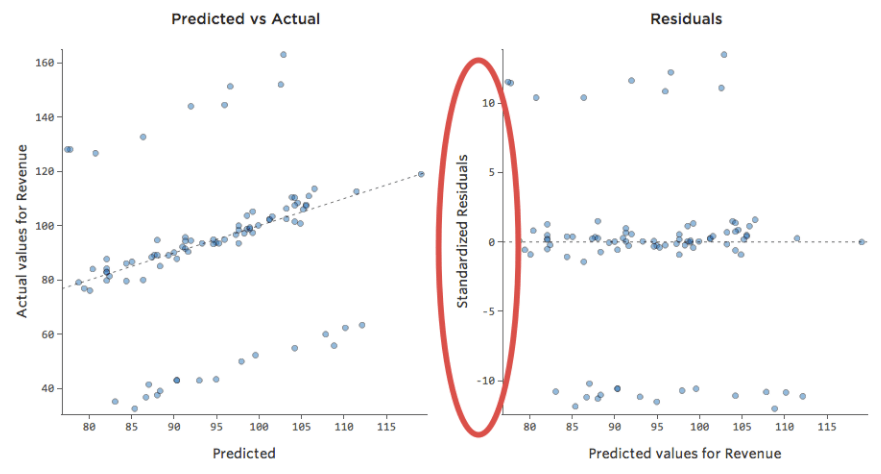
その結果、残差プロットは以下のようになります。
つまり、0の両側に10以上の残差があるデータポイントがかなり多くあり、これはモデルが外れているということです。
ここで、「営業しているレモネードスタンドの数」という変数のデータを毎日収集した場合、その変数をモデルに追加すると、この問題は解決されます。ただし、必要なデータがない場合や、必要な変数の種類について推測すらできない場合がよくあります。
影響
モデルに価値がないわけではありませんが、必要な変数がすべて揃っている場合ほど良いモデルではないことは間違いありません。このモデルを使用して、「このモデルはほとんどの場合かなり正確ですが、時折外れることがあります」と言うことはできるでしょう。これが役立つかについては、使用者の判断であり、モデルに基づいてどのような意思決定を行おうとしているかにかかっています。
修正方法
- このアプローチは、上のような特定の例では機能しませんが、変数を有効に変換する機会があるかどうかを確認する価値は常にあります。
- それでもうまくいかない場合は、欠落した変数の問題に対処する必要がある可能性があります。
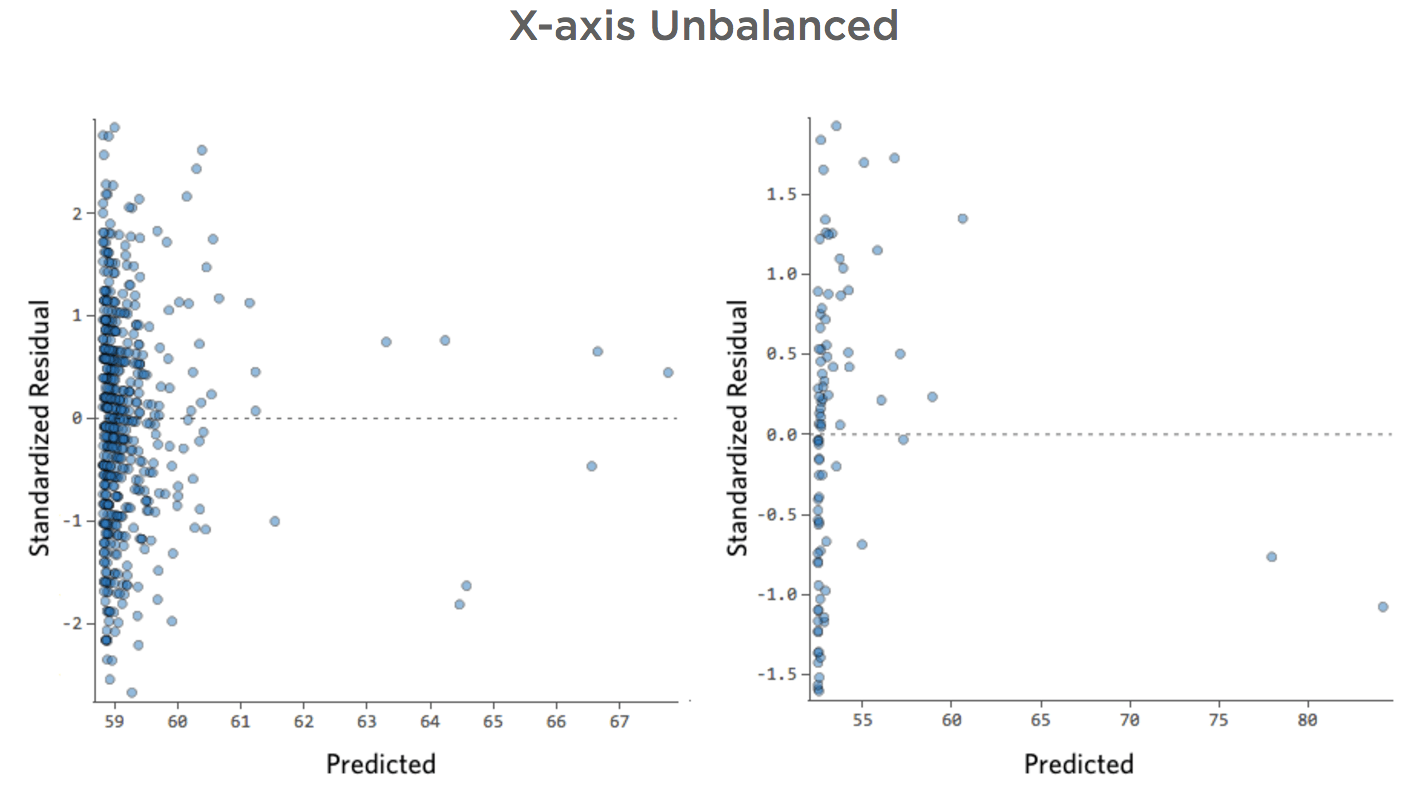
X軸が不均衡
- このプロットの詳細と修正方法を表示します。
-
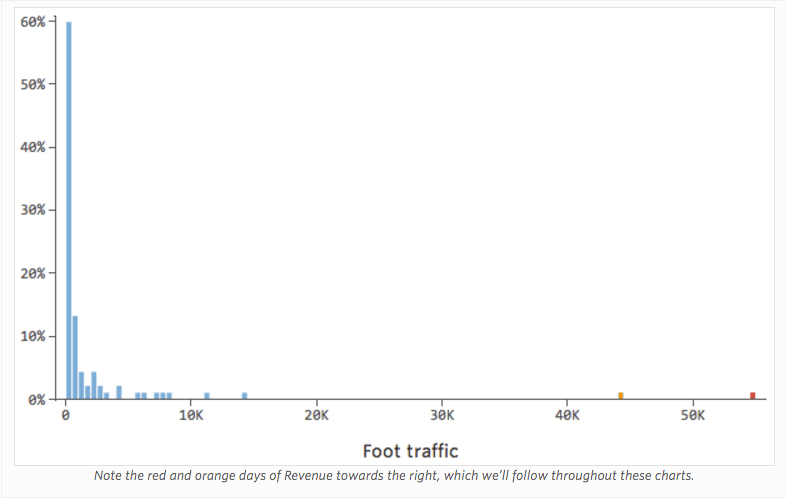
問題
「収益」は、「温度」に加え(または「温度]の影響はまったくなく)近隣の「交通量」に影響を受けていると想像してみてください。レモネードスタンドは、理由はどうあれ通常は収益が低く、時折、極めて収益が高い日がある場合もあるとします。その収益は以下のようになります。
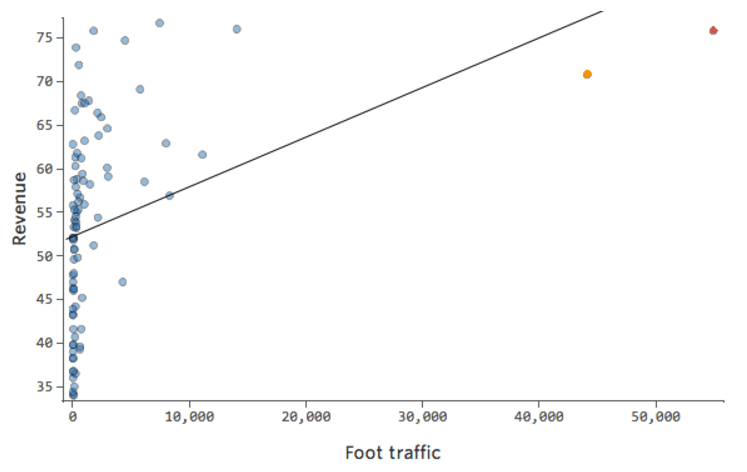
そのため「交通量」と「収益」は次のようになります。左側にほとんどのデータが固まっています。
黒い線は、モデル方程式、つまり「交通量」と「収益」の関係に関するモデルの予測を表します。このモデルでは、0と100または1,000の「交通量」の差異を正確に把握できていません。これらの値のすべてで、53ドル付近の収益が予測されています。
同じデータを診断プロットに変換します。
影響
モデルには実際には何も問題がない場合があります。上の例は良いモデルではありませんが、残差プロットが不均衡でもモデルはかなり良い場合もあります。
唯一の方法は、a) データの変換を試し、改善できるかどうかを確認し、b) 予測と実際のプロットを確認し、上記の例のように (ただし以下の例とは異なり) 多数のデータポイントで予測がうまく機能していないかどうかを確認することです。
残差が不均衡ではなく、正確であると言える明示的なルールはありません(実際にはこのモデルは非常に正確です)、X軸が不均衡な残差は、多くの場合、モデルに大幅な精度改善の余地があることを意味します。ほとんどの場合、モデルは方向性としては正しいものの、改善後のバージョンと比較するとかなり不正確であることがわかります。このような問題を修正した結果、モデルの R二乗が0.2から0.5(0から1のスケール) に跳ね上がることは珍しくありません。
修正方法
- この解決策は、ほとんどの場合データを変換することであり、通常は説明変数です。(下の例では回答変数の変換を参照しますが、こちらも同じプロセスが役に立ちます)
- モデルに変数が欠落している可能性もあります。
モデルの改善:外れ値の影響の評価
測定エラーやデータエラーではなく、正当な範囲外のデータポイントがあるとします。先に進む方法を決定するには、データポイントが回帰に与える影響を評価する必要があります。
これを行う最も簡単な方法は、現在のモデルの係数を書き留め、そのデータポイントを回帰から除外することです。モデルがあまり変わらない場合は、あまり心配する必要はありません。
モデルが大幅に変更された場合は、モデル (特に実績と予測) を検証し、どちらのモデルが適切であるかを判断します。理論的に説明できる限り、最終的に外れ値を捨てても問題ありません。「このケースでは、外れ値は関心の対象外です」、「それはジェリーおじさんが100ドル買ってチップをくれた日であり、予測不可能であり、モデルに含める価値はない」と考えます。
モデルの改善:変数の変換
概要
モデルを改善する最も一般的な方法は、1つまたは複数の変数を変換することです。通常、「ログ」変換を使用します。
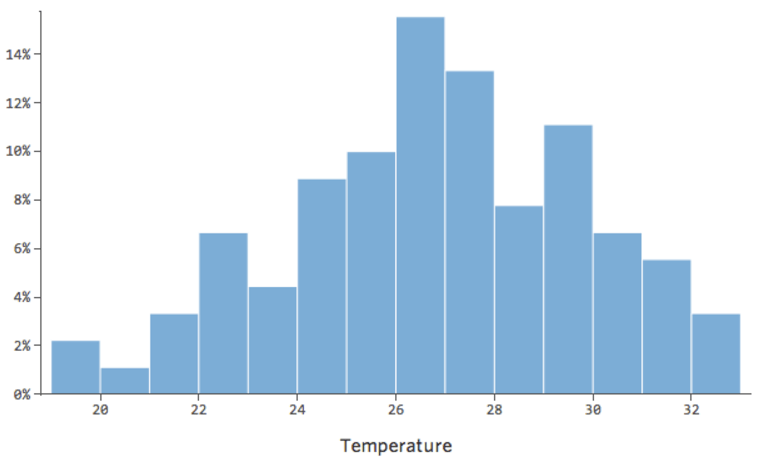
変数の変換によって、変数の分布の形が変わります。通常、開始するのに最適な場所は、より対称つまりベル型の分布ではなく、非対称分布を持つ変数です。そのため、次のような変数を見つけて変換します。
一般に、回帰モデルはより対称のベル型曲線において、より適切に機能します。さまざまな種類の変換を試して、その形に最も近いものを探り当ててください。近づけないことも多いですが、それが目標です。そこで、もっと対称的な形に近づけようとして「収益」に平方根をとると分布はこう見えます。
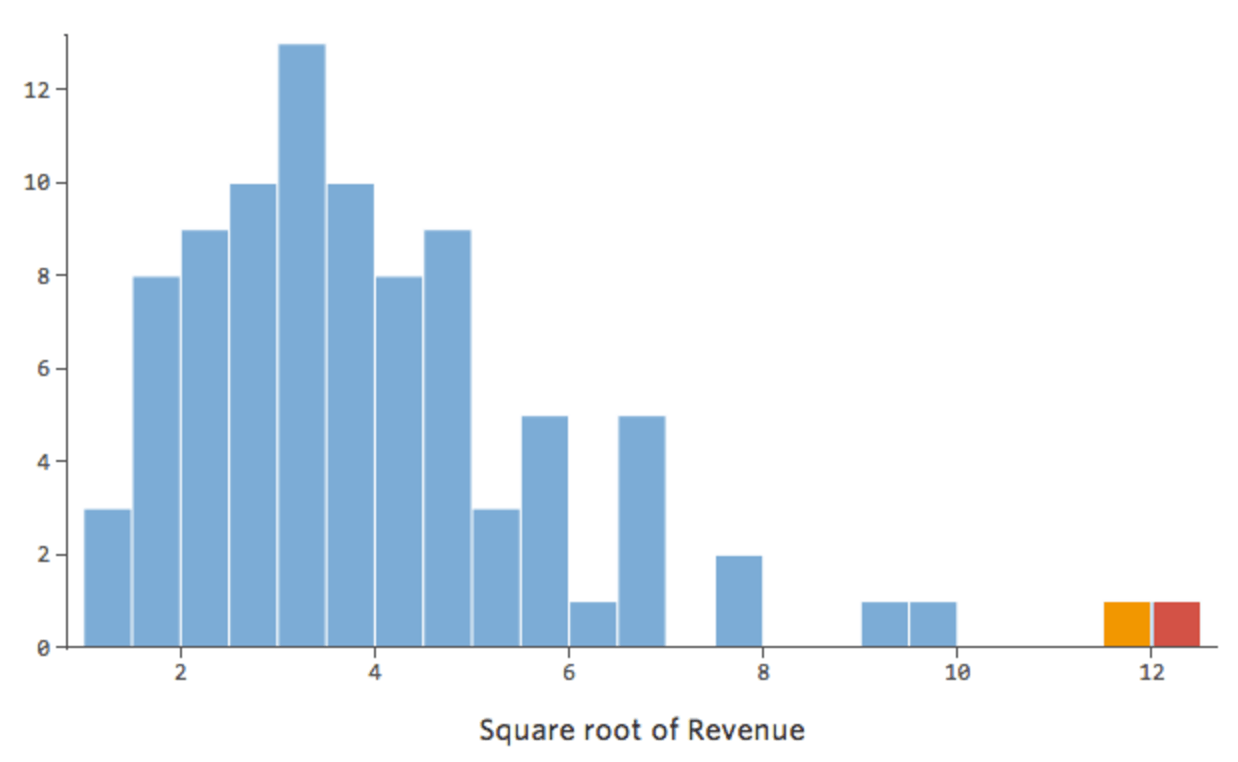
前よりいいですが、まだ非対称的です。代わりに「収益」のログを試してみると以下の形になります。
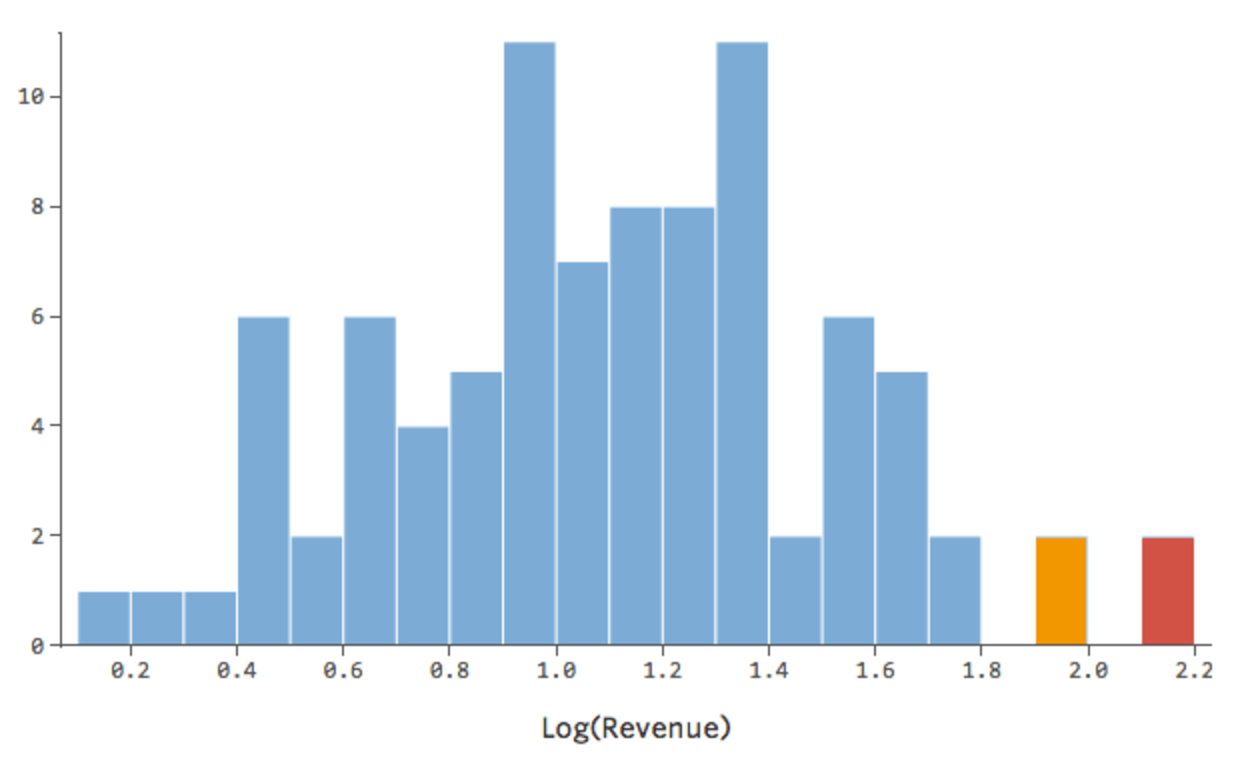
対称的になりました。「収益」ではなくlog (「収益」) を使用して、より適切な回帰モデルを得られる可能性があります。実際、方程式、残差、R二乗はどのように変化するかを示します。
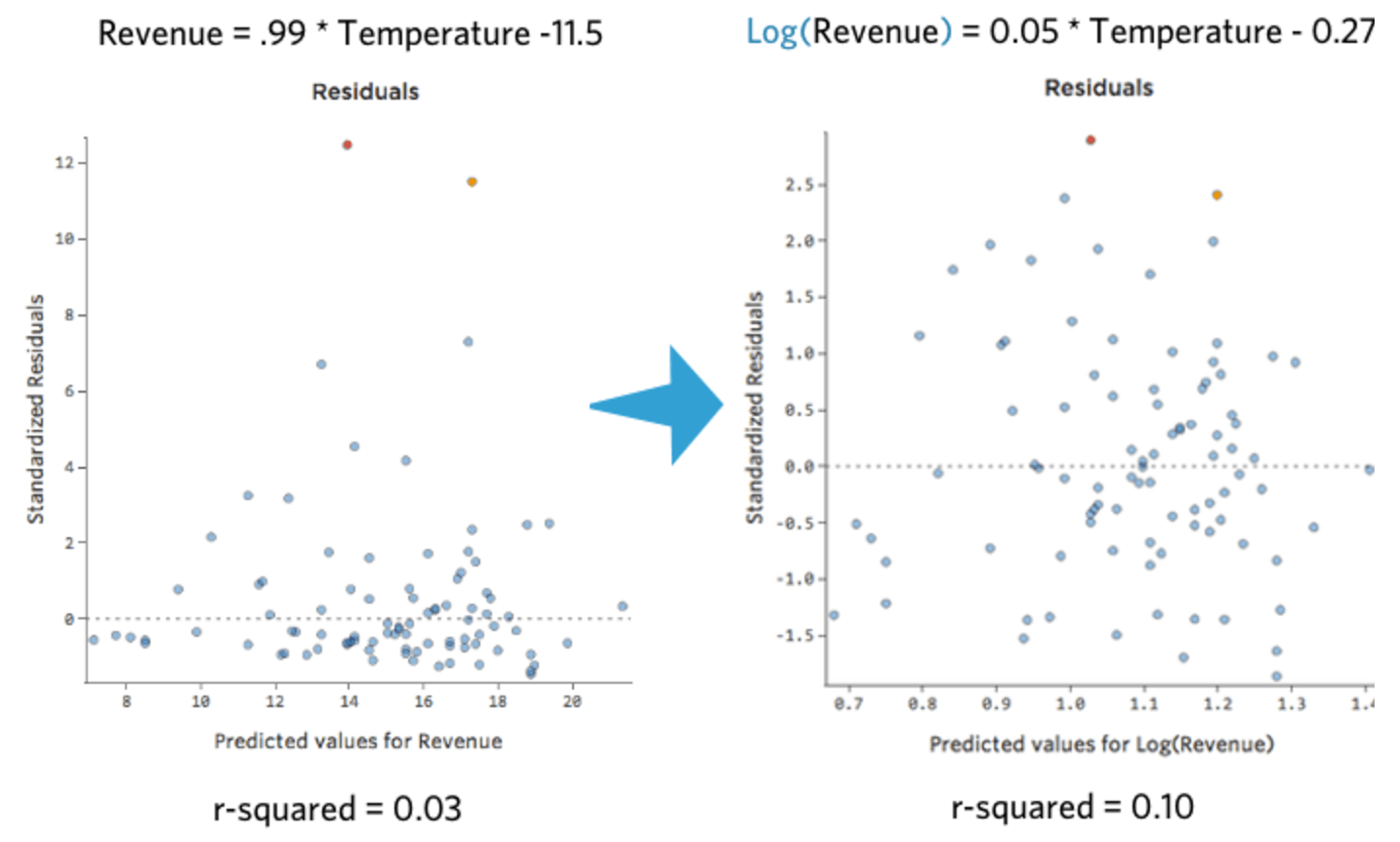
Stats iQでは、変数の分布の小さなバージョンがインラインで表示され、回帰方程式が示されます。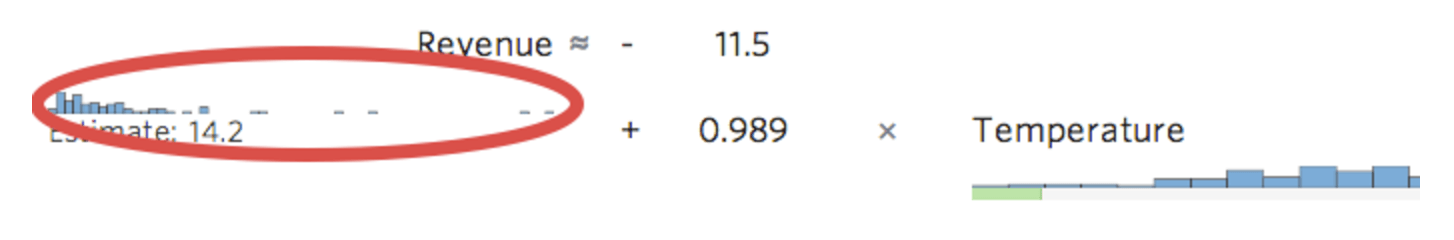
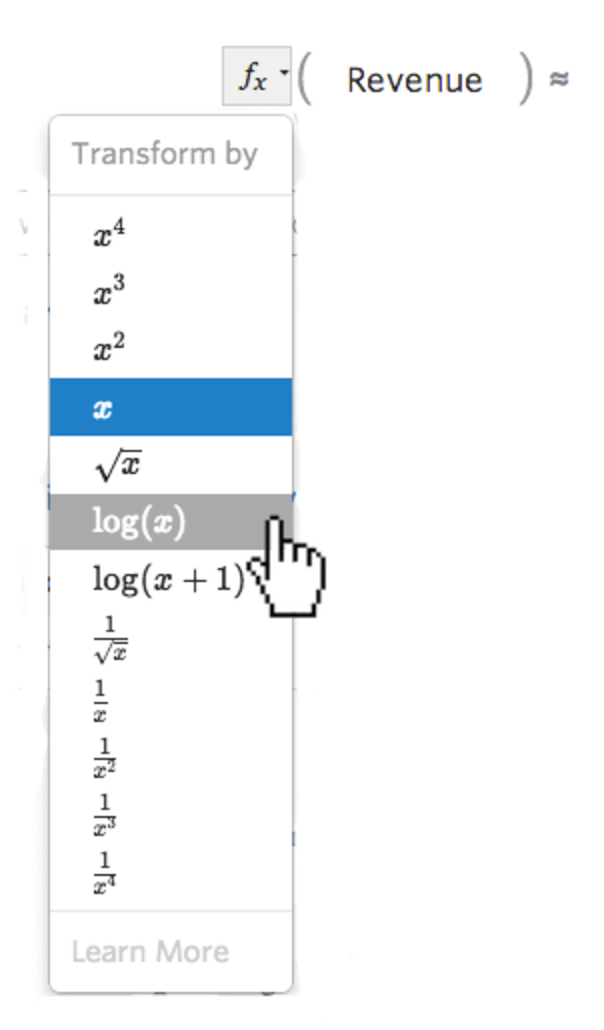
変数の左側にある変換 fx ボタンを選択します…
…次に変換を選択します。多くの場合、log(x)..です。
…次にヒストグラムを調べ、変換後のヒストグラムがより中央に集中しているかどうかを確認します。

変数を変換した後、変数の分布、回帰のR二乗、および残差プロットパターンがどのように変化するかに注意してください。これらが改善される場合 (特に、R二乗と残差)、変換を保持することが最善の方法です。
変換が必要な場合は、「ログ」変換から始めてください。これは、モデルの結果が理解しやすいためです。ただし、変換しようとしているデータにゼロまたは負の値が含まれている場合は、問題が発生します。ログの取得が非常に有用である理由、または変換する正でない数値がある場合や、データを変換するときに何が起こっているかをより深く理解するには、以下の詳細をお読みください。
詳細
数値のlog10() を取る場合、「10を何乗するとその数字になるか」を求めます。 たとえば、「収益」 と Log(「収益」) の両方を含む 4 つのデータポイントの簡単な表を次に示します。
| 温度 | 収益 | ログ (収益) |
|---|---|---|
| 20 | 100 | 2 |
| 30 | 1,000 | 3 |
| 40 | 10,000 | 4 |
| 45 | 31,623 | 4.5 |
「気温」対「収益」、「気温」対Log(“Revenue”)をプロットすると、後者のモデルの方がはるかに適切です。
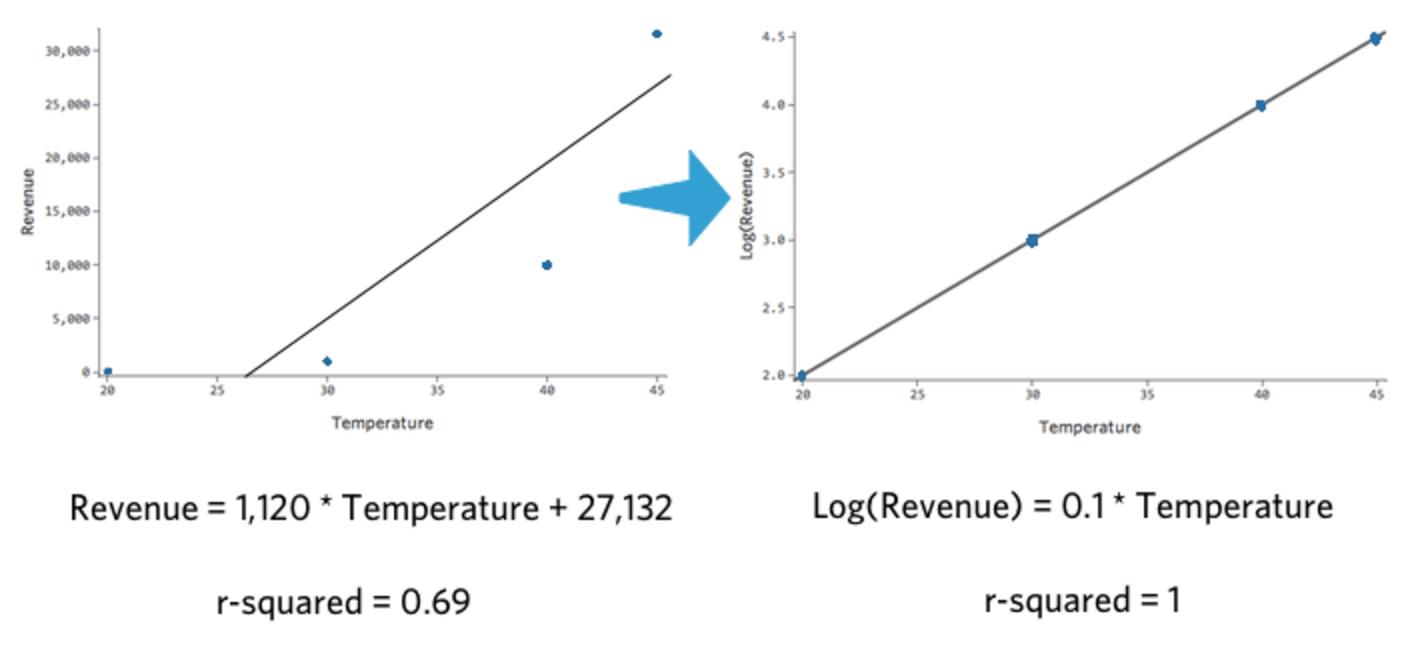
この変換で興味深いのは、回帰が直線的ではなくなったことです。「温度」が20から30になると、「収益」は10から100になり、90単位のギャップがあります。そのため「温度」が30から40になると、「収益」は100から1000となり、ギャップはさらに大きくなりました。
応答変数の対数を取った場合、「気温」の1単位の増加は「収益」のX–単位の増加ではなくなり、「収益」のX%の増加となりました。この場合、「温度」の10単位上昇は、Yが1000%上昇したことと関連しています。つまり、「温度」の1単位上昇は「収益」の26%の増加と関連付けられます。
また、ゼロや負の数の対数を取ることはできないことに注意してください(10X= 0や10X= -5 を満たすXは存在しません)。したがって、対数変換を行うと、このようなデータポイントは回帰分析から失われます。この状況を処理するには、以下の4つの一般的な方法があります。
- 平方根または立方根を取得します。これらは、ログを取るほど曲線の形を変えることはできませんが、回帰にゼロを残すことができます。
- ゼロのデータの行が多すぎず、これらの行が理論上重要でない場合は、ログの使用を続行し、回帰から数行を失ってもよいと判断できます。
- log(y) ではなく、log(y+1) を取り、0を1として回帰内に保持されるようにします。これによりモデルに少し偏りが生じますが、マイナスの副作用は通常、かなり軽微です。
モデルの改善:変数の欠落
モデルが適合しない最も一般的な理由は、適切な変数がすべて含まれていないことです。この特定の問題には、多くの解決方法があります。
新しい変数の追加
修正は、別の変数をモデルに追加するのと同じくらい簡単である場合があります。たとえば、週末のレモネードスタンドの「収益」のトラフィックが平日よりもかなり大きい場合、予測と実測のプロットは週末と平日の平均にちょうどかかっているため、下図のようになります (R二乗は 0.053)。
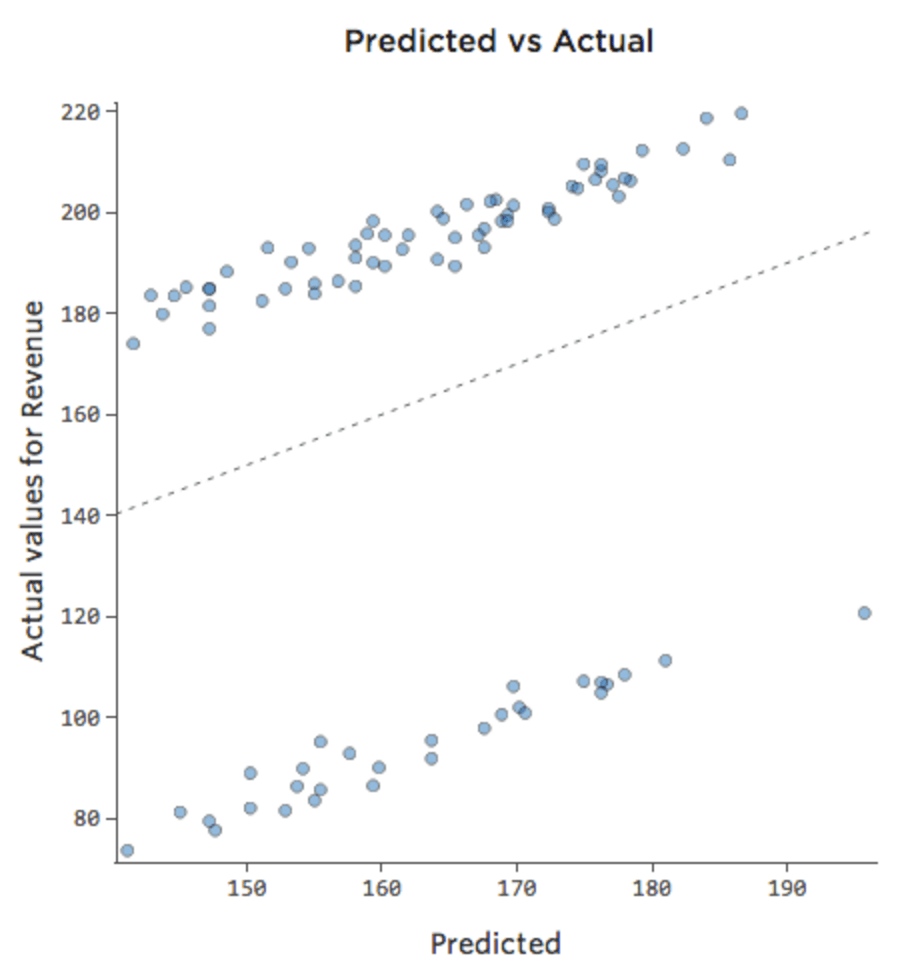
モデルに 「Weekend」(週末)という変数が含まれている場合、予測されたプロットと実際のプロットは、次のようになります (0.974 の R二乗)。
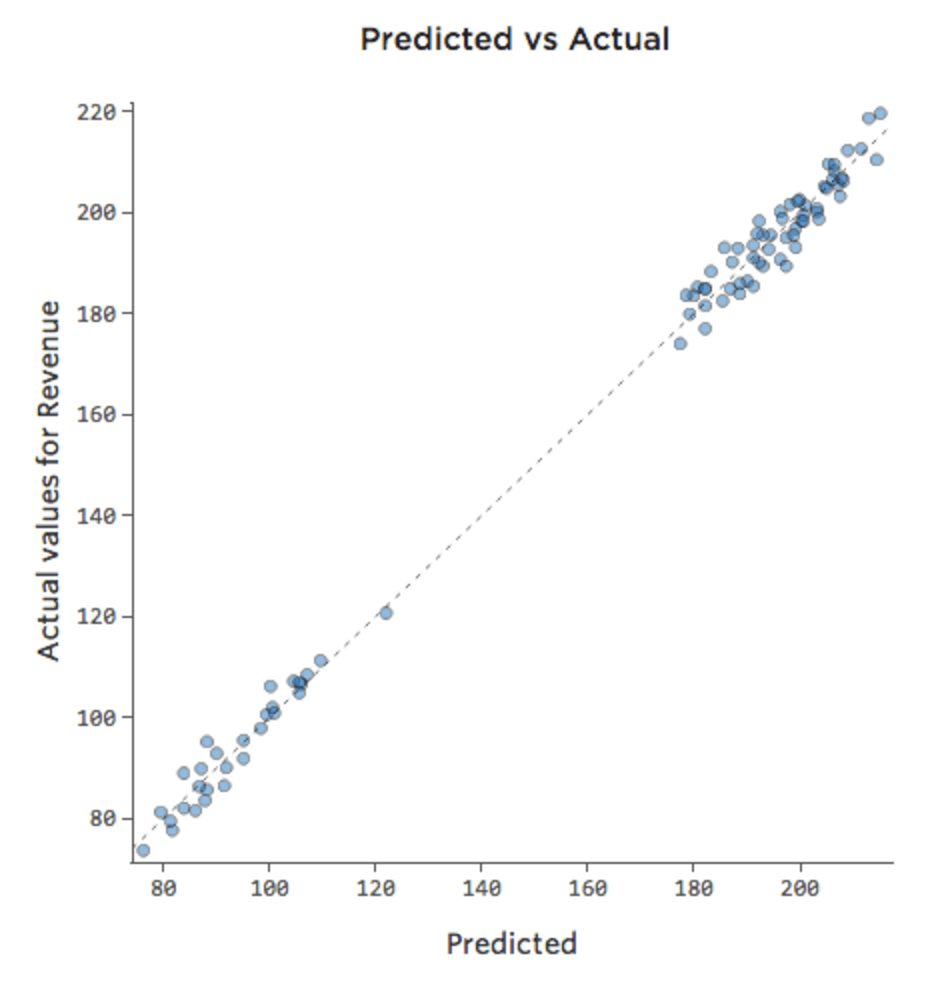
その日が平日であるかどうかを考慮できるため、モデルの予測はより正確になります。
この方法でモデルを改善するために、Stats iQで変数を作成する必要がある場合があります。たとえば、「日付」変数 (「10/26/2014」などの値を含む) があり、「曜日」(Sundayなど) または週末 (Weekendなど) という新しい変数を作成する必要がある場合があります。
利用できない省略された変数
それほど簡単ではない場合もあります。多くの場合、関連する変数が何であるかがわからないか、収集が困難でなため使用できません。週末対平日の問題ではなく、収集できなかった「エリア内の競合店舗数」のようなものである場合があります。
必要な変数が利用できない場合や、何が起こるかさえわからない場合、モデルを実際に改善することはできず、その変数を評価して、どの程度満足しているか(欠陥があっても有益かどうか)を判断する必要があります。
変数間の相互作用
週末にはレモネードスタンドは常に100%の販売力で販売しているため、「温度」に関係なく「収入」が高い。しかし平日はレモネードスタンドはそれほど忙しくないため、「温度」が「収益」の重要なドライバーとなる可能性があります。「週末」と「温度」を含む回帰を実行すると、このような予測と実測のプロットが表示される場合があります。上部にある行は週末日です。
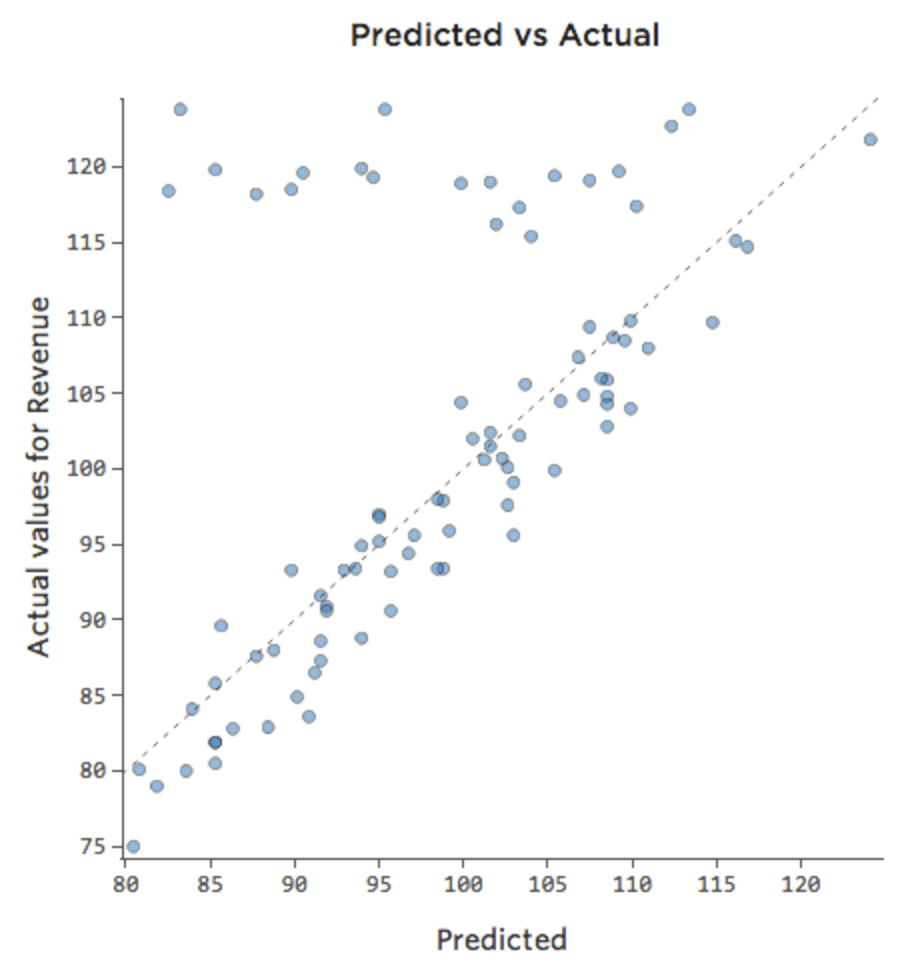
たとえば、「週末」と「気温」との間に相互作用があるとします。どちらか一方が「収益」に与える影響は、もう一方の値によって異なります。インタラクション変数を作成すると、より優れたモデルが得られます。この場合、予測値と実測値の比較は以下のようになります。
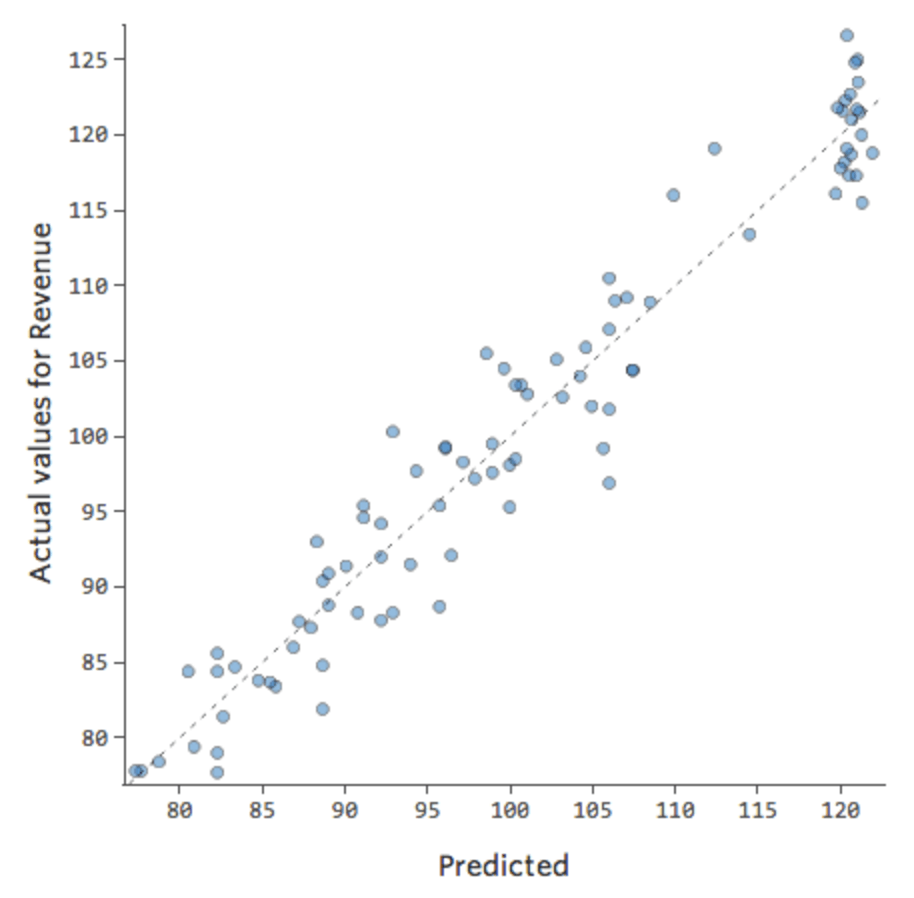
モデルの改善:非線形性の改善
たとえば、次のような関係があるとします。
形が放物線の形であることに気付くかもしれませんが、これは通常、次のような式に関連付けられています。
y = x2 + x + 1
デフォルトでは、回帰では次のような線形モデルが使用されます。
y = x + 1
実際、上のプロット内の線の式は次のとおりです。
y = 1.7x + 51
しかし、これはまったく適合しません。そのため、x2 項を追加すると、モデルは曲線に適合する可能性が高くなります。実際に作成するとこのようになります。
この曲線の式は次のとおりです。
y = -2x2 +111x – 1408
つまり、以下のような診断プロットから…
…こうなります。
これらの診断プロットは、データが右側に偏っているように見えても、健全な診断プロットであることに注意してください。
上記のアプローチは、x3項を加えることにより、他の種類の形状、特にS字型曲線に拡張できます。しかし、これは比較的珍しいと言えます。
以下の点に注意してください。
- 一般的に、データの非線形パターンのために x2 項がある場合は、x2ではなく普通のx項を使用します。なくても完全に良いとわかるかもしれませんが、必ず最初に両方を試してください。
- 回帰方程式を理解するのは困難かもしれません。このセクションの冒頭にある線形方程式では、「温度」が1単位増加すると「収益」は1.7単位上昇しました。方程式にx2 とxの両方がある場合、「温度が1度上がると何が起こるか」を説明するのは容易ではありません。そのため、方程式が十分に適合すると仮定して、線形方程式を使用する方が簡単である場合があります。