混乱マトリックスと精度と再現性のトレードオフ
混同マトリックスと精度-再現チャートは、モデルの精度を評価するのに役立ちます。
混同行列
例えば、リピーターになりそうな顧客には角砂糖を1個おまけしようと考えているとしよう。しかしもちろん、不必要に角砂糖を配ることは避けたいので、モデルが少なくとも30%の再来店の可能性があるとした顧客にのみ角砂糖を配る。
もし新しいお客さんが通りかかったら…。
| カスタマーID | 年齢 | 性別 |
|---|---|---|
| … | … | … |
| 324 | 54 | 女性 |
| 325 | 23 | 女性 |
| 326 | 62 | 男性 |
| 327 | 15 | 女性 |
| … | … | … |
…回帰モデルを使って、彼らが戻ってくる可能性を予測することができる。
| カスタマーID | 年齢 | 性別 | モデル推定によるリターンの可能性 |
|---|---|---|---|
| … | … | … | … |
| 324 | 54 | 女性 | 34% |
| 325 | 23 | 女性 | 24% |
| 326 | 62 | 男性 | 65% |
| 327 | 15 | 女性 | 7% |
| … | … | … | … |
…そして、少なくとも30%の可能性がある顧客を「再来店する」と分類し、角砂糖を渡すことにした:
| カスタマーID | 年齢 | 性別 | モデル推定によるリターンの可能性 | モデル予測 (30% カットオフ) |
|---|---|---|---|---|
| … | … | … | … | … |
| 324 | 54 | 女性 | 34% | 必ず戻る |
| 325 | 23 | 女性 | 24% | そうしない |
| 326 | 62 | 男性 | 65% | 必ず戻る |
| 327 | 15 | 女性 | 7% | そうしない |
| … | … | … | … | … |
我々のモデルの精度をよりよく理解するために、すでに持っているデータポイントにモデルを適用することができる。
| カスタマーID | 年齢 | 性別 | モデル推定によるリターンの可能性 | モデル予測 (30% カットオフ) |
返品 |
|---|---|---|---|---|---|
| 1 | 21 | 男性 | 44% | また来る | 返品 |
| 2 | 34 | 女性 | 4% | そうしない | 返品 |
| 3 | 13 | 女性 | 65% | 必ず戻る | そうではない |
| 4 | 25 | 女性 | 27% | そうしない | そうではない |
| … | … | … | … | … | … |
…そしてデータの正確さをアセスメントする。
| カスタマーID | 年齢 | 性別 | モデル推定によるリターンの可能性 | モデル予測 (30% カットオフ) |
返品 | 予測精度 |
|---|---|---|---|---|---|---|
| 1 | 21 | 男性 | 44% | また来る | 返品 | 正しい |
| 2 | 34 | 女性 | 4% | そうしない | 返品 | 不正解 |
| 3 | 13 | 女性 | 65% | 必ず戻る | そうではない | 不正解 |
| 4 | 25 | 女性 | 27% | そうしない | そうではない | 正しい |
| … | … | … | … | … | … | … |
…そして、それをさらに以下のカテゴリーに分類する:
- トゥルーポジティブ:モデルによって「復帰する」と分類され、実際に「復帰」していた。
- 偽陽性:モデルによって「戻ってくる」と分類されたが、実際には「戻ってこなかった」。
- トゥルーネガティブ:モデルによって「戻らない」と分類され、実際には「戻らなかった」。
- 偽陰性:モデルによって「戻らない」と分類されたが、実際には「戻った」。
| カスタマーID | 年齢 | 性別 | モデル推定によるリターンの可能性 | モデル予測 (30% カットオフ) |
返品 | 予測精度 | 精度タイプ |
|---|---|---|---|---|---|---|---|
| 1 | 21 | 男性 | .44 | 必ず戻る | 返品 | 正しい | トゥルー・ポジティブ |
| 2 | 34 | 女性 | .04 | そうしない | 返品 | 不正解 | 偽陰性 |
| 3 | 13 | 女性 | .65 | また来る | そうではない | 不正解 | 偽陽性 |
| 4 | 25 | 女性 | .27 | そうしない | そうではない | 正しい | トゥルーネガティブ |
| … | … | … | … | … | … | … | … |
最後に、これらの作業を精度と再現率にまとめることができる。
精度が高い:
- 帰国予定」とされた人のうち、実際に帰国した人の割合は?
- 真陽性/(真陽性+偽陽性)
リコールだ:
- 思い出してください:実際に「復帰」した選手のうち、そのように分類された選手の割合は?
- 真陽性/(真陽性+偽陰性)
ウェルビーイング・モデルは、精度と想起の値が高い。
- 精度94%(「復帰する」と特定されたほぼ全員が実際に復帰している)、再現率97%(「復帰した」と特定されたほぼ全員が復帰している)のモデルを想像してほしい。
- より弱いモデルは、精度が95%でも再現率が50%かもしれない(誰かを「戻ってくる」と特定した場合、それはほぼ正しいが、後に実際に「戻ってきた」人の半分を「戻ってこない」と誤認してしまう)。
- あるいは、精度が60%、再現率が60%のモデルかもしれない。
これらの数値は、実際に予測をすることがないとしても、あなたのモデルがどの程度正確であるかを知るのに役立つはずだ。
精密さvs. リコール曲線
一つのモデルの中で、精度と想起のどちらを重視するかを決めることもできる。角砂糖がとても足りないので、リピーターになってくれると確信が持てる人にだけ配ることにして、(30%ではなく)60%の確率でリピーターになってくれる顧客にだけ配ることにしたのかもしれない。
角砂糖を配るのは、誰かが “必ず戻ってくる “と本当に確信したときだけだから、私たちの精度は上がる。最終的に “リターン “した人の中には、角砂糖を渡すほど自信がなかった人もたくさんいるだろうから、私たちのリコールは下がるだろう。
精度:62% ->80%リコール
: 60% ->30%
角砂糖でリッチな気分を味わうなら、リターナーになる確率が10%以上の人に配ることもできる。
精度: 62% -> 40%再現率
: 60% ->90%
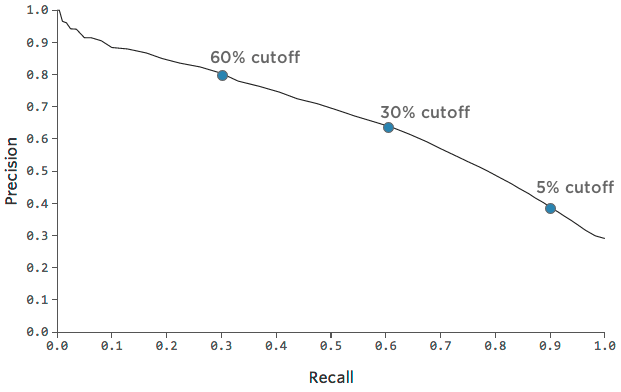
この精度と想起のトレードオフをこのチャートでたどることができます:
チャート上で精度とリコールがうまくミックスされたポイントを選び、そのポイントでモデルがどの程度正確であるかを把握することは有用である。