記事テンプレート

回帰と相対的重要性について

回帰は、複数の入力変数が一緒になって出力変数にどのような影響を与えるかを示す。例えば、”顧客としての年数 “と “企業規模 “の両方のインプットが、”顧客満足度 “というアウトプットと互いに相関している場合、回帰を使って、2つのインプットのどちらが “顧客満足度 “の作成に重要かを調べることができる。

相対重要度調査は、アンケート調査の回帰分析のベストプラクティスであり、Stats iQで行われる回帰分析のデフォルト出力です。相対重要度は、入力変数が互いに相関している状況をアカウントする回帰の最新の拡張であり、アンケート調査では非常に一般的な問題です（「多重共線性」として知られています）。相対的重要度は、ジョンソンの相対的重み設定としても知られ、シャプレー分析のバリエーションであり、支配力分析と密接に関連している。

Stats iQでの回帰の設定方法については、下記をご参照ください。回帰分析の分析的な部分を考え抜くためのガイダンスについては、以下のページを参照してください：

• 線形回帰のユーザーフレンドリーなガイド
• 線形回帰を改善するための残差プロットの解釈
• ロジスティック回帰の使いやすいガイド
• ロジスティック回帰におけるコンフュージョンマトリックスと精度と再現性のトレードオフ

Qtip: Stats iQプラットフォームに便利なツールチップが追加されました！Stats iQで作業中、プラットフォーム全体に表示されるiアイコンを クリックすると、追加情報や定義が表示されます。

線形回帰については、Stats iQのRelative Importanceは、Lipovetsky, Stan & Conklin, Michael.(2001). ゲーム理論的アプローチによる回帰分析。ビジネスと産業における適用確率モデル。 17.319 – 330. 10.1002/asmb.446.

回帰カードの変数の選択

回帰カードを作成すると、データセット中のある変数の値が、他の変数の値によってどのように影響されるかを理解することができます。

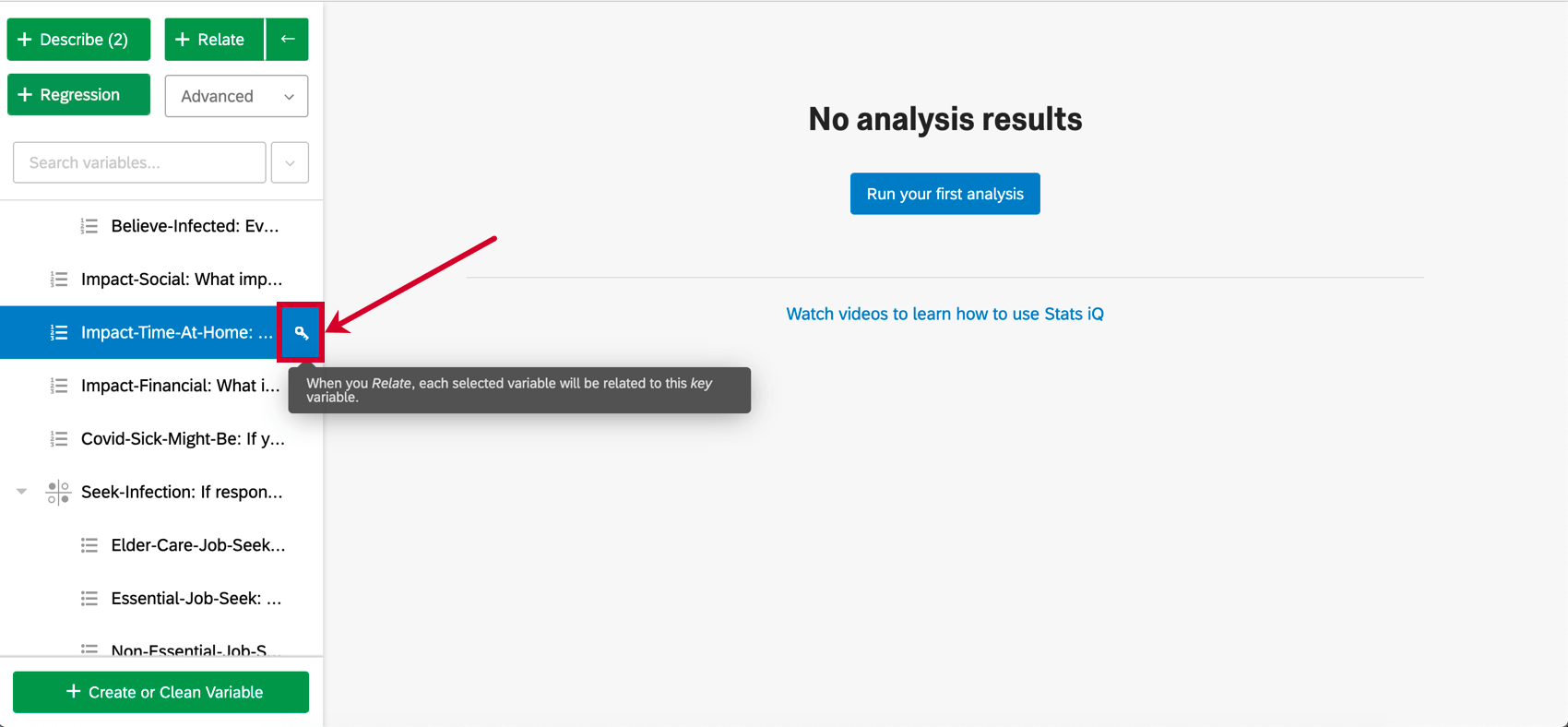
変数を選択するとき、ある変数にはキー変数が付く。回帰では、キー変数が出力変数になります。キー変数の後に選択された他の各変数は、入力変数となる。言い換えれば、出力変数の値が入力変数によってどのように左右されるかを説明しようとしているのだ。

回帰のための変数を選択するときに考慮すべきこと：

• 変数ペインの任意の変数の次へキーアイコンをクリックすることで、キー変数を変更できる。
• 回答数よりも多くの変数が選択されている場合、回帰は実行されません。
• 入力変数は最大25個まで選択できる。しかし、1～10個の入力変数を選択するようにしなければ、結果が非常に複雑になる可能性がある。

分析に含めたい変数の数が多い場合は、以下のアプローチを検討する：

• いくつかの初期回帰を実行し、モデルにおいてほとんど重要でない変数を除外する。
• 複数の変数を平均化するなどして組み合わせる。
• データの構造上それが可能であれば、341ページで説明されているように、2段階の相対的重要度プロセスを使用することができる。

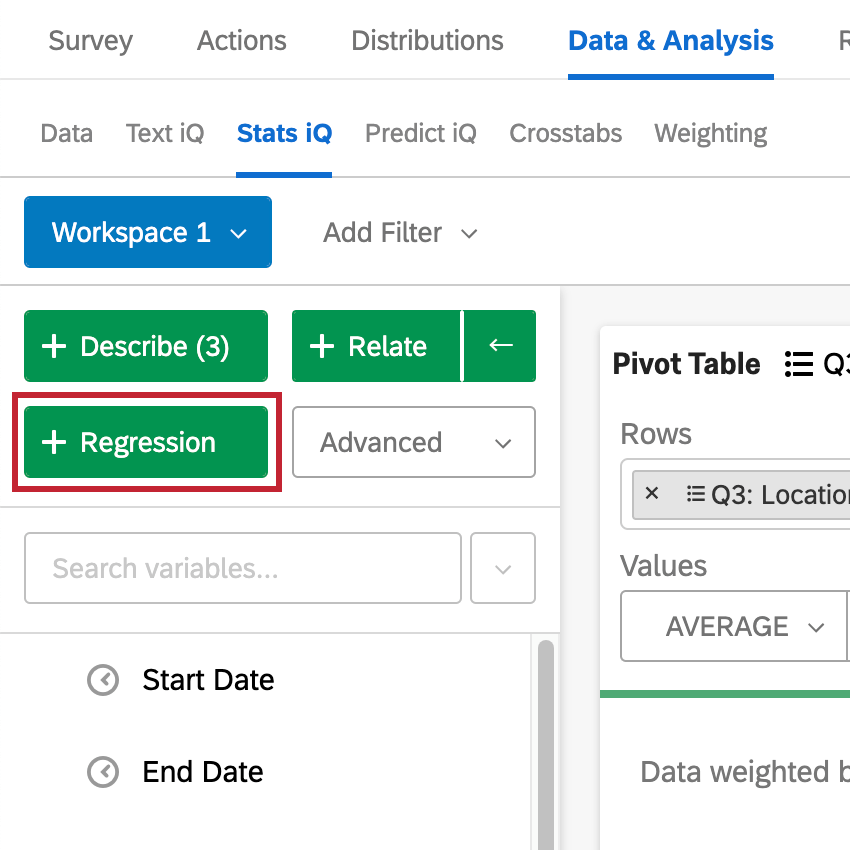
変数を選択したら、回帰をクリックして回帰を実行します。

回帰の種類

Stats iQで実行される回帰には、主に2つのタイプがあります。出力変数が数値変数の場合、Stats iQは線形回帰を実行します。出力変数がカテゴリー変数の場合、Stats iQはロジスティック回帰を実行します。

より具体的には、Stats iQが実行する回帰のタイプは以下の通りです：

線形回帰

相対的重要度を最小二乗法（OLS）と組み合わせる。出力は2つの分析を組み合わせたものである：

• 相対的重要度．このセクションのすべては，OLS回帰に由来するr2乗を除いて，Relative Importanceに由来する．
• モデルを詳しく調べるこのセクションのすべては，データ自体から抽出された配信を除いて，Relative Importanceから来ている．
• モデルを改善するためにOLS回帰の診断と残差を分析します：このセクションのすべては、OLS 回帰から来ています。

ロジスティック回帰

ロジスティック回帰は、入力変数の集合を与えられたバイナリ（たとえば、Yes または No）の結果のドライバーを理解するために使用されるバイナリ分類手法である。2つ以上のグループを持つ出力変数で回帰を実行すると、Stats iQは、バイナリ回帰になるように、1つのグループを選び、他のグループを一緒にバケットします（回帰を実行した後で、どのグループを分析するかを変更できます）。

相対的重要性

アンケート調査の入力変数は、互いに高い相関があることが多く、これは “多重共線性 “と呼ばれる問題である。これは、ある変数の重要性を人為的に増加させ、別の相関変数の重要性を減少させる回帰出力につながる可能性がある。相対的重要度（Relative Importance）は、これをアカウントするためのベストプラクティスの方法として認識されている。

相対重要度（特にジョンソンの重み設定）は，この問題に悩まされず，実行される回帰の変数タイプに関係なく，入力変数の重要度のバランスを適切にとる．それはまた、各変数の相対重み設定（または相対重要度）、つまりその変数によるアウトプットの説明可能な変動の割合を計算する。これは、100％に加算される一連のパーセンテージとして表示される。

それは、入力変数のバリエーションごとに、一連の回帰を実行するのと同じような結果を返します。例えば、2つの変数があった場合、Itは3つの回帰を実行するのと同じことになる：1つは変数A、もう1つは変数B、そしてもう1つは両方である。これは、各変数の重要性を定量化し、その定量化を回帰結果に適用することを可能にする。

回帰出力

Stats iQで回帰を実行すると、分析結果には以下のセクションが含まれます：

数値の概要

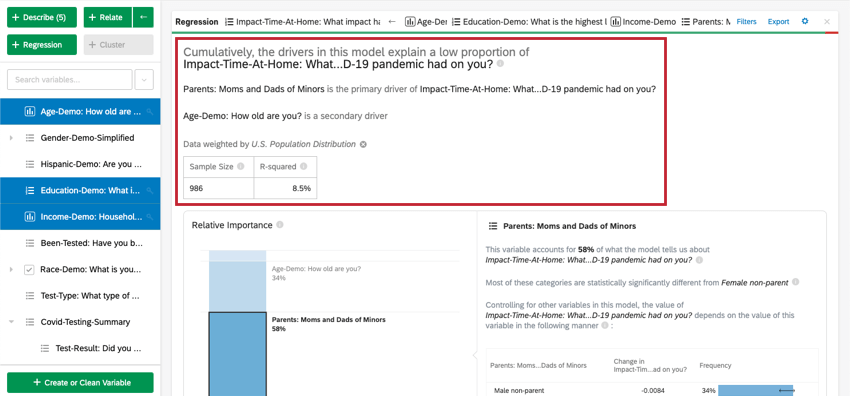
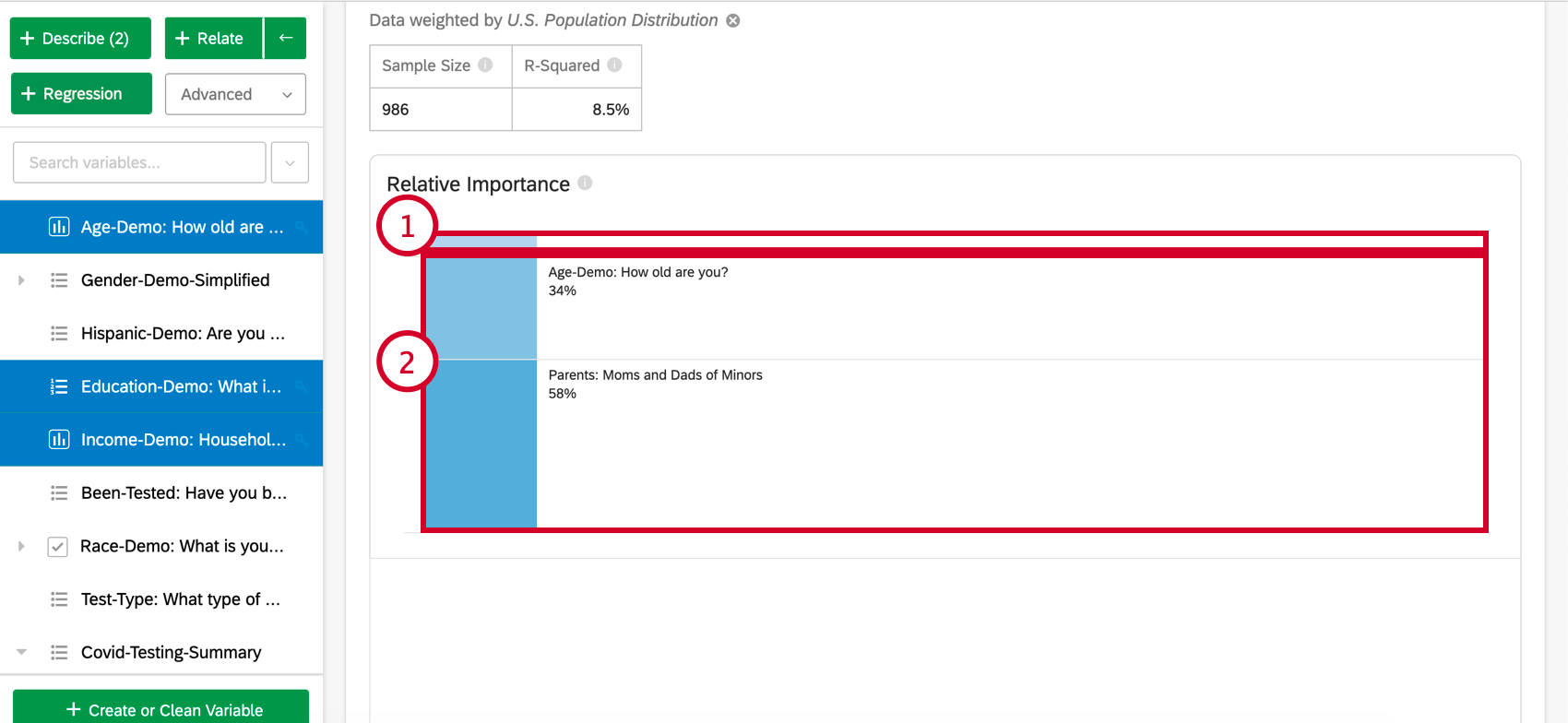
カードの上部には回帰分析の要約がある。選択された変数を見て、この要約書は、どの変数が主要なドライバーなのか、二次的なドライバーなのか、また累積的なインパクトが低いドライバーなのかを説明している。データテーブルには、サンプルサイズとR2乗値が含まれている。

相対的重要性

1. 影響度の低い変数：個々の相対的重要度が10％以下の変数はグループ化される。選択されると、各低影響変数の相対的重要度と統計的有意性を説明するセクションがある。
2. インパクトの高い変数：各インパクトの高い変数は分離され、クリック可能になります。変数が選択されると、棒グラフの下に、説明された変動と、モデルで他の変数がコントロールされた場合にどうなるかを見ることができます。

その他のモデル詳細

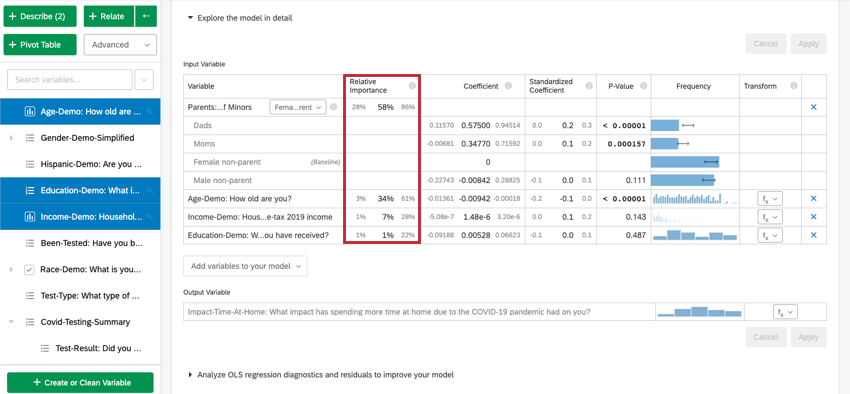
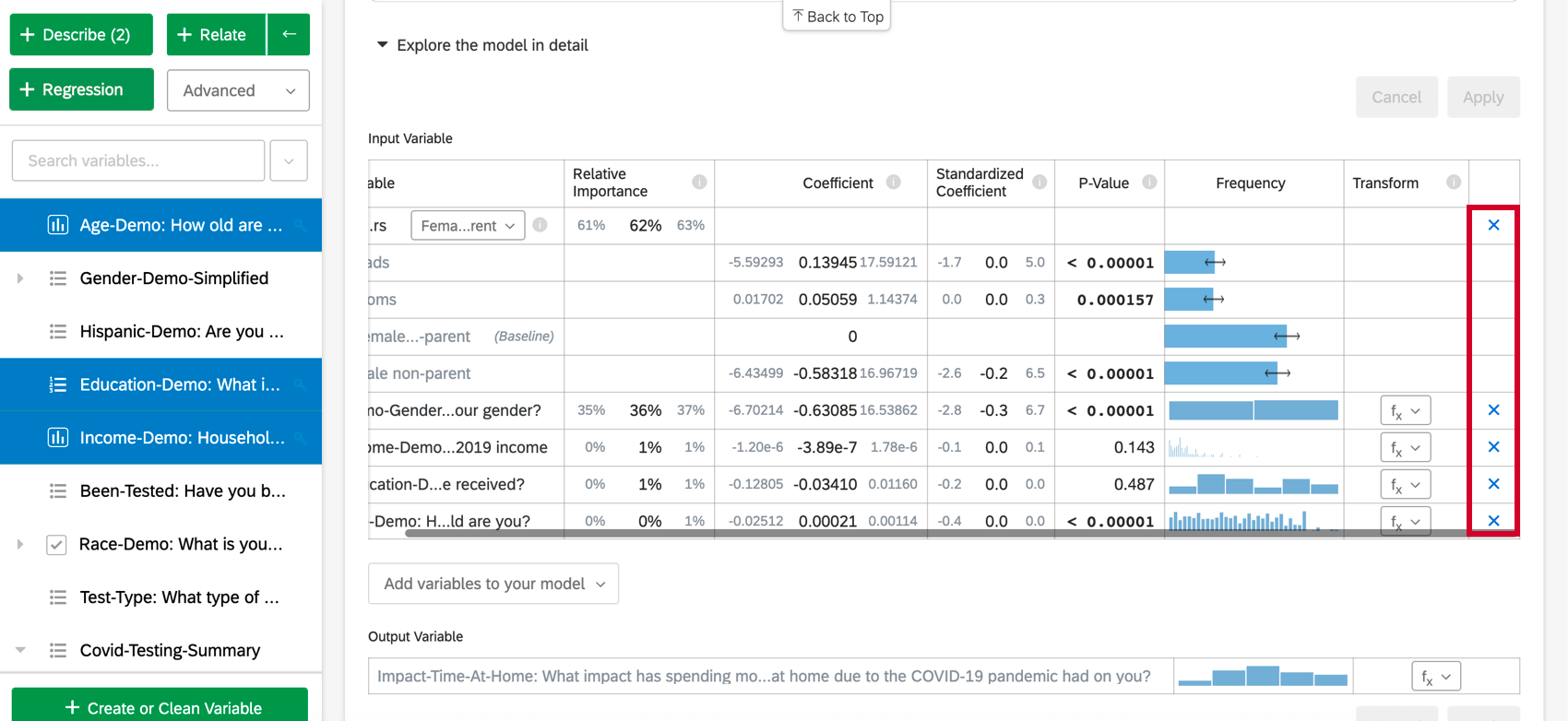
モデルを詳細に探索するを選択すると、入力変数と出力変数がリストされます。入力変数には以下の情報が含まれています：

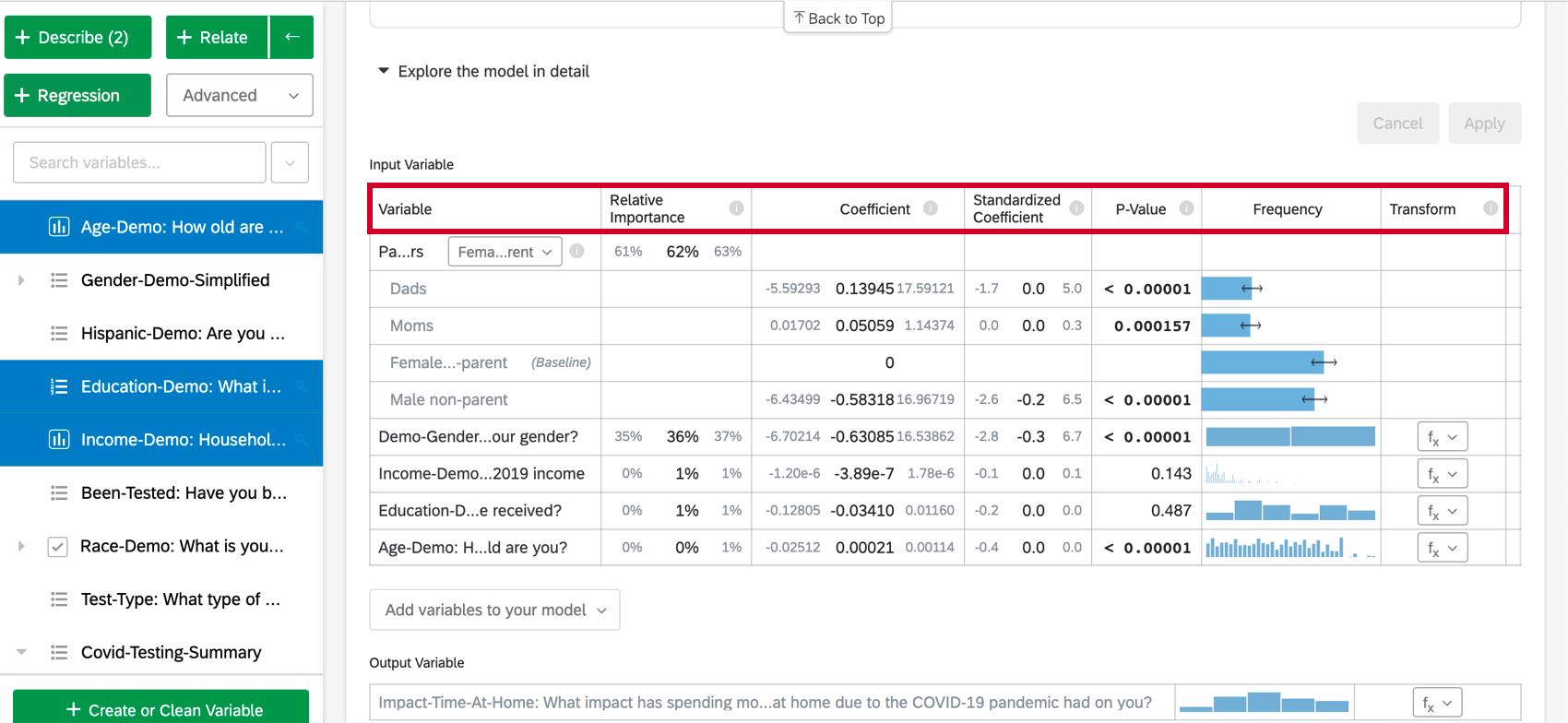
• 相対的重要度．個々の変数によって寄与されるr2乗の比率．r 乗は、このモデルの入力変数によって説明できる結果変数の変動の割合である。詳しくは相対的重要度を参照。
• オッズ比：ロジスティック回帰にのみ関係する。与えられた入力変数のオッズ比は、説明変数が1単位増加するごとにオッズが変化する係数を示す。
  例 たとえば、マネージャーとの満足度（Satisfaction with Manager）のオッズ比が1.1で、出力変数のグループが満足（Satisfied）と満足（Not Satisfied）である場合、マネージャーとの満足度（Satisfaction with Manager ）が1高いすべてのインスタンスについて、満足（Satisfied）の出力変数のオッズは1.1高い（10%高い）。 データの行がcolor[blue]のようなCategoryの場合、係数は、Categories変数が “ベースライン “グループ（赤、緑など）の代わりにその特定のCategory（青）である場合の応答変数のオッズの変化を表します。
• 係数：入力変数が1単位増加するごとに、出力変数の係数が増加する。これらの係数は、相対重要度分析の結果に基づいて構成されているため、多重共線性を調整しており、標準的な最小二乗回帰から得られる係数とは一致しない。
• 標準化係数．標準化係数は，係数を入力変数の分散で区切ったものである．これにより、各変数を同じ尺度に置き、係数をより直接的に比較することができる。
• P値：P値は統計的有意性の尺度である。値が低いほど、関係が偶然である確率が低い。カテゴリー変数については、P値は、その変数におけるグループと「ベースライン」グループとの差の統計的有意性を示す。
• 変換する：変数を変換する」を参照。

OLS回帰の分析

線形回帰の場合は、キー変数/出力変数の下にあるモデルを改善するための OLS 回帰診断と残差の分析をクリックして、予測対実際と残差のプロットを表示します。詳細は、回帰を改善するための残差プロットの解釈を参照してください。

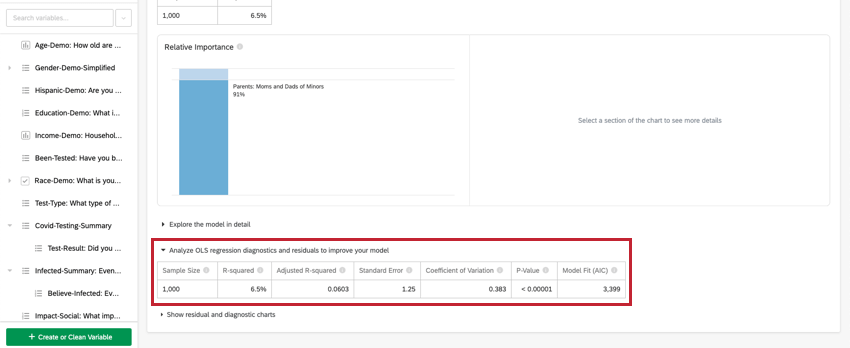
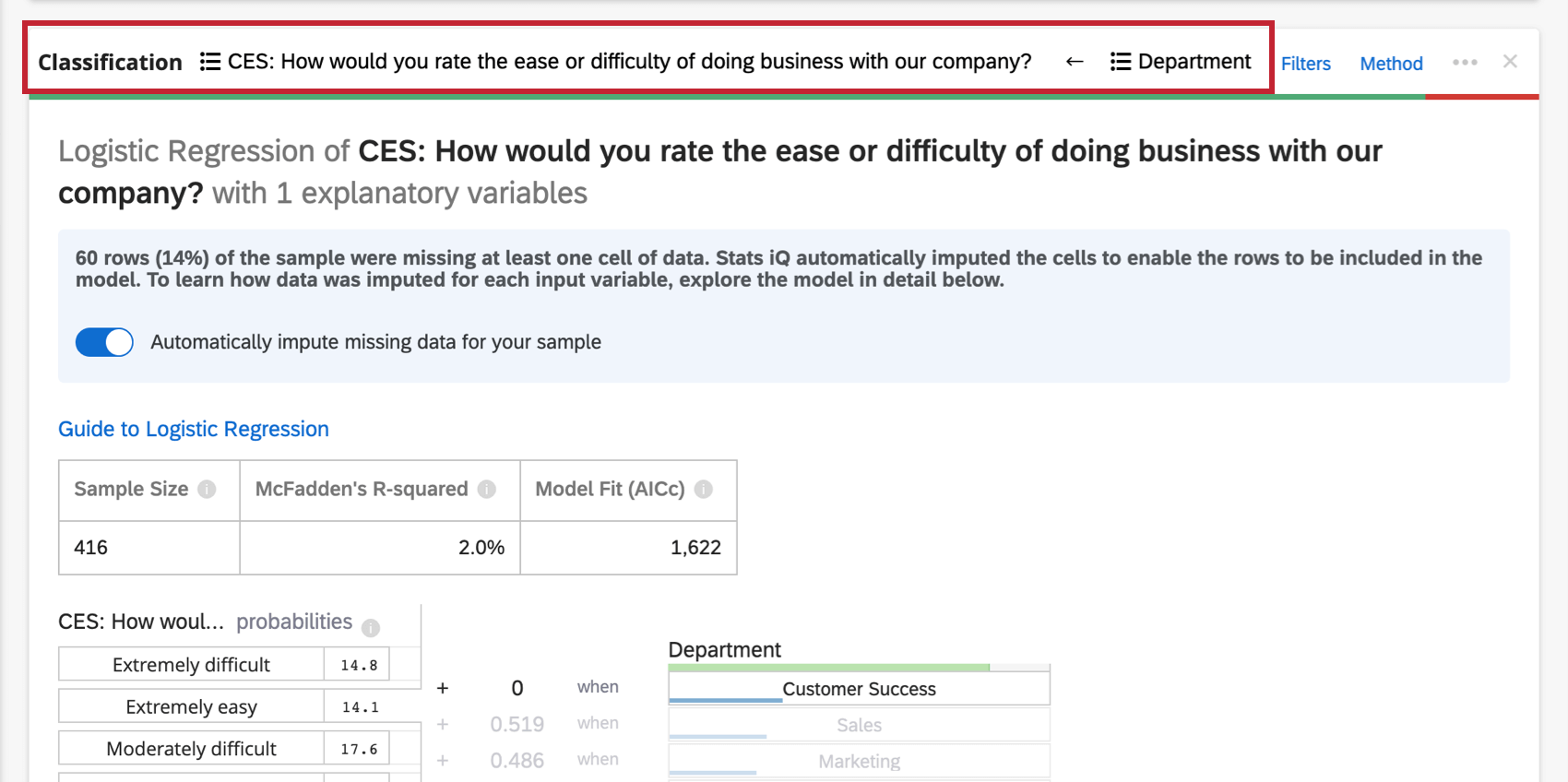
変数が含まれる

回帰カードの一番上のヘッダーに沿って、回帰で使用される変数が表示されます。

変数名をクリックすると、識別値を割り当てたり、バケットしたりできる新しいウィンドウが開きます。矢印をクリックして、分析の入力変数と出力変数を切り替えます。

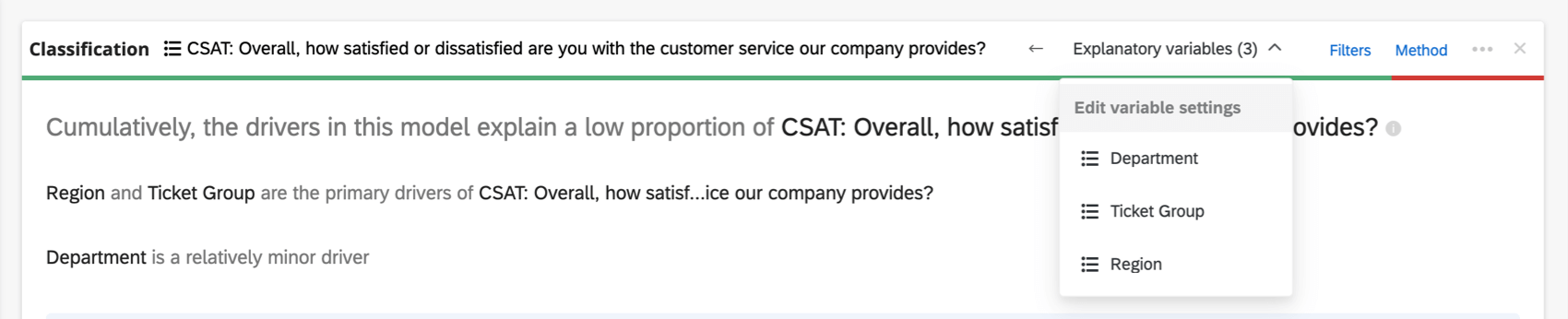
ヘッダーに表示する変数が多すぎる場合は、説明変数のドロップダウンがあり、再コード化したい変数を選択することができます。

変数の追加と削除

回帰カードを作成したら、以下の手順で分析に変数を追加できます：

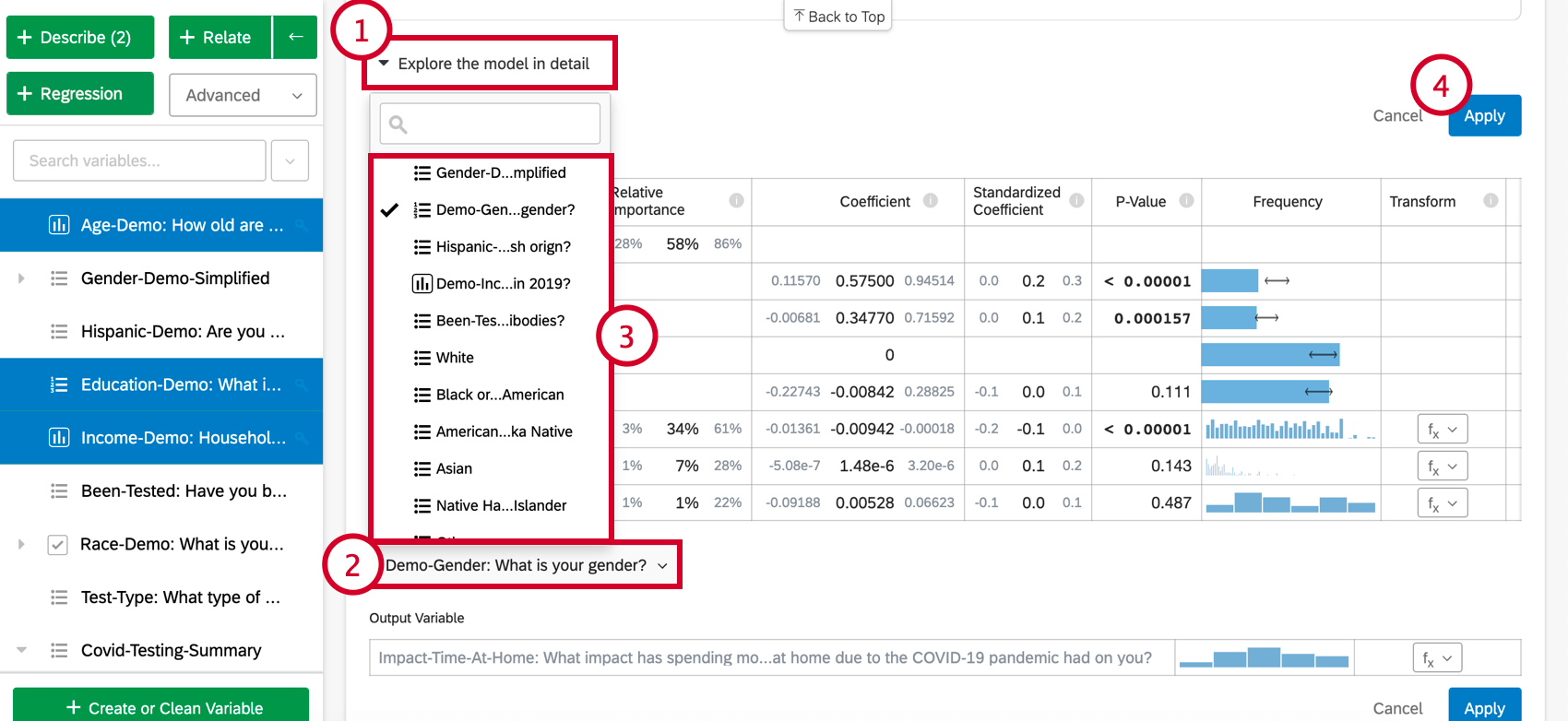
1. モデルを詳しく見る」をクリックする。
2. カードの下にあるAdd variables to your modelを選択します。これは、回帰にまだ使われていない変数のリストを表示します。
3. このリストから変数を選ぶ。
4. 適用(Apply)をクリックして、新しい変数を含めて分析を再実行する。

回帰から変数を除去するには、目的の変数にカーソルを合わせて、表の右端の青いXをクリックします。追加または削除する変数を選択したら、必ず “適用 “を選択して新しいモデルを実行してください。

変数のインプット

回帰は、すべての入力変数がデータを持っている行だけを考慮する。しかし、アンケート調査のデータ収集にはしばしば欠測があり、回帰分析やデータ・モデリングに悪影響を及ぼすことがある。欠損データのない行だけを回帰に含めると、サンプルがデータ集合全体を代表していないため、分析結果にバイアスがかかることがあります。

インピュテーションにより、Stats iqは自動的に欠損データを推定値で埋めます。欠損データが埋められると、より多くの元のデータを回帰分析に含めることができ、その結果、目的の結果変数の変動をよりよく説明できるバイアスの少ない回帰モデルが得られます。

インピュテーションは自動的に行われるので、欠損値のあるデータセットで回帰分析を実行すると、計算が行われる前にデータセットがインピュテーションされます。

変数のインピュテーション前後のデータセットの例を見るには、ここをクリックしてください。

インプット前：
この回帰では、”データ使用量 “を結果変数とし、”年齢”、”インターネットサービス”、”スクリーンタイムの分数 “を入力変数とする。

行ID	データ利用	年齢	インターネットサービス	スクリーンタイム（タイミング）
1日	75	39	サテライト	503
2	19	41	光ファイバー	52
3	87			434
4日	54	23	サテライト
5	14			101
6	75		サテライト
7	81	57	DSL	329

注意欠損値を埋めずに回帰を実行した場合、行 1, 2, 7 だけが含まれます。

インピュテーションの後

行ID	データ利用	年齢	インターネットサービス	スクリーンタイム（タイミング）
1日	75	39	サテライト	503
2	19	41	光ファイバー	52
3	87	50.9	不明	434
4日	54	23	サテライト	359.0
5	14	50.9	不明	101
6	75	50.9	サテライト	359.0
7	81	57	DSL	329

Qtip:“Internet Service “はカテゴリー変数であり、数値変数ではないので、欠損値は “MISSING “として埋められる。

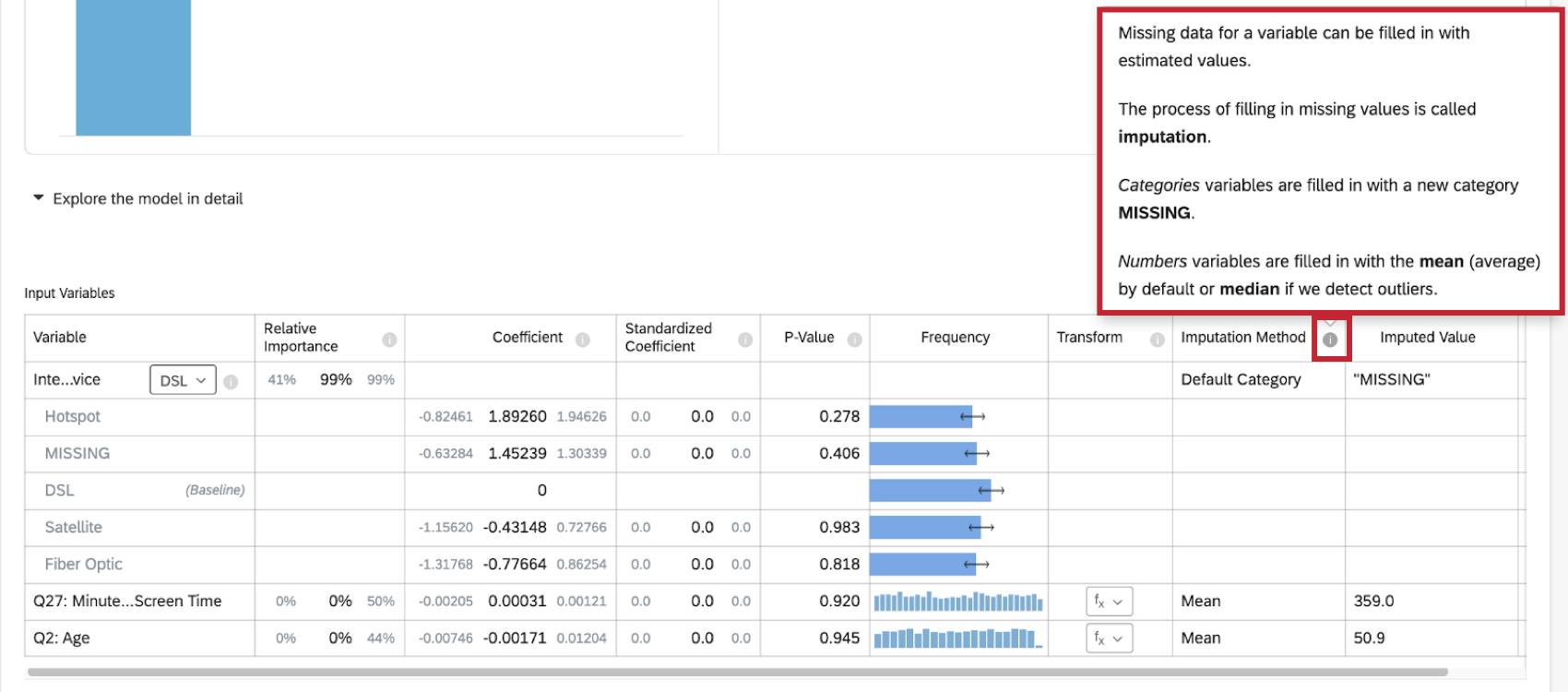
インピュテーション法

Stats iqは現在、以下のインピュテーション法を使用しています：

• デフォルトのカテゴリー：Stats iQは、欠測データを埋めるために新しい「MISSING」カテゴリー値を作成します。この方法は、カテゴリー変数に使用される。
• 平均：Stats iQが数値変数の配信に外れ値がないことを検出した場合、その変数の欠損データは平均値で埋められます。この方法は数値変数に使用される。
• 中央値：Stats iQが数値変数の配信において外れ値を検出した場合、その変数の欠損データは中央値で埋められます。この方法は数値変数に使用される。

インプット指標

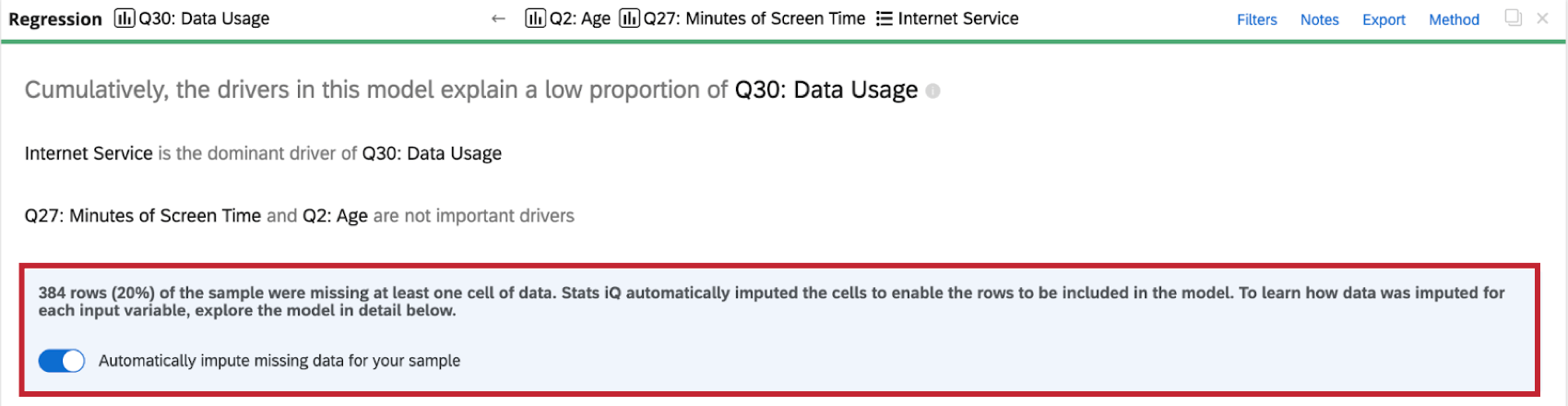
データ集合で回帰分析を実行すると、回帰カードの上部にインピュテーションのインジケータが表示されます。

インピュテーションの詳細については、インピュテーション法の次へ の情報記号（i）をクリックしてください。

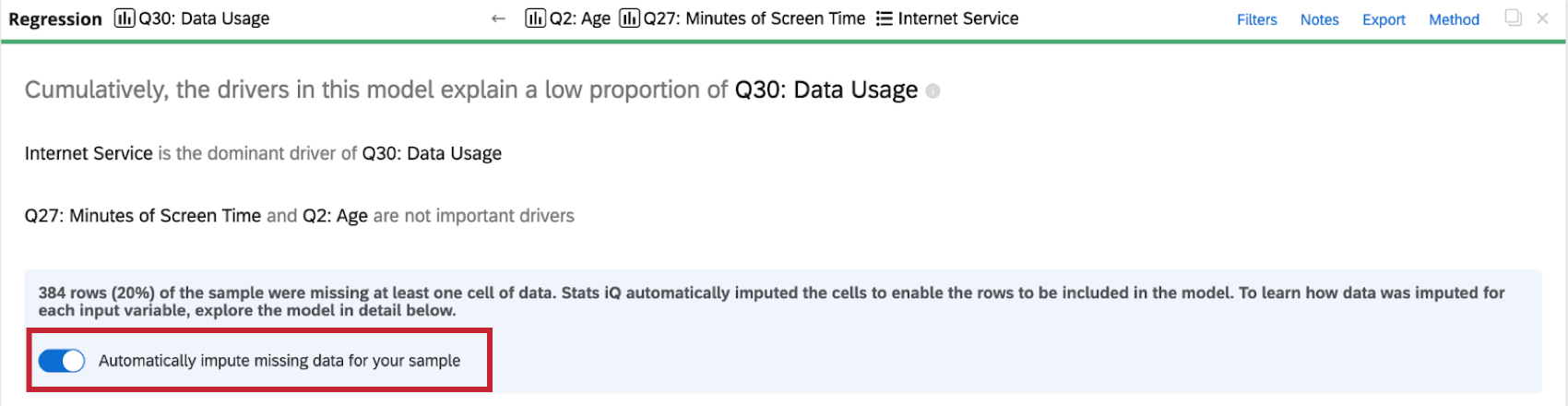
インプットを無効にする

Stats iQは、すべての回帰カードに自動的にインピュテーションを適用します。自動インピュテーションを無効にするには，回帰カードの上部にあるサンプルの欠損データを自動的にインピュートするをクリックする．

インプット警告

• あまりに多くのデータがインプットされると、回帰モデルにバイアスがかかり、信頼できなくなります。データセットの50%以上が入力されると、Stats iqは回帰結果から結論を出すことについて警告します。
  
• 数値入力変数のいずれかに外れ値が検出された場合、Stats iqは平均値の代わりに中央値を使用して変数をインプットします。このシナリオでは、Stats iQはモデルを詳しく探索すると警告を発します。
  

変数の変換

Stats iQで回帰分析を実行すると、モデルを改善する必要があることがわかります。モデルを改善する最も一般的な方法は、1つまたは複数の変数を変換することであり、通常は「log」またはその他の関数変換を使用する。

変数の変換によって、変数の分布の形が変わります。一般に、回帰モデルは、より対称的なベル型の配信でよりよく機能する。このような配信ができるようになるまで、さまざまな種類の変換を試してみてください。

変数を変換する：

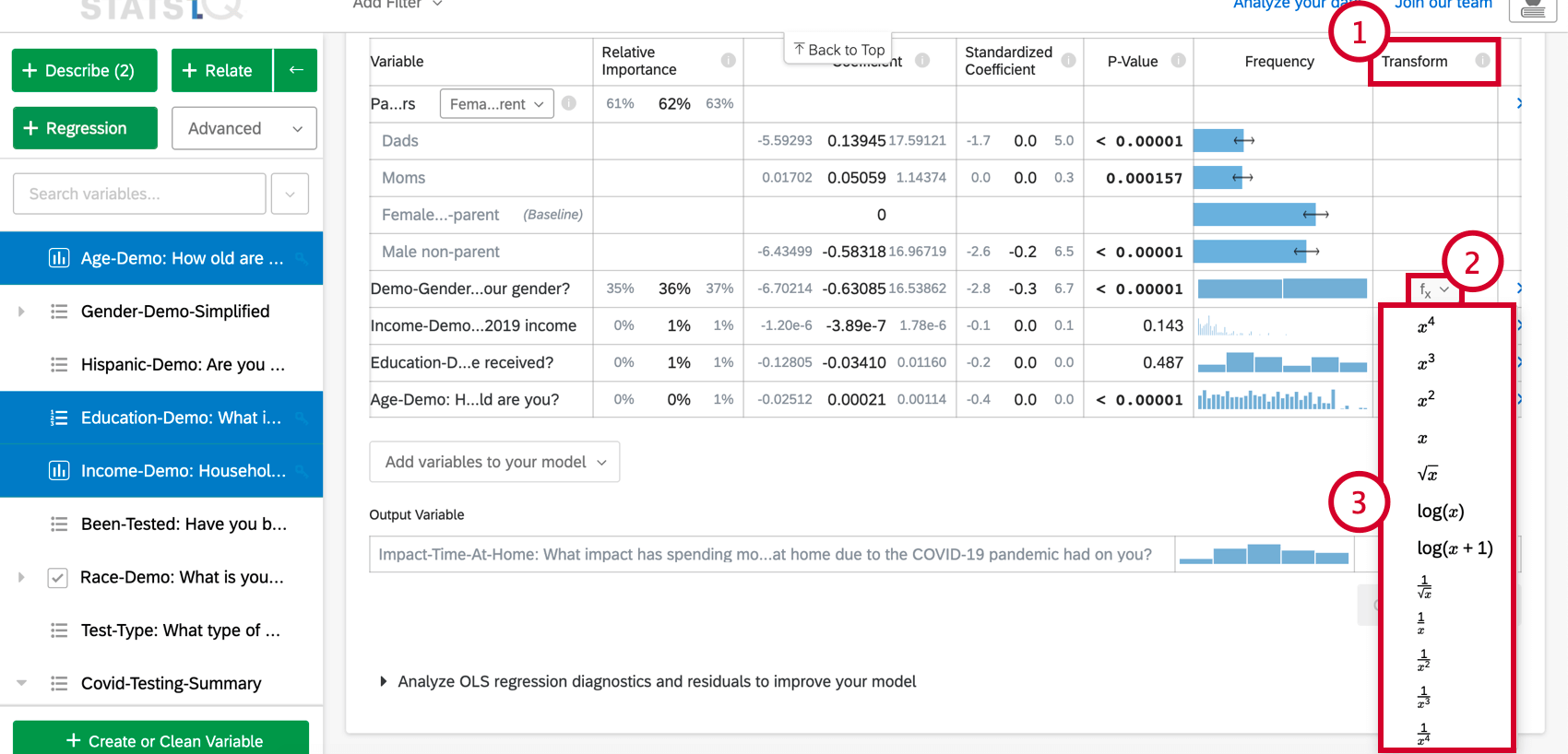
1. モデルを詳しく見る(Explore the model in detail)オプションで、変形(Transform) 列までスクロールする。
2. 変換したい変数の関数(f(x))ボタンをクリックする。
3. リストから適用したい関数を選択すると、Stats iQが新しい変換変数を使用してカードを再計算します。

Stats iQでは以下の変換が可能です：

最も一般的な変換はlog(x)である。小さい値が多く、大きい値が少ない「べき乗」配信（母集団のサイズのような）を、ほとんどの値が真ん中にクラスタ化された釣鐘型の「正規分布」（身長のような）に変換します。

xがゼロのときはlog(x)は計算できないので、変換される変数にゼロの値がある場合はlog(x+1)を使う。

変数を変換するタイミングの詳細については、線形回帰を改善するための残差プロットの解釈を

参照してください。

Stats iQで利用可能なその他の線形回帰テクニック

相対重要度と最小2乗法の組み合わせは，線形回帰のデフォルト出力である．しかし、他の選択肢もある。

M推定、最小2乗法、リッジ回帰にアクセスするには、回帰カードの右上の設定歯車をクリックしてください。回帰手法の 下の回帰手法の名前をクリックすると、回帰カードに使用される回帰手法を変更できる。これは線形回帰でのみ可能である。

• M推定：最小二乗法(OLS)よりも出力変数の外れ値をうまく扱えるように設計されている。
• 最小2乗法最小二乗法（OLS）は、古典的な回帰手法である。ITは外れ値やその他の仮定違反に敏感なので、M推定のようなよりロバストな方法を推奨する。デフォルトの相対重要度出力ではOLSが使用されているので、相対重要度出力にまだ適応されていない機能（結果の予測と交互作用項の追加）に興味がある場合にのみ、このオプションを選択してください。
• リッジ回帰：リッジ回帰は，標準のOLS回帰に似た手法であるが，アルファ調整パラメータを持つ．このアルファ・パラメータは、分散が大きく、多重共線性に悩まされるデータに対処するのに役立つ。適切に調整された場合，リッジ回帰は，バイアスと分散の間のよりよい妥協により，一般にOLSよりもよい予測をもたらす．Stats iQでは、リッジ回帰を使用する際にアルファ・パラメータを選択することができます。

M推定、普通の最小2乗法、またはリッジ回帰を選択すると、出力を見ることができます。出力は、回帰法のセクションの下に表示されます。

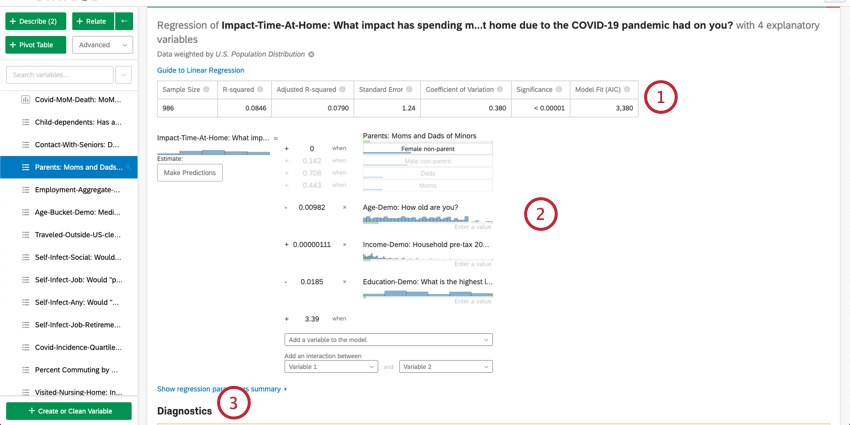
1. 数値要約： カードの一番上には回帰分析の要約がある。これには、サンプルサイズ、欠損症例、手法、R2乗値、標準誤差、変動係数、モデル適合が含まれます。
2. 係数の詳細：回帰の主な結果（数式）は、要約の下にある。出力/キー変数は式の左側にある。入力変数は右側にある。変数の上にカーソルを置くと、その変数が出力変数にどのように寄与するかをわかりやすく説明するツールチップが表示される。ここでは、出力変数の値を推定するための数式に値を入力することもできます。詳細については、出力変数の値の推定に関する以下のセクションを参照のこと。
3. 診断と残差Stats iQは、モデルの精度と検証の評価に役立つ診断を提供します。詳細を見るには、「線形回帰を改善するための残差プロットの解釈」または「ロジスティック回帰でのコンフュージョン・マトリックスと精度-再現性のトレードオフ」をご覧ください。

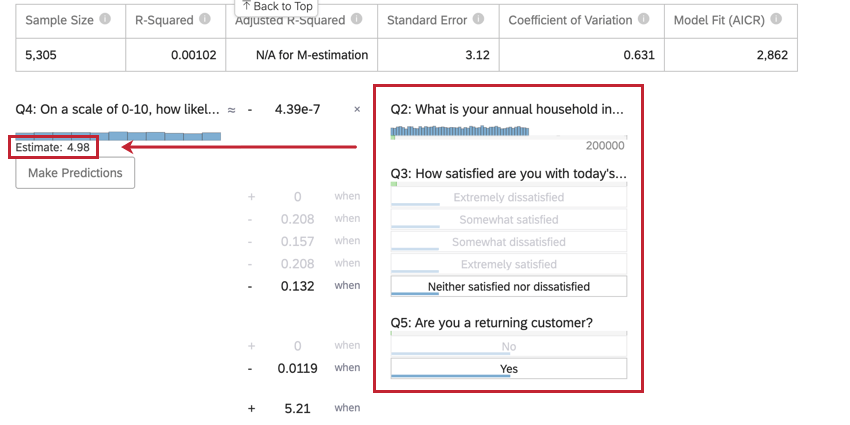
出力変数の値の推定

回帰を実行すると、選択した入力値に基づいて出力変数の値を推定するために、係数の詳細セクションの数式を使用することができます。方程式の右側には、入力変数が表示されます。各入力変数に値を設定することができます。方程式の左側が出力変数である。入力変数の値を入力すると、式は回帰モデルに基づいて出力変数の推定値を計算します。

1. この入力変数は変数タイプである。カテゴリー変数に値を入力するには、オプションのリストから希望の値をクリックする。
2. これらの入力変数は変数タイプである。変数タイプの数値を入力するには、「Enter a value」をクリックして数値を入力する。
3. この変数は回帰式の出力変数である。入力変数の値を選択すると、出力変数の推定値が、推定と書かれた次へ表示されます。

例以下の例では、いくつかの入力変数に基づいて顧客のNpsを予測しようとしています。入力変数の値を選択した後、4.98の推定NPSスコアを見ることができる。

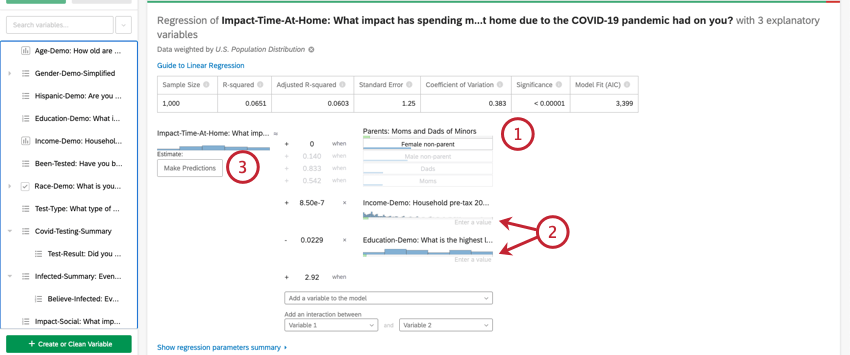
結果の予測

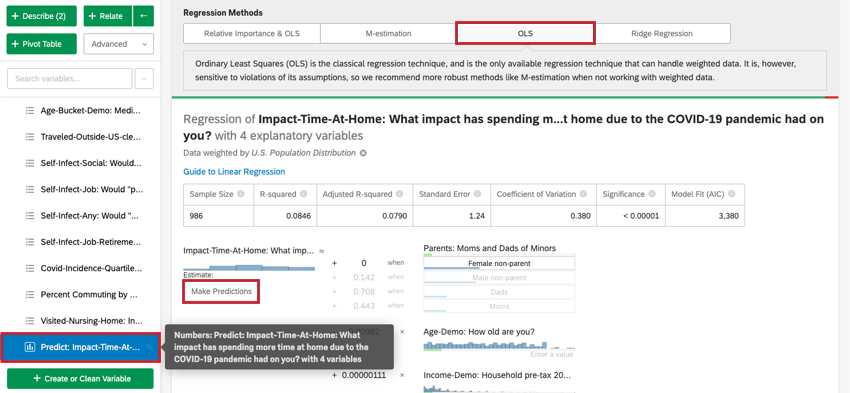
通常、Stats iqでは、入力変数と出力変数の関係を理解するために回帰分析を使用します。しかし、いったん回帰モデルが作成されると、入力の値を持つデータ行の出力値を予測するためにも使用できます。

相互作用の用語とその他の高度な懸念事項

相互作用項の追加

回帰モデルを改善するために、既存の入力変数に加えて交互作用項を追加したい場合があります。交互作用項は、入力変数の1つの値が、別の入力変数が出力変数に与える影響を変えると思われる場合に追加します。

例えば、ホテル滞在中に子供がいる場合、若い人の方が年配者よりも満足度が高いかもしれないが、子供がいない場合、若い人の満足度は低い。つまり、”子供の存在 “と “年齢 “の間に相互作用があるということだ。

カードの入力変数のリストの一番下にあるAdd an interaction betweenで2つの変数を選択すると、回帰に交互作用項が追加されます。この機能は、最小2乗法、M推定、リッジ回帰でのみ利用できる。

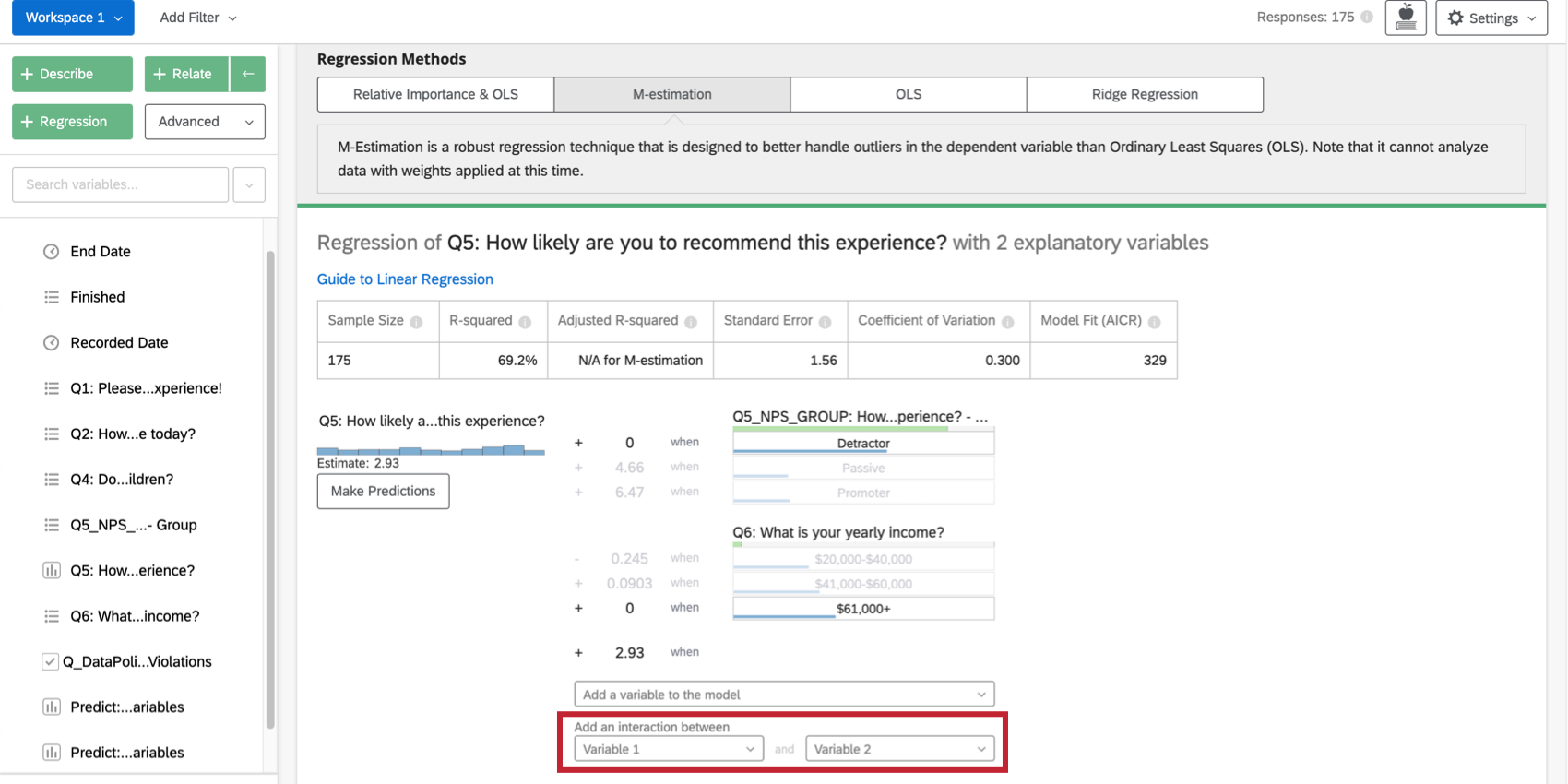
相対重要度分析のカテゴリ変数では、この2つを組み合わせた新しい変数を作成することで、同じ効果を得ることができます。例えば、変数Color（赤と緑の グループ）とSize（大と小のグループ）を組み合わせて、ColorSize （BigRed、BigGreen、SmallRed、SmallGreenのグループ）という変数を作ることができます。

多重共線性

多重共線性は，2つ以上の入力変数が互いに高い相関を持つときに回帰の文脈で発生する．

2つの変数が高度に相関している場合，一般に回帰の数学は，一方の変数にできるだけ値を入れ，もう一方の変数には値を入れない．これは、その変数の係数が大きくなることで現れる。しかし、モデルが少しでも変更されると（たとえばフィルタを追加するなど）、値の大部分が置かれていた変数が変更される可能性がある。これは、わずかな変化でも回帰モデルに劇的な影響を与える可能性があることを意味する。

相対的重要度分析はこの問題を処理するので、心配する必要はない。他の方法を使用することを好み、モデルにこの問題がある場合、多重共線性（”分散インフレーション係数 “で測定）の存在は、警告をトリガーし、例えば、変数を削除するか、平均化することによって変数を結合することを提案します。

警告メッセージ

Stats iqは、回帰結果に潜在的な問題がある場合に警告を発します。これには以下のような状況が含まれる：

• 回帰の入力変数は統計的に有意ではない。
• あなたの変換は回帰からデータを削除した。
• 2つ以上の変数が互いに高い相関を持ち、結果を不安定にしている（多重共線性）。
• 残差はモデルの改良を示唆するパターンを持っている。
• 値が1つしかない変数は自動的に削除された。
• 回帰の入力変数の数に対して、サンプルサイズが小さすぎる。
• 回答オプションが多すぎるカテゴリー変数が追加されました。

FAQ