コレスポンデンス 分析(BX)
コレスポンデンス 分析について
コレスポンデンス分析は、分割表で指定されたデータに基づいて、2 つの変数グループ間の相対関係を明確にします。ブランドイメージには、以下の 2 つのグループがあります。
- ブランド
- これらのブランドに適用される属性
たとえば、ある会社が消費者が異なる飲料ブランドと関連している属性について知りたいとします。コレスポンデンス分析は、ブランド間の類似点や、さまざまな属性との関係におけるブランドの強みを測定するのに役立ちます。相対的な関係を理解することで、ブランドオーナーは、以前のアクションがさまざまなブランド関連の属性にどのような影響を与えたかを特定し、次に取るべきステップを決定できます。
コレスポンデンス分析が、ブランド認識において重要な理由はいくつかあります。ブランドと属性の間の相対的な関係を調べようとすると、ブランドのサイズによって誤解を招く可能性がありますが、コレスポンデンス分析によってこれを解決できます。また、コレスポンデンス分析では、他の多くのグラフでは提供されない(原点との近さおよび距離に基づいた)ブランド属性関係を直感的かつ簡単に把握できます。
このページでは、さまざまな (架空の) 炭酸飲料ブランドの事例にコレスポンデンス分析を適用する方法を紹介します。
まず、入力データ形式、分割表から始めましょう。
分割表
分割表は行と列に変数グループを持つ2次元の表です。上記で説明したように、変数グループが「ブランド」と「その関連属性」であった場合、調査を実施し、異なるブランドと指定された属性に関連付けられたさまざまな回答数を得ることになります。表の各セルは、その属性とそのブランドに関連付けられた回答数を表しています。この「関連付け」は「___ の属性だと思われるブランドを以下のリストから選択してください」というようなアンケート質問で表現されます。
ここでは「ブランド」(行)と「属性」(列)の 2 つ変数グループがあります。右下隅のセルは、「Brawndo」ブランドで「経済的」属性の回答数を表します。
| おいしい | 美しい | 経済的 | |
| Butterbeer | 5 | 7 | 2 |
| Squishee | 18 | 46 | 20 |
| Slurm | 19 | 29 | 39 |
| Fizzy Lifting Drink | 12 | 40 | 49 |
| Brawndo | 3 | 7 | 16 |
残差(R)
コレスポンデンス分析では、各セルの残差を調べます。残差は、観測データと期待データの差異を定量化します。行カテゴリーと列カテゴリー(ここではブランドと属性)の間に関係性がないと仮定します。正の残差は、そのブランド属性のペア件数が予想よりもはるかに多いこと、つまり関係が強いことを示しています。同様に、負の残差は予想よりも低い値、つまり関係が弱いことを示しています。これらの残差の計算方法を見ていきましょう。
残差(R)はR = P – Eとなります。ここでは、Pは各セルで観測された比率、Eは各セルで期待される比率です。これらの観測比率と期待比率を詳しく見てみましょう。
観測比率 (P)
観測比率(P)は、あるセルの値を表全体の値の合計で割ったものです。したがって、上の分割表の場合、合計値は 5 + 7 + 2 + 18 … + 16 = 312 になります。各セル値を合計値で割ると、以下のような観測比率 (P) ができます。
たとえば、右下のセルでは、初期のセル値16を312で割るので、0.051となります。これは、収集されたデータに基づいて「Brawndo」と「経済的」のペアが表全体の中で占める割合を示しています。
| おいしい | 美しい | 経済的 | |
| Butterbeer | 0.016 | 0.022 | 0.006 |
| Squishee | 0.058 | 0.147 | 0.064 |
| Slurm | 0.061 | 0.093 | 0.125 |
| Fizzy Lifting Drink | 0.038 | 0.128 | 0.157 |
| Brawndo | 0.01 | 0.022 | 0.051 |
行の質量と列の質量
観測比率から簡単に計算でき、後々よく使用されるのは、比率表の行と列の合計です。これらは行の質量と列の質量として知られています。行の質量、または列の質量とは、その行や列にある値の比率のことです。上の表を見ると「Butterbeer」の行の質量は、0.016 + 0.022 + 0.006 = 0.044となります。
同様の計算を行うと以下のようになります.
| おいしい | 美しい | 経済的 | 行の質量 | |
| Butterbeer | 0.016 | 0.022 | 0.006 | 0.044 |
| Squishee | 0.058 | 0.147 | 0.064 | 0.269 |
| Slurm | 0.061 | 0.093 | 0.125 | 0.279 |
| Fizzy Lifting Drink | 0.038 | 0.128 | 0.157 | 0.324 |
| Brawndo | 0.01 | 0.022 | 0.051 | 0.083 |
| 列の質量 | 0.182 | 0.413 | 0.404 |
期待比率(E)
期待比率(E)は、各セルの比率として期待される値です。行と列の間に関連性がないと仮定します。セルの期待値は、そのセルの行の質量と列の質量の積です。
左上のセルでは「Butterbeer」の行の質量と「おいしい」の列の質量の積、0.044 x 0.182 = 0.008 が表示されています。
| おいしい | 美しい | 経済的 | |
| Butterbeer | 0.008 | 0.019 | 0.018 |
| Squishee | 0.049 | 0.111 | 0.109 |
| Slurm | 0.051 | 0.115 | 0.113 |
| Fizzy Lifting Drink | 0.059 | 0.134 | 0.131 |
| Brawndo | 0.015 | 0.034 | 0.034 |
これで残差(R)表(R = P – E)を計算できるようになりました。残差は観測データ比率と期待データ比率の差を定量化します。ここでは行と列に関連性がないと仮定します。
最も小さい負の値である「Squishee」と「経済的」の-0.045を見てみましょう。「Squishee」と「経済的」は負の関係があると解釈できます。つまり「Squishee」は「経済的」なブランドとみなされる可能性が、他の飲料ブランドよりもはるかに低いということです。
| おいしい | 美しい | 経済的 | |
| Butterbeer | 0.008 | 0.004 | -0.012 |
| Squishee | 0.009 | 0.036 | -0.045 |
| Slurm | 0.01 | -0.022 | 0.012 |
| Fizzy Lifting Drink | -0.021 | -0.006 | 0.026 |
| Brawndo | -0.006 | -0.012 | 0.018 |
指標化残差(I)
ただ残差を読み取るだけでは問題があります。
上記の残差計算表の一番上の行を見ると、これらの数値はすべてほぼゼロであることがわかります。だからと言って、この結果から「Butterbeerとこれらの属性との関係性はない」という極端な結論を導くべきではありません。なぜなら、その仮定は間違っているからです。観測比率(P)と期待比率(E)が小さいのは、行の質量が示すように、Butterbeerの割合がサンプルの4.4%しかないためです。
これは、残差を調べる場合に大きな問題となります。行や列の実際のレコード数を無視しているため、結果が質量の大きい行や列に偏ってしまうためです。これは、残差を期待比率(E)で割ることで修正できます。これにより、指標化残差の表(I, I = R / E)
を得られます。
| おいしい | 美しい | 経済的 | |
| Butterbeer | 0.95 | 0.21 | -0.65 |
| Squishee | 0.17 | 0.32 | -0.41 |
| Slurm | 0.2 | -0.19 | 0.11 |
| Fizzy Lifting Drink | -0.35 | -0.04 | 0.2 |
| Brawndo | -0.37 | -0.35 | 0.52 |
指標化残差の解釈は簡単です。値が表より外れるほど、観測比率が期待比率に対して大きくなることを示しています。
たとえば、左上の値を見てみると、Butterbeerは、これらのブランドと属性の間に関係がない場合に期待されるものよりも、「おいしい」と見なされる確率が95%高くなっています。一方、右上の値を見ると、Butterbeerが「経済的」と見なされる確率が65%低くなっています。ここでも、ブランドと属性の間に関係がない場合を考慮しています。
| おいしい | 美しい | 経済的 | |
| Butterbeer | 0.95 | 0.21 | -0.65 |
| Squishee | 0.17 | 0.32 | -0.41 |
| Slurm | 0.2 | -0.19 | 0.11 |
| Fizzy Lifting Drink | -0.35 | -0.04 | 0.2 |
| Brawndo | -0.37 | -0.35 | 0.52 |
指標化残差(I)、期待比率(E)、観測比率(P)、行の質量および列の質量から、表のコレスポンデンス分析値を計算してみましょう。
コレスポンデンス分析の座標を計算する
特異値分解(SVD)
最初に、特異値分解(SVD)を計算します。SVDを使用して分散を計算し、行(ブランド)や列(属性)をプロットするための値を求めます。
標準化残差(Z)でSVDを計算します。Z = I * sqrt(E) となり、I は指標化残差、E は期待比率です。Eを乗算してSVDの重み付けをします。これにより、セルの期待値が高いほどより高い重みが、低いほど低い重みが付けられます。期待値はサンプルサイズと関係性がある場合が多く、サンプリング誤差が大きくなるような、表の 「小さい」セルの重みは低くなるということです。従って、分割表を用いたコレスポンデンス分析は、サンプリング誤差によって発生する外れ値の影響を受けにくくなっています。
SVDの話に戻りましょう。SVD = svd(Z)です。特異値分解は3つの出力を生成します。
1つ目は、特異値を含むベクトルdです。
| 第1次元 | 第2次元 | 第3次元 |
| 2.65E-01 | 1.14E-01 | 4.21E-17 |
2つ目は、左の特異ベクトル(ブランド)を含む行列u です。
| 第1次元 | 第2次元 | 第3次元 | |
| Butterbeer | -0.439 | -0.424 | -0.084 |
| Squishee | -0.652 | 0.355 | -0.626 |
| Slurm | 0.16 | -0.0672 | -0.424 |
| Fizzy Lifting Drink | 0.371 | 0.488 | -0.274 |
| Brawndo | 0.469 | -0.06 | -0.588 |
3つ目は、右の特異ベクトル(属性)を含む行列vです。
| 第1次元 | 第2次元 | 第3次元 | |
| おいしい | -0.41 | -0.81 | -0.427 |
| 美しい | -0.489 | >0.59 | -0.643 |
| 経済的 | 0.77 | -0.055 | -0.635 |
左の特異ベクトルは表の行カテゴリーに、右の特異ベクトルは列カテゴリーに対応します。分散を計算するための各特異値と、位置をプロットするための対応するベクトル(uとvの行列)は、それぞれ1つの次元に対応しています。コレスポンデンス分析グラフで行と列のカテゴリーのプロットに使用される座標は、最初の2つの次元から求められます。
次元で表現される分散
特異値の二乗は固有値(d^2)と呼ばれます。この例の固有値は、0.0704、0.0129、0.0000です。各固有値を総和の比率として表すことで、コレスポンデンス分析の各次元で捉えられた分散量がわかります。各次元の特異値をもとに、第1次元で表現される分散は84.5%、第2次元では15.5%となります(第3次元では分散は0%です)。
標準コレスポンデンス分析
これで、左の特異ベクトルと右の特異ベクトルから算出した標準座標を使用して、コレスポンデンス分析の基本形を計算するためのリソースが準備できました。前の手順で、SVDを実行する前に指標化残差に重み付けをしました。指標化残差を表す座標を得るには、SVDの出力を重みを付けていない状態にする必要があります。左の特異ベクトルの各行を行の質量の平方根で徐算し、右の特異ベクトルの各列の列の質量の平方根で徐算します。これでプロット用の行と列の標準座標が得られます。
ブランドの標準座標:
| 第1次元 | 第2次元 | 第3次元 | |
| Butterbeer | -2.07 | -2 | -0.4 |
| Squishee | -1.27 | 0.68 | -1.21 |
| Slurm | 0.3 | -1.27 | -0.8 |
| Fizzy Lifting Drink | 0.65 | 0.86 | -0.48 |
| Brawndo | 1.62 | -0.21 | -2.04 |
属性の標準座標:
| 第1次元 | 第2次元 | 第3次元 | |
| おいしい | -0.96 | -1.89 | -1 |
| 美しい | -0.76 | 0.92 | >-1 |
| 経済的 | 1.21 | -0.09 | -1 |
分散が最も大きい2つの次元をプロットに使用します。第1次元をX軸に、第2次元をY軸に配置し、標準コレスポンデンス分析グラフを生成します。

標準コレスポンデンス分析に必要な計算の基礎ができました。次のセクションでは、コレスポンデンス分析の各形式の長所と短所、およびブランド認識の分析に最も適した形式を探ります。
コレスポンデンス分析の種類
行/列優先コレスポンデンス分析
標準コレスポンデンス分析は計算が簡単で、そこから信頼性の高い、有意義な結果を導き出すことができます。しかし、標準コレスポンデンス分析は私たちのニーズには合っていません。行と列の座標間の距離が誇張されており、行と列のカテゴリー間の関係が明確に解釈できないからです。行(ブランド)の座標間の関係を解釈し、行と列のカテゴリー間の関係を解釈するために必要なのは、行優先正規化です(または、ブランドが列にある場合は、列優先正規化になります)。
行優先正規化を行うには、列(属性)値には上記で計算された標準座標を利用しますが、行(ブランド)値の場合は主座標を計算する必要があります。主座標の計算は簡単で、標準座標を取得し、対応する特異値(d)で乗算するだけです。行についても、行の標準座標を特異値(d)で乗算するだけでよく、以下の表のようになります。列優先正規化の場合は、行ではなく列を特異値(d)で乗算します。
| 第1次元 | 第2次元 | 第3次元 | |
| Butterbeer | -0.55 | -0.23 | 0 |
| Squishee | -0.33 | 0.08 | 0 |
| Slurm | 0.08 | -0.14 | 0 |
| Fizzy Lifting Drink | 0.17 | 0.1 | 0 |
| Brawndo | 0.43 | -0.02 | 0 |
行(ブランド)の主座標を代入すると以下のようになります。

縮尺に特異値を使用したため、行の主座標は元の表の行プロファイル間の距離を表しています。このため、コレスポンデンス分析グラフにおける行座標間の関係を、互いの近接度で解釈できます。
列の座標間の距離は、標準座標に基づいているため、まだ実際よりも大きく表示されています。また、2つのカテゴリー(行/列)のうち一方だけを特異値を使用して変換することで、行と列のカテゴリー間の関係を解釈できるようになりました。たとえば、行の値と列の値が「Butterbeer」(行)と「おいしい」(列)である場合、それらが原点から遠いほど、他のマップ上の点との関連性が強いことを示しています。また、2つの点(「Butterbeer」と「おいしい」)の間の角度が小さいほど、2点間の相関が高くなります。

原点までの距離と2点間の角度の組み合わせは、内積と等しくなります。行の値と列の値の内積は、両者の関連の強さを表します。実際、第1次元と第2次元でデータのすべての分散を説明する場合(合計で100%になる場合)、内積は2つのカテゴリーの指標化残差と直接等しくなります。ここでは、内積は2点の原点からの距離にそれらの間の角度のコサインを乗算したものになります。つまり、0.59 * 2.12 * cos(41°) = 0.94となります。丸め誤差を考慮に入れると、これは指標化残差値の0.95と同じです。従って、90度より小さい角度は正の指標化残差を表し、正の関連性があることを示します。一方、90度より大きい角度は負の指標化残差、つまり負の関連性を表します。
スケール行優先コレスポンデンス分析
上の行優先正規化グラフを見てみると、列(特性)の点は広範囲に散らばっており、行(ブランド)の点は原点の周りに集まっているのがわかります。グラフを見ただけで分析することが非常に難しくなり、直感的ではなく、行のカテゴリーがすべて重なっている場合には読み取りできなくなることもあります。幸い、内積(原点からの距離と2点間の角度)を利用して行と列の点の関係を解析する機能を活用しながら、列を取り込んでグラフを調整する簡単な方法があります。これをスケール行優先正規化と言います。
スケール行優先正規化は、行優先正規化を行い、列の座標を行の座標のx軸と同じ方法で調整します。つまり、列の座標は特異値(d)の最初の値で調整されます。行の値は行優先正規化と同じままですが、今度は列の座標が定数係数でスケールダウンされます。
| 第1次元 | 第2次元 | 第3次元 | |
| おいしい | -0.2544 | -0.501 | -0.265 |
| 美しい | -0.201 | 0.2438 | -0.265 |
| 経済的 | 0.321 | -0.02 | -0.265 |
これで列の座標が行の座標と同じスケールに調整され、適合するので、トレンド分析が非常に簡単になります。すべての列座標を同じ定数係数でスケールダウンしたため、マップ上の列座標の散布は小さくなりましたが、それらの相対性には変更を加えていません。つまり、関連性の強さを測るには引き続き内積を利用します。唯一変わったのは、第1次元と第2次元がデータの全ての分散を網羅すると、指標化残差が2つのカテゴリーの内積に等しくなるのではなく、2つのカテゴリーのスケール内積に等しくなることです。これは、最初の特異値(d)の定数値で調整した内積のことです。グラフの解釈は、行優先正規化と同じです。

優先コレスポンデンス分析
最後に説明するコレスポンデンス分析の形式は、優先コレスポンデンス分析です。対称マップ、フレンチスケーリング、またはカノニカルコレスポンデンス分析とも呼ばれています。行/列優先コレスポンデンス分析のように標準行または標準列だけを特異値(d)で乗算するのではなく、両方を特異値で乗算します。したがって、標準列値を特異値で乗算すると次のようになります。
| 第1次元 | 第2次元 | 第3次元 | |
| おいしい | -0.2544 | -0.215 | 0 |
| 美しい | -0.201 | 0.105 | 0日 |
| 経済的 | 0.321 | -0.01 | 0 |
これを行優先分析で計算された行値と合わせると、次のようになります

。カノニカルコレスポンデンス分析は、行と列の座標の両方を特異値で調整します。これは(近接性に基づく)行優先コレスポンデンス分析と同様に、行座標間の関係を解釈できること、および列優先コレスポンデンス分析と同様に、列座標間の関係を解釈できること、つまり、ブランド間の関係および属性間の関係が分析できるということです。行/列優先分析により、マップの中心にある行/列のクラスタリングもなくなります。しかし、カノニカルコレスポンデンス分析では、ブランド認識に非常に役立つ、ブランドと属性の間の関係を解釈する方法も失われてしまいます。
並列比較
標準コレスポンデンス分析
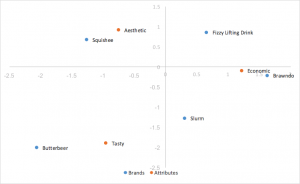
コレスポンデンス分析の中で最も計算しやすい形式で、SVDの左右の特異ベクトルを行の質量と列の質量で除算します。行と列の座標間の距離が大きく表示され、行と列のカテゴリー間の関係の解釈は直感的ではありません。
行優先正規化コレスポンデンス分析
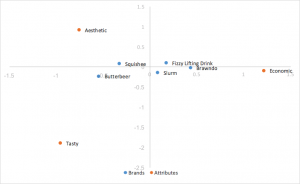
上述の標準座標を使用しますが、行座標を特異値で乗算して正規化します。行(ブランド)間の関係性は、互いからの距離に基づいています。まだ列(属性)間の距離が大きく表示されたままです。行と列の間の関係性は、内積によって解釈できます。行(ブランド)は中央に集まる傾向があります。
スケール行優先正規化コレスポンデンス分析
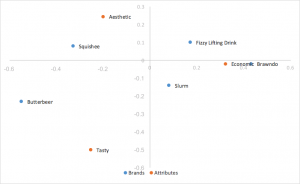
行優先正規化を使用して、最初の特異値の定数で列座標を調整します。行優先正規化と同じ解釈が導き出されますが、内積をスケール内積に置き換えています。中心部に行が集中しないようにする場合便利です。これがクアルトリクスが採用しているコレスポンデンス分析の形式です。
優先正規化コレスポンデンス分析(対称、フレンチマップ、カノニカル)
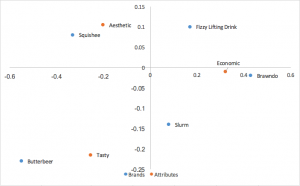
よく使われているもう一つのコレスポンデンス分析の形式で、行と列の両方で優先正規化座標を使用します。行(ブランド)間の関係は、互いの距離によって解釈できます。同じことが列(属性)についても言えます。行と列の間の関係については解釈できません。
まとめ
結論として、コレスポンデンス分析は2つのグループ間、およびグループ内の相対関係を分析するために使われます。今回のケースでは、ブランドと属性です。
コレスポンデンス分析は、指標化残差を使用することで、グループ間の質量が異なるために生じる結果の偏りを取り除きます。コレスポンデンス分析におけるブランド認識については、行優先(またはブランドが列に配置されている場合は列優先)正規化を利用します。これにより、異なるブランド間の関係を、互いの近さによって分析できるようになるとともに、ブランドと属性間の関係を、原点からの距離と原点との角度の組み合わせ(内積)で分析することが可能になります。これには属性間の関係を距離を誇張して表現しまうという欠点が伴います(が、属性間の関係は今回のケースでは重要ではないので、問題にはなりません)。スケール行/列優先正規化を利用することで、コストをかけずにグラフをより簡単に分析できます。X軸とY軸のラベル(第1次元と第2次元)で説明される分散を合計して、マップで捉えられた総分散を確認する必要があります。この数値が低いほど、データには未解明の分散が多く含まれていることになり、プロットが誤解を招きやすくなります。
最後に、コレスポンデンス分析はデータの質量要素を取り除いているため、相対関係しか示さないということに注意してください。従って、このグラフは属性のどのブランドが「最も高い」スコアなのかは示しません。グラフの作成と分析方法を理解すると、コレスポンデンス分析はブランドのサイズ効果を無視し、ブランドとその適用可能な属性、およびブランド内や属性内の関係について、深く解釈しやすいインサイトを提供する強力なツールとなります。