Guida user-friendly alla regressione logistica

Che cos’è la regressione logistica?

La regressione logistica stima una formula matematica che mette in relazione una o più variabili di input con una variabile di uscita.

Ad esempio, si supponga di gestire uno stand di limonata e di essere interessato a quali tipi di clienti tendono a tornare. I tuoi dati includono un inserimento per ogni cliente, il loro primo acquisto e se sono tornati entro il mese successivo per avere più limonata. I dati potrebbero avere il seguente aspetto:

Si ritiene che l'”età del cliente” (una variabile di input o esplicativa) possa influire su “Reso” (una variabile di output o risposta). La regressione logistica potrebbe produrre questo risultato:

All’età di 12 anni (l’età più bassa), la probabilità di ritorno è del 10%.

Per ogni ulteriore anno di età, il “Ritorno” è 1,1 volte di più da “Restituire”.

Questo po’ di conoscenza è utile per due motivi.

In primo luogo, permette di capire una relazione: i clienti più anziani hanno più probabilità di tornare. Queste informazioni potrebbero condurvi a piegare la pubblicità verso i clienti più anziani, poiché saranno più propensi a diventare clienti ricorrenti.

In secondo luogo, e in modo correlato, può anche aiutare a effettuare previsioni specifiche. Se un cliente di 24 anni passeggiasse, potresti stimare che se acquistasse una limonata, c’è una probabilità del 26% che in seguito diventerebbe un cliente di ritorno.

Comprensione della moltiplicazione delle probabilità

Osservate che se dicevamo “Restituito” era “1,5 volte più probabile” in una situazione che in un’altra, stiamo facendo quanto segue:

Le probabilità erano 1:9, scritte anche 1/(1+9) = 10%.

Le “probabilità per” (1) sono moltiplicate per 1,5.

Ora 1,5:9, scritto anche 1.5/(1,5+9) = 14%.

Un altro esempio, questa volta di passare dal 50% di probabilità a qualcosa di 3 volte più probabile:

Le probabilità erano 1:1, scritte anche 1/(1+1) = 50%.

Le “probabilità per” (il lato sinistro 1) sono moltiplicate per 3.

Ora 3:1, scritto anche 3/(3+1) = 75%.

Ora attraverseremo il processo di creazione di questo modello di regressione.

Preparazione alla creazione di un modello di regressione

1. Pensate attraverso la teoria della vostra regressione.

Una volta scelta una variabile di risposta, “Fatturato“ ipotizza come possono esservi correlati vari input. Ad esempio, potresti pensare che una maggiore “Temperatura al primo acquisto” porterà a una maggiore probabilità di “Ritorno”, potresti non essere sicuro di come “Età” influenzerà “Ritorno“, e potresti credere che “Pantaloni” (rispetto ai pantaloncini) sia influenzato da “Temperatura” ma non abbia alcun impatto sul tuo stand di limonata.

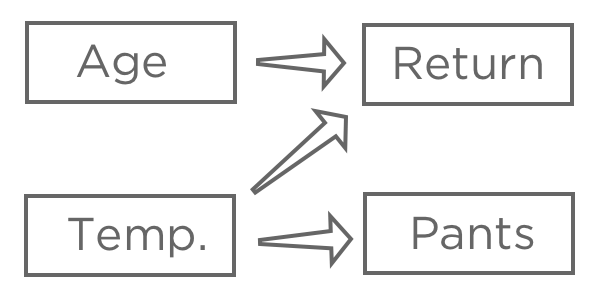
L’obiettivo della regressione è in genere quello di comprendere la relazione tra diversi input e un output, quindi in questo caso probabilmente si deciderebbe di creare un modello che spieghi “Ritorno” con “Temperatura” ed “Età” (detto anche “prevedere il ritorno dalla temperatura e dall’età”, anche se si è più interessati alla spiegazione che alla previsione effettiva).

Probabilmente non includeresti “Pantaloni” nella tua regressione. Potrebbe essere correlato al “Ritorno” perché entrambi sono correlati a “Temperatura”, ma non viene prima di “Ritorno” nella catena causale, quindi l’inclusione confonderebbe il tuo modello.

2. “Descrivere” tutte le variabili che potrebbero essere utili per il modello.

Iniziare descrivendo la variabile di risposta, in questo caso “Ricavi”, e sentirla bene. Eseguire la stessa operazione per le variabili esplicative.

Nota che hanno una forma come questa…

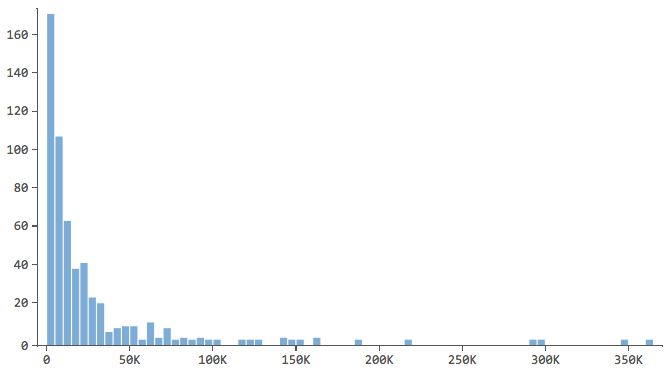
…dove la maggior parte dei dati si trova nei primi bin dell’istogramma. Tali variabili richiederanno in seguito un’attenzione particolare.

3. “Collegare” tutte le possibili variabili esplicative alla variabile di risposta.

Stats iQ ordinerà i risultati in base alla forza della relazione statistica. Dai un’occhiata e ottieni un’idea dei risultati, osservando quali variabili sono correlate al “Fatturato” e in che modo.

4. Iniziare a creare la regressione.

La creazione di un modello di regressione è un processo iterativo. Le tre fasi che seguono saranno eseguite tutte le volte necessarie.

Le tre fasi di costruzione di un modello di regressione

Fase 1: aggiungere o sottrarre una variabile.

Uno alla volta, inizia ad aggiungere nelle variabili che le tue analisi precedenti indicate erano correlate a “Fatturato” (o aggiungi le variabili che hai un motivo teorico da aggiungere). Andare uno alla volta non è strettamente necessario, ma facilita l’identificazione e la risoluzione dei problemi man mano che si procede, aiutandoti a percepire il modello.

Supponiamo di iniziare prevedendo “Fatturato” con “Temperatura”. Si trova un rapporto forte, si valuta il modello e lo si trova soddisfacente (maggiori dettagli in un minuto).

Ritorno <– Temperatura

Quindi si aggiunge “Colore limonata” e ora il modello di regressione ha due termini, entrambi fattori di probabilità statisticamente significativi. Così:

Fatturato <– Temperatura e colore limonata

Quindi si aggiunge “Sesso” e i risultati del modello mostrano ora che “Sesso” è statisticamente significativo nel modello, ma “Colore limonata” non lo è più. In genere si rimuove “Colore limonata” dal modello. Ora abbiamo:

Ricavi <- Temperatura e sesso

Ovvero, se conosci il sesso del cliente, sapere che colore di limonata ha ordinato non ti dà ulteriori informazioni sul fatto che sarà un cliente di ritorno.

Potreste indagare e scoprire che le donne tendono a scegliere la limonata gialla più degli uomini e che le donne hanno più probabilità di ritornare. Così inizialmente sembrava che la scelta del giallo rendesse un cliente più propenso a tornare, ma in realtà, “Lemonade color” è legato solo a “Return” attraverso “Sex“. Quindi quando si include “Sex” nella regressione, “Lemonade color” esce dalla regressione.

Interpretare i risultati della regressione richiede una buona dose di giudizio, e solo perché una variabile è statisticamente significativa, non significa che sia effettivamente causale. Ma aggiungendo e sottraendo con attenzione le variabili, notando come cambia il modello e pensando sempre alla teoria che sta dietro il modello, è possibile mettere in secondo piano relazioni interessanti nei dati.

Fase 2: Valutazione del modello.

Ogni volta che aggiungi o sottrai una variabile, devi valutare l’accuratezza del modello osservandone R quadro (^R2), AICc ed eventuali avvisi di Stats iQ. Ogni volta che si cambia il modello, si confrontano i nuovi grafici R quadro, AICc e diagnostici con quelli vecchi per determinare se il modello è migliorato o meno.

R-quadrato (^R2)

La metrica numerica per la quantificazione dell’accuratezza di previsione del modello è nota come R quadro, che è compresa tra zero e uno. Lo zero indica che il modello non ha un valore predittivo e uno indica che il modello prevede perfettamente tutto.

Ad esempio, i dati rappresentati a sinistra porteranno a un modello molto meno accurato dei dati a destra. Immaginate di cercare di tracciare una linea attraverso la trama a dispersione; potreste separare quasi completamente il blu (“Ritornato”) dal rosso (“Non c’è”) sul lato destro, ma sul lato sinistro sarebbe difficile farlo.

Cioè, il lato destro ha un R quadrato alto; se conosci “Temperatura” ed “Età”, puoi determinare “Restituito” vs. “Non c’era” abbastanza facilmente. Il lato sinistro ha un R quadrato da basso a medio; se conosci “Temperatura” ed “Età”, hai un’ipotesi abbastanza buona se sarà “Restituita” vs. “No”, ma ci saranno molti errori.

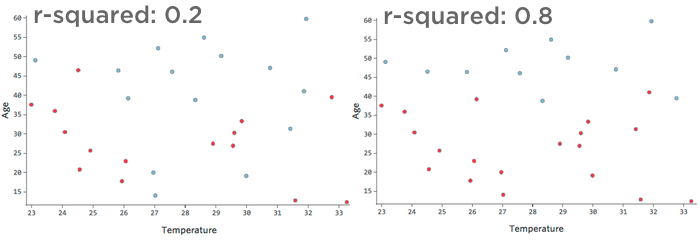
Non esiste una definizione fissa di R quadro “buono”. In alcune impostazioni potrebbe essere interessante vedere qualsiasi effetto, mentre in altre il modello potrebbe essere inutile a meno che non sia altamente accurato.

Ogni volta che si aggiunge una variabile, R quadro salirà, in modo che il raggiungimento dell’R quadro più alto possibile non sia l’obiettivo; piuttosto, si desidera bilanciare l’accuratezza del modello (R quadro) con la sua complessità (in genere, il numero di variabili in esso contenute).

AICc

L’AICc è una metrica che bilancia l’accuratezza con la complessità – una maggiore accuratezza porta a punteggi migliori e maggiore complessità (più variabili) porta a punteggi peggiori. Meglio il modello con l’AICc inferiore.

Si noti che la metrica AICc è utile solo per confrontare gli AICc di modelli che hanno lo stesso numero di righe di dati e la stessa variabile di output.

Avvisi

Di tanto in tanto Stats iQ suggerirà modi per migliorare il tuo modello. Ad esempio, Stats iQ può suggerire di prendere il logaritmo di una variabile (dettagli su cosa significa).

Matrice di confusione e curva Precision-Recall

La matrice di confusione e la curva di precisione/richiamo sono inoltre strumenti utili per comprendere l’accuratezza del modello. Inoltre, se si desidera effettuare previsioni in base al modello, questi strumenti ti aiuteranno a farlo. Non sono strettamente necessari per ottenere una buona comprensione di ciò che il modello ti sta dicendo, quindi li inseriamo in una sezione diversa sulla matrice di confusione e sulla curva di richiamo di precisione

Fase 3: Modificare il modello di conseguenza.

Se la valutazione del modello lo ha giudicato soddisfacente, si è fatto o si può tornare alla Fase 1 e inserire più variabili.

Se la tua valutazione rileva la mancanza del modello, utilizzerai gli avvisi di Stats iQ per risolvere i problemi.

Quando si modifica il modello, notare continuamente le modifiche R quadro, AICR e diagnostica residua e decidere se le modifiche apportate aiutano o danneggiano il modello.

FAQ