Guida user-friendly alla regressione lineare

Che cos’è la regressione?

La regressione stima una formula matematica che mette in relazione una o più variabili di entrata con una variabile di uscita.

Ad esempio, supponiamo di gestire uno stand di limonata e di essere interessato a ciò che genera fatturato. I dati includono “Fatturato” di ogni giorno, “Temperatura” elevata, “Numero di bambini a piedi”, “Numero di adulti a piedi”, “Segnale” utilizzato quel giorno e un “fatturato del concorrente” nelle vicinanze.

Si ritiene che “Temperatura” (una variabile di input o esplicativa) potrebbe influire su “Ricavo” (una variabile di output o di risposta). Quando si utilizza la regressione per analizzare questa relazione, potrebbe risultare questa formula:

Ricavo = 2,71 * temperatura   –   35

Questa formula è utile per due motivi.

Innanzitutto permette di capire una relazione: giorni più caldi portano a maggiori “ricavi”. In particolare, il 2,71 prima di “Temperatura” (detto coefficiente) significa che per ogni grado “Temperatura” sale, in media ci saranno 2,71 dollari in più “Fatturato”. Questa analisi potrebbe portare a decidere di non vendere limonata nei giorni freddi.

In secondo luogo, e in modo correlato, può anche aiutare a effettuare previsioni specifiche. Se la “Temperatura” è 24, si potrebbe stimare che a partire da…

Ricavo = 2,71 * temperatura   –   35
Ricavo = 2,71 * 24   –   35
Fatturato = 30

…avrai circa 30 dollari in “Fatturato”. Potrebbero essere informazioni utili per sapere se sarai in grado di effettuare un pagamento quel giorno, presupponendo che tu sia sicuro che il tuo modello sia accurato.

Ora attraverseremo il processo di creazione di questa equazione di regressione.

Preparazione alla creazione di un modello di regressione

1. Pensate attraverso la teoria della vostra regressione.

Una volta scelta una variabile di risposta, “Fatturato“ ipotizza come possono esservi correlati vari input. Ad esempio, potresti pensare che una “Temperatura” più elevata porterà a un “Fatturato” più alto, potresti non essere sicuro di come i vari segnali influiranno sul “Fatturato” e potresti credere che “Le vendite del concorrente” siano influenzate dalla “Temperatura” ma non abbiano alcun impatto sul vostro stand di limonata.

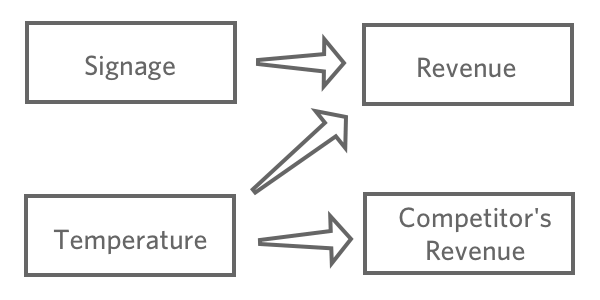
L’obiettivo della regressione è in genere quello di comprendere la relazione tra diversi input e un output, quindi in questo caso probabilmente decideresti di creare un modello che spieghi “Fatturato” con “Temperatura” e “Segnale” (detto anche “previsione dei ricavi da temperatura e segnalamento“, anche se si è più interessati alla spiegazione che alla previsione effettiva).

Probabilmente non si includerebbero “Vendite del concorrente” nella regressione. È probabilmente correlato al “fatturato”, ma non viene prima nella catena causale, quindi l’inclusione confonderebbe il tuo modello.

2. “Descrivi” tutte le variabili che potrebbero essere utili per il modello

Iniziare descrivendo la variabile di risposta, in questo caso “Ricavi”, e sentirla bene. Eseguire la stessa operazione per le variabili esplicative.

Nota che hanno una forma come questa…

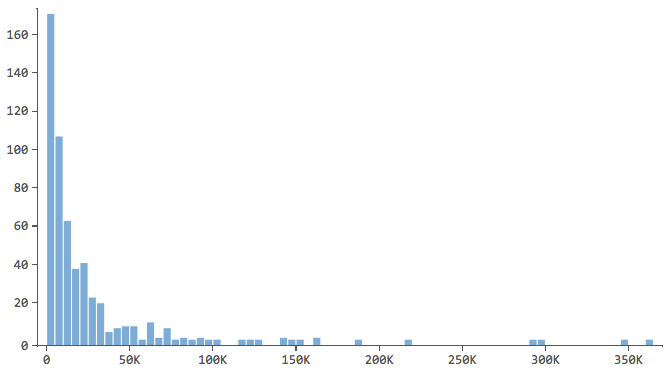
…dove la maggior parte dei dati si trova nei primi bin dell’istogramma. Tali variabili richiederanno in seguito un’attenzione particolare.

3. “Collegare” tutte le possibili variabili esplicative alla variabile di risposta

Stats iQ ordinerà i risultati in base alla forza della relazione statistica. Dai un’occhiata e ottieni un’idea dei risultati, osservando quali variabili sono correlate al “Fatturato” e in che modo.

Se si ha già una buona idea di quali variabili dovrebbero teoricamente guidare l’output (ad es. da precedenti documenti accademici), è opportuno saltare questo passo. Ma se la tua analisi è di natura un po’ più esplorativa (come un’indagine cliente), questo è un passaggio utile e importante.

4. Inizia a creare la regressione

La creazione di un modello di regressione è un processo iterativo. Le tre fasi che seguono saranno eseguite tutte le volte necessarie.

Le tre fasi di costruzione di un modello di regressione

Fase 1: aggiunta o sottrazione di una variabile

Uno alla volta, inizia ad aggiungere nelle variabili che le tue analisi precedenti indicate erano correlate a “Fatturato” (o aggiungi le variabili che hai un motivo teorico da aggiungere). Andare uno alla volta non è strettamente necessario, ma facilita l’identificazione e la risoluzione dei problemi man mano che si procede, aiutandoti a percepire il modello.

Supponiamo di iniziare prevedendo “Fatturato” con “Temperatura”. Si trova un rapporto forte, si valuta il modello e lo si trova soddisfacente (maggiori dettagli in un minuto).

Ricavo = 2,71 * temperatura   –   35

Quindi aggiungi in “Numero di figli che hanno camminato per” e ora il modello di regressione ha due termini, entrambi fattori di probabilità statisticamente significativi. Così:

Ricavi = 2.5 * Temperatura   +   0,3 * NumberOfChildrenWhoWalkedBy   –   12

Quindi aggiungi “Numero di adulti a piedi” e i risultati del modello mostrano ora che “Numero di adulti” è statisticamente significativo nel modello, ma “Numero di bambini” non lo è più. Generalmente si rimuove “Numero di elementi secondari” dal modello. Ora abbiamo:

Fatturato = 2,6 * Temperatura   +   0,4 * NumeroAdultsWhoWalkedBy   –   14

Questo significa che “Numero di adulti” è il miglior predittore di “Fatturato”;, cioè, se sai quanti adulti arrivano, sapere quanti bambini arrivano non aggiunge nuove informazioni – non aiuta a prevedere le vendite.

Forse si ripensa e si ricorda che i bambini non comprano davvero mai la limonata, quindi ha senso che quella variabile non appartenga al modello.

Ma perché è stato statisticamente significativo nel primo modello? Probabilmente perché “Numero di bambini” è correlato al “Numero di adulti“, e dal momento che “Numero di adulti” non era ancora nel modello, “Numero di bambini” fungeva da proxy approssimativo per “Numero di adulti”.

L’interpretazione dei risultati della regressione richiede una buona dose di giudizio, e solo perché una variabile è statisticamente significativa non significa che sia effettivamente causale. Ma aggiungendo e sottraendo con attenzione le variabili, notando come cambia il modello e pensando sempre alla teoria che sta dietro il modello, è possibile mettere in secondo piano relazioni interessanti nei dati.

Fase 2: Valutazione del modello

Ogni volta che si aggiunge o si sottrae una variabile, è necessario valutare l’accuratezza del modello esaminandone R quadro (^R2), AICR e grafici residui. Ogni volta che si modifica il modello, confrontare i nuovi grafici R quadro, AICR e residui con quelli precedenti per determinare se il modello è migliorato o meno.

R-quadrato (^R2)

La metrica numerica per la quantificazione dell’accuratezza di previsione del modello è nota come R quadro, che è compresa tra zero e uno. Lo zero indica che il modello non ha un valore predittivo e uno indica che il modello prevede perfettamente tutto.

Ad esempio, il modello a sinistra è più preciso di quello a destra; cioè, se conoscete “Temperatura”, avete un’ipotesi abbastanza buona su quale “Fatturato” sarà a sinistra, ma non davvero a destra.

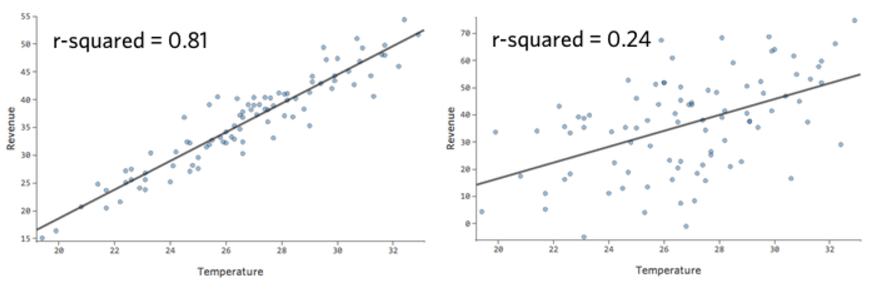
Non esiste una definizione fissa di R quadro “buono”. In alcune impostazioni potrebbe essere interessante vedere qualsiasi effetto, mentre in altre il modello potrebbe essere inutile a meno che non sia altamente accurato.

Ogni volta che si aggiunge una variabile, R quadro salirà, in modo che il raggiungimento dell’R quadro più alto possibile non sia l’obiettivo; piuttosto, si desidera bilanciare l’accuratezza del modello (R quadro) con la sua complessità (in genere, il numero di variabili in esso contenute).

AICR

L’AICR è una metrica che bilancia l’accuratezza con la complessità: una maggiore accuratezza porta a punteggi migliori, una maggiore complessità (più variabili) porta a punteggi peggiori. Meglio il modello con il basso AICR.

Si noti che la metrica AICR è utile solo per confrontare gli AICR di modelli che hanno lo stesso numero di righe di dati e la stessa variabile di output.

Intervalli di previsione

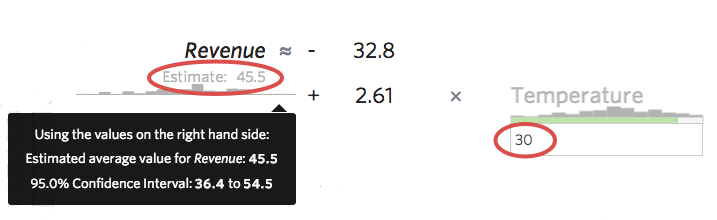
Un altro modo utile per percepire l’accuratezza del tuo modello è incollare i valori campione nella tua formula e vedere l’intervallo di previsione che Stats iQ calcola. Ad esempio, se si inserisce il numero 30 nella formula, Stats iQ ti dirà che il valore previsto è 45,5, ma l’intervallo di confidenza al 95% è da 36,4 a 54,5, il che significa che potresti essere sicuro al 95% che se domani si rivelasse essere di 30 gradi, otterresti tra $ 36,40 e $ 54,50 in “ricavi”. È possibile immaginare un modello più accurato in cui l’intervallo di previsione era una banda stretta come da $44 a $48, o un modello meno accurato in cui l’intervallo era largo, come $20 a $72.

Questo approccio è utile solo quando le trame residue appaiono in buona salute (vedi sotto), altrimenti saranno imprecise.

Resti

I residui sono lo strumento diagnostico principale per valutare e migliorare la regressione, pertanto è disponibile un’intera sezione separata sull’interpretazione dei residui per migliorare il modello. Si apprenderà o si aggiornerà la memoria sui residui, su come utilizzarli per valutare e migliorare il modello e su come riflettere sull’accuratezza del modello.

Ti consigliamo di leggerlo per intero, in quanto coprirà tutto il resto di cui hai bisogno per produrre un ottimo modello. Ma si può sempre tornare a parlarne, ovviamente.

Fase 3: Modificare il modello di conseguenza

Se la valutazione del modello lo ha giudicato soddisfacente, si è fatto oppure si può tornare alla Fase 1 e inserire più variabili.

Se la tua valutazione trova il modello mancante, utilizzerai gli avvisi di Stats iQ e la sezione diagnostica residua per risolvere i problemi.

Quando si modifica il modello, notare continuamente le modifiche R quadro, AICR e diagnostica residua e decidere se le modifiche apportate aiutano o danneggiano il modello.

FAQ