Interpretazione dei tracciati residui per migliorare la regressione
Quando esegui una regressione, Stats iQ calcola e traccia automaticamente i residui per aiutarti a comprendere e migliorare il tuo modello di regressione. Leggi qui di seguito per scoprire tutto ciò che devi sapere sull’interpretazione dei residui (comprese le definizioni e gli esempi).
Osservazioni, previsioni e residui
Per dimostrare come interpretare i residui, utilizzeremo un set di dati di uno stand di limonata, in cui ogni riga era un giorno di “Temperatura” e “Ricavo”.
| Temperatura (Celsius) | Ricavo |
|---|---|
| 28,2 | 44 $ |
| 21,4 | 23 $ |
| 32,9 | 43 $ |
| 24 | 30 $ |
| ecc. | ecc. |
L’equazione di regressione che descrive la relazione tra “Temperatura” e “Ricavo” è:
Ricavo = 2,7 * Temperatura – 35
Diciamo che un giorno allo stand di limonata era di 30,7 gradi e il “Ricavo” era di 50 $. 50 è il tuo risultato osservato o effettivo , il valore che si è effettivamente verificato.
Quindi se inseriamo 30,7 al nostro valore per “Temperatura”…
Ricavo= 2,7 * 30,7 – 35
Ricavo = 48
…otteniamo 48 $. Questo è il valore previsto per quel giorno, noto anche come il valore per il “Ricavo” che l’equazione di regressione avrebbe previsto in base alla “Temperatura”.
Ovviamente, il tuo modello non è sempre perfettamente giusto. In questo caso, la previsione presenta uno scarto di 2; quella differenza, 2, è chiamata residuo. Il residuo è la parte rimasta quando si sottrae il valore previsto dal valore osservato.
Residuo = Osservato – Previsto
È possibile immaginare che ogni riga di dati abbia ora, in aggiunta, un valore previsto e uno residuo.
| Temperatura (Celsius) |
Ricavo (Osservato) |
Ricavo (Previsto) |
Residuo (Osservato – Previsto) |
|---|---|---|---|
| 28,2 | 44 $ | 41 $ | 3 $ |
| 21,4 | 23 $ | 23 $ | 0 $ |
| 32,9 | 43 $ | 54 $ | – 11 $ |
| 24,0 | 30 $ | 29 $ | 1 $ |
| ecc. | ecc. | ecc. | ecc. |
Utilizzeremo i valori osservati, previsti e residui per valutare e migliorare il modello.
Comprendere l’accuratezza di osservato rispetto a previsto
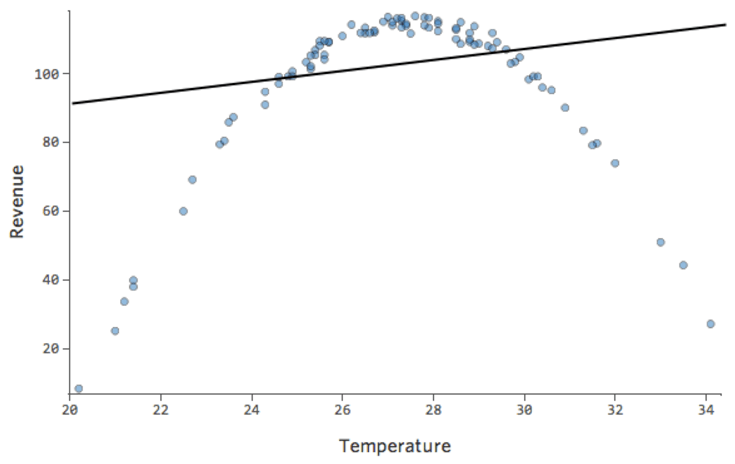
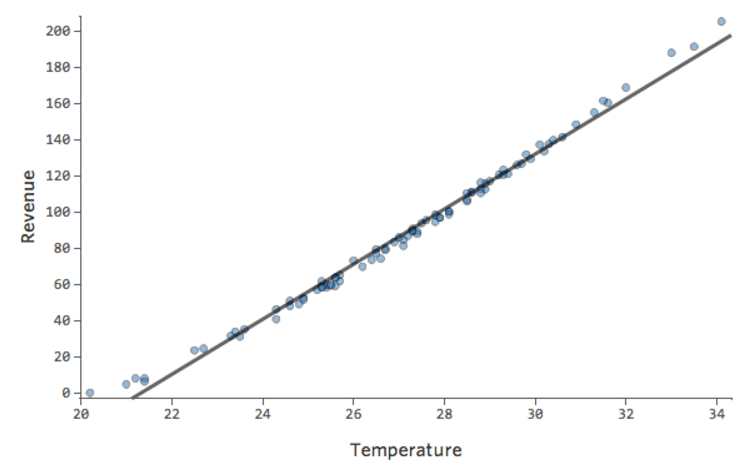
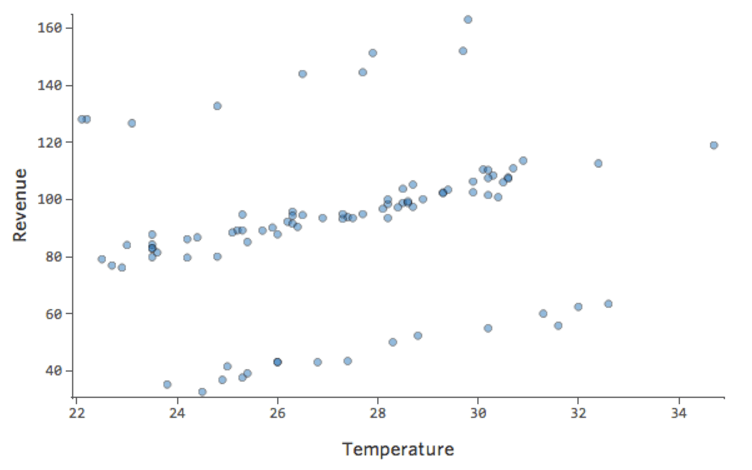
In un modello semplice come questo, con due sole variabili, è possibile avere un’idea di quanto il modello sia accurato semplicemente correlando “Temperatura” a “Ricavo”. Qui di seguito viene eseguita la stessa regressione su due diversi stand di limonata, uno in cui il modello è molto accurato e uno in cui non lo è:
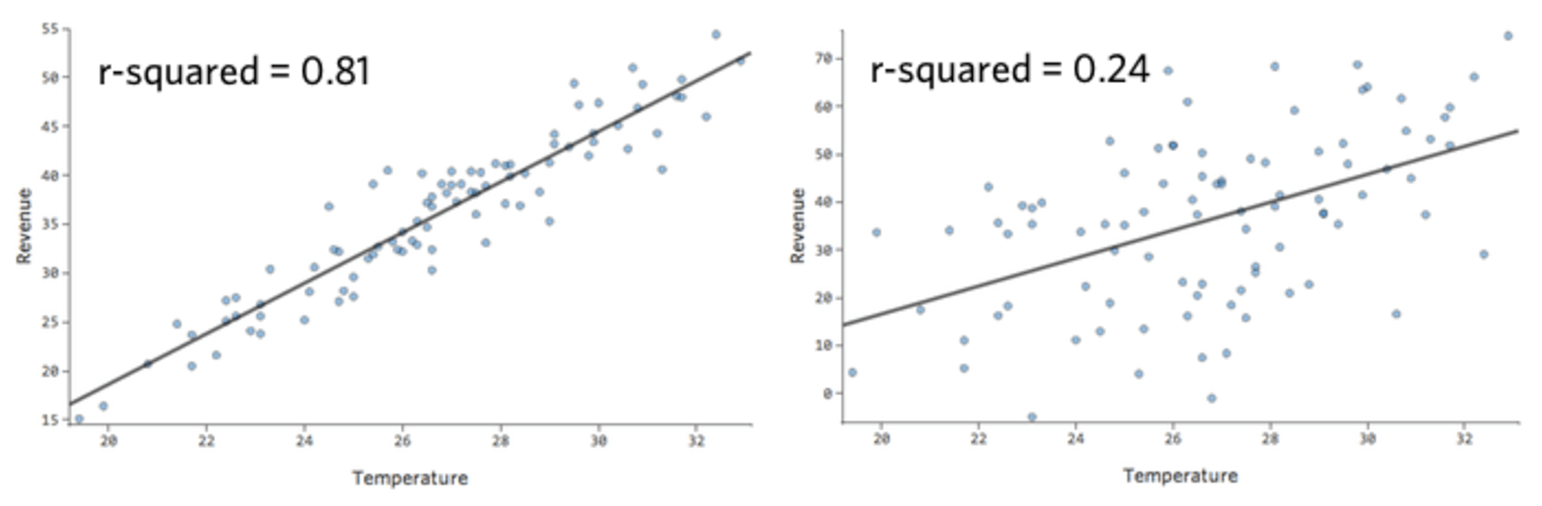
È chiaro che per entrambi gli stand di limonata, una “Temperatura” più alta è associata ad un “Ricavo” più alto. Ma a una data “Temperatura”, sarebbe possibile prevedere il “Ricavo” dello stand di limonata di sinistra in modo molto più accurato rispetto allo stand della limonata di destra, il che significa che il modello è molto più accurato.
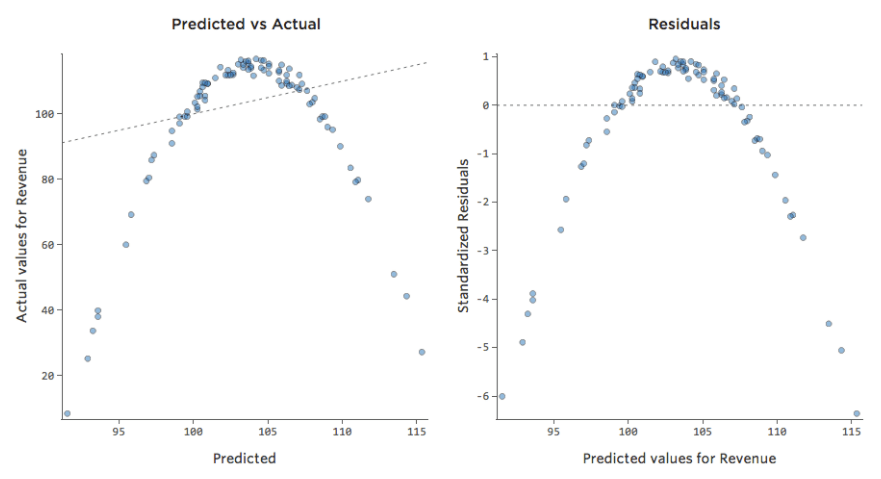
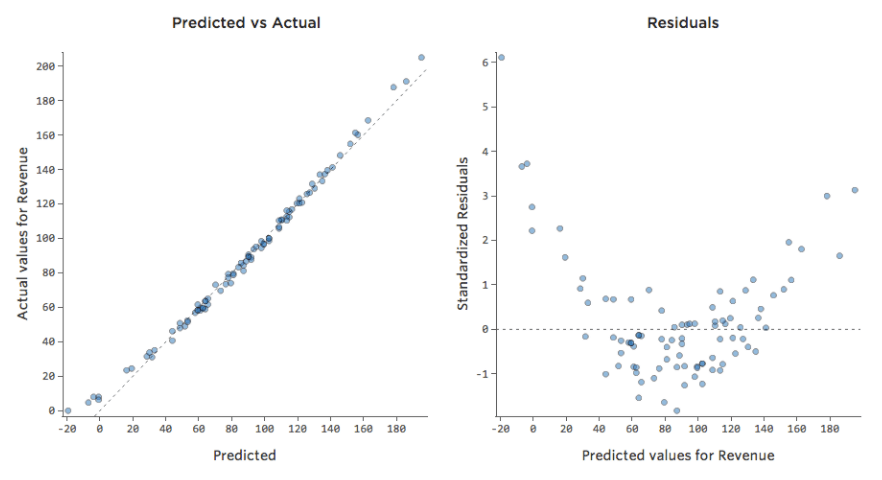
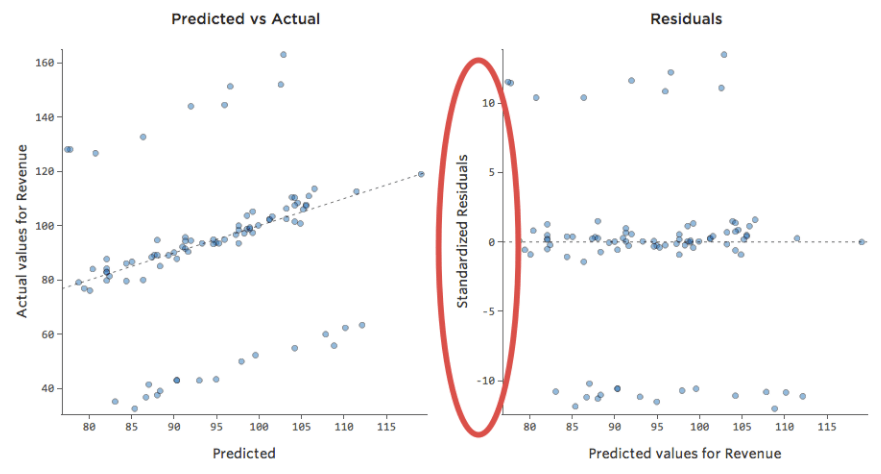
Tuttavia, la maggior parte dei modelli ha più di una variabile esplicativa, e non è pratico rappresentare più variabili in un grafico del genere. Pertanto, tracciamo i valori previsti rispetto ai valori osservati per questi stessi set di dati.
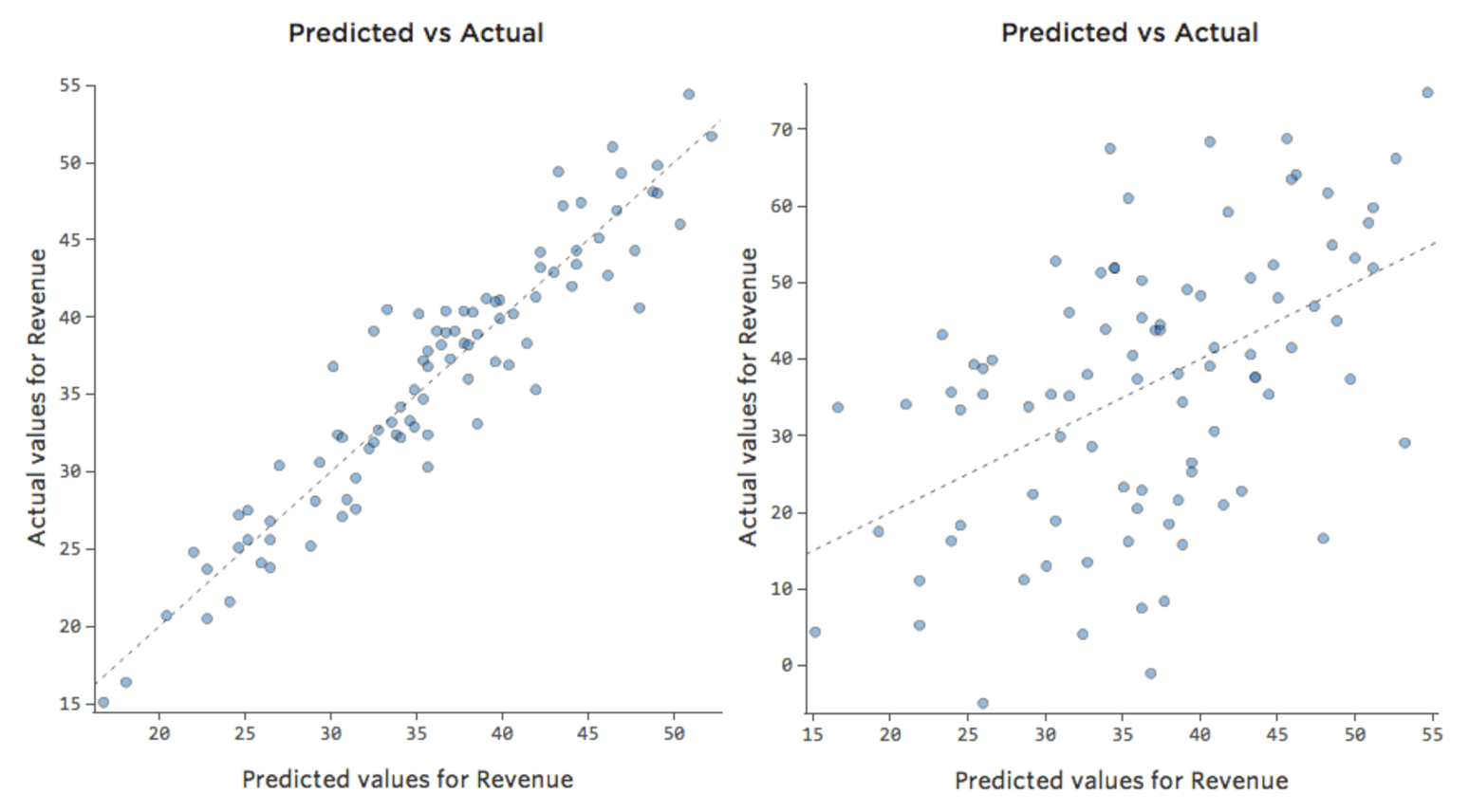
Anche in questo caso, il modello per il grafico a sinistra è molto accurato; esiste una forte correlazione tra le previsioni del modello e i suoi risultati effettivi. Il modello del grafico all’estrema destra è il contrario; le previsioni del modello sono tutt’altro che ottime.
Nota: questi grafici sembrano proprio come la “Temperatura” rispetto al “Ricavo” che si trovano sopra, ma l’asse delle x è previsto “Ricavo” invece di “Temperatura“. Questo è comune quando l’equazione di regressione ha una sola variabile esplicativa. Tuttavia, più spesso, si avranno più variabili esplicative, e questi grafici avranno un aspetto piuttosto diverso da un tracciato di una qualsiasi variabile esplicativa rispetto a “Ricavo”.
Esaminare previsto rispetto a residuo (“Il tracciato residuo”)
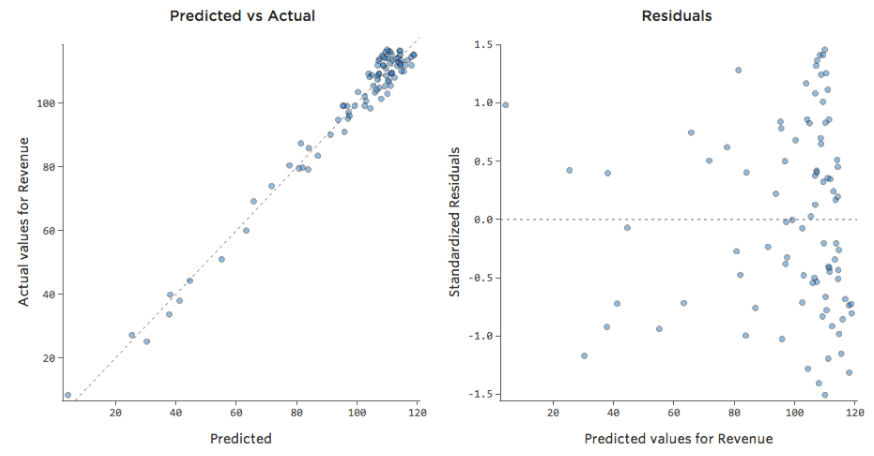
Il modo più utile per tracciare i residui, tuttavia, è con i valori previsti sull’asse delle x e i residui sull’asse delle y.
(Stats iQ presenta i residui come residui standardizzati, il che significa che ogni tracciato residuo che si guarda con un qualsiasi modello è sullo stesso asse delle y standardizzato.)
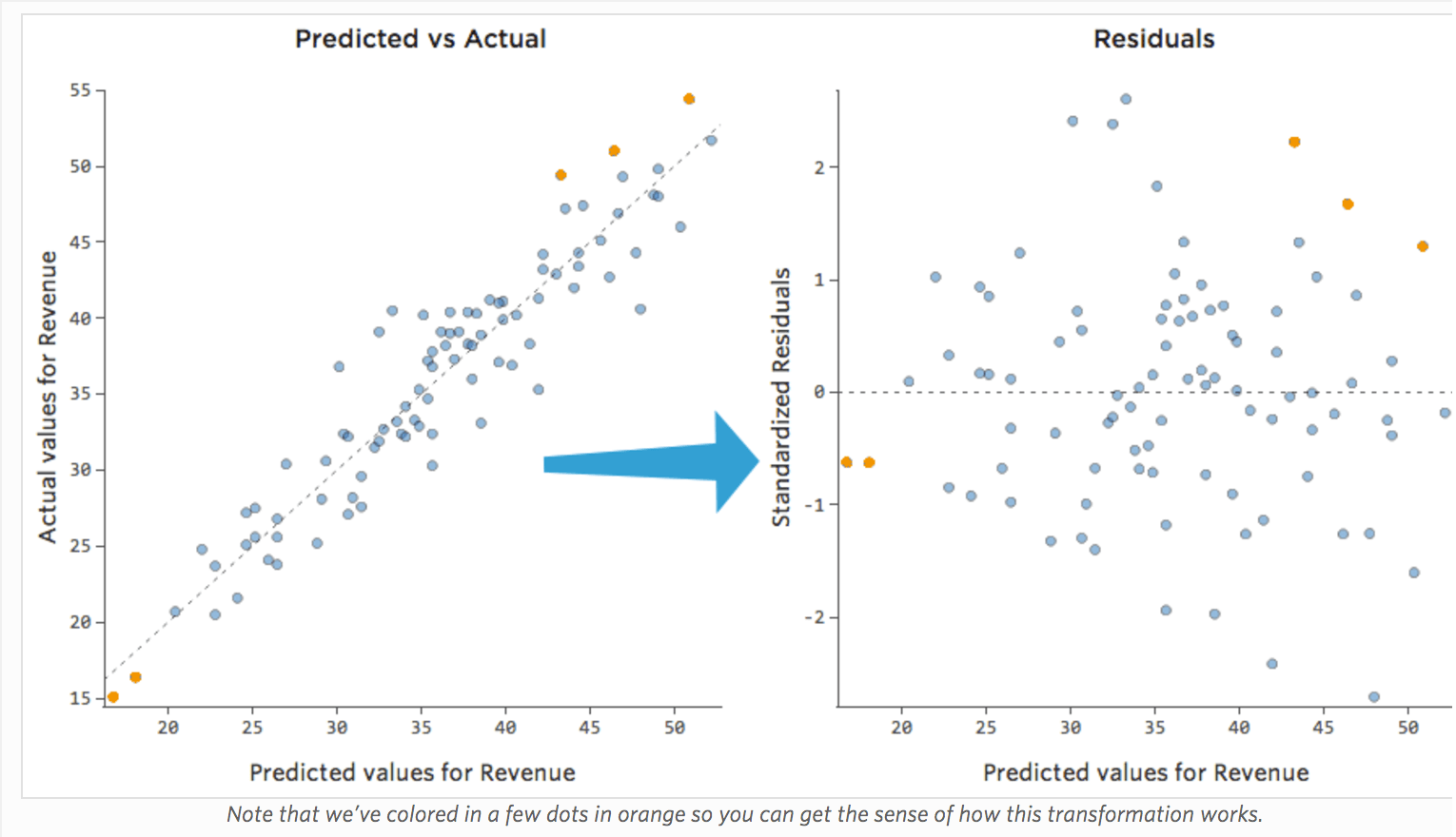
Nel tracciato a destra, ogni punto è un giorno, in cui la previsione effettuata dal modello è sull’asse delle x e l’accuratezza della previsione è sull’asse delle y. La distanza dalla linea a 0 indica quanto la previsione era negativa per quel valore.
Poiché…
Residuo = Osservato – Previsto
…valori positivi per il residuo (sull’asse y) indicano che la previsione era troppo bassa, e i valori negativi indicano che la previsione era troppo alta; 0 indica che la stima era esattamente corretta.
Idealmente, il tracciato dei residui ha il seguente aspetto:
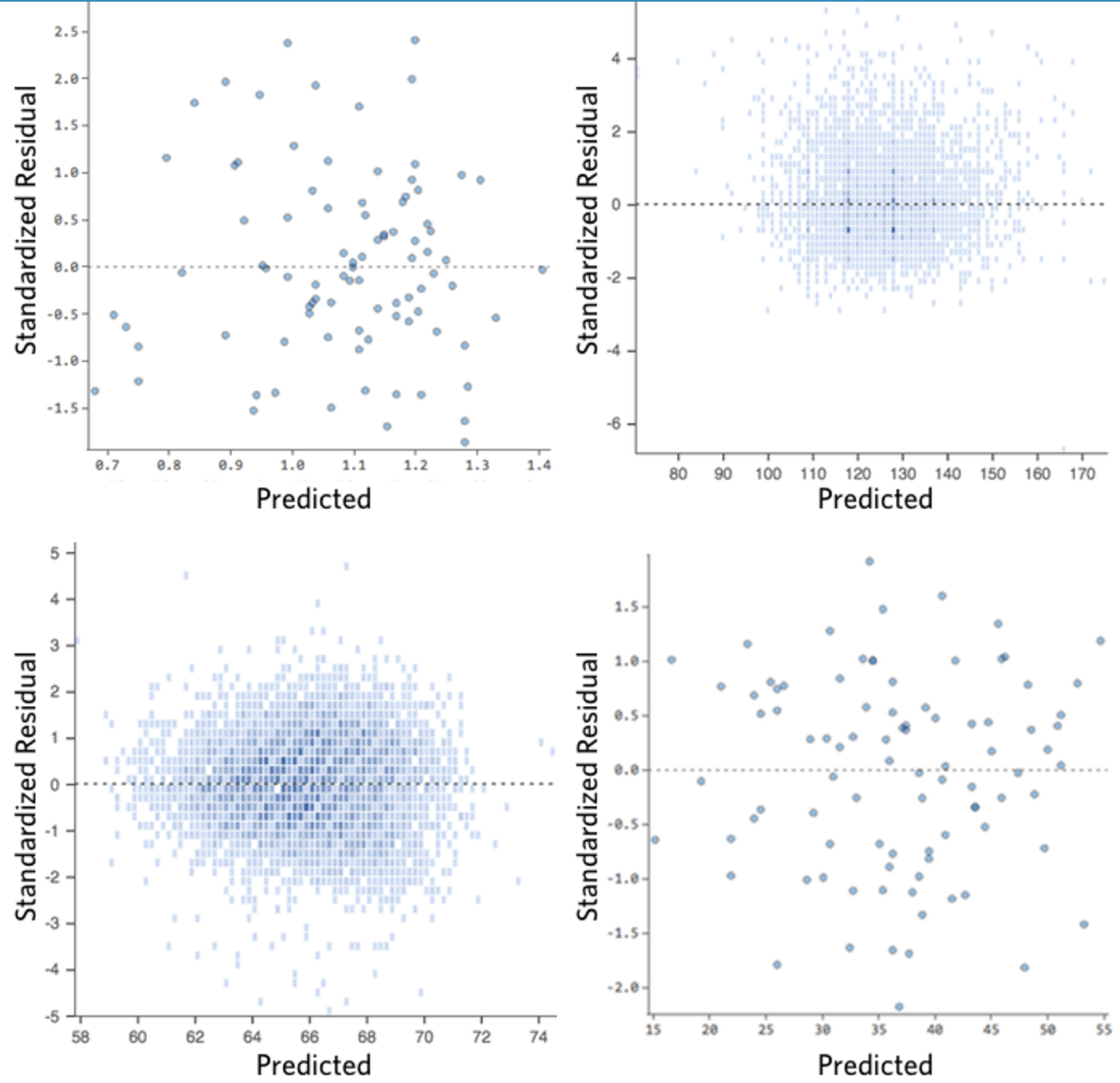
Cioè,
(1) sono distribuiti in maniera perfettamente simmetrica, tendendo a concentrarsi intorno alla metà del tracciato.
(2) sono raggruppati intorno alle singole cifre inferiori dell’asse y (ad esempio, 0,5 o 1,5, non 30 o 150)
(3) in generale, non ci sono modelli chiari.
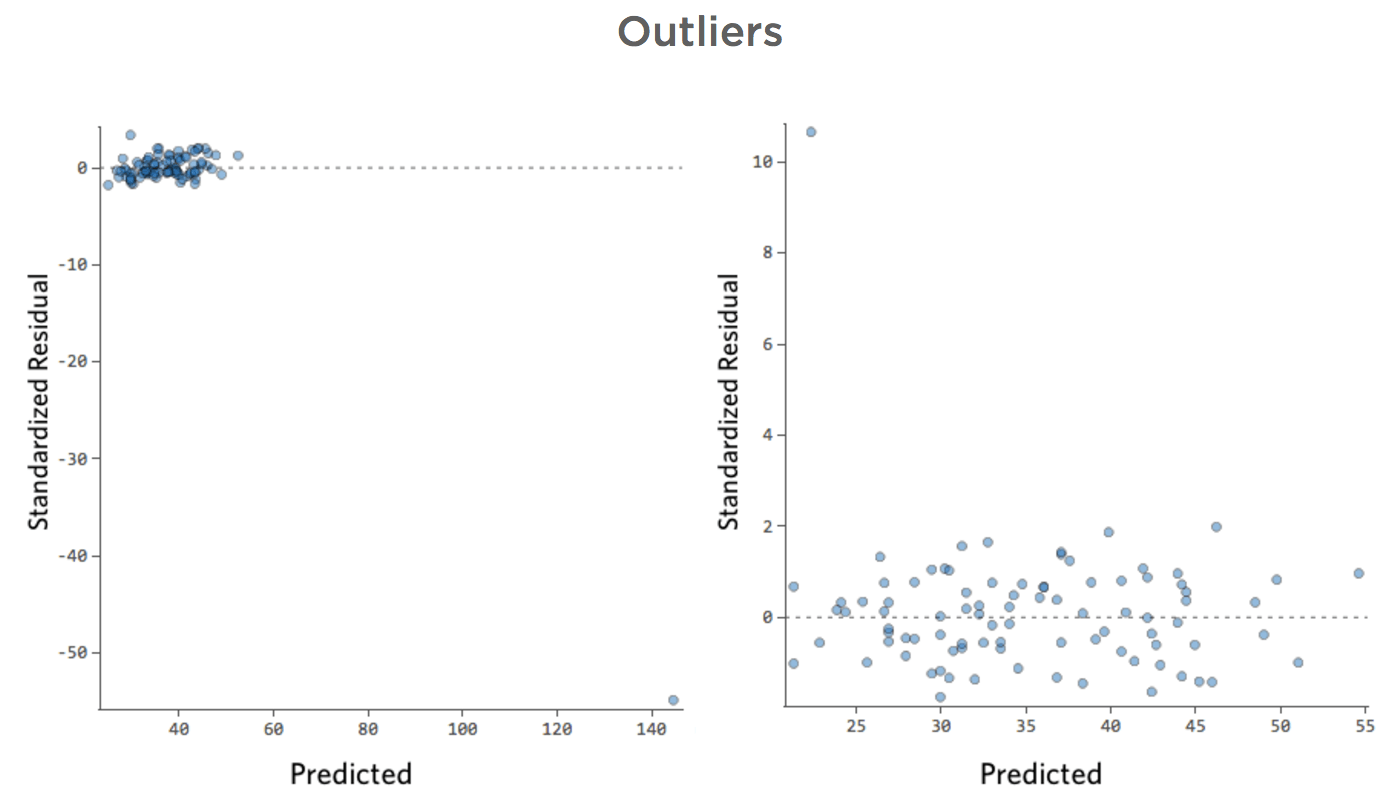
Ecco alcuni tracciati residui che non soddisfano tali requisiti:
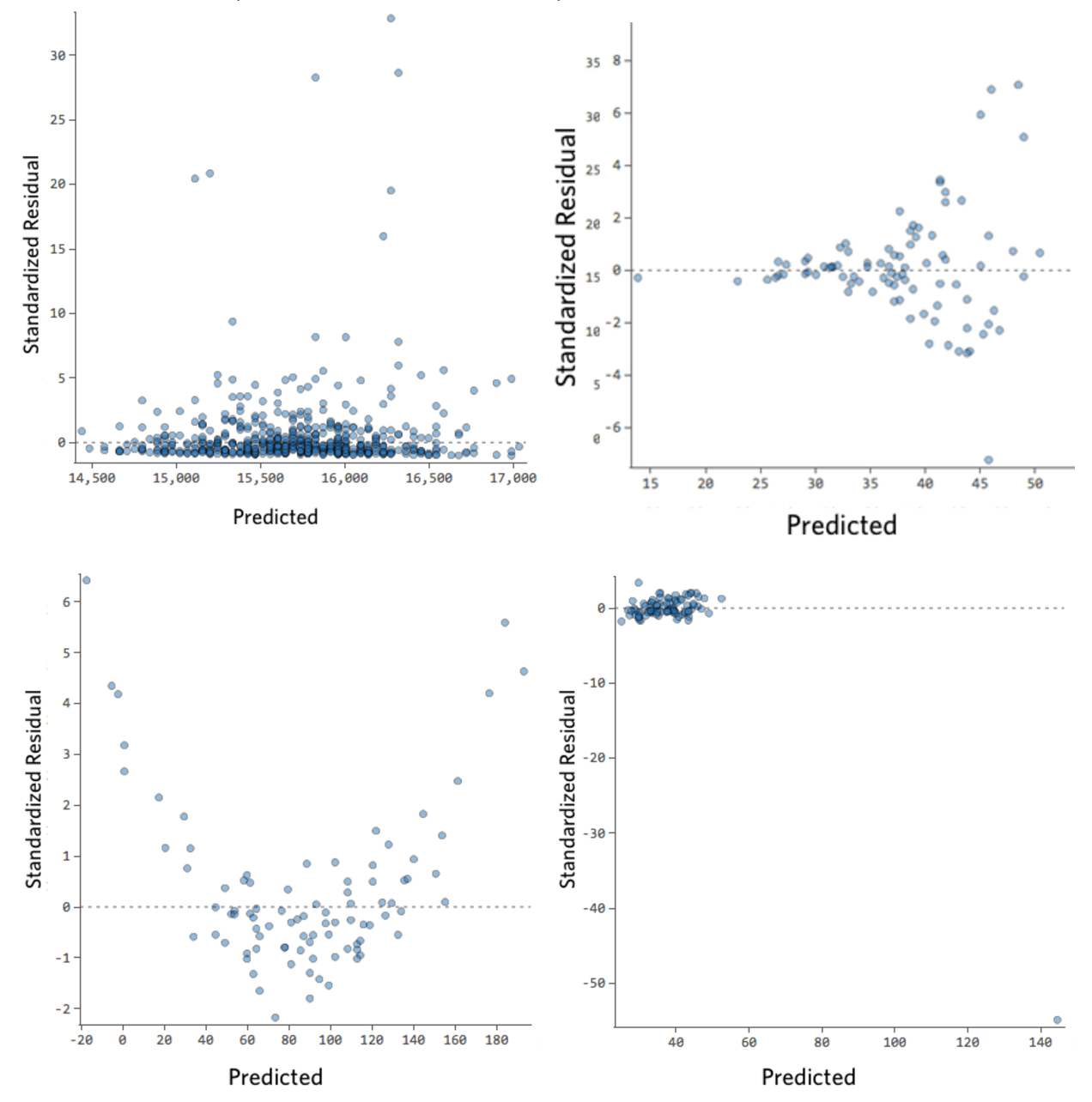
Questi tracciati non sono distribuiti in modo uniforme verticalmente, hanno un valore fuori dalla norma o hanno una forma chiara.
Se è possibile rilevare un modello chiaro o una tendenza nei residui, il modello ha margini di miglioramento.
Tra un secondo andremo ad analizzare il perché e cosa fare al riguardo.
Tracciato residuo Q-Q normale:
Fai clic su Mostra diagramma residuo Q-Q normale per visualizzare un diagramma Q-Q che valuta la distorsione dei dati e l’adattamento del modello. Questo grafico mostra i residui standardizzati sull’asse delle y e i quantili teorici sull’asse delle x.
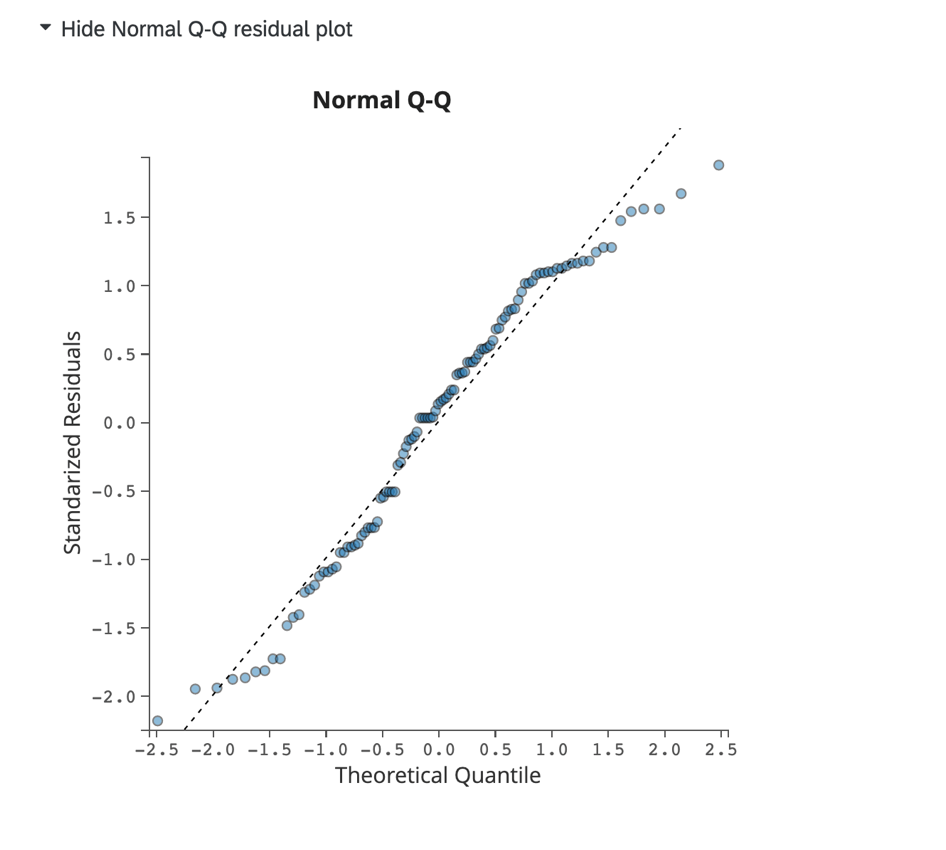 I dati che si allineano strettamente alla linea tratteggiata indicano una distribuzione normale. Se i punti si scostano drasticamente dalla linea, è possibile prendere in considerazione la possibilità di adattare il modello aggiungendo o rimuovendo altre variabili nel modello di regressione.
I dati che si allineano strettamente alla linea tratteggiata indicano una distribuzione normale. Se i punti si scostano drasticamente dalla linea, è possibile prendere in considerazione la possibilità di adattare il modello aggiungendo o rimuovendo altre variabili nel modello di regressione.
Quanto è importante che il mio modello non è perfetto?
Quanto dovresti essere preoccupato se il tuo modello non è perfetto, se i residui sembrano un po’ non adeguati? Dipende da te.
Se stai pubblicando la tua tesi in fisica delle particelle, probabilmente vuoi assicurarti che il tuo modello sia il più possibile accurato dal punto di vista umano. Se stai cercando di eseguire un’analisi rapida e grezza dello stand di limonata di tuo nipote, un modello meno che perfetto potrebbe essere abbastanza adeguato da rispondere a qualsiasi tua domanda (ad esempio, se “Temperatura” sembra influire su “Ricavo”).
Il più delle volte un modello decente è meglio di nessun modello affatto. Prendi quindi il tuo modello, cerca di migliorarlo e quindi decidi se l’accuratezza è abbastanza adeguata da essere utile per i tuoi scopi.
Esempio di tracciati residui e relative diagnosi
Se non sei sicuro di cosa sia un residuo, prenditi cinque minuti per leggere quanto sopra, quindi torna qui.
Qui di seguito una galleria di tracciati residui non adeguati. Il residuo potrebbe essere di un tipo specifico riportato di seguito o una combinazione.
Se il tuo sembra uno dei seguenti, clicca su quel residuo per capire cosa sta succedendo e imparare a risolverlo.
(In tutto il processo utilizzeremo il “Ricavo” dello stand di limonata rispetto alla “Temperatura” di quel giorno come set di dati esemplificativo).
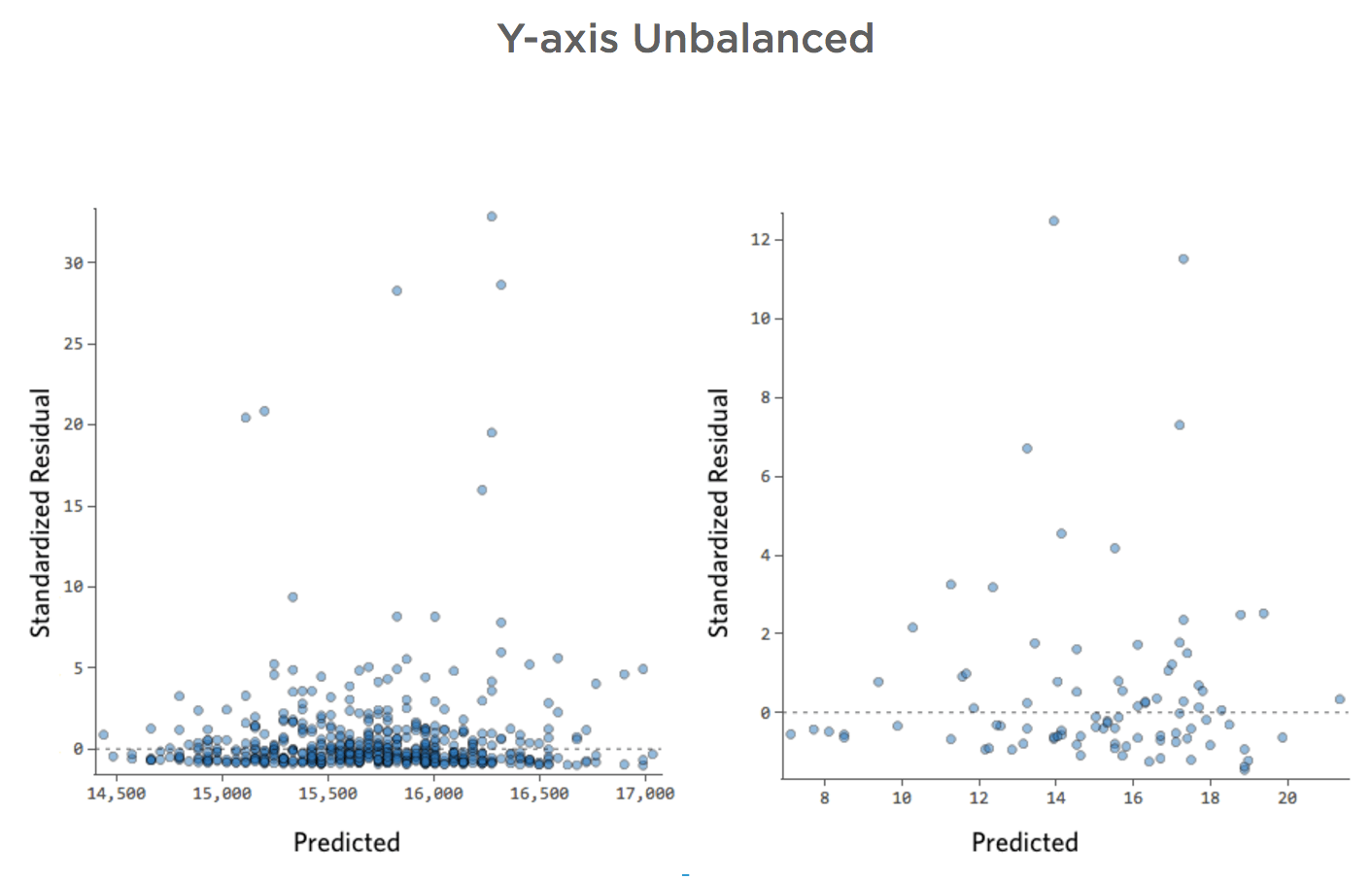
Asse delle y sbilanciato
- Mostra dettagli su questo tracciato e su come risolverlo.
-
Problema
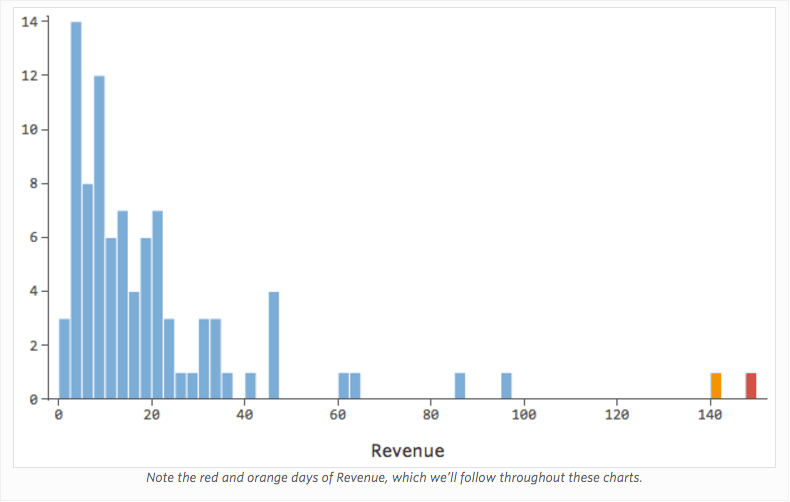
Immagina che per qualsiasi motivo, il tuo stand di limonata abbia solitamente un ricavo basso, ma ogni tanto si hanno giorni con guadagni molto alti, tali che “Ricavo” appariva come…
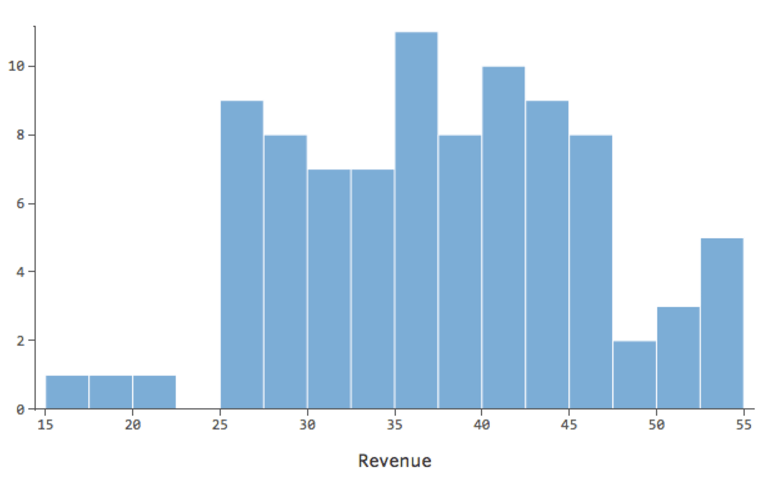
…invece di qualcosa di più simmetrico e a campana come questo:
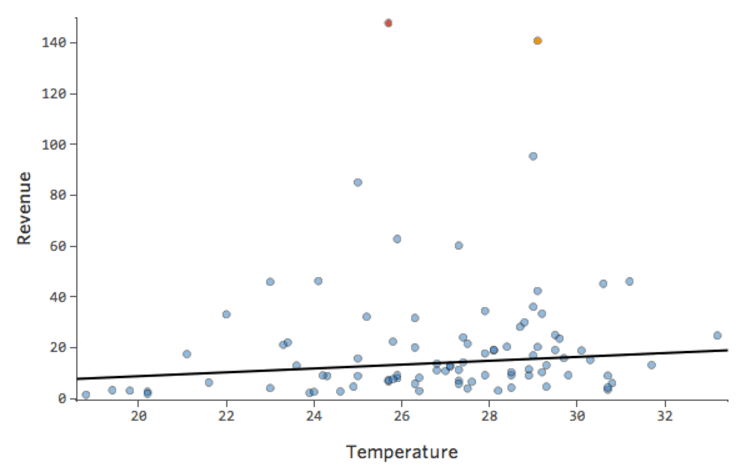
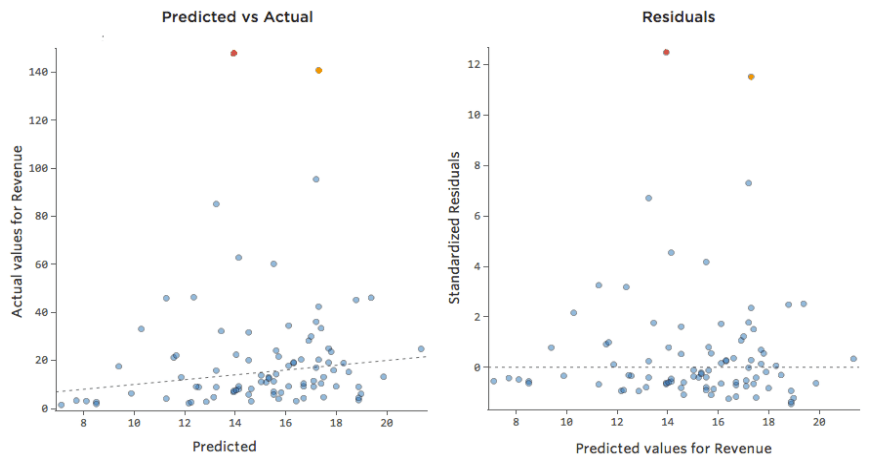
Quindi “Temperatura” rispetto a “Ricavo” potrebbe apparire così, con la maggior parte dei dati raggruppati nella parte inferiore…
La linea nera rappresenta l’equazione del modello, la previsione del modello della relazione tra “Temperatura” e “Ricavo”. Guarda sopra ogni previsione fatta dalla linea nera per una data “Temperatura” (ad esempio, a “Temperatura” 30, si prevede che “Ricavo” sia circa 20). Si vede che la maggior parte dei punti si trovano sotto la linea (ovvero, la previsione era troppo alta), ma alcuni punti si trovano molto al di sopra della linea (ovvero, la previsione era decisamente troppo bassa).
Traducendo gli stessi dati nei tracciati diagnostici, la maggior parte delle previsioni dell’equazione sono un po’ troppo alte, e quindi alcune sarebbero decisamente troppo basse.
Implicazioni
Questo significa quasi sempre che il modello può essere reso significativamente più accurato. Nella maggior parte dei casi, si noterà che il modello era direzionalmente corretto ma abbastanza inaccurato rispetto a una versione migliorata. Non è raro risolvere un problema del genere e di conseguenza vedere il salto a R-quadrato del modello da 0,2 a 0,5 (su una scala da 0 a 1).
Come risolvere il problema
- La soluzione a questo problema è quasi sempre quella di trasformare i tuoi dati, in genere la tua variabile di risposta .
- È anche possibile che nel modello manchi una variabile.
Eteroschedasticità
- Mostra dettagli su questo tracciato e su come risolverlo.
-
Problema
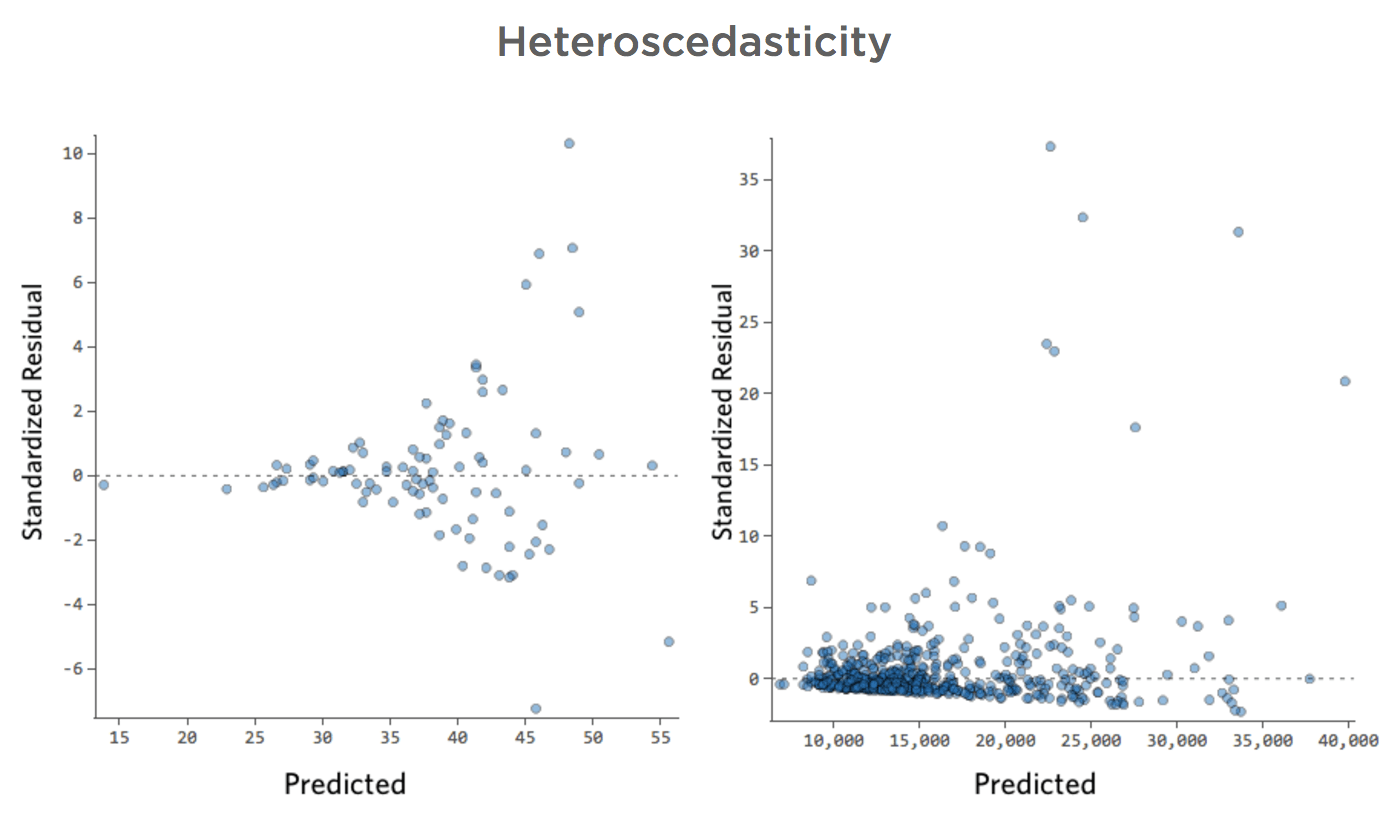
Questi tracciati mostrano “eteroschedasticità”, il che significa che i residui diventano più grandi quando la previsione si sposta da piccola a grande (o da grande a piccola).
Immagina che nei giorni freddi la quantità di ricavo sia molto consistente, ma nei giorni più caldi, a volte il ricavo è molto alto e a volte è molto basso.
Si vedrebbero tracciati come questi:
Implicazioni
Questo non crea un problema in modo intrinseco, ma spesso è un indicatore della possibilità di migliorare il modello.
L’unica eccezione in questo caso è che se la dimensione del campione è inferiore a 250 e non è possibile risolvere il problema utilizzando quanto riportato qui di seguito, i valori p potrebbero essere un po’ più alti o bassi rispetto a quelli previsti, quindi una variabile corretta al limite della significatività potrebbe finire erroneamente sul lato sbagliato di quel limite. Tuttavia, i coefficienti di regressione (il numero di unità “Ricavo” cambia quando “Temperatura” aumenta di uno) saranno comunque accurati.
Come risolvere il problema
- La soluzione più frequentemente positiva è trasformare una variabile.
- Spesso l’eteroschedasticità indica che manca una variabile.
Non lineare
- Mostra dettagli su questo tracciato e su come risolverlo.
-
Problema
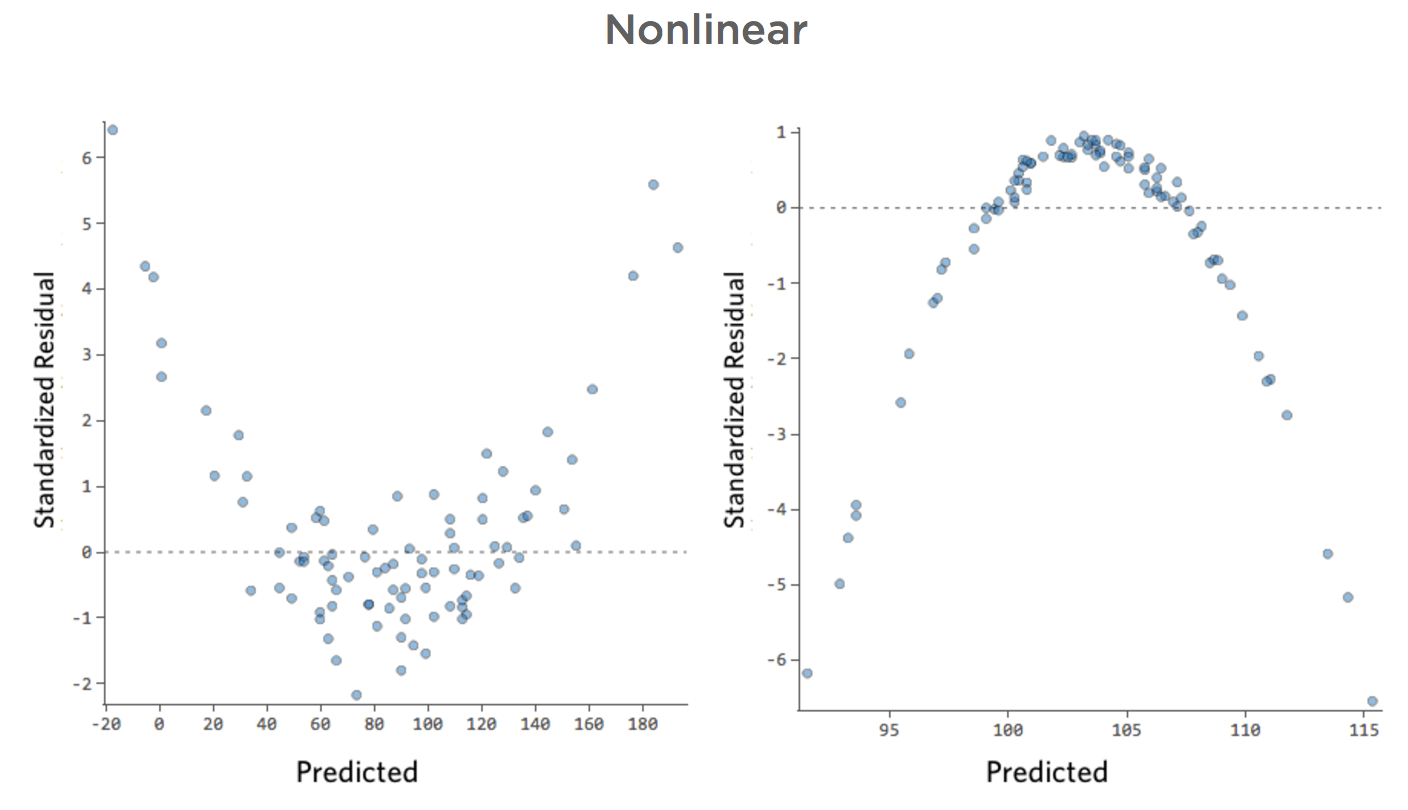
Immagina che sia difficile vendere limonata nei giorni freddi, facile venderla nei giorni caldi e difficile venderla in giornate molto calde (magari perché nessuno esce di casa nei giorni caldissimi).
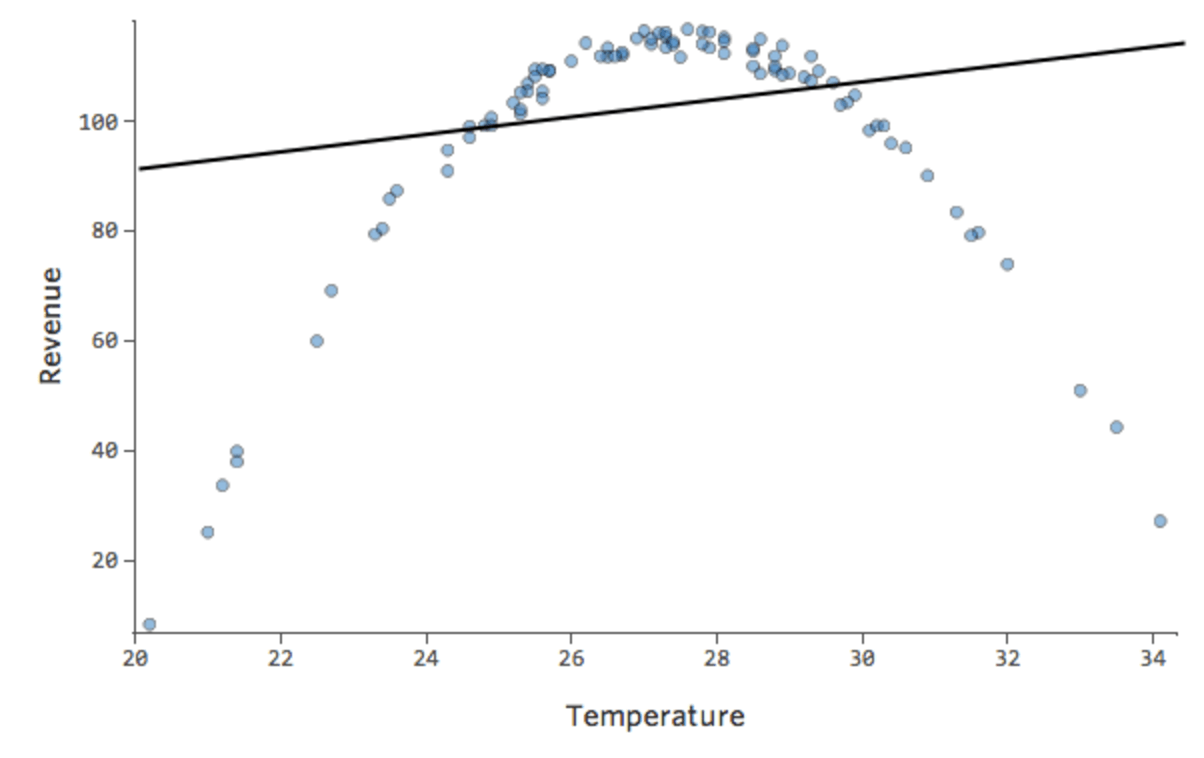
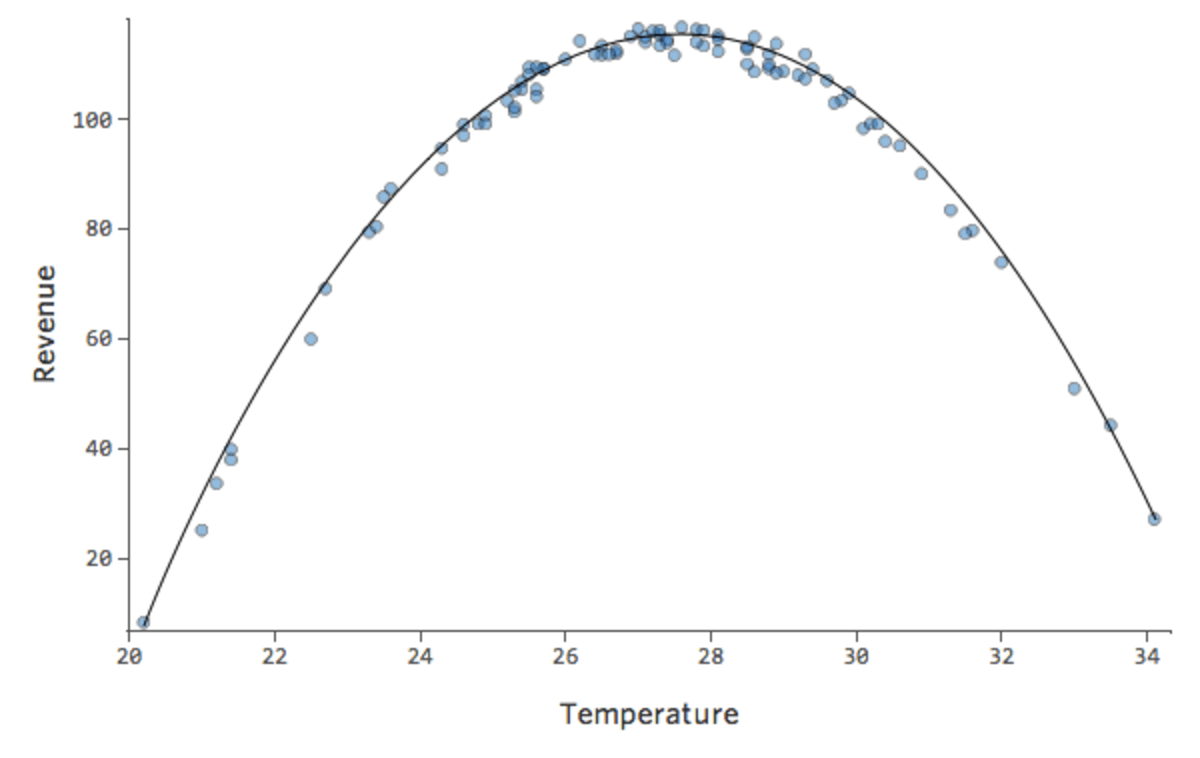
Il tracciato avrebbe il seguente aspetto:
Il modello, rappresentato dalla linea, è terribile. Le previsioni sarebbero lontane, il che significa che il modello non rappresenta in modo accurato la relazione tra “Temperatura” e “Ricavo”.
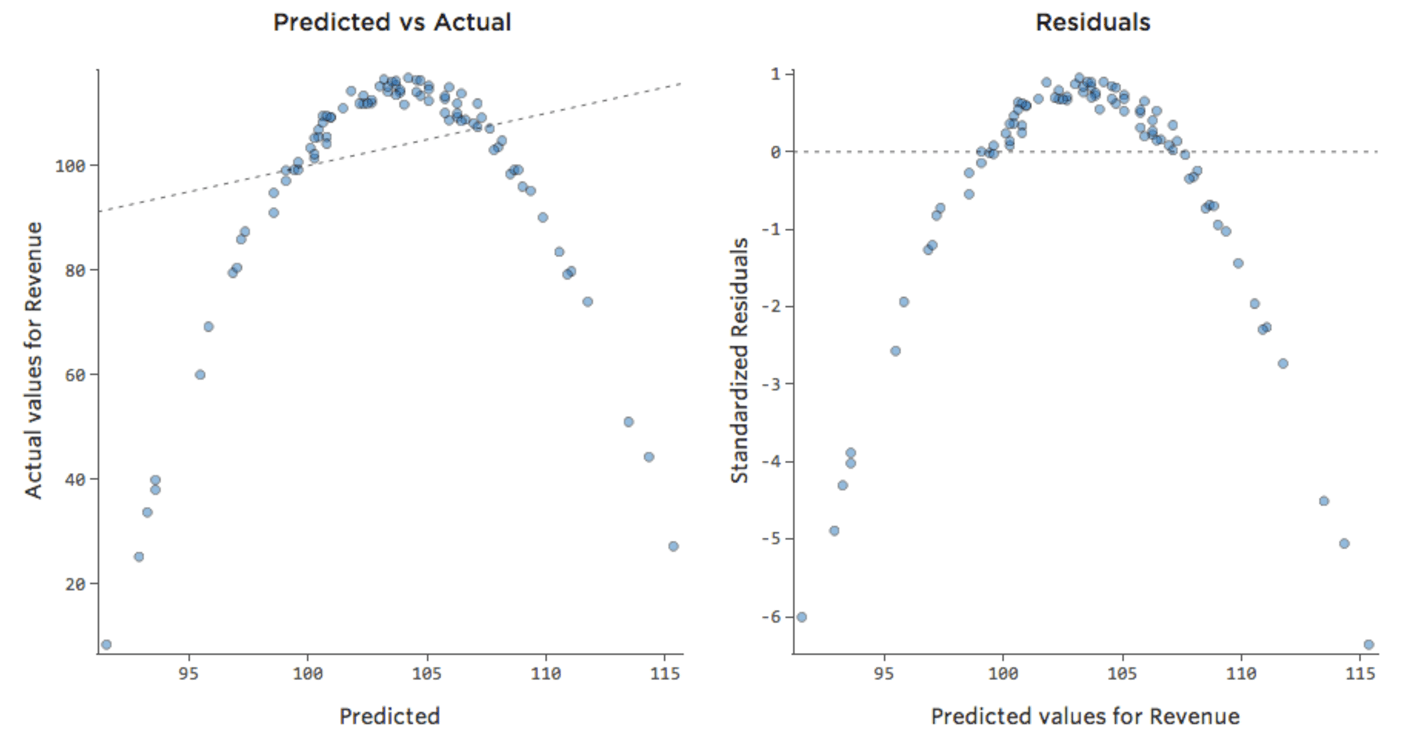
Di conseguenza, i residui apparire nel modo seguente:
Implicazioni
Se il modello è lontano, come nell’esempio precedente, le previsioni saranno piuttosto prive di valore (e si noterà un R-quadrato molto basso, come l’R-quadrato di 0,027 per quanto sopra).
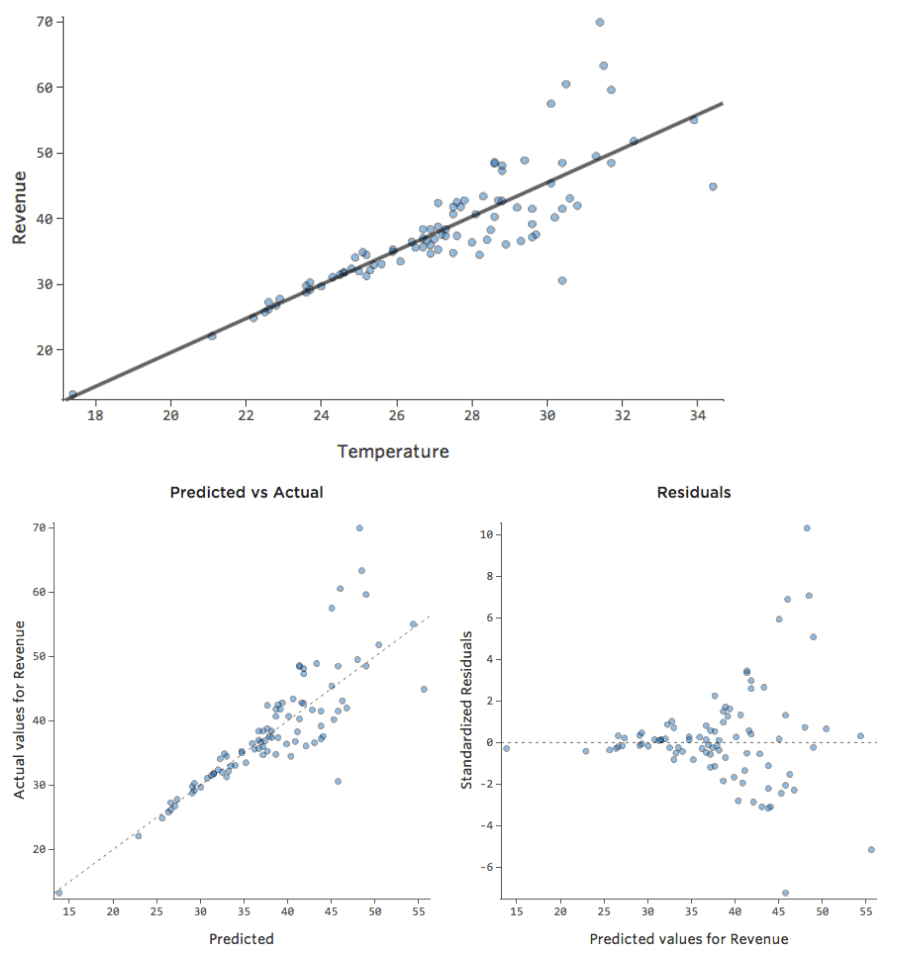
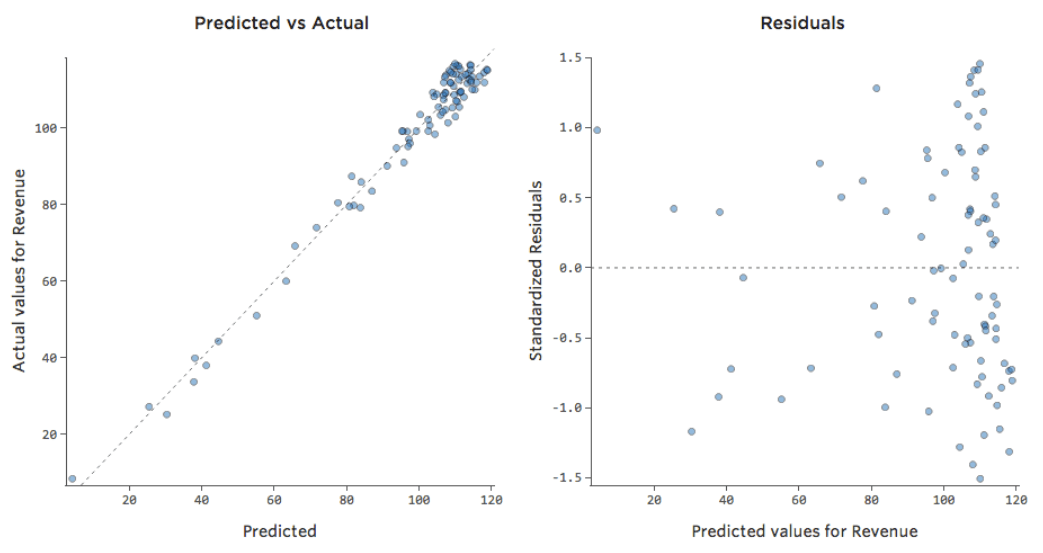
Altre volte un adattamento leggermente non ottimale ti darà comunque un buon senso generale della relazione, anche se non è perfetta, come la seguente:
Quel modello sembra molto accurato. Se si guarda con attenzione (o se si osservano i residui), è possibile dire che qui c’è un po’ di un modello, che i punti sono su una curva a cui la linea non corrisponde del tutto.
È importante? Dipende da te. Se vuoi ottenere una rapida comprensione della relazione, la tua linea retta è un’approssimazione abbastanza decente. Se intendi utilizzare questo modello per la previsione e non per la spiegazione, è probabile che il modello più accurato possibile tenga conto di tale curva.
Come risolvere il problema
- A volte modelli come questo indicano che una variabile deve essere trasformata.
- Se il modello è effettivamente chiaro come questi esempi, probabilmente è necessario creare un modello non lineare (non è così difficile come sembra).
- Oppure, come sempre, è possibile che il problema sia una variabile mancante.
Valori fuori norma
- Mostra dettagli su questo tracciato e su come risolverlo.
-
Problema
E se uno dei tuoi datapoint avesse una “Temperatura” di 80 invece dei normali 20 e 30? I tuoi tracciati apparirebbero nel seguente modo:
Questa regressione ha un datapoint periferico su una variabile di input, “Temperatura” (i valori fuori norma su una variabile di input sono noti anche come “punti di leva”).
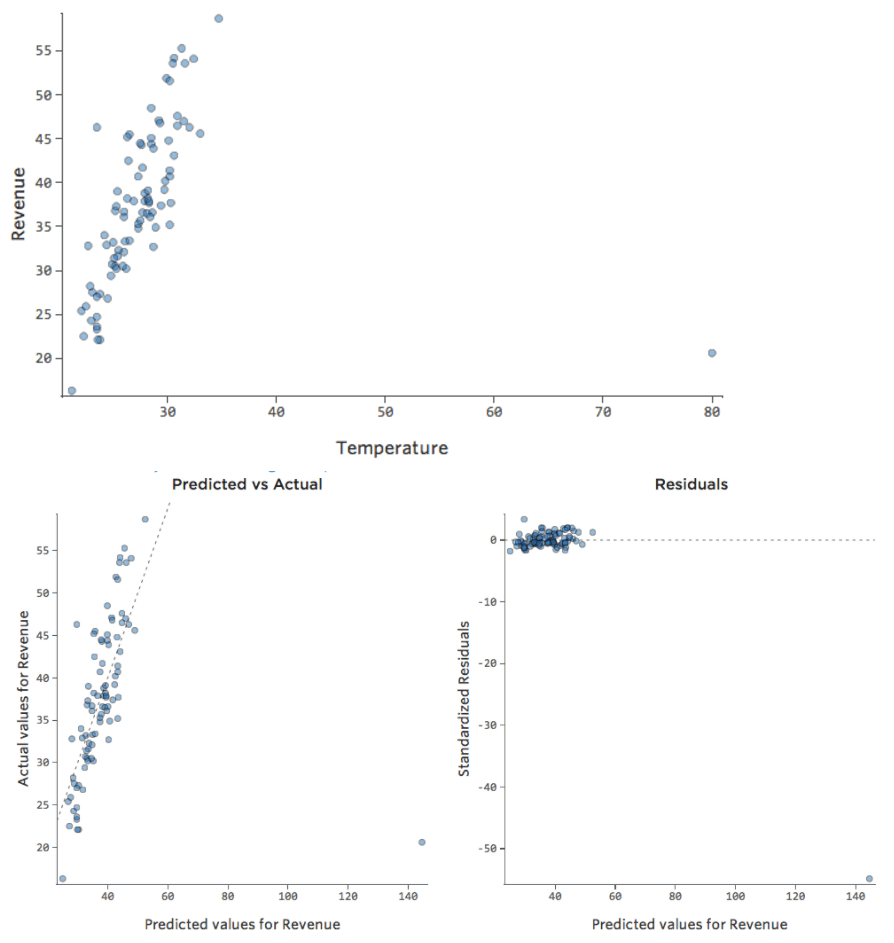
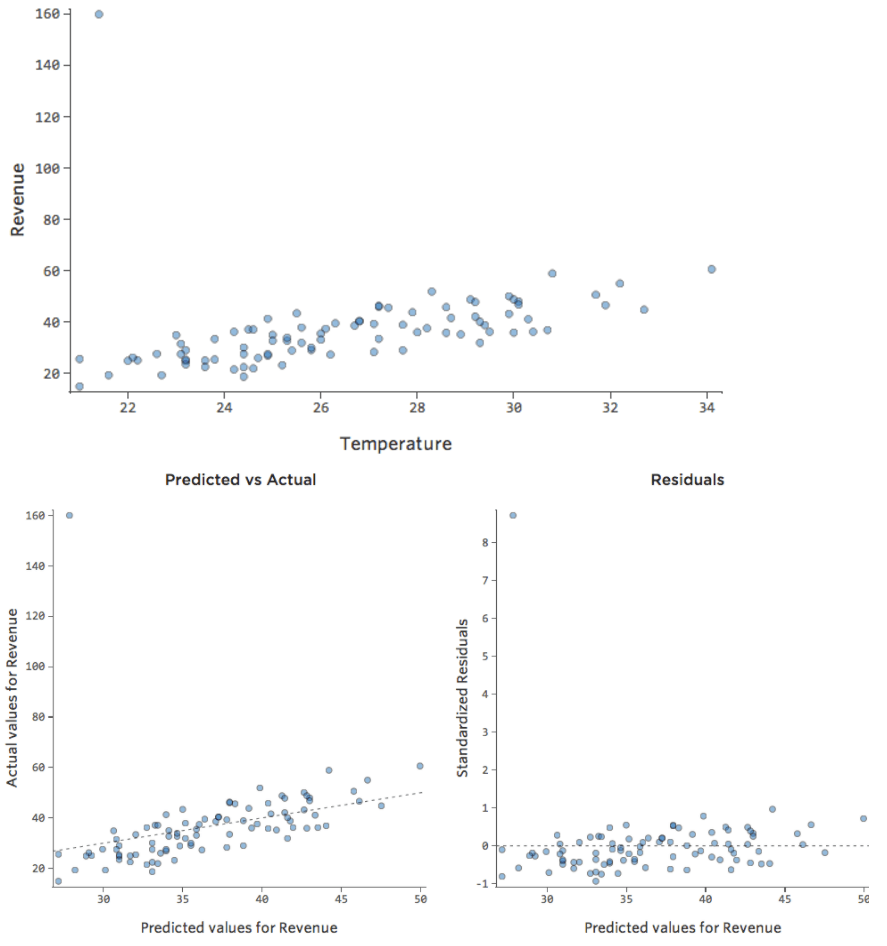
E se uno dei tuoi datapoint avesse un ricavo di 160 dollari invece dei normali 20-60 dollari? I tuoi tracciati apparirebbero nel seguente modo:
Questa regressione ha un datapoint periferico su una variabile di output, “Ricavo”.
Implicazioni
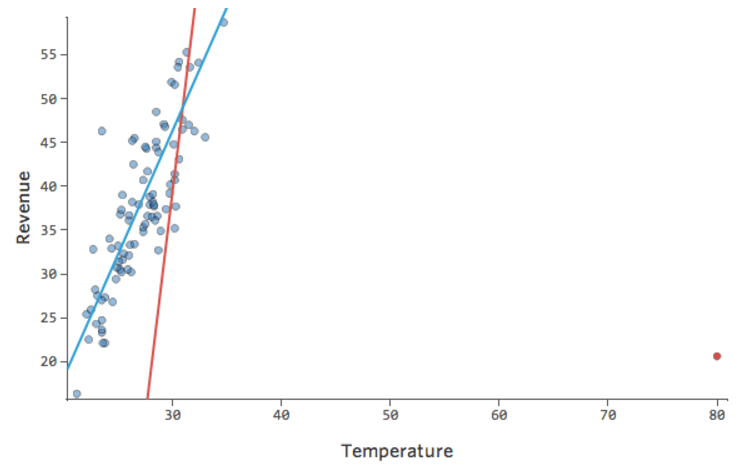
Stats iQ esegue un tipo di regressione che in genere non è influenzato da valori fuori norma di output (come il giorno con un ricavo di 160 dollari), ma è influenzato da valori fuori norma di input (come una “Temperatura” negli 80). Nel peggiore dei casi, il modello può ruotare per cercare di avvicinarsi a quel punto a scapito della vicinanza a tutti gli altri e finire per essere completamente sbagliato, come questo:
La riga blu è probabilmente quello che vorresti fosse il modello, e la linea rossa è il modello che potresti vedere se hai questo valore fuori a “Temperatura” 80.
Come risolvere il problema
- È possibile che si tratti di un errore di misurazione o di inserimento dati, in cui il valore fuori norma è semplicemente errato, nel qual caso è necessario eliminarlo.
- È possibile che ciò che sembra essere solo un paio di valori fuori norma sia in realtà una distribuzione di funzionalità. Prendi in considerazione la trasformazione della variabile se una delle tue variabili ha una distribuzione asimmetrica (ovvero, non è a forma di campana remota).
- Se si tratta effettivamente di un valore fuori norma legittimo, è necessario valutare l’impatto del valore fuori norma.
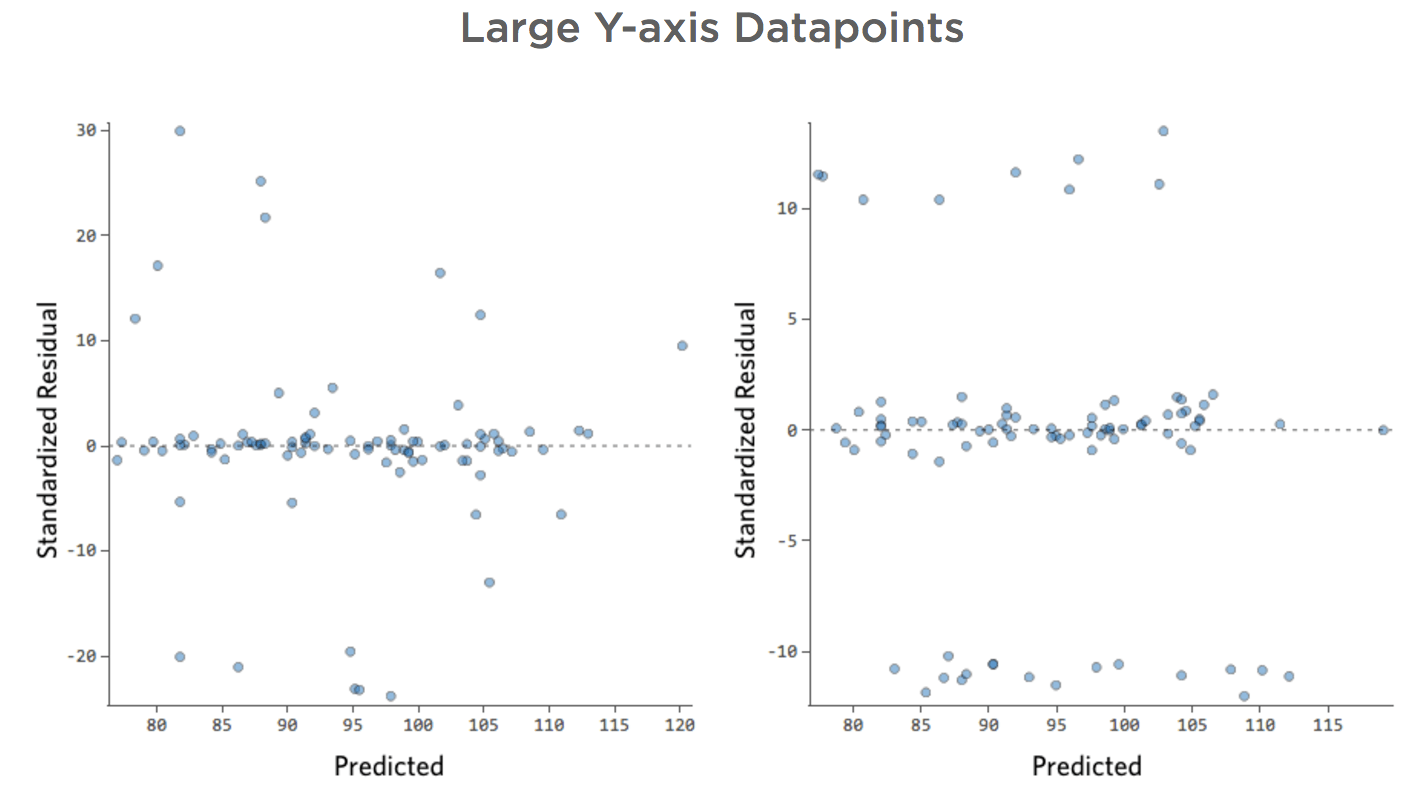
Datapoint dell’asse delle y grandi
- Mostra dettagli su questo tracciato e su come risolverlo.
-
Problema
Immagina che nelle vicinanze ci siano due stand di limonata concorrenti. Nella maggior parte dei casi solo uno è operativo, nel qual caso il ricavo è costantemente buono. Talvolta nessuno dei due è attivo e il ricavo sale; altre volte, entrambi sono attivi e il ricavo precipita.
“Fatturato” rispetto a “Temperatura” potrebbe apparire così…
…con la riga superiore costituita da giorni in cui non si presentano altri stand e la riga inferiore da giorni in cui entrambi gli altri stand sono in attività.
Questo si tradurrebbe in questi tracciati residui:
Questo significa che esistono diversi datapoint su entrambi i lati di 0 che presentano residui pari o maggiori di 10, vale a dire che il modello era molto distante .
Ora, se avessi raccolto dati ogni giorno per una variabile chiamata “Numero di stand di limonata in attività”, potresti aggiungere quella variabile al tuo modello e questo problema sarebbe risolto. Ma spesso non hai i dati di cui hai bisogno (o anche solo un’ipotesi sul tipo di variabile di cui hai bisogno).
Implicazioni
Il modello non è inutile, ma sicuramente non è così efficace come se fossero presenti tutte le variabili necessarie. Potresti comunque usarlo e dire qualcosa di simile: “Questo modello è abbastanza accurato la maggior parte delle volte, ma poi ogni tanto è molto lontano ”. È utile? Probabilmente, ma questa è la tua decisione e dipende dalle decisioni che stai cercando di prendere in base al tuo modello.
Come risolvere il problema
- Anche se questo approccio non funzionerebbe nell’esempio specifico di cui sopra, vale quasi sempre la pena guardarsi intorno per vedere se c’è l’opportunità di trasformare in modo utile una variabile.
- Se però questo non dovesse funzionare, probabilmente dovrai affrontare il tuo problema relativo alla variabile mancante.
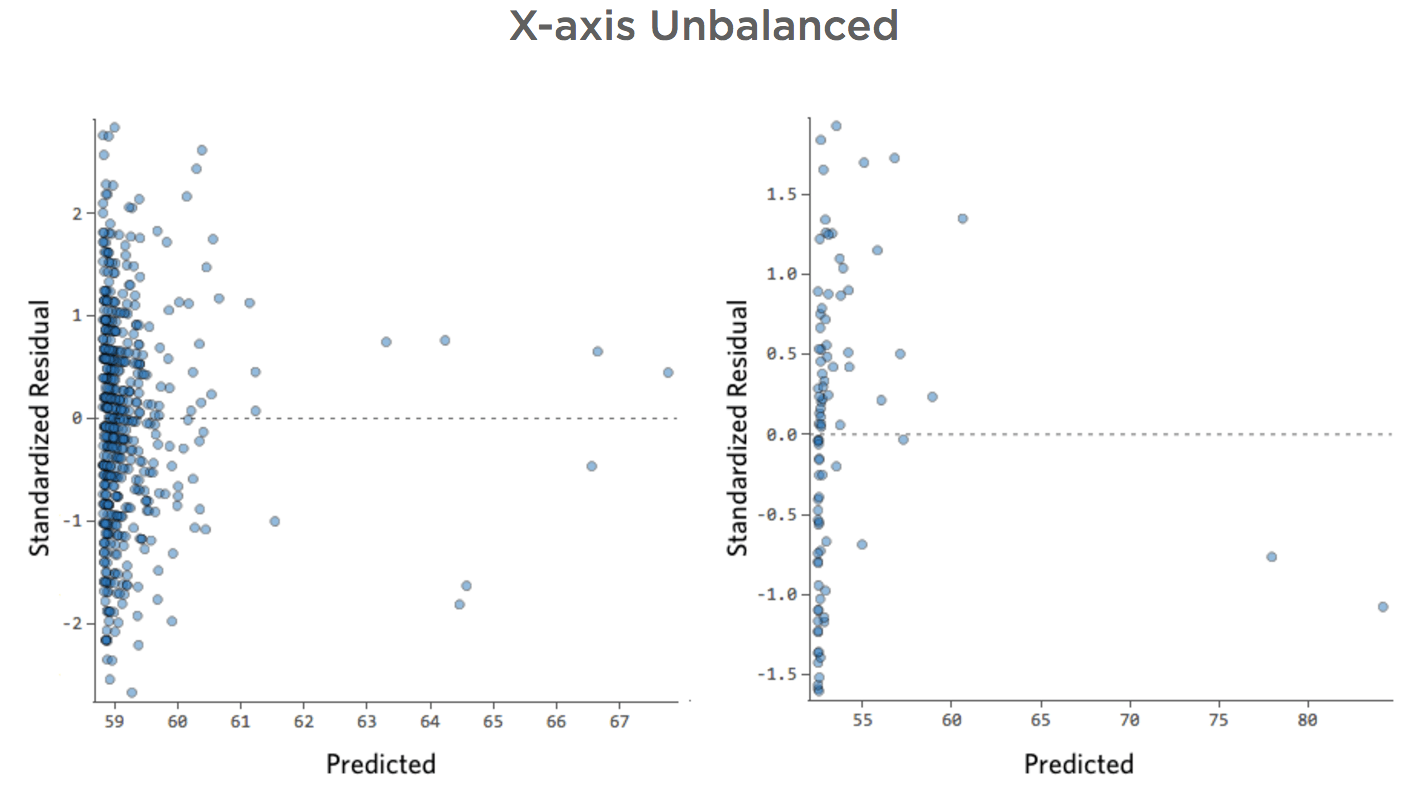
Asse delle x non bilanciato
- Mostra dettagli su questo tracciato e su come risolverlo.
-
Problema
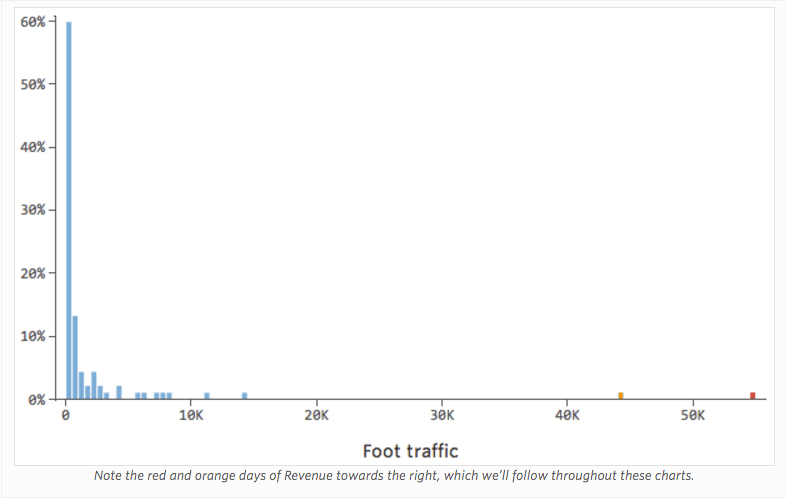
Immagina che “Ricavo” sia guidato dal vicino “Traffico a piedi”, in aggiunta o al posto di “Temperatura”. Immagina che, per qualsiasi motivo, il tuo stand di limonata abbia tipicamente un basso ricavo, ma ogni tanto si hanno giorni di guadagno estremamente alti tali che il tuo ricavo appaia in questo modo…
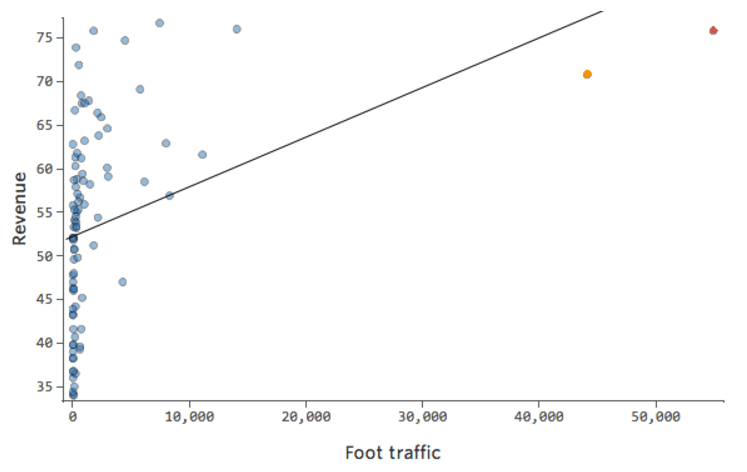
Quindi “Traffico a piedi” rispetto a “Ricavo” potrebbe apparire come segue, con la maggior parte dei dati raggruppati sul lato sinistro:
La linea nera rappresenta l’equazione del modello, la previsione del modello della relazione tra “Traffico di piedi” e “Ricavo”. È possibile osservare che il modello non è in grado di distinguere realmente la differenza tra “Traffico a piedi” di 0 e di, ad esempio, 100 o 1.000; per ciascuno di questi valori prevederebbe un ricavo prossimo a 53 $.
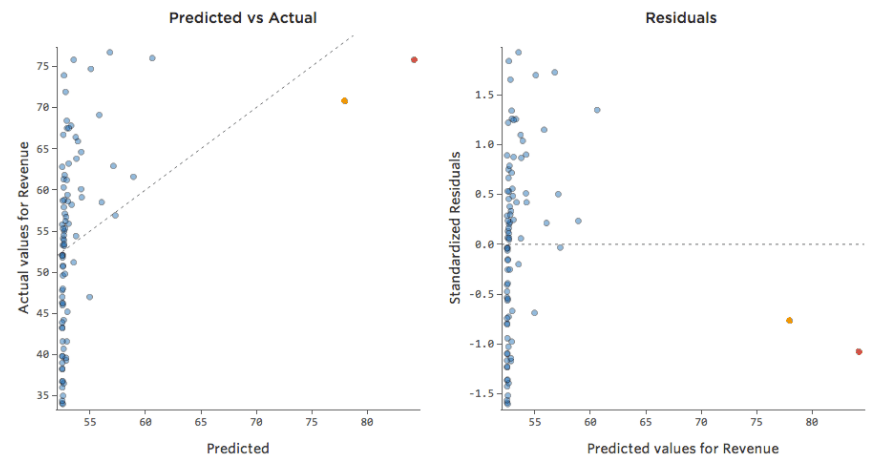
Tradurre gli stessi dati nei tracciati diagnostici:
Implicazioni
Talvolta non c’è nulla di sbagliato nel modello. Nell’esempio precedente, è chiaro che questo non è un buon modello, ma a volte il tracciato residuo non è bilanciato e il modello è piuttosto adeguato.
Gli unici modi per dirlo sono a) sperimentare la trasformazione dei dati e vedere se è possibile migliorarli. e b) guardare al tracciato previsto rispetto a quello reale, e vedere se la previsione è enormemente lontana per molti datapoint, come nell’esempio precedente (ma a differenza dell’esempio seguente).
Sebbene non esista una regola esplicita che dica che il residuo non può essere sbilanciato ed essere comunque accurato (anzi, questo modello è molto accurato), più spesso si dà il caso che un residuo sbilanciato sull’asse delle x indica che il modello può essere reso significativamente più accurato. Nella maggior parte dei casi, si noterà che il modello era direzionalmente corretto ma abbastanza inaccurato rispetto a una versione migliorata. Non è raro risolvere un problema del genere e di conseguenza vedere il salto a R-quadrato del modello da 0,2 a 0,5 (su una scala da 0 a 1).
Come risolvere il problema
- La soluzione è quasi sempre quella di trasformare i dati, in genere una variabile esplicativa. (Tieni presente che l’esempio mostrato qui di seguito farà riferimento alla trasformazione della tua variabile di risposta , ma lo stesso processo sarà utile qui).
- È anche possibile che nel modello manchi una variabile.
Miglioramento del modello: valutazione dell’impatto di un valore fuori norma
Si supponga di avere un datapoint periferico legittimo, non un errore di misurazione o di dati. Per decidere come procedere, è necessario valutare l’impatto del datapoint sulla regressione.
Il modo più semplice per eseguire questa operazione è notare i coefficienti del modello corrente, quindi filtrare quel datapoint dalla regressione. Se il modello non cambia molto, non c’è molto di cui preoccuparsi.
Se questo cambia il modello in modo significativo, esaminalo (in particolare il modello reale rispetto al previsto) e decidi quale si adatta meglio a te. Va bene scartare alla fine il valore fuori purché sia teoricamente possibile difendere questa posizione, dicendo: “In questo caso non siamo interessati ai valori fuori norma, semplicemente non sono di nostro interesse” o “Era il giorno in cui lo zio Jerry è venuto a comprare e mi ha dato una mancia di 100 dollari; questo non è prevedibile, e non vale la pena includerlo nel modello.”
Miglioramento del modello: trasformazione delle variabili
Panoramica
Il modo più comune per migliorare un modello è trasformare una o più variabili, di solito utilizzando una trasformazione “del log”.
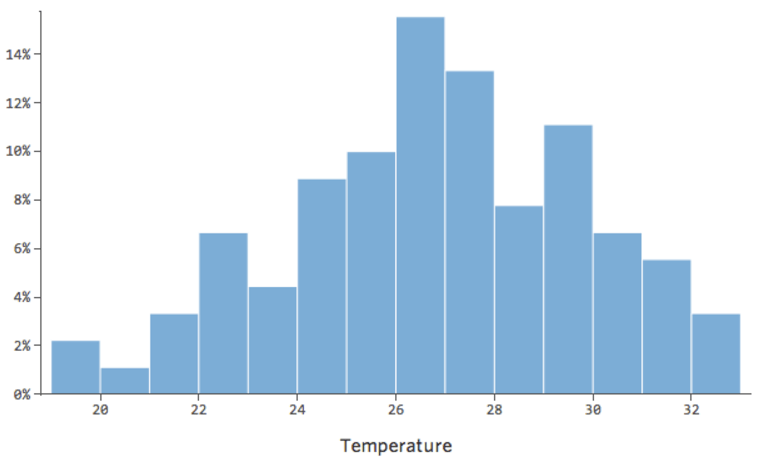
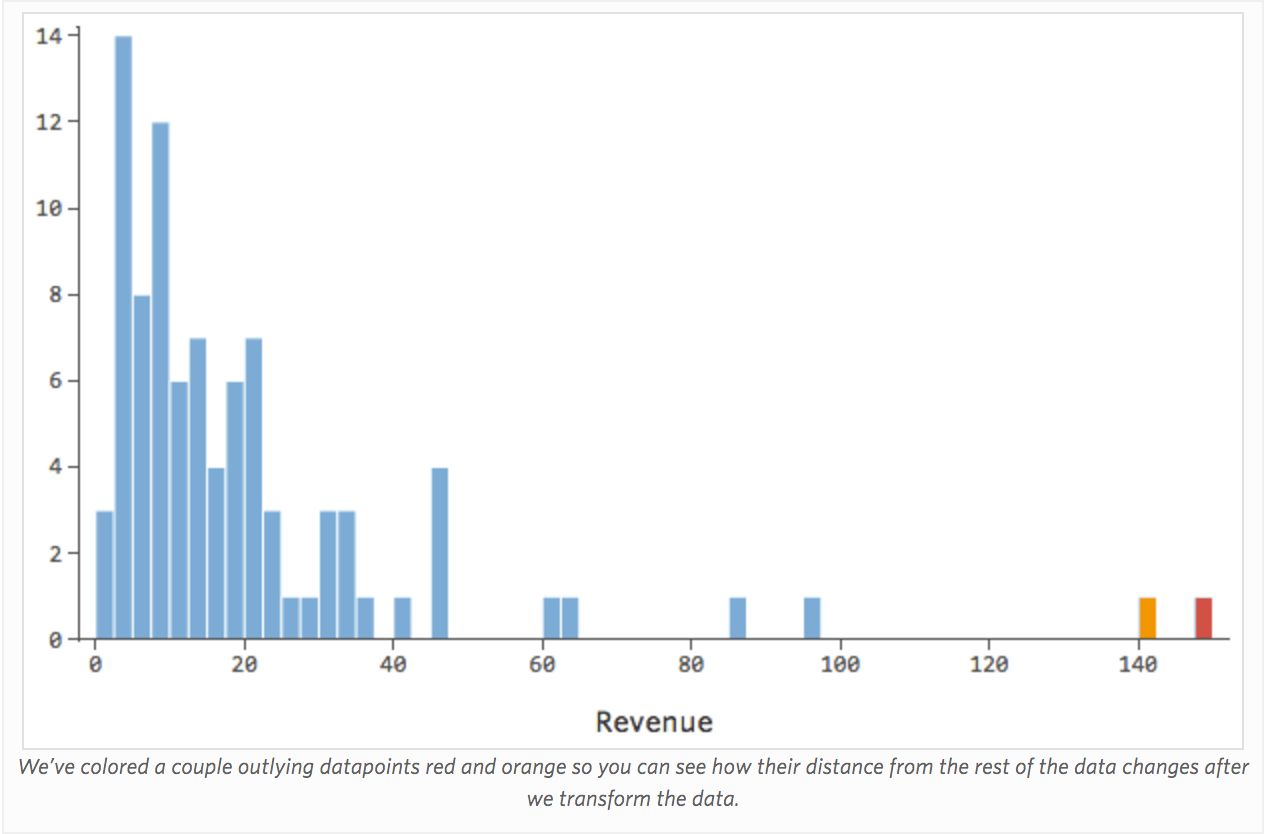
Trasformare una variabile cambia la forma della sua distribuzione. Solitamente il punto migliore per iniziare è una variabile che abbia una distribuzione asimmetrica, al contrario di una distribuzione più simmetrica o a forma di campana. Trova quindi una variabile come questa da trasformare:
In generale, i modelli di regressione funzionano meglio con curve più simmetriche e a forma di campana. Prova diversi tipi di trasformazioni fino a toccare quello più vicino a quella forma. Spesso non è possibile approssimarsi, ma questo è l’obiettivo. Supponiamo quindi di prendere la radice quadrata di “Ricavo” come un tentativo di ottenere una forma più simmetrica, e la tua distribuzione apparirà nel seguente modo:
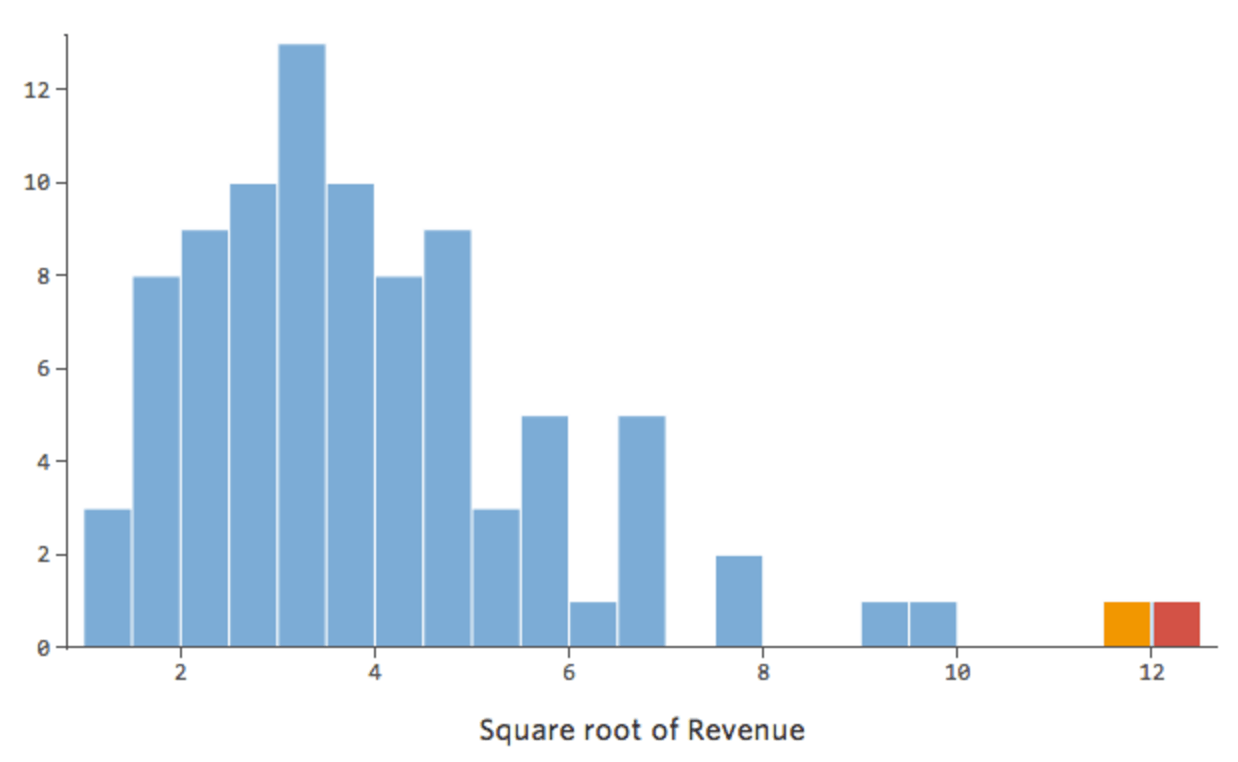
Va bene, ma è ancora un po’ asimmetrico. Proviamo invece a prendere il log di “Ricavo”, che restituisce questa forma:
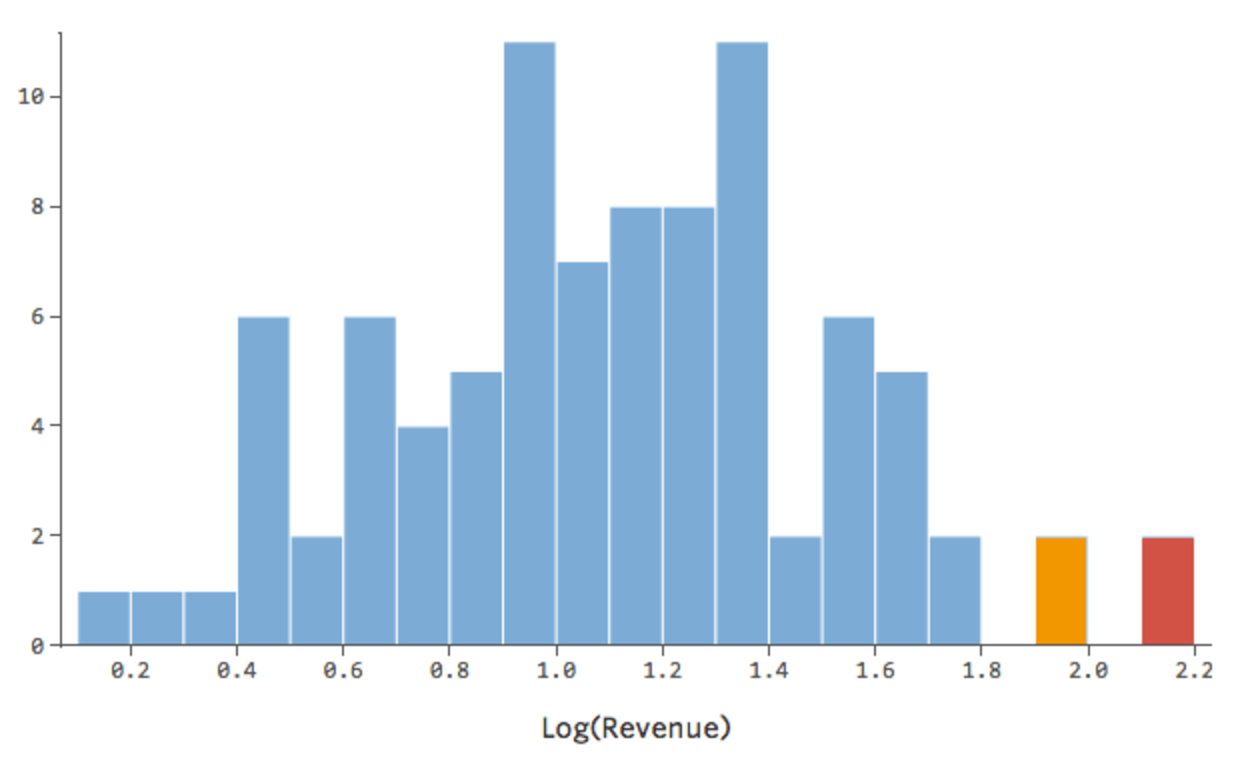
È bello e simmetrico. Probabilmente si otterrà un modello di regressione migliore con log(“Ricavo”) anziché “Ricavo”. In effetti, ecco come potrebbe cambiare la tua equazione, i tuoi residui e il tuo R-quadrato:
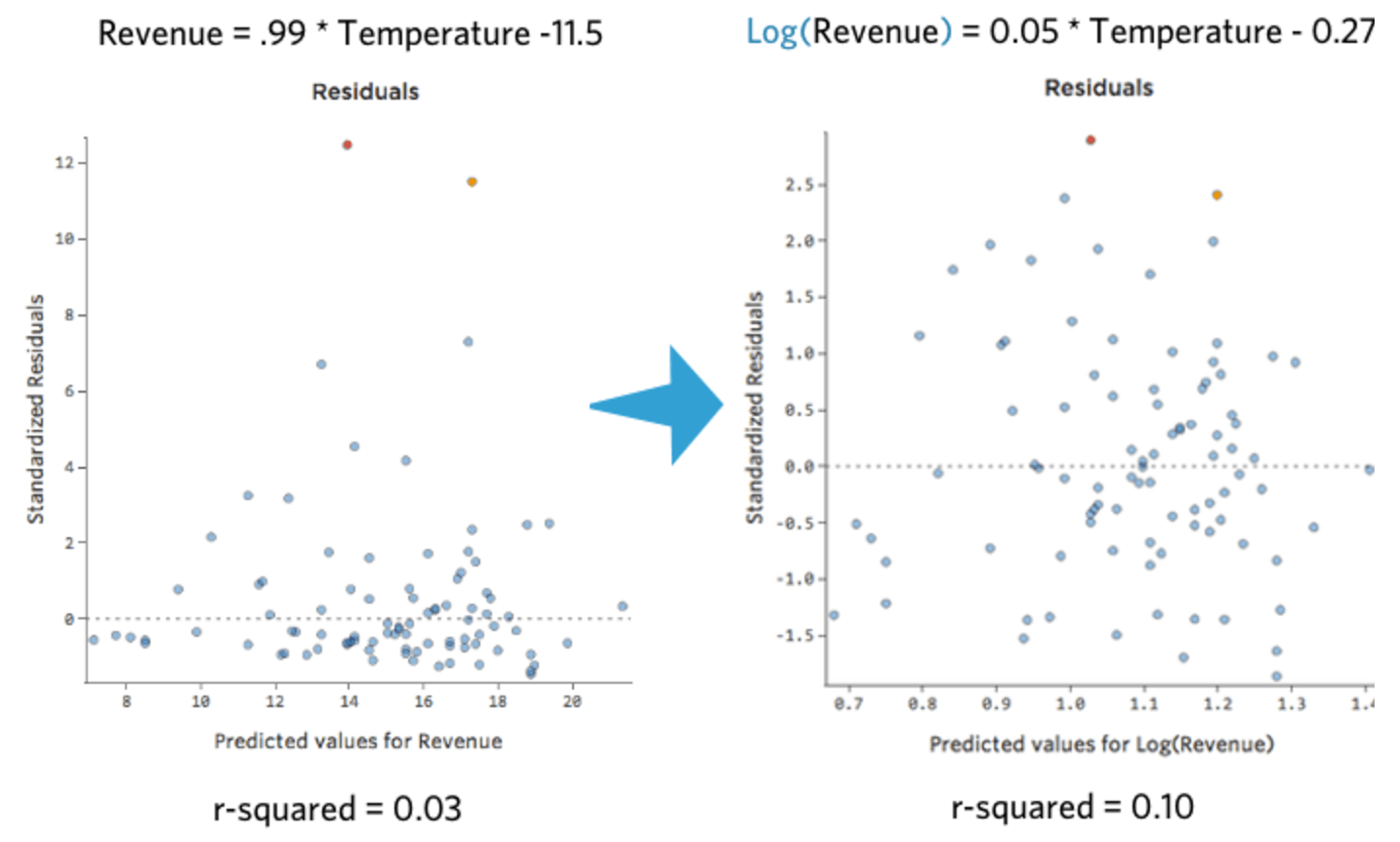
Stats iQ mostra una piccola versione della distribuzione della variabile in linea con l’equazione di regressione: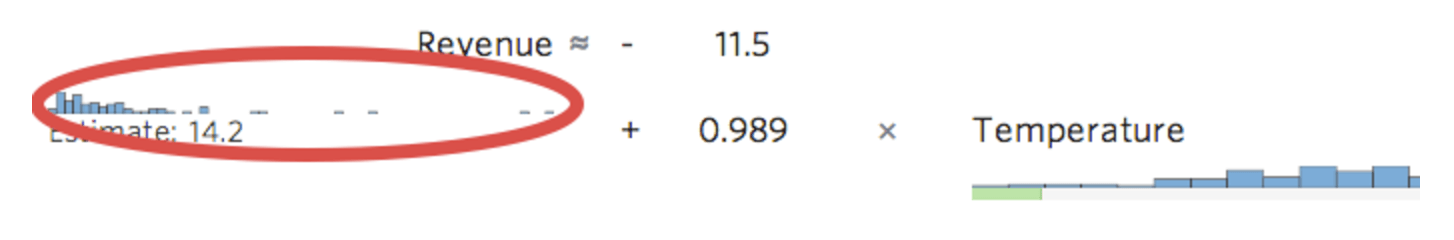
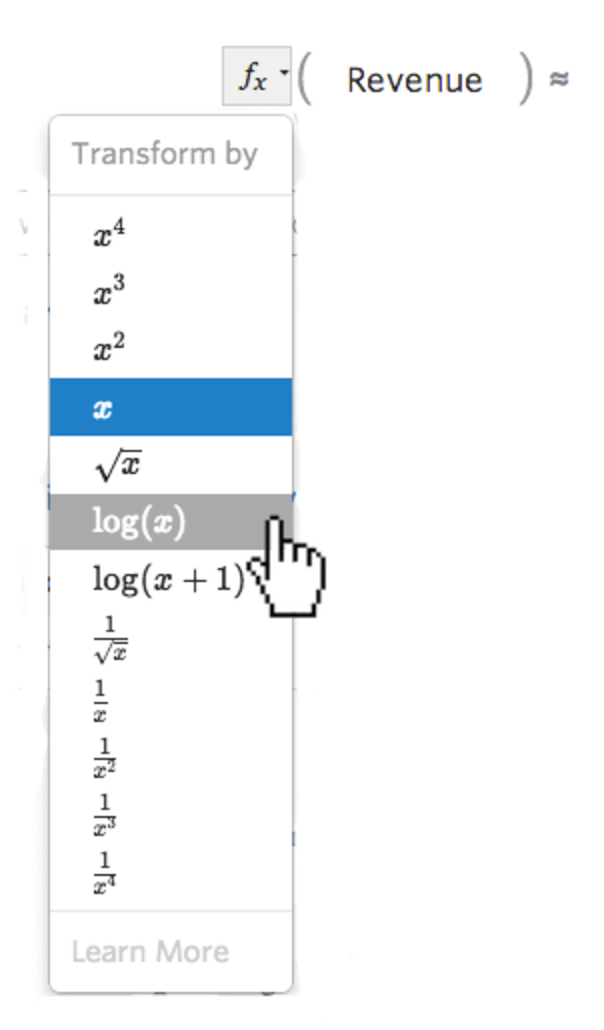
Seleziona il pulsante fx di trasformazione a sinistra della variabile…
…quindi seleziona una trasformazione, molto spesso log(x)...
…quindi esamina l’istogramma per vedere se è più centrato, poiché questo è l’istogramma dopo la trasformazione:

Dopo aver trasformato una variabile, nota come cambia la sua distribuzione, l’R-quadrato della regressione e i modelli del tracciato residuo. Se migliorano (in particolare R-quadrato e i residui), probabilmente è meglio mantenere la trasformazione.
Se è necessaria una trasformazione, è necessario iniziare con una trasformazione “del log” perché i risultati del modello saranno comunque di facile comprensione. Tuttavia, si verificheranno problemi se i dati che si sta tentando di trasformare includono zeri o valori negativi. Per capire perché la lettura di un log è così utile, se si hanno numeri non positivi da trasformare o se si desidera solo comprendere meglio ciò che accade quando si trasformano i dati, leggi i dettagli qui di seguito.
Dettagli
Se prendi il log10() di un numero, stai dicendo “10 a quale potenza mi dà quel numero”. Qui di seguito è riportata, ad esempio, una semplice tabella di quattro datapoint che includono sia “Ricavo” che Log(“Ricavo”):
| Temperatura | Ricavo | Log(Ricavo) |
|---|---|---|
| 20 | 100 | 2 |
| 30 | 1.000 | 3 |
| 40 | 10.000 | 4 |
| 45 | 31.623 | 4,5 |
Se tracciamo “Temperatura” rispetto a “Ricavo” e “Temperatura” rispetto a Log(“Ricavo”), quest’ultimo modello si adatta molto meglio.
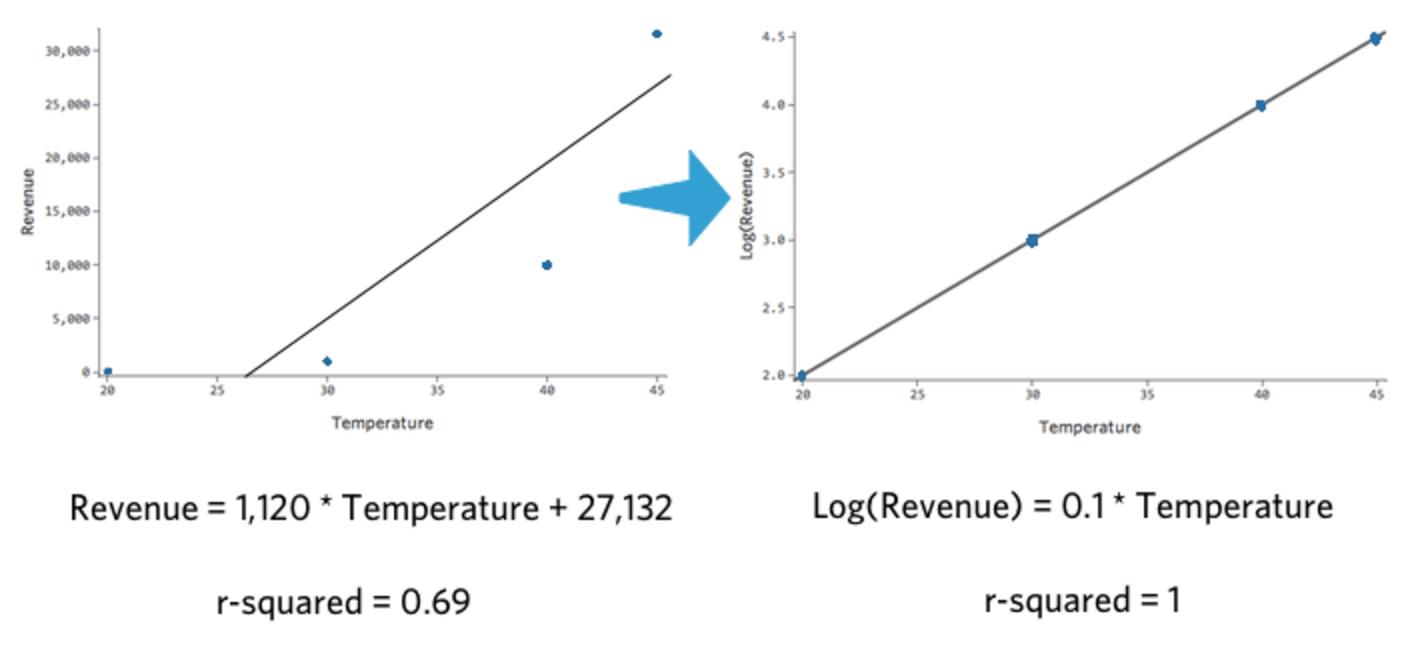
La cosa interessante di questa trasformazione è che la regressione non è più lineare. Quando “Temperatura” è passato da 20 a 30, “Ricavo” è passato da 10 a 100, un gap di 90 unità. Quindi quando “Temperatura” è passato da 30 a 40, “Ricavo” è passato da 100 a 1000, un gap molto più ampio.
Se hai preso un registro della tua variabile di risposta, un aumento di un’unità in “Temperatura” non indica un aumento dell’unità X in “Ricavo”. Ora si tratta di un aumento dell’X–per cento in “Ricavo”. In questo caso un aumento di “Temperatura” di dieci unità è associato ad un aumento del 1000% di Y – ovvero un aumento di una unità di “Temperatura” è associato ad un aumento del 26% di “Ricavo”.
Nota: inoltre, non è possibile prendere il log di 0 o di un numero negativo (non c’è X dove 10X = 0 o 10X= -5), quindi se esegui una trasformazione di log, perderai quei datapoint dalla regressione. Esistono quattro modi comuni di gestire la situazione:
- Prendiamo una radice quadrata o una radice cubica. Queste non cambieranno la forma della curva in modo così drastico come se prendessimo un log, ma consentiranno agli zeri di rimanere nella regressione.
- Se non sono troppe le righe di dati con valore zero e tali righe non sono teoricamente importanti, è possibile decidere di proseguire con il log e perdere alcune righe dalla regressione.
- Invece di prendere log(y), prendi log(y+1), in modo che gli zeri diventino uno e possano poi essere mantenuti nella regressione. Questo provocherà una leggera distorsione e disorientamento del modello, ma nella pratica i suoi effetti negativi sono in genere di minore importanza.
Miglioramento del modello: variabili mancanti
Probabilmente il motivo più comune per cui un modello non riesce ad adattarsi è che non sono incluse tutte le variabili corrette. Questo particolare problema presenta molte soluzioni possibili.
Aggiunta di una nuova variabile
A volte la correzione è semplice come l’aggiunta di un’altra variabile al modello. Ad esempio, se il traffico “Ricavo” dello stand di limonata era molto maggiore nei fine settimana piuttosto che nei giorni feriali, il tracciato previsto rispetto a quello reale potrebbe essere il seguente (R-quadrato di 0,053), poiché il modello sta considerando solo la media di giorni del fine settimana e giorni feriali:
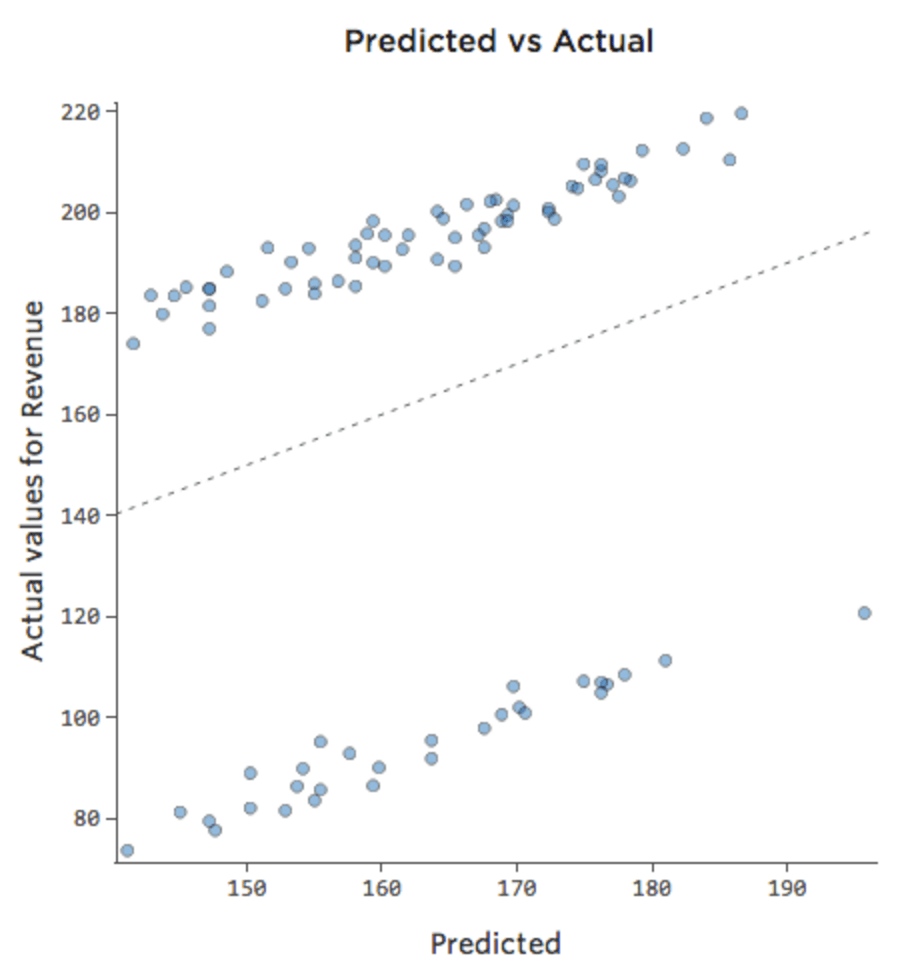
Se il modello include una variabile denominata “Weekend”, il tracciato previsto rispetto a quello reale potrebbe essere il seguente (R-quadrato di 0,974):
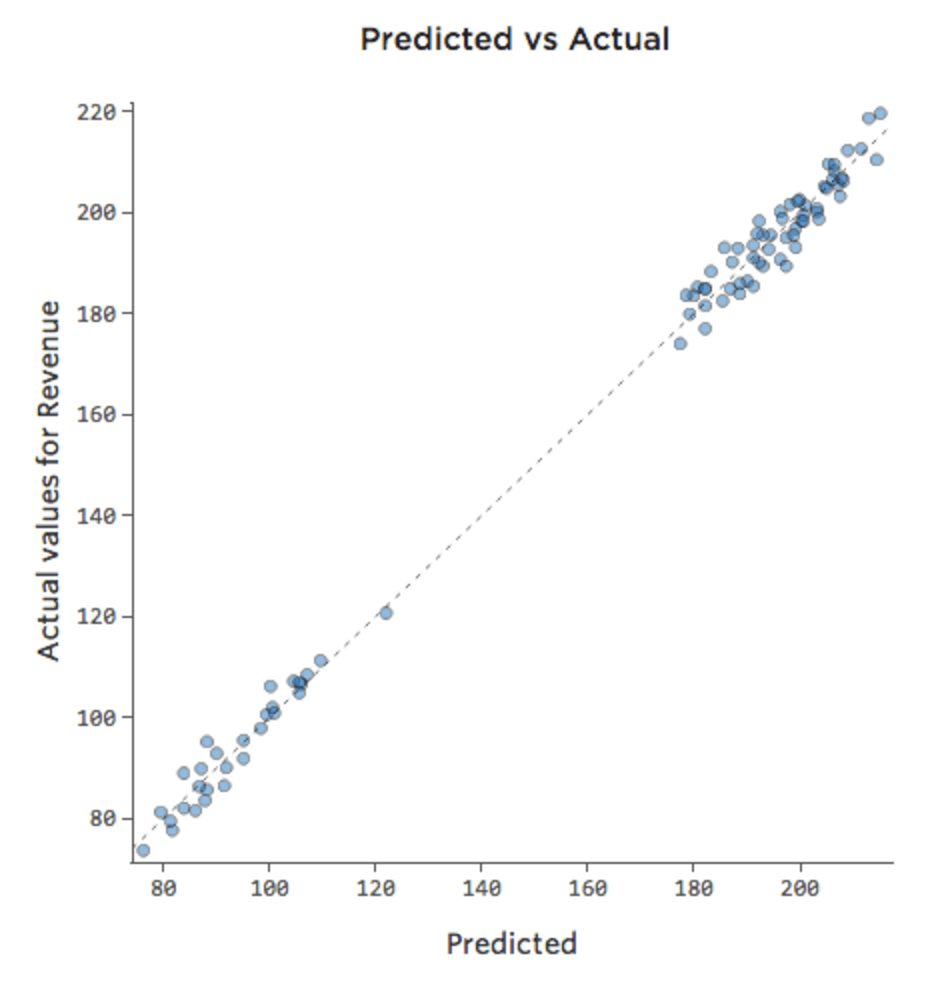
Il modello effettua previsioni molto più accurate perché è in grado di prendere in considerazione se un giorno della settimana è un giorno feriale o meno.
Tieni presente che a volte dovrai creare variabili in Stats iQ per migliorare il tuo modello in questo modo. Ad esempio, si potrebbe avere una variabile “Data” (con valori come “26/10/2014”) e potrebbe essere necessario creare una nuova variabile denominata “Giorno della settimana” (ad esempio, domenica) o Fine settimana (ad esempio, Fine settimana).
Variabile omessa non disponibile
Raramente, però, è così facile. Molto spesso la variabile rilevante non è disponibile perché non si sa cosa sia o perché era difficile da raccogliere. Forse non si tratta di un problema di fine settimana rispetto ai giorni feriali, ma piuttosto di un problema simile al “Numero di concorrenti nell’area” che non è stato possibile raccogliere all’epoca.
Se la variabile necessaria non è disponibile o non si sa nemmeno quale sarebbe, il modello non può essere realmente migliorato e deve essere valutato per decidere quanto è soddisfacente(se è utile o meno, anche se presenta difetti).
Interazioni tra variabili
Forse nei fine settimana lo stand di limonata vende sempre al 100% della capacità, quindi indipendentemente dal fatto che “Temperatura” o “Ricavo” sia alto. Ma nei giorni feriali lo stand di limonata è molto meno trafficato, quindi “Temperatura” è un fattore importante di “Ricavo”. Se è stata eseguita una regressione che includeva “Fine settimana” e “Temperatura”, potrebbe essere visualizzato un tracciato previsto rispetto a quello reale come questo, in cui la riga in cima corrisponde ai giorni del fine settimana.
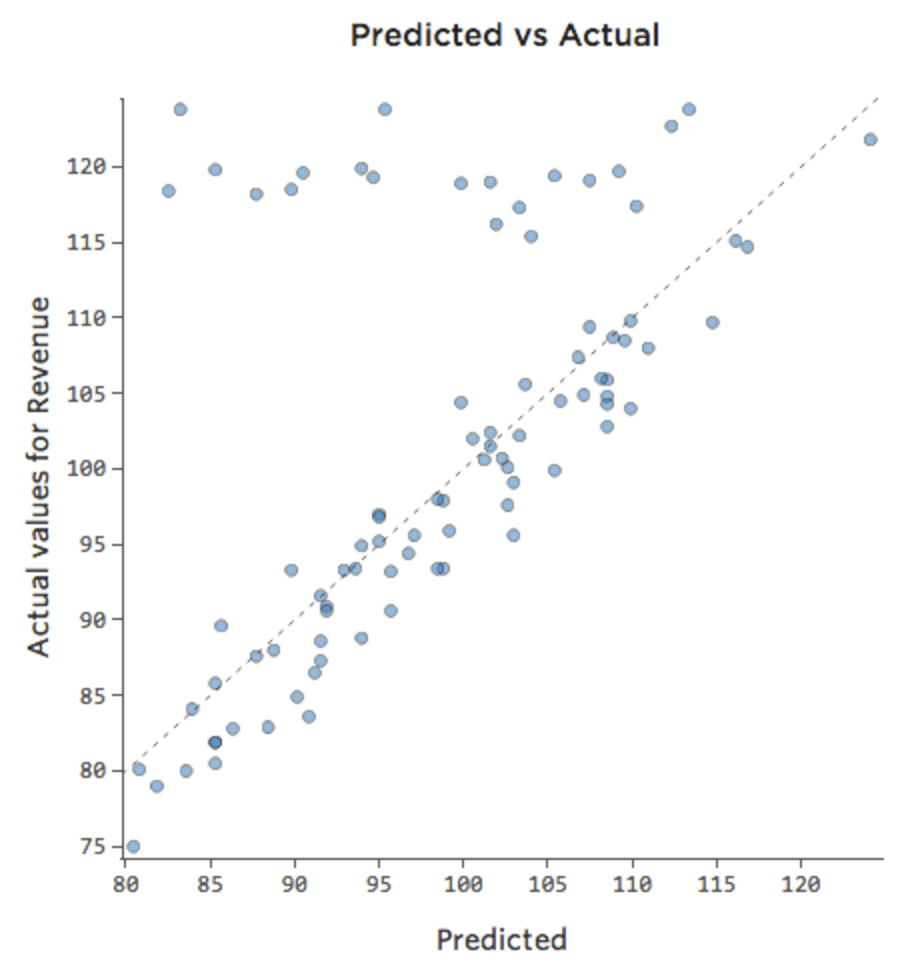
Diremmo che c’è un’interazione tra “Weekend” e “Temperatura”; l’effetto di uno di essi sul “Ricavo” è diverso in base al valore dell’altro. Se si crea una variabile di interazione, si ottiene un modello molto migliore, in cui il confronto tra previsto e reale è il seguente:
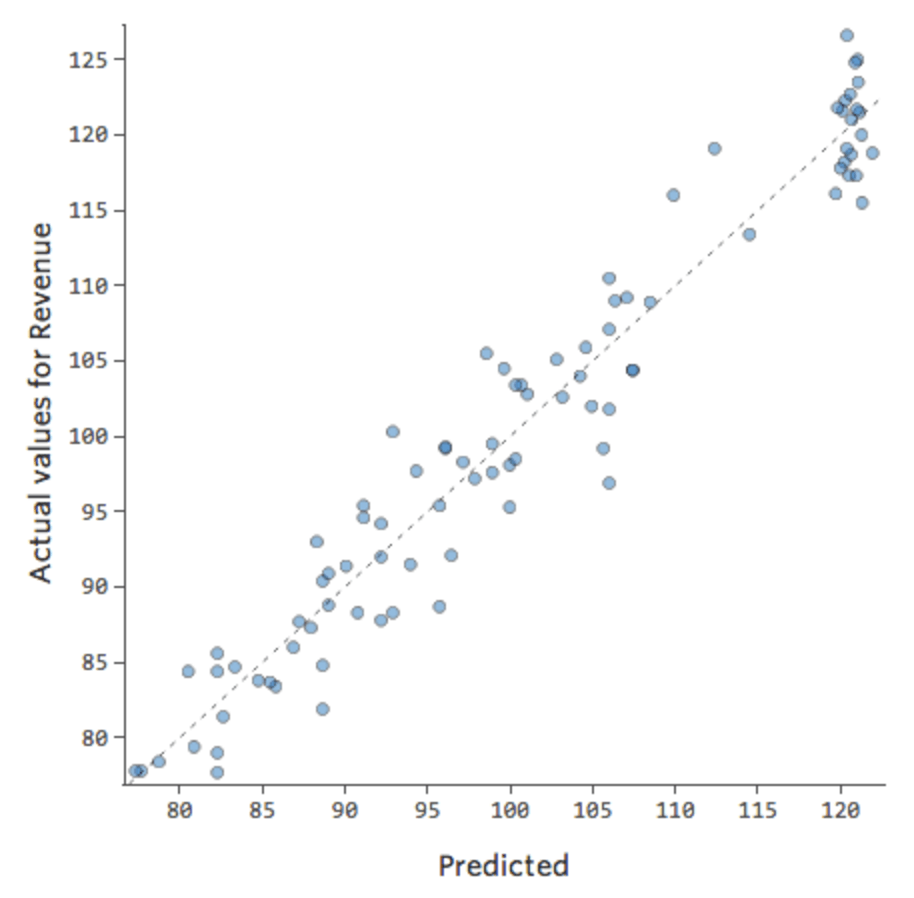
Miglioramento del modello: correzione della non linearità
Si supponga di avere una relazione che ha il seguente aspetto:
Si potrebbe notare che la forma è quella di una parabola, che si potrebbe ricordare è generalmente associata a formule che hanno il seguente aspetto:
y = x2 + x + 1
Per impostazione predefinita, la regressione utilizza un modello lineare simile a questo:
y = x + 1
Infatti, la linea nel tracciato precedente ha questa formula:
y = 1,7x + 51
Ma è un adattamento terribile. Se aggiungiamo quindi un termine x2, il nostro modello ha maggiori possibilità di adattarsi alla curva. In fatti, crea quanto segue:
La formula per tale curva è:
y = -2x2 +111x – 1408
Questo significa che i nostri tracciati diagnostici cambiano da così…
…a così:
Da notare che si tratta di tracciati diagnostici adeguati, anche se i dati appaiono sbilanciati verso destra.
L’approccio di cui sopra può essere esteso ad altri tipi di forme, in particolare a una curva a forma di S, aggiungendo un termine x3. Tuttavia, questo è relativamente raro.
Alcune avvertenze:
- In generale, se si ha un termine x2 a causa di un modello non lineare nei dati, è auspicabile avere un termine plain-old-x non x2 . Potresti scoprire che il tuo modello è perfettamente adeguato senza di esso, ma dovresti sicuramente provare entrambi per iniziare.
- L’equazione di regressione potrebbe essere difficile da comprendere. Per l’equazione lineare all’inizio di questa sezione, per ogni unità aggiuntiva di “Temperatura“, il “Ricavo” è aumentato di 1,7 unità. Quando hai sia x2 che x nell’equazione, non è facile dire “Quando la Temperatura sale di un grado, ecco cosa succede”. A volte per questo motivo è più semplice usare solo un’equazione lineare, supponendo che l’equazione si adatti abbastanza bene.