Tradeoff Matrice confusione e Richiamo di precisione

Matrice di confusione

Supponiamo che si stia pensando di dare un ulteriore cubo di zucchero ai clienti che probabilmente torneranno. Ma ovviamente si vuole evitare di regalare inutilmente cubetti di zucchero, quindi li si dà solo ai clienti che secondo il modello hanno almeno il 30% di probabilità di ritorno.

Se avessi qualche nuovo cliente passeggia…

…è possibile utilizzare il nostro modello di regressione per prevedere la loro probabilità di ritorno…

…e decidere di classificare i clienti con almeno il 30% di probabilità come “Tornerà” e dare loro cubetti di zucchero:

Per capire meglio quanto sia accurato il nostro modello, tuttavia, è possibile applicare il modello ai punti di dati già in tuo possesso, dove sai già se quel cliente alla fine ha restituito…

…e valuta l’accuratezza dei dati…

…e poi suddividerle ulteriormente nelle seguenti categorie:

• Vero positivo: Classificato dal modello come “Tornerà” e aveva infatti “Restituito” nella realtà.
• Falso positivo: classificato dal modello come “Tornerà” ma in realtà “Non è tornato” nella realtà.
• Vero negativo: classificato dal modello come “Won’t return” e in realtà “Didn’t return”.
• False Negative: Classificato dal modello come “Won’t return” ma in realtà era “Ritornato” nella realtà.

Infine, è possibile riepilogare tutto questo lavoro in precisione e richiamo.

Precisione:

• Di quelli classificati come “Ritorneranno”, che proporzione effettivamente ha fatto?
• Vero positivo / (vero positivo + falso positivo)

Richiamo:

• Richiamo: di quelli che di fatto “sono tornati”, quale proporzione è stata classificata in quel modo?
• Vero positivo / (vero positivo + falso negativo)

I modelli migliori hanno valori più elevati per precisione e richiamo.

• Si può immaginare un modello con una precisione del 94% (quasi tutti identificati come “Tornerà” fa in realtà) e il 97% di richiamo (quasi tutti coloro che “Restituiti” sono stati identificati come tali).
• Un modello più debole potrebbe avere una precisione del 95% ma un richiamo del 50% (quando identifica qualcuno come “Tornerà”, è in gran parte corretto, ma è erroneamente etichettato come “Non ha restituito” la metà di coloro che in realtà hanno fatto “Ritorno”).
• O forse il modello ha una precisione del 60% e un richiamo del 60%.

Questi numeri dovrebbero fornire un buon senso per quanto sia accurato il modello, anche se in realtà non si desidera mai fare previsioni.

Precisione vs. Curva di richiamo in fabbrica

All’interno di un qualsiasi modello, è anche possibile decidere di enfatizzare la precisione o il richiamo. Magari sei molto a corto di cubetti di zucchero e vuoi solo darli alle persone che hai molta fiducia torneranno, quindi decidi di regalarli solo ai clienti che hanno il 60% di probabilità di ritorno (invece del 30%).

La nostra precisione salirà perché distribuirete dei cubetti di zucchero solo quando sarete davvero sicuri che qualcuno “tornerà”. Il nostro richiamo verrà meno perché ci saranno molte persone che alla fine “Ritornano” a cui non eri abbastanza sicuro da dare un cubo di zucchero.

Precisione:   62%   —>   80%
Richiamo:        60%   —>   30%

Oppure, se ti senti ricco di cubetti di zucchero, potresti darli a chiunque abbia almeno il 10% di possibilità di essere un rimpatriatore.

Precisione:   62%   —>   40%
Richiamo:        60%   —>   90%

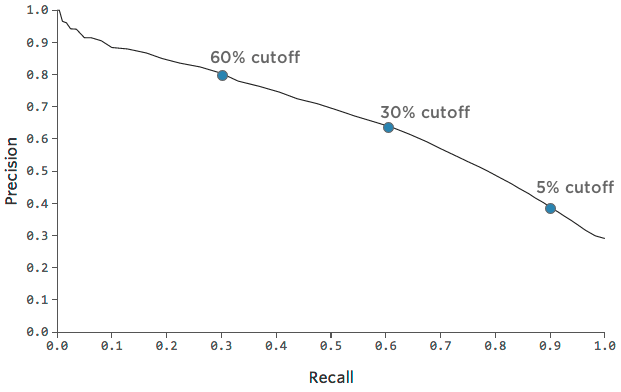
È possibile tracciare questo compromesso tra precisione e richiamo con questo grafico:

Può essere utile selezionare un punto del grafico che rappresenti un bel mix di precisione e richiamo, per poi avere un’idea dell’accuratezza del modello in quel punto.

FAQ