Modello di articolo

Informazioni sulla regressione e sull’importanza relativa

La regressione mostra l’impatto di più variabili di input su una variabile di output. Ad esempio, se entrambi gli input “Anni da cliente” e “Dimensioni dell’azienda” sono correlati con l’output “Soddisfazione” e tra loro, si potrebbe usare la regressione per capire quale dei due input è più importante per creare “Soddisfazione”L’

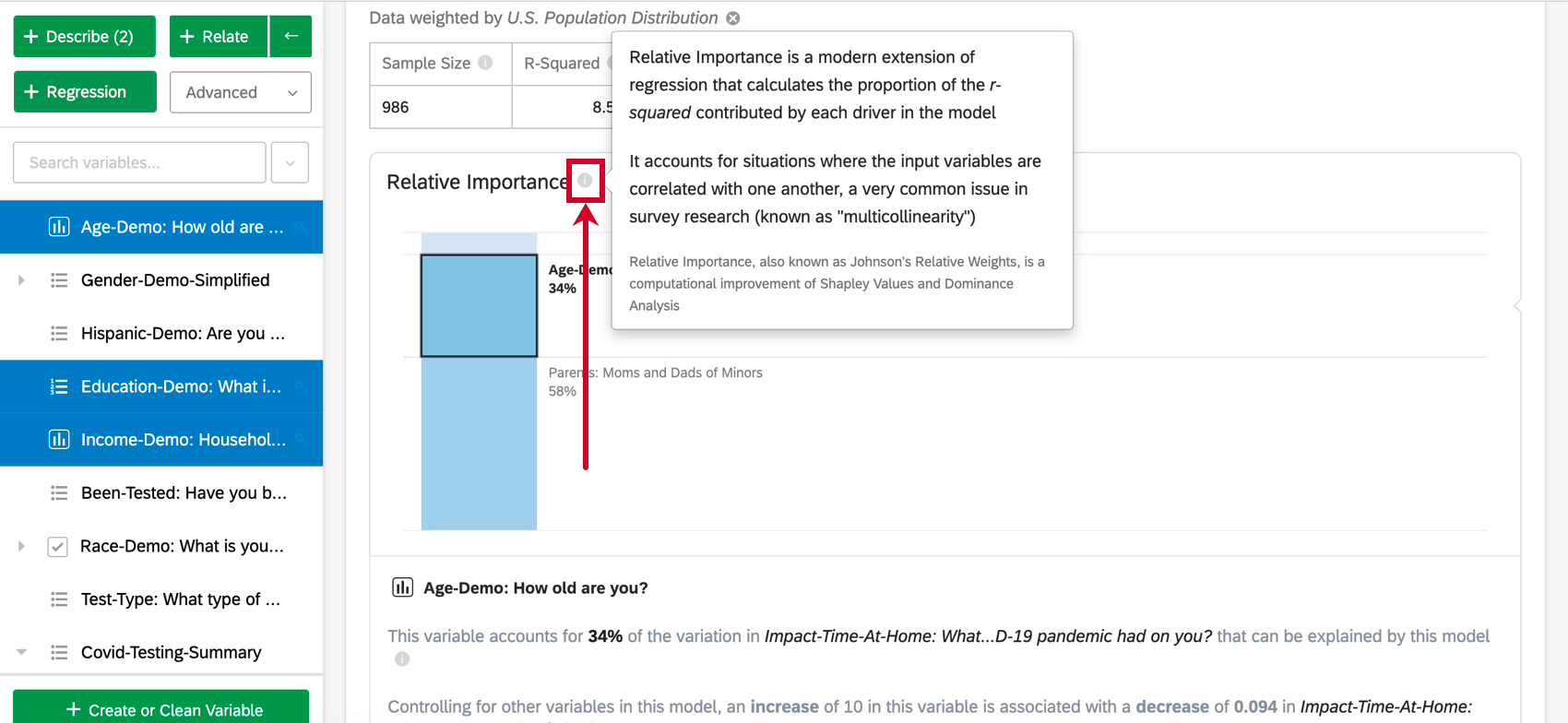
analisi dell’importanza relativa è il metodo migliore per la regressione sui dati di sondaggio e l’output predefinito delle regressioni eseguite in Stats iQ. L’importanza relativa è un’estensione moderna della regressione che tiene conto delle situazioni in cui le variabili di input sono correlate tra loro, un problema molto comune nei sondaggi (noto come “multicollinearità”). L’importanza relativa è nota anche come ponderazione di Johnson, è una variante dell’analisi di Shapley ed è strettamente correlata all’analisi della dominanza.

Di seguito sono riportate le istruzioni su come impostare una regressione in Stats iq. Per ulteriori indicazioni sulla riflessione sulle parti analitiche dell’analisi di regressione, consultare le pagine seguenti:

• Guida di facile consultazione alla regressione lineare
• Interpretare i grafici dei residui per migliorare la regressione lineare
• Guida di facile consultazione alla regressione logistica
• La Matrice di Confusione e il compromesso precisione-richiamo nella Regressione Logistica

Consiglio Q: nella piattaforma Stats iQ sono ora presenti utili tooltip! Mentre si lavora in Stats iQ, è possibile fare clic sulle icone i che appaiono in tutta la piattaforma per visualizzare ulteriori informazioni e definizioni.

Per la regressione lineare, Relative Importance in Stats iQ segue le tecniche descritte in Lipovetsky, Stan & Conklin, Michael. (2001). Analisi della regressione nell’approccio della teoria dei giochi. Modelli stocastici applicati alle imprese e all’industria. 17. 319 – 330. 10.1002/asmb.446.

Selezione delle variabili per le schede di regressione

La creazione di una scheda di regressione consente di capire come il valore di una variabile del set di dati sia influenzato dai valori di altre.

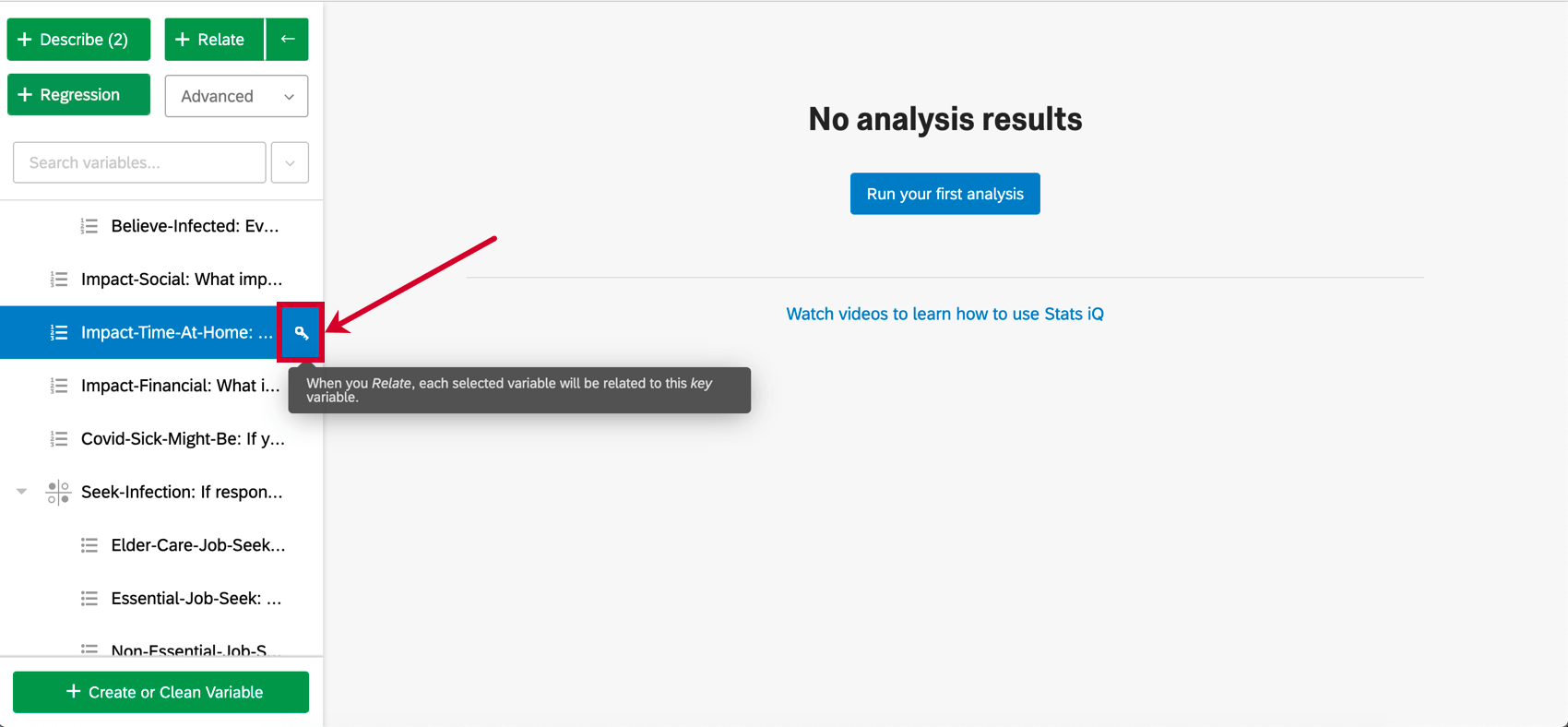
Quando si selezionano le variabili, una variabile avrà una chiave accanto. Per la regressione, la variabile chiave sarà la variabile di uscita. Ogni altra variabile selezionata dopo la variabile chiave sarà una variabile di ingresso. In altre parole, stiamo cercando di spiegare come il valore della variabile di uscita sia determinato dalle variabili di ingresso.

Elementi da considerare quando si selezionano le variabili per la regressione:

• È possibile modificare la variabile chiave facendo clic sull’icona della chiave accanto a qualsiasi variabile nel riquadro delle variabili.
• Se vengono selezionate più variabili rispetto al numero di risposte disponibili, la regressione non verrà eseguita.
• È possibile selezionare fino a 25 variabili di ingresso. Tuttavia, si dovrebbe cercare di selezionare 1-10 variabili di input, altrimenti i risultati potrebbero essere molto complicati.

Se si dispone di un gran numero di variabili da includere in un’analisi, si possono prendere in considerazione i seguenti approcci:

• Eseguire alcune regressioni iniziali ed escludere le variabili che hanno poca importanza nel modello.
• Combinare diverse variabili, ad esempio facendo la media.
• Se la struttura dei dati lo consente, si può utilizzare un processo di importanza relativa in due fasi, come descritto a pagina 341.

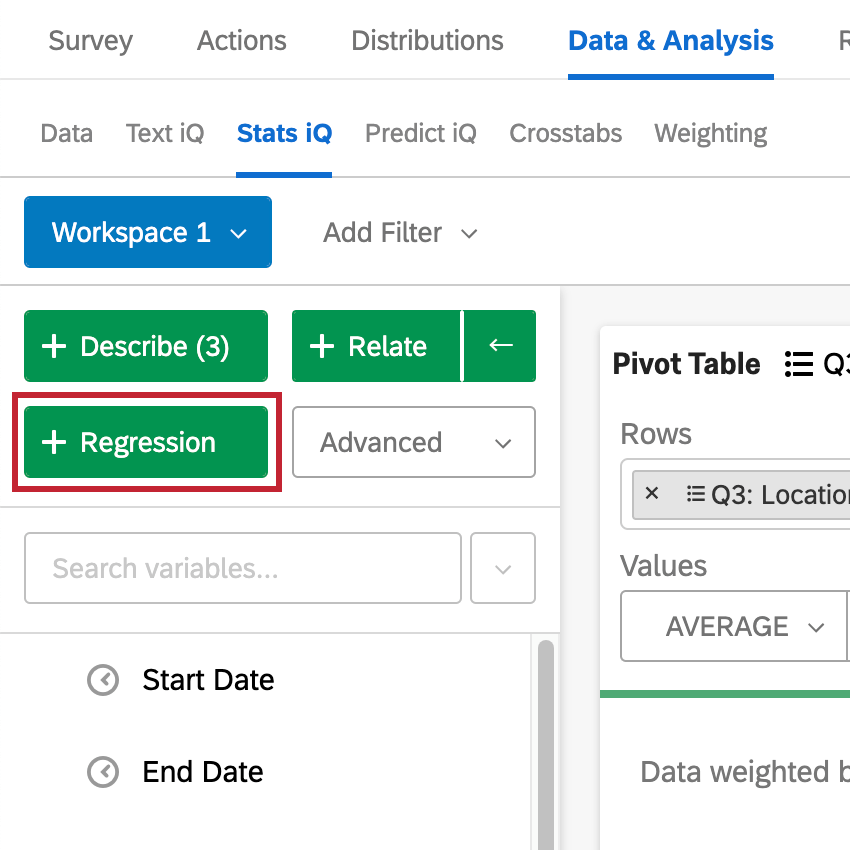
Una volta selezionate le variabili, fare clic su Regressione per eseguire una regressione.

Tipi di regressione

Esistono due tipi principali di regressione in Stats iQ. Se la variabile di output è una variabile numerica, Stats iQ esegue una regressione lineare. Se la variabile di output è una variabile di categoria, Stats iQ esegue una regressione logistica.

In particolare, i tipi di regressione che Stats iQ eseguirà sono i seguenti:

Regressione lineare

L’importanza relativa è combinata con i minimi quadrati ordinari (OLS). L’output deriva dalla combinazione delle due analisi:

• Importanza relativa: Tutto ciò che è riportato in questa sezione proviene dall’Importanza Relativa, tranne l’r-quadrato, che proviene dalla regressione OLS.
• Esplorare il modello in dettaglio: Tutto ciò che è presente in questa sezione proviene da Importanza relativa, tranne le distribuzioni, che sono tratte dai dati stessi.
• Analizzare la diagnostica e i residui della regressione OLS per migliorare il modello: Tutto ciò che viene presentato in questa sezione deriva dalla regressione OLS.

Regressione logistica

La regressione logistica è un metodo di classificazione binaria utilizzato per comprendere i fattori che determinano un risultato binario (ad esempio, sì o no) dato un insieme di variabili di input. Se si esegue una regressione su una variabile di output con più di due gruppi, Stats iQ selezionerà un gruppo e raggrupperà gli altri in modo da renderla una regressione binaria (è possibile modificare il gruppo analizzato dopo l’esecuzione della regressione).

Importanza relativa

Le variabili di input nei dati di sondaggio sono spesso altamente correlate tra loro; si tratta di un problema chiamato “multicollinearità” Questo può portare a risultati di regressione che aumentano artificialmente l’importanza di una variabile e diminuiscono quella di un’altra variabile correlata. L’importanza relativa è riconosciuta come il metodo migliore per tenerne conto.

L’importanza relativa (in particolare le Ponderazioni relative di Johnson) non soffre di questo problema e bilancia adeguatamente l’importanza delle variabili di input, indipendentemente dal tipo di regressione in corso. Inoltre, calcola la ponderazione relativa (o importanza relativa) di ciascuna variabile, ovvero la percentuale di variazione spiegabile nell’output dovuta a quella variabile. Questo viene mostrato come una serie di percentuali che si sommano al 100%.

I risultati sono simili all’esecuzione di una serie di regressioni, una per ogni variazione delle variabili di input. Ad esempio, se si dispone di due variabili, il programma eseguirà l’equivalente di tre regressioni: una con la variabile A, una con la variabile B e una con entrambe. Ciò consente di quantificare l’importanza di ciascuna variabile e di applicare tale quantificazione al risultato della regressione.

Uscita di regressione

Quando si esegue una regressione in Stats iQ, i risultati dell’analisi contengono le seguenti sezioni:

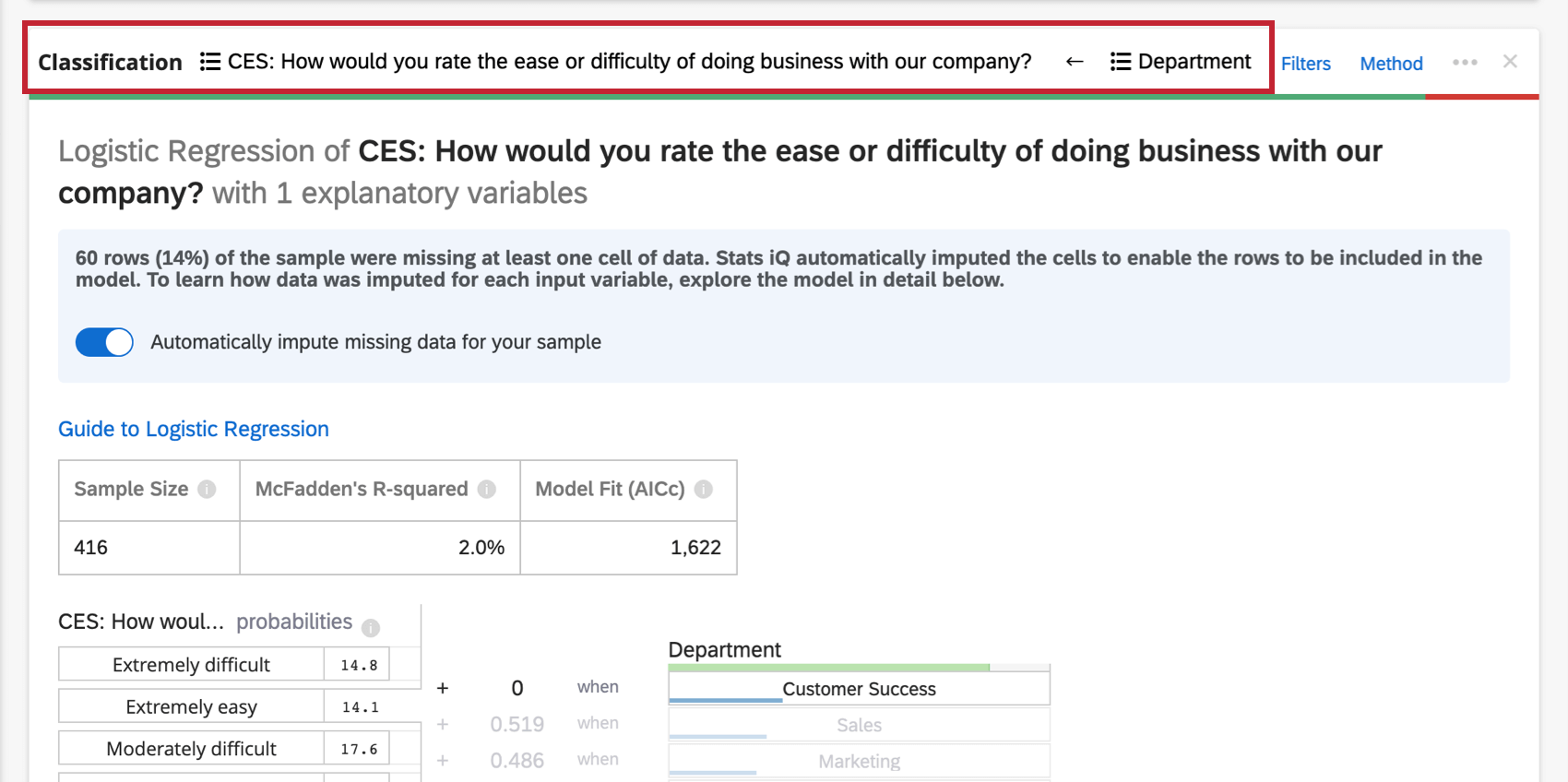
Riepilogo numerico

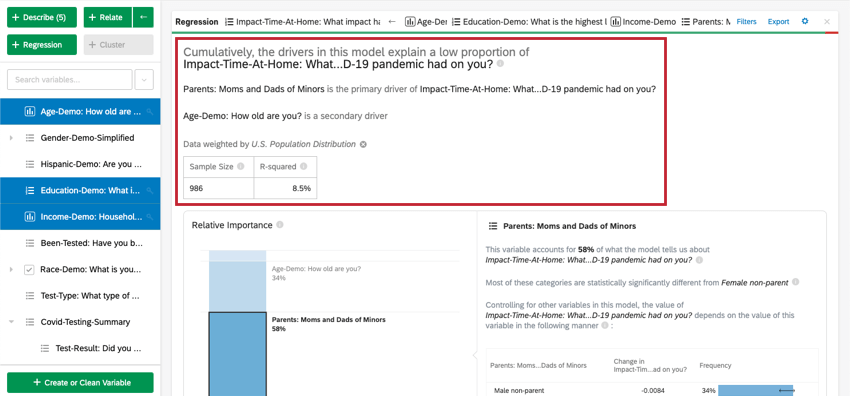
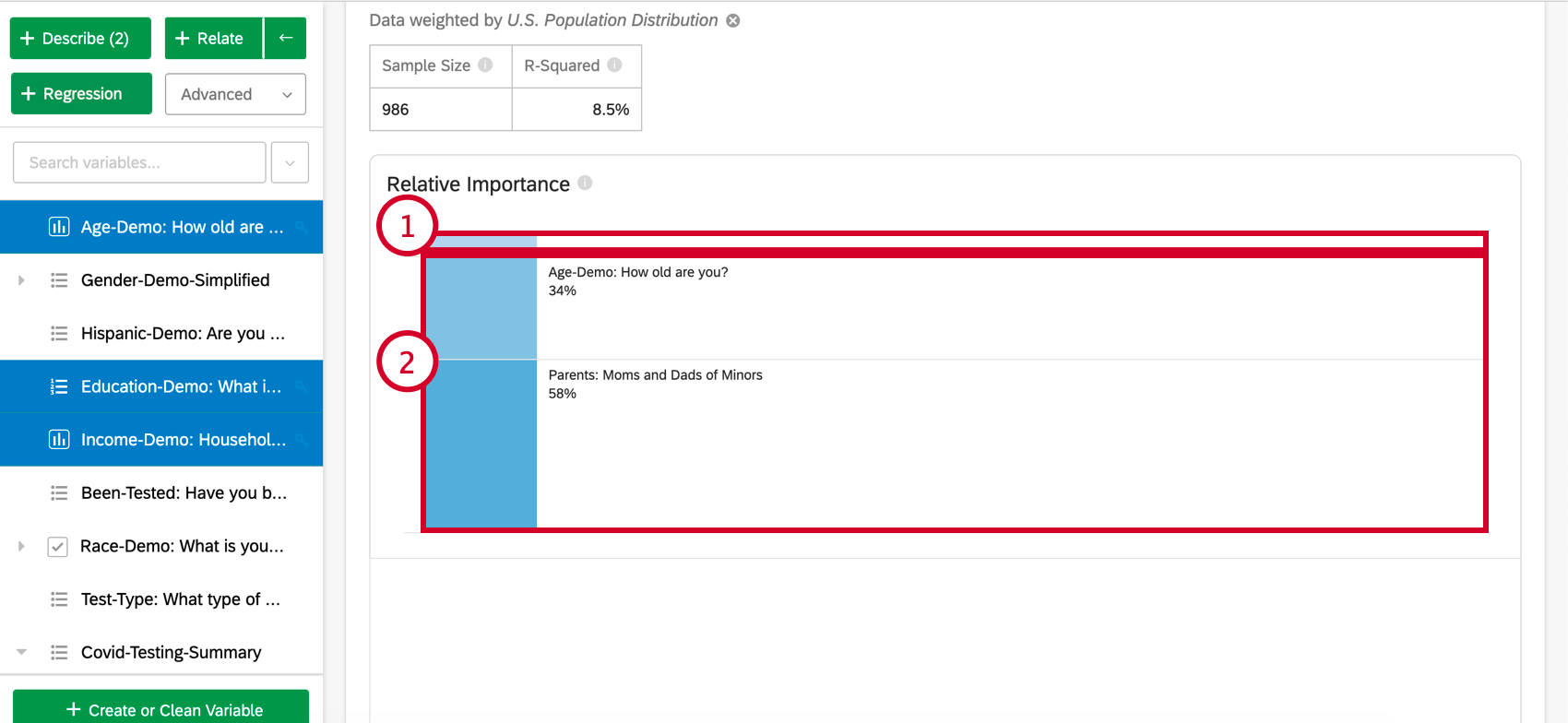
Nella parte superiore della scheda è presente un riepilogo dell’analisi di regressione. Prendendo in esame le variabili scelte, questo riassunto scritto spiega quali variabili sono i driver primari e secondari, nonché i driver che hanno avuto un basso impatto cumulativo. La tabella dati include la dimensione del campione e il valore R-quadrato.

Importanza relativa

1. Variabili a basso impatto: Le variabili che singolarmente hanno un’importanza relativa pari o inferiore al 10% saranno raggruppate insieme. Quando viene selezionata, è presente una sezione che spiega l’importanza relativa e la significatività statistica di ciascuna variabile a basso impatto.
2. Variabili ad alto impatto: Ogni variabile ad alto impatto sarà separata e cliccabile. Una volta selezionata una variabile, sotto il grafico a barre è possibile visualizzare la variazione di cui si è tenuto conto e cosa accadrebbe se altre variabili fossero controllate nel modello.

Ulteriori dettagli sul modello

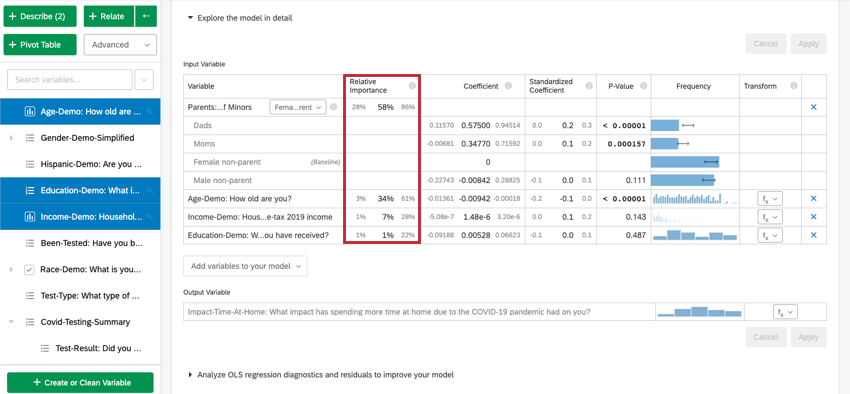
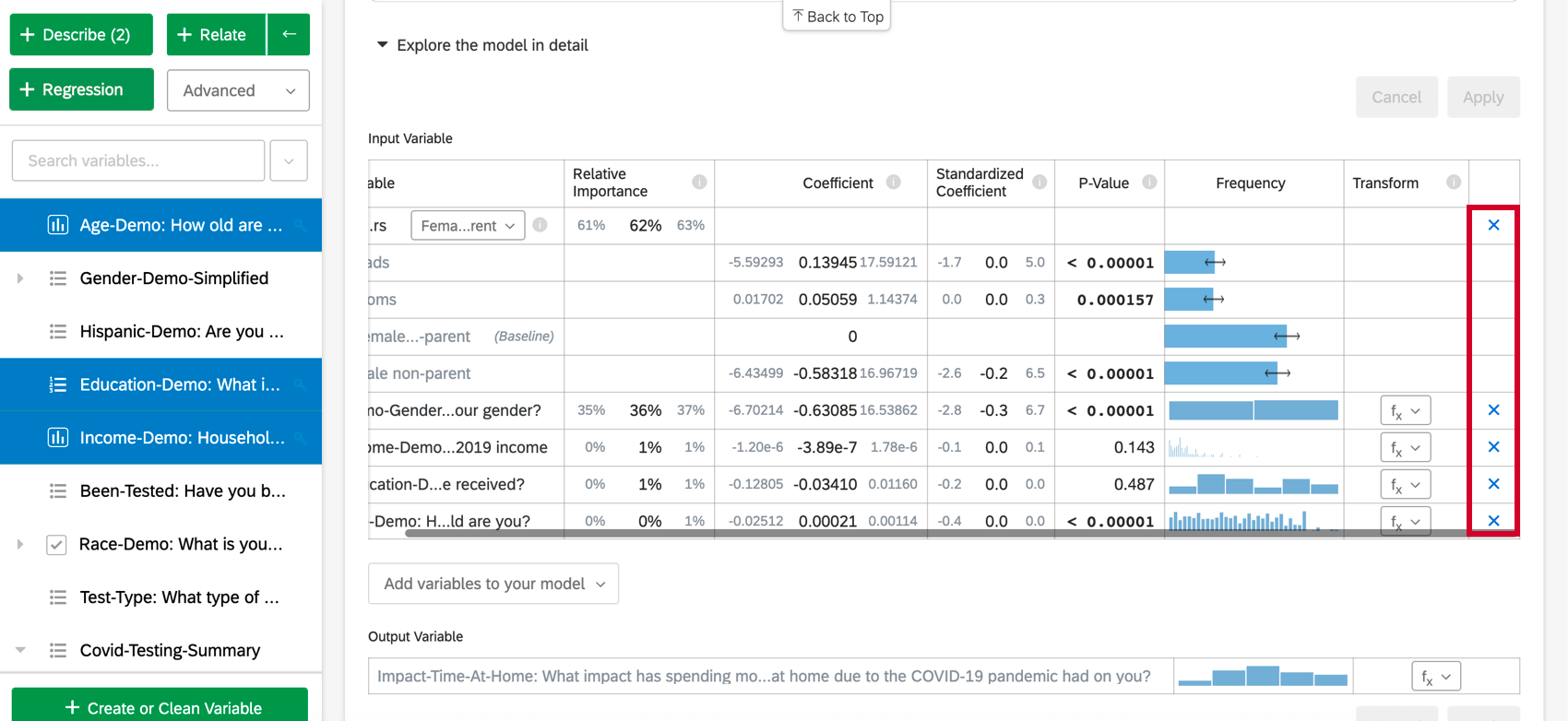
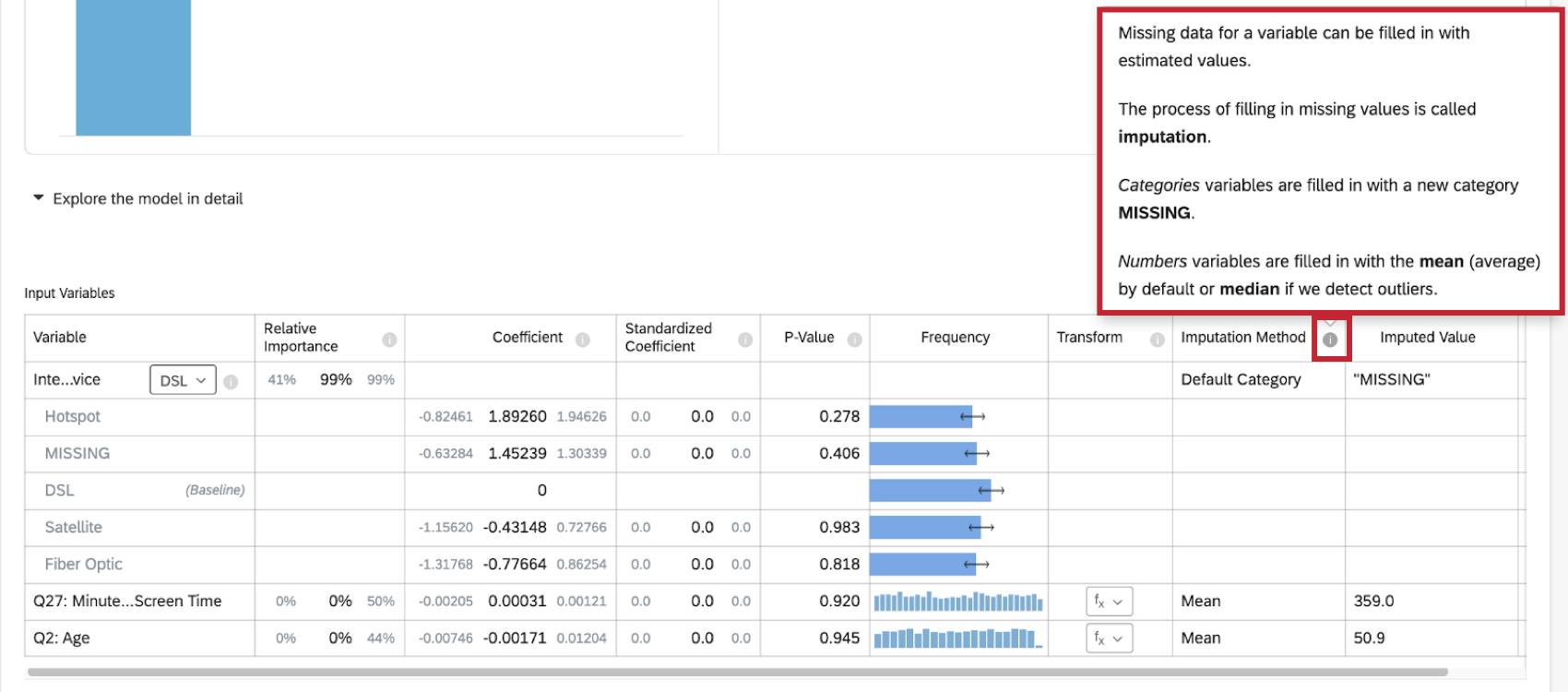
Selezionando Esplora il modello in dettaglio, vengono elencate le variabili di ingresso e di uscita. Le variabili di input vengono fornite con le seguenti informazioni:

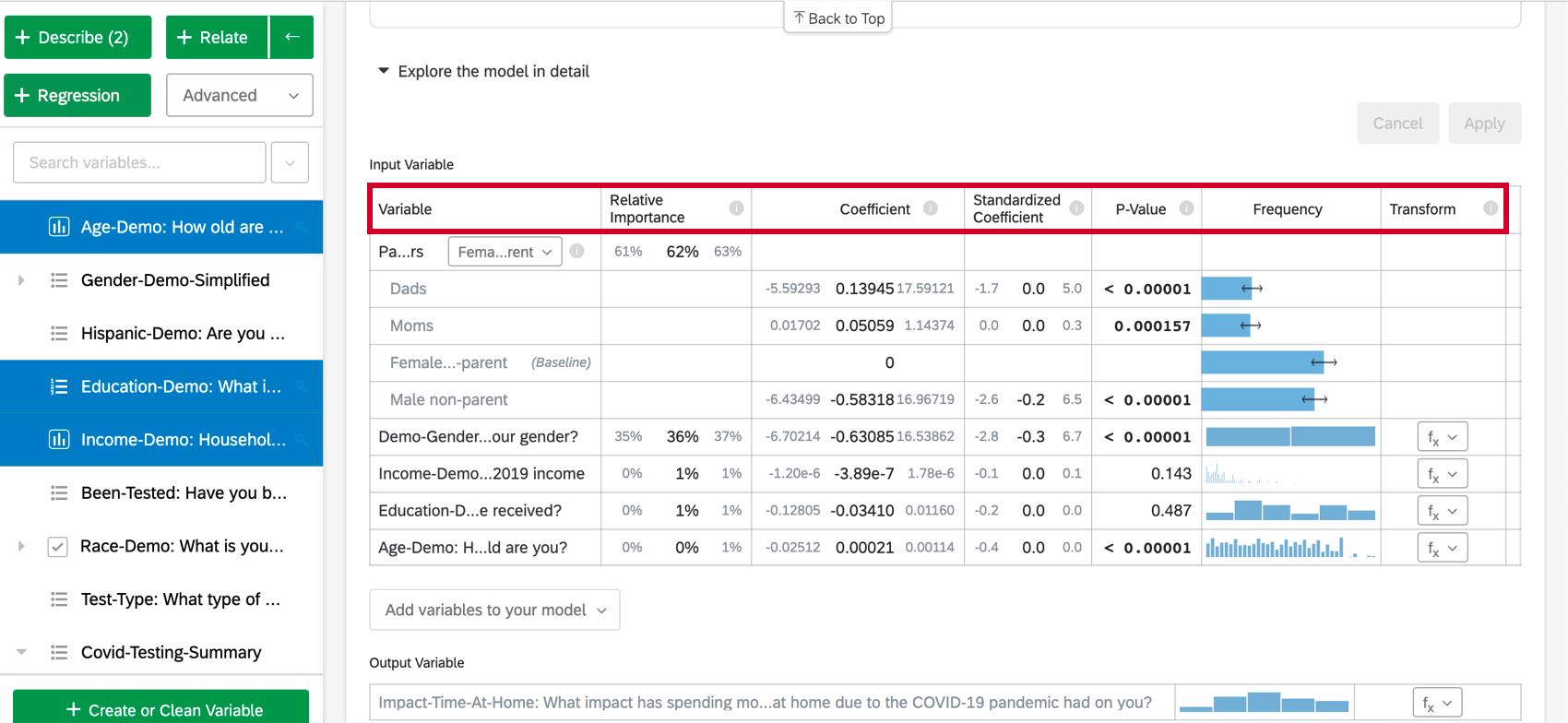
• Importanza relativa: La proporzione del quadrato di r che viene apportata da una singola variabile. L’r-squared è la proporzione della variazione della variabile di risultato che può essere spiegata dalle variabili di input in questo modello. Per maggiori dettagli, vedere Importanza relativa.
• Odds ratio: Rilevante solo per la regressione logistica. L’odds ratio per una data variabile di input indica il fattore di variazione delle probabilità per ogni aumento unitario della variabile esplicativa.
  Esempio: Ad esempio, se l’odds ratio per la soddisfazione del manager è 1,1 e i gruppi della variabile di output sono Soddisfatti e Non soddisfatti, per ogni caso in cui la soddisfazione del manager è superiore di 1, le probabilità della variabile di output di essere soddisfatta sono superiori di 1,1 (10% in più). Se la riga di dati è una categoria, come colore[blu], il coefficiente rappresenta la variazione delle probabilità della variabile di risposta se la variabile RISPOSTE è quella particolare categoria (blu) invece del gruppo “di base” (rosso, verde, ecc.).
• Coefficiente: Ogni aumento di 1 unità di una variabile di input è associato a un aumento del coefficiente della variabile di output. Questi coefficienti sono costruiti sulla base dei risultati dell’analisi dell’importanza relativa e quindi si adattano alla multicollinearità e non corrispondono ai coefficienti che risulterebbero da una regressione standard ai minimi quadrati ordinari.
• Coefficiente standardizzato: Il coefficiente standardizzato è il coefficiente diviso per la varianza della variabile di input. In questo modo ogni variabile viene posta sulla stessa scala, in modo che i loro coefficienti possano essere confrontati più direttamente.
• Valore P: Il valore p è la misura della significatività statistica. Valori più bassi sono associati a minori probabilità che la relazione sia una coincidenza. Per le variabili categoriche, il valore p indica la significatività statistica della differenza tra un gruppo e il gruppo “base” nella variabile.
• Trasformare: Vedere Trasformazione di variabili.

Analisi della regressione OLS

Per la regressione lineare, fare clic su Analizza la diagnostica della regressione OLS e i residui per migliorare il modello sotto la variabile chiave/output per visualizzare i grafici delle previsioni e dei residui. Per ulteriori informazioni, vedere Interpretare i grafici dei residui per migliorare la regressione.

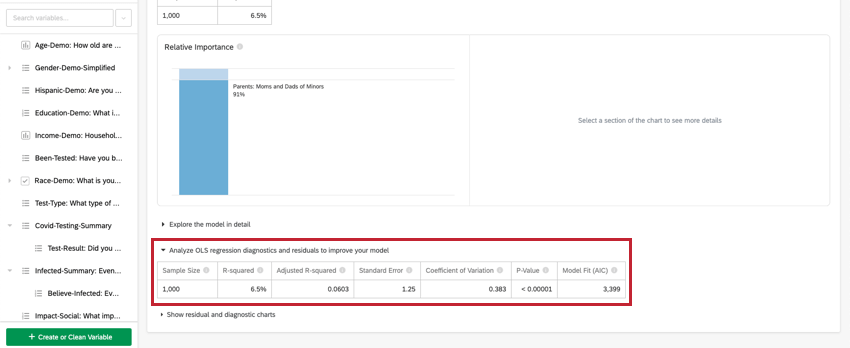
Variabile inclusa

Nell’intestazione superiore della scheda di regressione sono riportate le variabili utilizzate nella regressione.

Fare clic sul nome di una variabile per aprire una nuova finestra in cui è possibile ricodificare o raggruppare i valori. Fare clic sulle frecce per cambiare le variabili di input e di output dell’analisi.

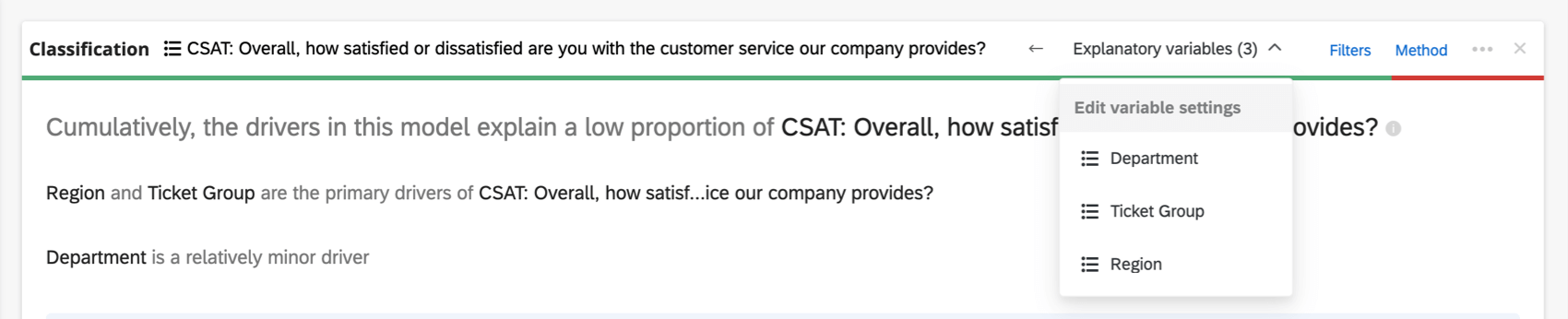
Se le variabili coinvolte sono troppe per essere visualizzate nell’intestazione, sarà disponibile un menu a tendina delle variabili esplicative in cui è possibile scegliere tra le variabili che si desidera ricodificare.

Aggiunta e rimozione di variabili

Una volta creata una scheda di regressione, è possibile aggiungere altre variabili all’analisi seguendo i passaggi seguenti:

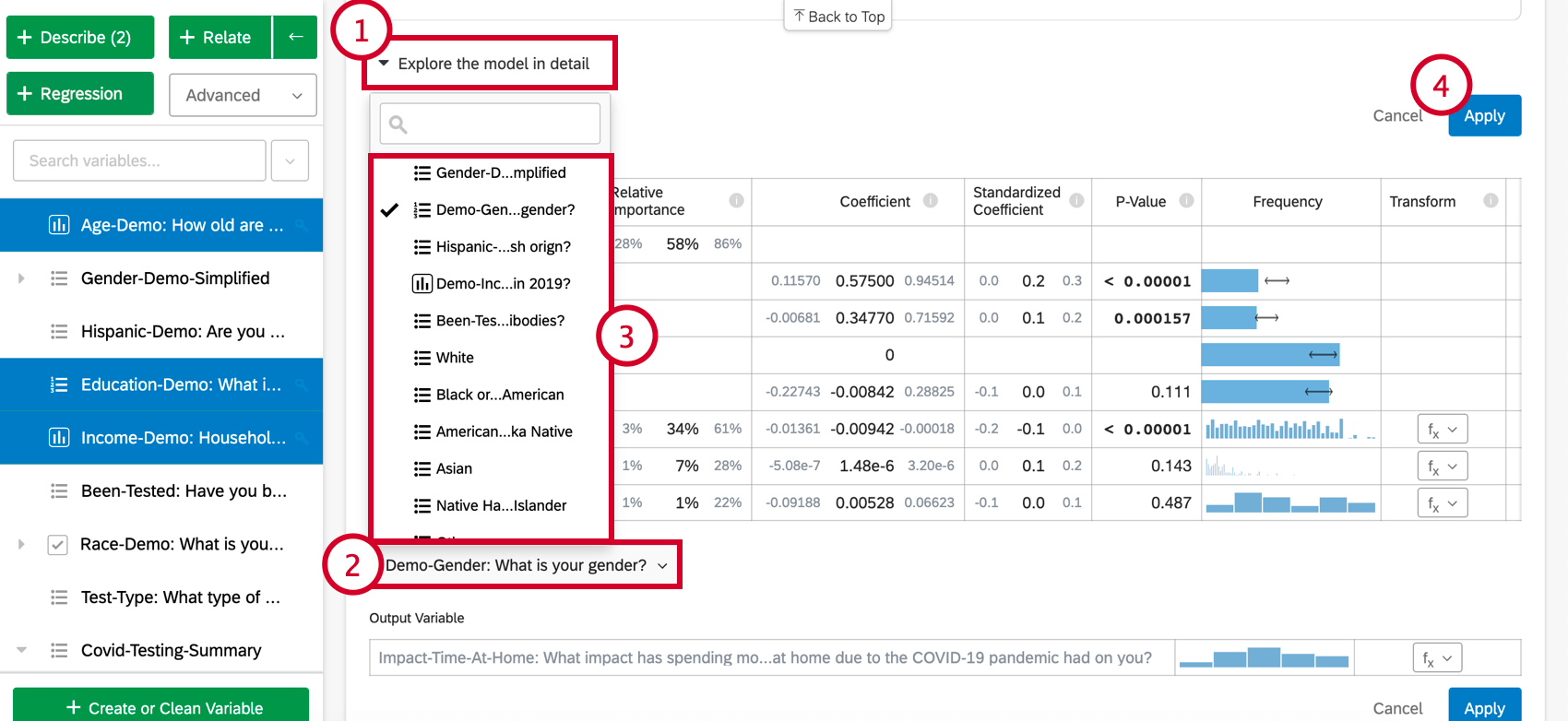
1. Fare clic su Esplora il modello in dettaglio.
2. Selezionare Aggiungi variabili al modello nella parte inferiore della scheda. Verrà visualizzata una lista di variabili che non sono ancora state utilizzate per la regressione.
3. Scegliere una variabile da questa lista.
4. Fare clic su Applica per eseguire nuovamente l’analisi con la nuova variabile inclusa.

Per rimuovere una variabile dalla regressione, passare il mouse sulla variabile desiderata e fare clic sulla X blu all’estrema destra della tabella. Dopo aver scelto le variabili da aggiungere o rimuovere, assicurarsi di selezionare “Applica” per eseguire il nuovo modello.

Imputazione delle variabili

La regressione prenderà in considerazione solo le righe in cui tutte le variabili di input hanno dei dati. Tuttavia, nella raccolta dei dati del sondaggio spesso mancano dei dati, il che può influire negativamente sull’analisi di regressione e sul modello. Se si includono nella regressione solo le righe che non hanno dati mancanti, i risultati dell’analisi possono essere falsati perché il campione non è rappresentativo dell’intero set di dati.

Con l’imputazione, Stats iq inserisce automaticamente i dati mancanti con valori stimati. Quando i dati mancanti vengono completati, è possibile includere una quantità maggiore di dati originali nell’analisi di regressione, ottenendo un modello di regressione con meno distorsioni e in grado di spiegare meglio la variazione della variabile di risultato desiderata.

L’imputazione è automatica, quindi quando si esegue un’analisi di regressione su un set di dati con valori mancanti, il set di dati viene imputato prima di eseguire qualsiasi calcolo.

Fare clic qui per visualizzare un esempio di set di dati prima e dopo l’imputazione delle variabili.

Prima dell’imputazione:
per questa regressione, “Uso dei dati” è la variabile di esito e “Età”, “Servizio Internet” e “Minuti di schermo” sono le variabili di input.

ID riga	Utilizzo dei dati	Età	Servizio Internet	Tempo di schermo (Timing)
1	75	39	Satellite	503
2	19	41	Fibra ottica	52
3	87			434
4	54	23	Satellite
5	14			101
6	75		Satellite
7	81	57	DSL	329

Attenzione: Se si esegue una regressione senza inserire i valori mancanti, saranno incluse solo le righe 1, 2 e 7.

Dopo l’imputazione:

ID riga	Utilizzo dei dati	Età	Servizio Internet	Tempo di schermo (Timing)
1	75	39	Satellite	503
2	19	41	Fibra ottica	52
3	87	50.9	MANCANTE	434
4	54	23	Satellite	359.0
5	14	50.9	MANCANTE	101
6	75	50.9	Satellite	359.0
7	81	57	DSL	329

Consiglio Q: “Servizio Internet” è una variabile categorica, non numerica, quindi il valore mancante viene inserito come “MISSING”.

Metodi di imputazione

Attualmente Stats iQ utilizza i seguenti metodi di imputazione:

• Categoria predefinita: Stats iq creerà un nuovo valore di categoria “MISSING” per inserire i dati mancanti. Questo metodo viene utilizzato per le variabili categoriche.
• Media: Se Stats iQ non rileva alcun outlier nella distribuzione della variabile numerica, i dati mancanti per la variabile vengono completati con il valore medio. Questo metodo viene utilizzato per le variabili numeriche.
• Mediana: Se Stats iQ rileva degli outlier nella distribuzione della variabile numerica, i dati mancanti per la variabile vengono riempiti con il valore mediano. Questo metodo viene utilizzato per le variabili numeriche.

Indicatori di imputazione

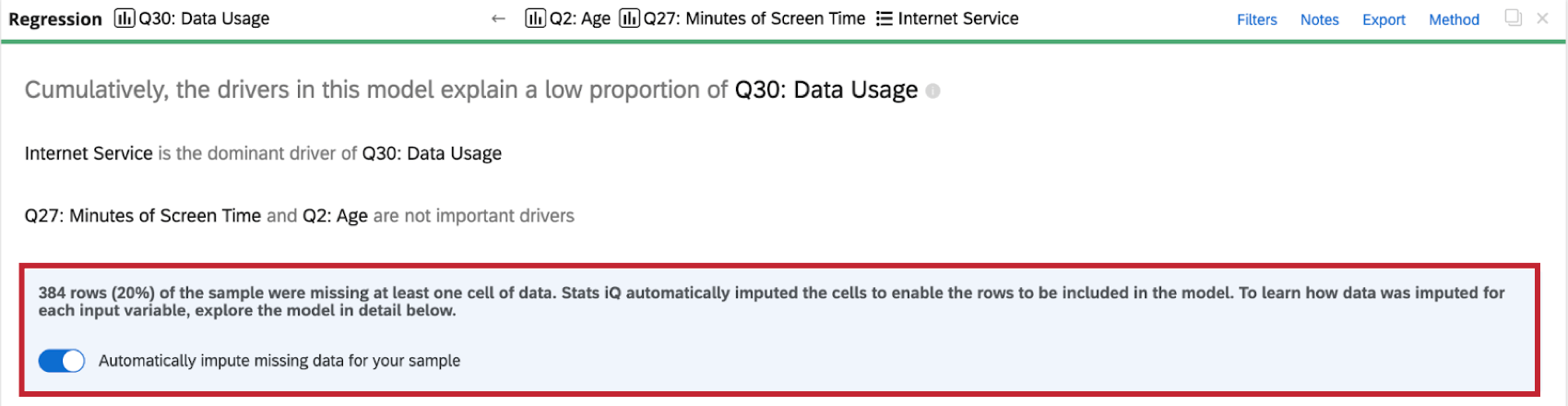
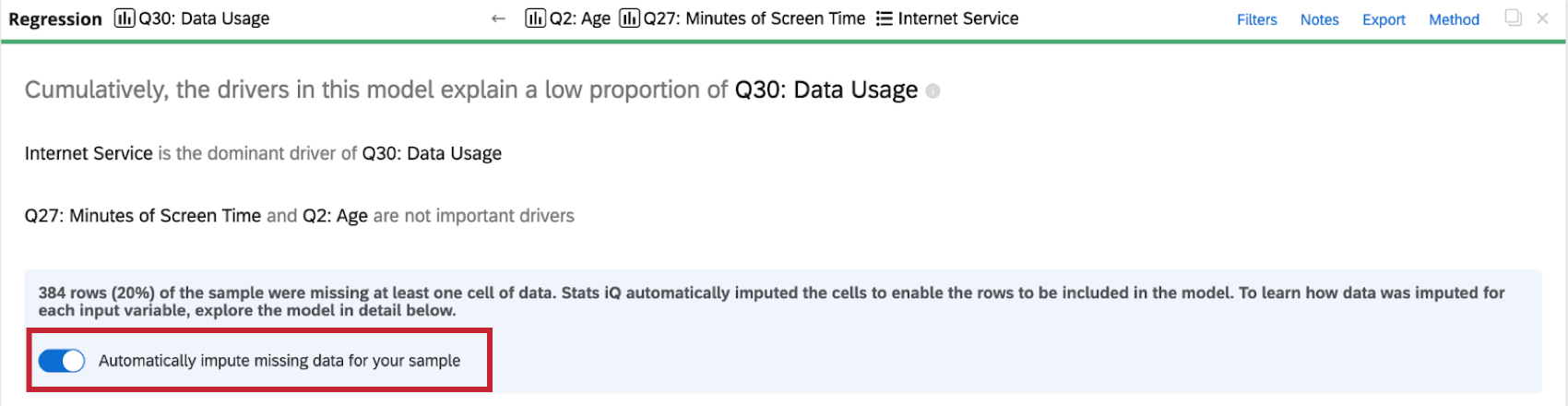
Quando si esegue un’analisi di regressione sul set di dati, si vedrà un indicatore di imputazione nella parte superiore della scheda di regressione.

Ulteriori informazioni sull’imputazione sono disponibili facendo clic sul simbolo di informazione ( i ) avanti a Metodo di imputazione.

Disabilitazione dell’imputazione

Stats iQ applica automaticamente l’imputazione a tutte le schede di regressione. Per disattivare l’imputazione automatica, fare clic su Imputa automaticamente i dati mancanti per il campione nella parte superiore della scheda di regressione.

Avvertenze sull’imputazione

• Se vengono imputati troppi dati, il modello di regressione diventa distorto e inaffidabile. Quando è stato compilato più del 50% del set di dati, Stats iQ avvisa di non trarre conclusioni dai risultati della regressione.
  
• Quando vengono rilevati valori anomali in una qualsiasi delle variabili numeriche di input, Stats iQ imputa le variabili utilizzando il valore mediano anziché la media. In questo caso, Stats iQ vi avvertirà quando esplorerete il modello in dettaglio.
  

Trasformazione delle variabili

Quando si esegue un’analisi di regressione in Stats iQ, si può scoprire che è necessario migliorare il modello. Il modo più comune per migliorare un modello è quello di trasformare una o più variabili, di solito utilizzando un “log” o un’altra trasformazione funzionale.

Trasformare una variabile cambia la forma della sua distribuzione. In generale, i modelli di regressione funzionano meglio con distribuzioni più simmetriche e a campana. Provare diversi tipi di trasformazioni fino a trovarne una che dia questo tipo di distribuzione.

Per trasformare una variabile:

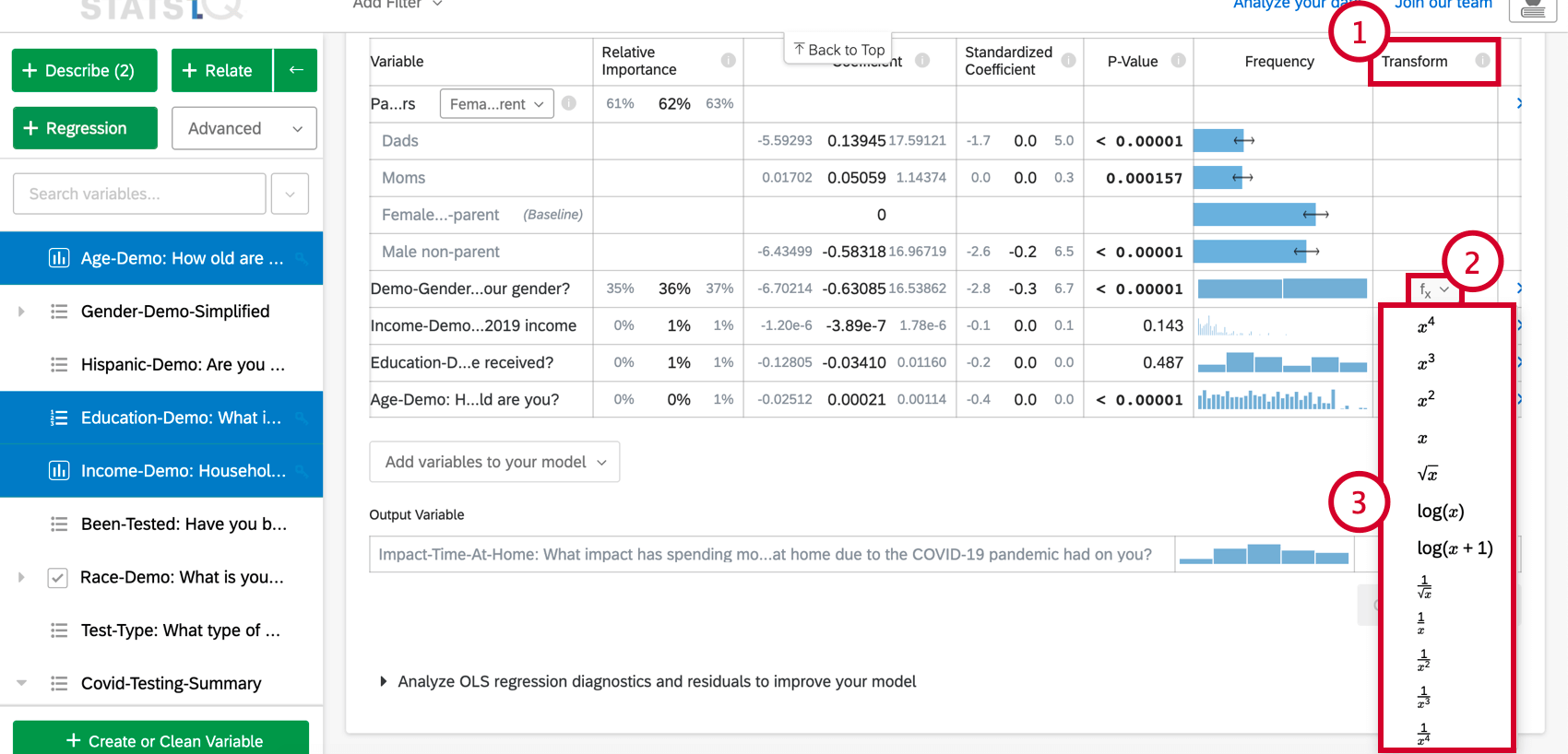
1. Nell’opzione Esplora il modello in dettaglio, scorrere fino alla colonna Trasformazione .
2. Fare clic sul pulsante della funzione(f(x)) per la variabile che si desidera trasformare.
3. Dalla lista, scegliere la funzione che si desidera applicare e Stats iQ ricalcolerà la scheda utilizzando la nuova variabile trasformata.

In Stats iQ sono disponibili le seguenti trasformazioni:

La trasformazione di gran lunga più comune è log(x). Trasforma una distribuzione “di potenza” (come le dimensioni della popolazione di una città), con molti valori più piccoli e un piccolo numero di valori più grandi, in una “distribuzione normale” a forma di campana (come l’altezza), in cui la maggior parte dei valori si raggruppa verso il centro.

Utilizzare log(x+1) se la variabile da trasformare ha alcuni valori pari a zero, poiché log(x) non può essere calcolato quando x è zero.

Per maggiori dettagli su quando trasformare le variabili, vedere Interpretare i grafici dei residui per migliorare la regressione lineare

Altre tecniche di regressione lineare disponibili in Stats iQ

L’importanza relativa combinata con i minimi quadrati ordinari è l’output predefinito per una regressione lineare. Tuttavia, sono disponibili altre opzioni.

Per accedere alla stima M, ai minimi quadrati ordinari e alla regressione di Ridge, fare clic sull’ingranaggio delle impostazioni nell’angolo superiore destro della scheda di regressione. Facendo clic sul nome della tecnica di regressione in Metodi di regressione è possibile modificare la tecnica di regressione utilizzata per la scheda di regressione. Questo può essere fatto solo per la regressione lineare.

• Stima M: Progettata per gestire meglio gli outlier nella variabile di output rispetto ai minimi quadrati ordinari (OLS).
• I minimi quadrati ordinari: I minimi quadrati ordinari (OLS) sono la tecnica di regressione classica. È sensibile agli outlier e ad altre violazioni dei suoi presupposti, pertanto consigliamo metodi più robusti come la stima M. Poiché l’OLS è utilizzato nell’output predefinito dell’importanza relativa, si dovrebbe selezionare questa opzione solo se si è interessati alle funzioni che non sono ancora state adattate nell’output dell’importanza relativa: la previsione degli esiti e l’aggiunta di termini di interazione.
• Regressione di cresta: La regressione Ridge è una tecnica simile alla regressione OLS standard, ma con un parametro di regolazione alfa. Questo parametro alfa aiuta a gestire l’alta varianza e i dati che soffrono di multicollinearità. Se opportunamente regolata, la regressione ridge produce generalmente previsioni migliori rispetto alla OLS, grazie a un migliore compromesso tra bias e varianza. In Stats iQ è possibile scegliere il parametro alfa quando si utilizza la regressione ridge.

Una volta selezionata la stima M, i minimi quadrati ordinari o la regressione di Ridge, sarà possibile vedere il risultato. Il risultato apparirà sotto la sezione Metodi di regressione.

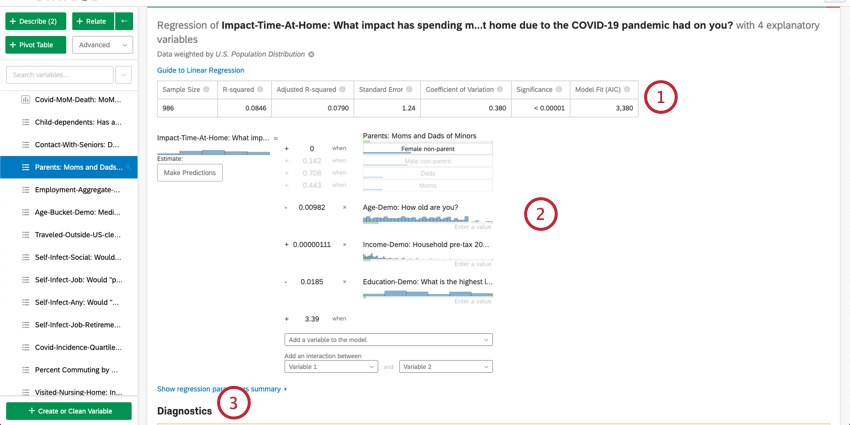
1. Riepilogo numerico: nella parte superiore della scheda è presente un riepilogo dell’analisi di regressione. Questo include la dimensione del campione, i casi mancanti, il metodo, il valore R-quadrato, l’errore standard, il coefficiente di variazione e l’adattamento del modello.
2. Dettagli sul coefficiente: I risultati principali della regressione, l’equazione matematica, si trovano sotto il riepilogo. La variabile di uscita/chiave si trova a sinistra dell’equazione. Le variabili di ingresso si trovano sul lato destro. Se si passa il mouse su una variabile, viene visualizzato un tooltip che spiega in termini chiari come quella variabile contribuisce alla variabile di output. Qui è possibile inserire i valori nell’equazione matematica per stimare i valori della variabile di output. Per ulteriori informazioni, consultare la sezione seguente sulla stima dei valori delle variabili di output.
3. Diagnostica e residui: Stats iQ fornisce una diagnostica che aiuta a valutare l’accuratezza e la validità del modello. Per saperne di più, vedere Interpretare i grafici dei residui per migliorare la regressione lineare o La matrice di confusione e il compromesso precisione-ricordo nella regressione logistica.

Stima dei valori delle variabili di output

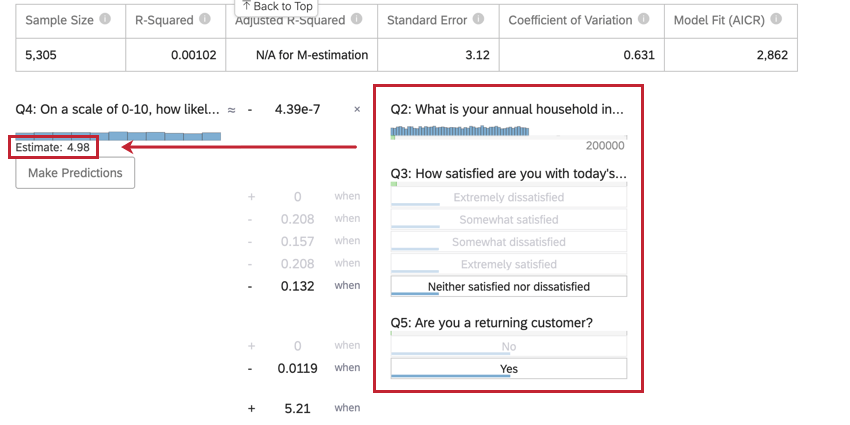
Una volta eseguita una regressione, è possibile utilizzare l’equazione matematica nella sezione Dettagli del coefficiente per stimare i valori delle variabili di output in base ai valori di input selezionati. Sul lato destro dell’equazione, si vedranno le variabili di input. È possibile impostare i valori per ciascuna variabile di input. A sinistra dell’equazione si trova la variabile di uscita. Dopo aver inserito i valori delle variabili di input, l’equazione calcolerà una stima per la variabile di output basata sul modello di regressione.

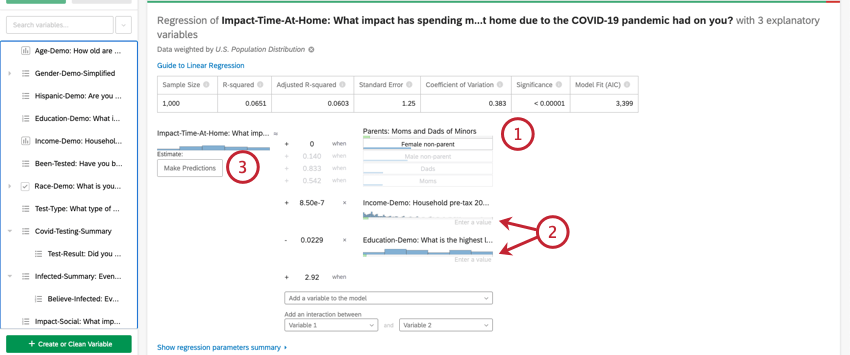
1. Questa variabile di input è una variabile di tipo categoria. Per inserire un valore per le variabili di categoria, fare clic sul valore desiderato dalla lista delle opzioni.
2. Queste variabili di ingresso sono di tipo numerico. Per inserire un valore per le variabili numeriche, fare clic su Inserisci un valore e digitare un numero.
3. Questa variabile è la variabile di uscita dell’equazione di regressione. Dopo aver selezionato i valori per le variabili di ingresso, apparirà un valore stimato per la variabile di uscita, avanti alla dicitura Stima.

Esempio: Nell’esempio seguente, stiamo cercando di prevedere l’NPS dei clienti in base ad alcune variabili di input. Dopo aver selezionato i valori per le variabili di input, possiamo vedere un punteggio NPS stimato di 4,98.

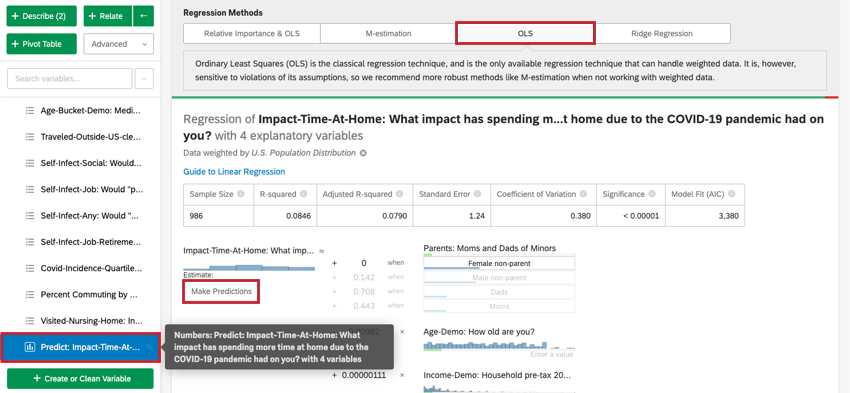
Previsione dei risultati

Di solito, si utilizza l’analisi di regressione in Stats iQ per comprendere la relazione tra le variabili di input e le variabili di output. Tuttavia, una volta creato un modello di regressione, è possibile utilizzarlo anche per prevedere il valore di uscita per le righe di dati in cui sono presenti i valori degli input.

Termini di interazione e altri problemi avanzati

Aggiunta di termini di interazione

Quando si cerca di migliorare il modello di regressione, è possibile aggiungere termini di interazione alle variabili di input esistenti. Si aggiunge un termine di interazione se si sospetta che il valore di una delle variabili di input modifichi l’influenza di una diversa variabile di input sulla variabile di output.

Ad esempio, forse per le persone con bambini presenti durante un soggiorno in hotel, i più giovani sono più soddisfatti dei più anziani, ma per le persone senza bambini presenti, i più giovani sono meno soddisfatti. Ciò significa che c’è un’interazione tra “Bambini presenti” ed “Età”

Selezionando due variabili alla voce Aggiungi un’interazione tra, in fondo alla lista delle variabili di input della scheda, si aggiungerà un termine di interazione alla regressione. Questa funzionalità è disponibile solo in Ordinary Least Squares, M-Estimation e Ridge Regression.

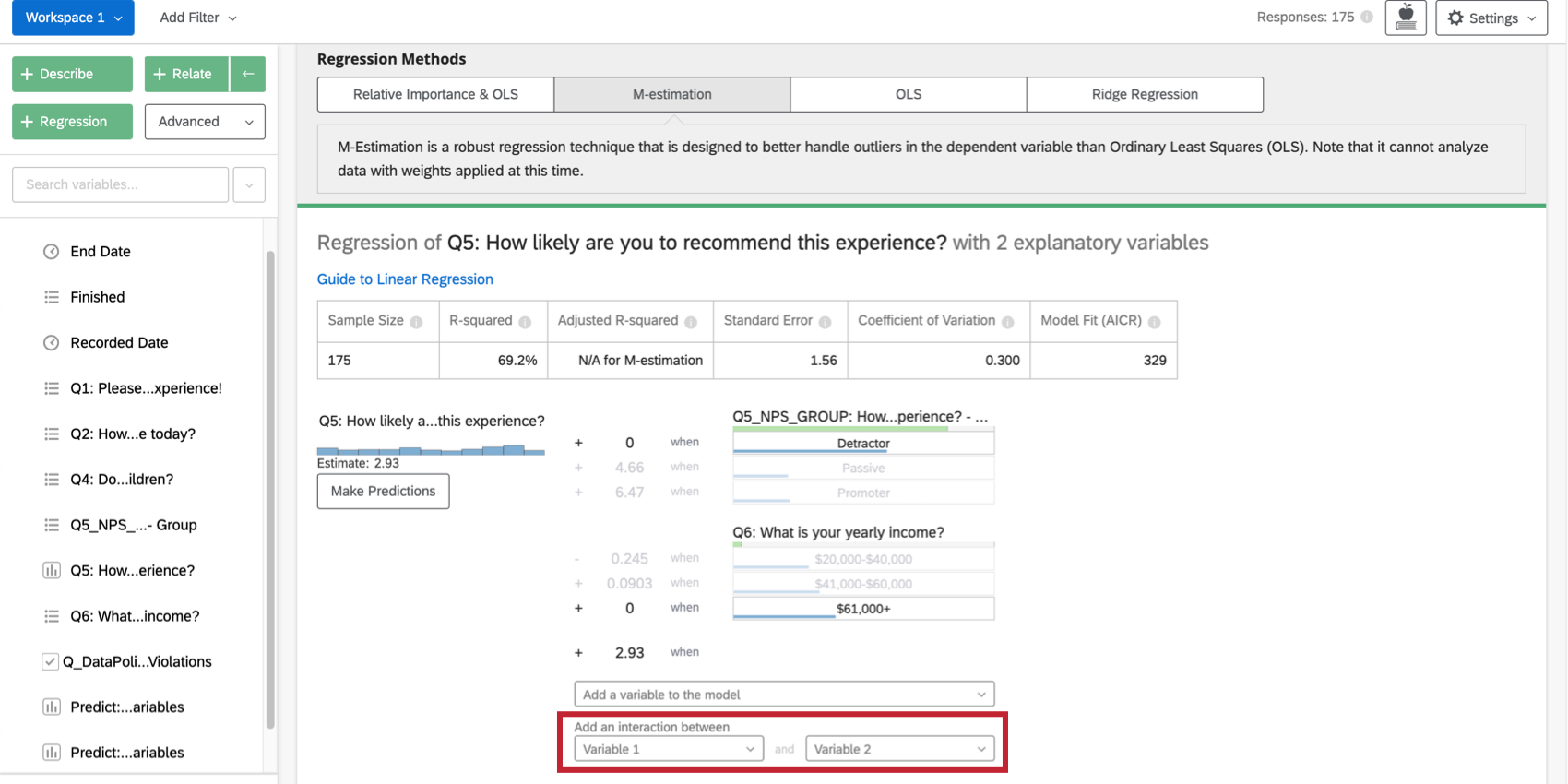
È possibile ottenere lo stesso effetto per le variabili categoriali in un’analisi di importanza relativa creando una nuova variabile che combini le due. Ad esempio, si può combinare la variabile Colore (con i gruppi rosso e verde ) con Dimensione (con i gruppi grande e piccolo ) per ottenere una variabile chiamata DimensioneColore (con i gruppi GrandeRosso, GrandeVerde, PiccoloRosso e PiccoloVerde).

Multicollinearità

La multicollinearità si verifica in un contesto di regressione quando due o più variabili di input sono altamente correlate tra loro.

Quando due variabili sono altamente correlate, la matematica della regressione generalmente attribuisce il massimo valore possibile a una variabile e non all’altra. Ciò si manifesta con un coefficiente maggiore per quella variabile. Ma se il modello viene modificato anche di poco (aggiungendo un filtro, ad esempio), la variabile in cui è stata inserita la maggior parte del valore può cambiare. Ciò significa che anche una piccola modifica può avere un effetto drastico sul modello di regressione.

L’analisi dell’importanza relativa gestisce questo problema in modo da non doversene preoccupare. Se si preferisce utilizzare uno degli altri metodi e il modello presenta questo problema, la presenza di multicollinearità (misurata dal “Fattore di inflazione della varianza”) farà scattare un avviso e suggerirà di rimuovere una variabile o di combinare le variabili facendo la media, ad esempio.

Messaggi di avviso

Stats iQ vi avvisa quando ci sono potenziali problemi con i risultati della regressione. Queste situazioni includono le seguenti:

• Le variabili di input nella regressione non sono statisticamente significative.
• La trasformazione ha rimosso i dati dalla regressione.
• Due o più variabili sono altamente correlate tra loro e rendono i risultati instabili, ovvero la multicollinearità.
• I residui hanno un andamento che suggerisce che il modello potrebbe essere migliorato.
• Una variabile con un solo valore è stata rimossa automaticamente.
• La dimensione del campione è troppo bassa rispetto al numero di variabili di input della regressione.
• È stata aggiunta una variabile di categoria con un numero eccessivo di opzioni di risposta.

FAQ