Analisi corrispondenza (BX)

Informazioni sull’analisi della corrispondenza

L’analisi della corrispondenza rivela le relazioni relative tra e all’interno di due gruppi di variabili, in base ai dati forniti in una tabella di contingenza. Per la percezione del brand, questi due gruppi sono:

1. Brand
2. Attributi che si applicano a questi marchi

Ad esempio, si supponga che un’azienda intenda apprendere quali attributi i consumatori associano a diversi marchi di prodotti per bevande. L’analisi della corrispondenza aiuta a misurare le somiglianze tra i marchi e la forza dei marchi in termini di relazioni con attributi diversi. Comprendere le relazioni relative consente ai titolari del marchio di individuare gli effetti delle azioni precedenti sui diversi attributi correlati al marchio e di decidere le fasi successive da intraprendere.

L’analisi della corrispondenza è preziosa nelle percezioni del brand per un paio di motivi. Quando si tenta di esaminare le relazioni relative tra marchi e attributi, le dimensioni del marchio possono avere un effetto fuorviante; l’analisi della corrispondenza rimuove questo effetto. L’analisi della corrispondenza offre inoltre una visione rapida intuitiva delle relazioni tra attributi del marchio (basata sulla prossimità e la distanza dall’origine) che non viene fornita da molti altri grafici.

In questa pagina ripercorreremo un esempio di come applicare l’analisi della corrispondenza a un caso di utilizzo per diversi (fittizi) marchi di prodotti soda.

Iniziamo con il formato dei dati di input, una tabella di contingenza.

Tabelle situazione eccezionale

Una tabella di contingenza è una tabella bidimensionale con gruppi di variabili nelle righe e nelle colonne. Se i nostri gruppi, come descritto sopra, fossero marchi e attributi associati, eseguiremmo i questionari e riprenderemmo conteggi di risposte diversi associando diversi brand agli attributi indicati. Ogni cella della tabella rappresenta il numero di risposte o conteggi che associano quell’attributo a quel brand. Questa “associazione” viene visualizzata tramite una domanda del sondaggio come “Scegli i brand da un elenco sotto il quale credi di mostrare ___ attributo”.

Qui i due gruppi sono “marche” (righe) e “attributi” (colonne). La cella nell’angolo in basso a destra rappresenta il conteggio delle risposte per il marchio “Brawndo” e l’attributo “Economico”.

Residui (R)

Nell’analisi della corrispondenza, si desidera osservare i residui di ogni cella. Un residuo quantifica la differenza tra i dati osservati e i dati che ci aspetteremmo, supponendo che non vi sia alcuna relazione tra le categorie di riga e di colonna (in questo caso si tratterebbe di marchi e attributi). Un residuo positivo ci mostra che il conteggio per quella coppia di attributi del marchio è molto più alto del previsto, suggerendo una relazione forte; di conseguenza, un residuo negativo mostra un valore inferiore al previsto, suggerendo una relazione più debole. Esaminiamo il calcolo di questi residui.

Un residuo (R) è uguale a: R = P – E, dove P sono le proporzioni osservate ed E sono le proporzioni attese per ogni cellula.  Ripartiamo queste proporzioni osservate e attese!

Proporzioni osservate (P)

Una proporzione osservata (P) è uguale al valore in una cella diviso per la somma totale di tutti i valori della tabella. Quindi per la nostra tabella delle contingenze di cui sopra, la somma totale sarebbe: 5 + 7 + 2 + 18 … + 16 = 312. Divisione di ogni valore cella per il totale dei risultati nella tabella sottostante per le proporzioni osservate (P).

Ad esempio, nella cella in basso a destra, abbiamo preso il valore cella iniziale di 16/312 = 0,051. Questo ci dice la proporzione del nostro intero grafico che l’abbinamento di Brawndo e Economic rappresenta sulla base dei nostri dati raccolti.

Masse di righe e colonne

Qualcosa che possiamo calcolare facilmente dalle nostre proporzioni osservate, e che verrà usato molto più tardi, sono le somme delle righe e delle colonne della nostra tabella di proporzioni, note come masse di righe e colonne. La massa di una riga o di una colonna è la proporzione di valori per quella riga/colonna. La massa di fila per “Butterbeer,” guardando il nostro grafico sopra, sarebbe 0,016 + 0,022 + 0,006, dandoci 0,044.

Facendo calcoli simili, alla fine:

Proporzioni previste (E)

Le proporzioni previste (E) sarebbero quelle che ci aspettiamo di vedere nella proporzione di ogni cella, presupponendo che non vi sia alcuna relazione tra righe e colonne. Il valore previsto per una cella sarebbe la massa della riga della cella moltiplicata per la massa della colonna di tale cella.

Si veda nella cella in alto a sinistra, la massa della riga per Butterbeer moltiplicata per la massa della colonna per Tasty, 0,044 * 0,182 = 0,008.

Ora possiamo calcolare la nostra tabella dei residui (R), dove R = P – E. I residui quantificano la differenza tra le proporzioni dei dati osservate e le proporzioni di dati previste, se presupponiamo che non vi sia alcuna relazione tra le righe e le colonne.

Prendendo il nostro valore più negativo di -0,045 per Squishee ed Economico, quello che interpreteremmo qui è che c’è un’associazione negativa tra Squishee ed Economico; Squishee ha molta meno probabilità di essere vista come “Economica” rispetto alle nostre altre marche di bevande.

Residui indicizzati (I)

Tuttavia, vi sono alcuni problemi con la sola lettura dei residui.

Osservando la prima riga della tabella di calcolo dei residui di cui sopra, vediamo che tutti questi numeri sono molto vicini allo zero. Non dovremmo trarre l’ovvia conclusione che Butterbeer non è legata ai nostri attributi, poiché questa supposizione non è corretta. La spiegazione vera e propria sarebbe che le proporzioni osservate (P) e quelle attese (E) sono piccole perché, come ci dice la nostra massa di fila, solo il 4,4% del campione è Butterbeer.

Questo solleva un grosso problema nell’analisi dei residui, poiché ignorando il numero effettivo di record nelle righe e nelle colonne, i risultati sono distorti verso le righe/colonne con masse maggiori. Possiamo risolvere questo problema dividendo i residui per le proporzioni previste (E), fornendo una tabella dei residui indicizzati (I, I = R / E):

I residui indicizzati sono facili da interpretare: maggiore è il valore della tabella, maggiore è la proporzione osservata rispetto alla proporzione prevista.

Ad esempio, prendendo il valore in alto a sinistra, Butterbeer ha il 95% di probabilità in più di essere vista come “Tasty” di quanto ci aspetteremmo se non ci fosse relazione tra questi marchi e attributi. Mentre al valore in alto a destra, Butterbeer ha il 65% di probabilità in meno di essere vista come “Economica” di quanto ci aspetteremmo – dato che non c’è alcuna relazione tra i nostri marchi e gli attributi.

Considerati i residui indicizzati (I), le proporzioni previste (E), le proporzioni osservate (P) e le masse di righe e colonne, riusciamo a calcolare i valori dell’analisi della corrispondenza per il grafico!

Calcolo delle coordinate per l’analisi della corrispondenza

Scomposizione valore singolare (SVD)

Il nostro primo passo è calcolare la scomposizione Singular Value, o SVD. Il SVD ci fornisce valori per calcolare la varianza e tracciare le nostre righe e colonne (marchi e attributi).

Calcoliamo la SVD sul residuo standardizzato (Z), dove Z = I * sqrt(E), dove I è il nostro residuo indicizzato, ed E è le nostre proporzioni attese. La moltiplicazione per E fa sì che il nostro SVD sia ponderato, in modo tale che le celle con un valore atteso più elevato ricevano un peso maggiore e viceversa, il che significa che poiché i valori attesi sono spesso correlati alla dimensione del campione, le celle “più piccole” della tabella, in cui l’errore di campionamento sarebbe stato maggiore, sono depesate. Pertanto, l’analisi della corrispondenza utilizzando una tabella delle contingenze è relativamente robusta per i valori fuori norma causati dall’errore di campionamento.

Tornando al nostro SVD, abbiamo: SVD = svd(Z). Una decomposizione di valore singolare genera 3 uscite:

Un vettore, d, contenente i valori singolari.

Una matrice, u, contenente i vettori singolari di sinistra (marche).

Una matrice, v, contenente i vettori singolari di destra (attributi).

I vettori singolari di sinistra corrispondono alle categorie nelle righe della tabella, mentre i vettori singolari di destra corrispondono alle colonne. Ciascuno dei valori singolari, per il calcolo della varianza, e i vettori corrispondenti (cioè colonne di u e v), per tracciare le posizioni, corrispondono a una dimensione. Le coordinate utilizzate per tracciare le categorie di righe e colonne per il grafico di analisi della corrispondenza vengono derivate dalle prime due dimensioni.

Scostamento espresso dalle nostre dimensioni

I valori singolari quadrati sono noti come autovalori (d^2). Gli autovalori nel nostro esempio sono 0.0704, 0.0129 e 0.0000. L’espressione di ogni autovalore come proporzione della somma totale ci indica la quantità di varianza acquisita in ogni dimensione della nostra analisi della corrispondenza, in base al valore singolare di ogni dimensione; otteniamo l’84,5% della varianza espressa dalla prima dimensione e il 15,5% nella seconda dimensione (la terza dimensione spiega lo 0% della varianza).

Analisi della corrispondenza standard

Ora siamo dotati delle risorse per calcolare la forma di base dell’analisi della corrispondenza, utilizzando quelle che sono note come coordinate standard, calcolate dai nostri vettori singolari di sinistra e destra. In precedenza, ponderavamo i residui indicizzati prima di eseguire il SVD. Per ottenere coordinate che rappresentano i residui indicizzati, ora dobbiamo sbilanciare gli output del SVD, dividendo ogni riga dei vettori singolari di sinistra per la radice quadrata delle masse delle righe e dividendo ogni colonna dei vettori singolari di destra per la radice quadrata delle masse delle colonne, ottenendo le coordinate standard delle righe e delle colonne per la plotting.

Coordinate standard del marchio:

Coordinate standard attributo:

Utilizziamo le due dimensioni con la varianza più elevata acquisite per la tracciatura, la prima dimensione sull’asse X e la seconda sull’asse Y, generando il grafico di analisi della corrispondenza standard.

Abbiamo gettato le basi dei calcoli di cui abbiamo bisogno per l’analisi della corrispondenza standard, Nella sezione successiva esploreremo i pro e i contro dei diversi stili di analisi della corrispondenza e che meglio si adatta ai nostri scopi di aiuto nell’analisi delle percezioni del brand.

Tipi di analisi della corrispondenza

Analisi corrispondenza principale riga/colonna

L’analisi della corrispondenza standard è semplice da calcolare e da essa è possibile ricavare risultati solidi. Tuttavia, la corrispondenza standard è una scelta scarsa per le nostre esigenze; le distanze tra le coordinate delle righe e delle colonne sono esagerate, e non c’è un’interpretazione diretta delle relazioni tra le categorie di riga e di colonna. Ciò che vogliamo per interpretare le relazioni tra le coordinate delle righe (del marchio) e per interpretare le relazioni tra le categorie di riga e colonna è la normalizzazione principale di riga (o, se i nostri marchi erano sulle nostre colonne, la normalizzazione principale di colonna).

Per la normalizzazione del principale riga, si desidera utilizzare le coordinate standard calcolate sopra per i valori (attributo) della colonna, ma si desidera calcolare le coordinate principali per i valori della riga (marchio). Calcolare le coordinate principali è semplice come prendere le coordinate standard, e moltiplicarle per i corrispondenti valori singolari (d). Quindi, per le nostre righe, vogliamo semplicemente moltiplicare le coordinate delle righe standard per i valori singolari (d), mostrati nella tabella sottostante. Per la normalizzazione del principale colonna moltiplicheremmo semplicemente le colonne anziché le righe per i valori singolari (d).

Sostituendo nelle nostre coordinate principali le nostre righe (marchi), finiamo con:

Poiché abbiamo scalato in base ai nostri valori singolari, le nostre coordinate principali per le nostre righe rappresentano la distanza tra i profili delle righe della nostra tabella originale; si può interpretare le relazioni tra le nostre coordinate di riga nel nostro grafico di analisi della corrispondenza in base alla loro vicinanza l’una all’altra.

La distanza tra le nostre coordinate di colonna, dal momento che si basano su coordinate standard, è ancora esagerata. Inoltre, la nostra scala in base ai nostri valori singolari in una sola delle due categorie (righe/colonne) ci ha dato un modo di interpretare le relazioni tra le categorie di riga e di colonna. Dato un valore di riga e un valore di colonna, ad esempio Butterbeer (riga), e Tasty (colonna), più lunga è la loro distanza dall’origine, più forte è la loro associazione con altri punti sulla mappa. Inoltre, più piccolo è l’angolo tra i due punti (Butterbeer e Tasty), maggiore è la correlazione tra i due.

La distanza dall’origine combinata con l’angolo tra i due punti è l’equivalente di prendere il prodotto del punto; il prodotto del punto tra un valore di riga e di colonna misura l’intensità dell’associazione tra i due. Infatti, quando la prima e la seconda dimensione spiegano tutta la varianza nei dati (somma 100%), il prodotto del punto è direttamente uguale al residuo indicizzato delle due categorie. Qui, il prodotto del punto sarebbe la distanza all’origine dei due punti moltiplicata per il coseno dell’angolo che li separa; .59*2,12*cos(41) = .94. Tenendo conto degli errori di arrotondamento, è lo stesso valore residuo indicizzato di .95. Quindi, angoli più piccoli di 90 gradi rappresentano un residuo indicizzato positivo e quindi un’associazione positiva, e angoli più grandi di 90 gradi rappresentano un’associazione negativa o residua indicizzata.

Analisi della corrispondenza principale riga scalata

Guardando il grafico sopra per la normalizzazione dei principali di riga, abbiamo un’osservazione semplice: i punti delle colonne (tratti) sono molto più sparsi e i punti per le nostre righe (marchi) sono raggruppati intorno all’origine. Questo può rendere l’analisi del grafico per occhio piuttosto difficile e poco intuitiva, e talvolta impossibile leggere le categorie di riga se tutte si sovrappongono. Fortunatamente, esiste un modo semplice per scalare il grafico per portare le colonne, pur mantenendo la capacità di utilizzare il prodotto puntato (distanza dall’origine e angolo tra i punti) per analizzare le relazioni tra i nostri punti riga e colonna, nota come normalizzazione principale di riga scalata.

La normalizzazione principale di riga scalata prende la normalizzazione principale di riga e scala le coordinate della colonna nello stesso modo in cui abbiamo scalato l’asse x delle coordinate delle righe, in altre parole, le nostre coordinate di colonna sono scalate in base al primo valore dei nostri valori singolari (d). I valori di riga sono uguali alla normalizzazione del valore principale della riga, ma ora le coordinate delle colonne vengono ridimensionate di un fattore costante.

Ciò significa per noi che le coordinate delle colonne sono scalate per adattarsi molto meglio alle nostre coordinate di riga, rendendo molto più semplice l’analisi delle tendenze. Poiché abbiamo scalato tutte le coordinate delle colonne con lo stesso fattore costante, abbiamo contratto la dispersione delle nostre coordinate di colonna sulla mappa, ma non abbiamo apportato modifiche alle loro relatività; utilizziamo ancora il prodotto del punto per misurare la forza delle associazioni. L’unica modifica è che quando la prima e la seconda dimensione coprono tutta la varianza nei dati, invece che il residuo indicizzato è uguale al prodotto puntato delle due categorie, è ora uguale al prodotto punto scalato delle due categorie, ovvero il prodotto puntato scalato per un valore costante del nostro primo valore singolare (d). L’interpretazione del grafico rimane invariata rispetto alla normalizzazione del principale riga.

Analisi della corrispondenza principale

Una forma finale di analisi della corrispondenza che menzioneremo è l’analisi della corrispondenza principale, nota anche come mappa simmetrica, scala francese o analisi della corrispondenza canonica. Invece di moltiplicare solo le righe o le colonne standard per i valori singolari (d) come nell’analisi della corrispondenza principale di riga/colonna, moltiplichiamo entrambi i valori per i valori singolari. Pertanto i valori delle colonne standard, moltiplicati per i valori singolari, diventano:

Mettendoli insieme ai nostri valori di riga calcolati nell’analisi principale delle righe, otteniamo:

L’analisi canonica della corrispondenza scala sia le coordinate di riga che di colonna in base ai valori singolari. Ciò significa che possiamo interpretare le nostre relazioni tra le nostre coordinate di riga esattamente come abbiamo fatto nella riga principale analisi della corrispondenza (basata sulla prossimità), E possiamo interpretare le nostre relazioni tra le coordinate delle colonne in modo simile all’analisi della corrispondenza principale delle colonne; possiamo analizzare le relazioni tra i marchi e le relazioni tra gli attributi. Perdiamo anche il clustering di righe/colonne al centro della mappa dall’analisi principale di riga/colonna. Ciò che però perdiamo dall’analisi della corrispondenza canonica, è un modo di interpretare le relazioni tra i nostri brand e gli attributi, qualcosa di molto utile nelle percezioni del brand.

Confronto side-by-side

Analisi corrispondenza standard

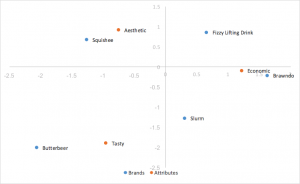
Lo stile più semplice di analisi della corrispondenza da calcolare, utilizzando vettori singolari di destra e sinistra di SVD divisi per le masse di righe e colonne. Le distanze tra le coordinate delle righe e delle colonne sono esagerate e non esiste un’interpretazione diretta delle relazioni tra le categorie di riga e di colonna.

Normalizzazione principale riga – Analisi corrispondenza

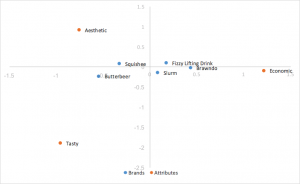
Utilizza coordinate standard dall’alto, ma moltiplica le coordinate delle righe per i valori singolari da normalizzare. Le relazioni tra righe (marchi) si basano sulla distanza l’una dall’altra. Le distanze delle colonne (attributo) sono ancora esagerate. Le relazioni tra righe e colonne possono essere interpretate dal prodotto punto. Le righe (marche) tendono ad essere goffrate al centro.

Analisi corrispondenza normalizzazione principale riga scalata

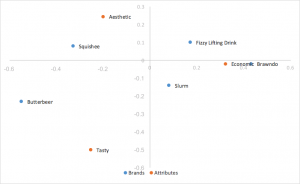
Prende la normalizzazione principale della riga e scala le coordinate delle colonne per una costante del primo valore singolare. Stesse interpretazioni disegnate come normalizzazione dei punti principali delle righe, che sostituiscono il prodotto a punti con quello scalato. Aiuta a rimuovere i grumi delle righe al centro. Questo è lo stile di analisi della corrispondenza che preferiamo.

Analisi corrispondenza normalizzazione principale (simmetrico, mappa francese, canonica)

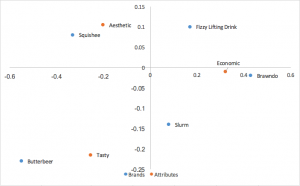
Un’altra forma popolare di analisi della corrispondenza che utilizza le coordinate normalizzate principali sia nelle righe che nelle colonne. Le relazioni tra le righe (marche) possono essere interpretate in base alla distanza l’una dall’altra; lo stesso si può dire per le colonne (attributi). Non è possibile tracciare alcuna interpretazione per le relazioni tra righe e colonne.

Riepilogo in corso

In conclusione, l’analisi della corrispondenza viene utilizzata per analizzare le relazioni relative tra e all’interno di due gruppi; nel nostro caso, questi gruppi sarebbero marchi e attributi.

L’analisi della corrispondenza elimina gli scarti nei risultati di diverse masse tra i gruppi utilizzando residui indicizzati. Per la percezione del brand per l’analisi della corrispondenza, utilizziamo la normalizzazione della riga principale (o della colonna principale se i marchi sono posizionati sulle colonne), in quanto questo ci consente di analizzare le relazioni tra i diversi marchi in base alla loro vicinanza l’uno all’altro, e ci permette anche di analizzare le relazioni tra i marchi e gli attributi in base alla loro distanza dall’origine combinata con l’angolo tra essi e l’origine (il prodotto del punto), al sacrificio di misrappresentazioni della relazione tra gli attributi con gli attributi esagerati (che non ci interessa). Utilizziamo la normalizzazione principale riga/colonna in scala per semplificare l’analisi del grafico a costo zero. Vogliamo ricordare che sommiamo lo scostamento spiegato dalle etichette degli assi X e Y (la prima e la seconda dimensione) per visualizzare lo scostamento totale acquisito nella mappa; più basso è il numero, più lo scostamento inspiegato è presente nei dati e più il grafico risulta fuorviante.

Un’ultima cosa da ricordare è che l’analisi della corrispondenza mostra solo relatività da quando abbiamo eliminato il fattore di massa dei nostri dati; il nostro grafico non ci dirà nulla su quali marchi hanno i punteggi “più alti” negli attributi. Una volta capito come creare e analizzare i grafici, l’analisi della corrispondenza è un potente strumento che ignora gli effetti di dimensionamento del brand per fornire informazioni potenti e facili da interpretare sulle relazioni tra i brand e all’interno di essi e sui loro attributi applicabili.

FAQ