Régression et importance relative
A propos de la régression et de l’importance relative
La régression montre comment plusieurs variables d’entrée influencent ensemble une variable de sortie. Par exemple, si les entrées “Nombre d’années en tant que client” et “Taille de l’entreprise” sont toutes deux en corrélation avec la sortie “Satisfaction” et entre elles, vous pouvez utiliser la régression pour déterminer laquelle des deux entrées est la plus importante pour créer la “Satisfaction”L’
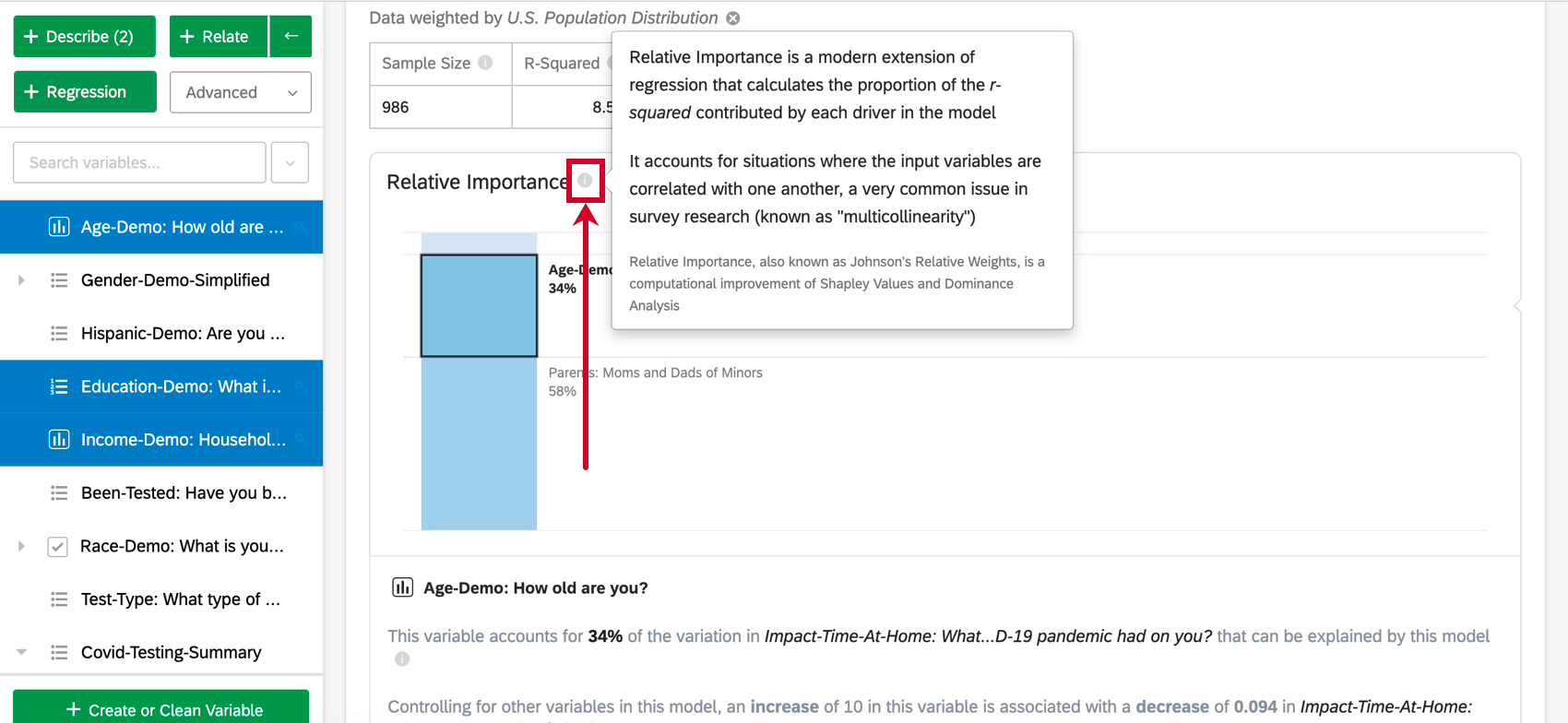
analyse de l’importance relative est la meilleure méthode de régression pour les données d’enquête et le résultat par défaut des régressions effectuées dans Stats iQ. L’importance relative est une extension moderne de la régression qui tient compte des situations où les variables d’entrée sont corrélées entre elles, un problème très courant dans les enquêtes (connu sous le nom de “multicollinéarité”). L’importance relative est également connue sous le nom de pondérations relatives de Johnson, est une variante de l’analyse de Shapley et est étroitement liée à l’analyse de dominance.
Vous trouverez ci-dessous des instructions sur la manière de mettre en place une régression dans Stats iQ. Pour plus d’informations sur les aspects analytiques de l’analyse de régression, veuillez consulter les pages suivantes :
- Guide convivial de la régression linéaire
- Interprétation des diagrammes de résidus pour améliorer votre régression linéaire
- Guide pratique de la régression logistique
- La matrice de confusion et le compromis précision-rappel dans la régression logistique
  ;
Pour la régression linéaire, Relative Importance in Stats iQ suit les techniques décrites dans Lipovetsky, Stan & ; Conklin, Michael. (2001). Analyse de la régression dans l’approche de la théorie des jeux. Modèles stochastiques appliqués aux entreprises et à l’industrie. 17. 319 – 330. 10.1002/asmb.446.
Pour la régression logistique, Relative Importance in Stats iQ suit les techniques décrites dans Tonidandel, Scott & ; LeBreton, James. (2009). Détermination de l’importance relative des prédicteurs dans la régression logistique : Une extension de l’analyse de la pondération relative. Méthodes de recherche en organisation – MÉTHODES DE RECHERCHE EN ORGANISATION. 12. 10.1177/1094428109341993.
Sélection des variables pour les cartes de régression
La création d’une carte de régression vous permettra de comprendre comment la valeur d’une variable de votre ensemble de données est influencée par les valeurs des autres variables.
Lors de la sélection des variables, une variable aura une clé à côté d’elle. Pour la régression, la variable clé sera la variable de sortie. Chaque autre variable sélectionnée après la variable clé sera une variable d’entrée. En d’autres termes, nous essayons d’expliquer comment la valeur de la variable de sortie est déterminée par les variables d’entrée.
Éléments à prendre en compte lors de la sélection des variables pour la régression :
- Vous pouvez modifier la variable clé en cliquant sur l’icône de clé située à côté de n’importe quelle variable dans le volet des variables.
- Si le nombre de variables sélectionnées est supérieur au nombre de réponses dont vous disposez, la régression ne s’effectuera pas.
- Vous pouvez sélectionner jusqu’à 25 variables d’entrée. Cependant, vous devriez essayer de sélectionner de 1 à 10 variables d’entrée, sinon vos résultats pourraient devenir très compliqués.
Si vous souhaitez inclure un grand nombre de variables dans une analyse, envisagez les approches suivantes :
- Effectuez quelques régressions initiales et excluez les variables qui ont très peu d’importance dans le modèle.
- Combiner plusieurs variables, par exemple en calculant une moyenne.
- Si la structure de vos informations le permet, vous pouvez utiliser un processus d’importance relative en deux étapes, comme décrit ici à la page 341.
Exemple : Imaginons que vous disposiez de dix mesures de la satisfaction des employés en matière d ‘autonomie et de dix mesures de la satisfaction des employés en matière de rémunération.
- Faites la moyenne de ces groupes en deux variables de synthèse différentes – une pour l’autonomie et une pour la rémunération.
- Effectuez une analyse de l’importance relative avec la satisfaction globale comme résultat et les deux variables de synthèse comme données d’entrée pour voir quel groupe est le plus important.
- Effectuez ensuite une analyse de l’importance relative avec la satisfaction globale comme résultat et uniquement les dix variables d’autonomie comme données d’entrée afin de déterminer celles qui sont les plus importantes au sein de ce groupe.
- Effectuez une analyse de l’importance relative avec la satisfaction globale comme résultat et uniquement les dix variables de rémunération comme données d’entrée afin de déterminer celles qui sont les plus importantes au sein de ce groupe.
Une fois que vous avez sélectionné vos variables, cliquez sur Régression pour effectuer une régression.
Astuce : en haut de la carte de régression se trouve une ligne verte (et parfois rouge). Si vous cliquez dessus, vous verrez le nombre de réponses marquées comme “incluses” ou “manquantes” pour cette carte spécifique.
- Inclus: Les répondants qui ont répondu à la question pour chaque question ou point de données utilisé dans l’analyse de régression, ou dont les données pour les variables d’entrée manquantes ont été imputées. Ces données seront utilisées dans l’analyse de régression.
- Manquant: Répondants pour lesquels il manque une valeur pour la variable dépendante du résultat. Ces données ne seront pas utilisées dans l’analyse de régression.
Types de régression
Il existe deux types principaux de régression dans Stats iQ. Si la variable de sortie est une variable numérique, Stats iQ effectuera une régression linéaire. Si la variable de sortie est une variable catégorielle, Stats iQ effectuera une régression logistique.
Plus précisément, les types de régression que Stats iQ effectuera sont les suivants :
Régression linéaire
L’importance relative est combinée aux moindres carrés ordinaires (MCO). Le résultat est une combinaison des deux analyses :
- Importance relative: Tout ce qui figure dans cette section provient de l’Importance Relative, à l’exception du r-carré, qui provient de la régression MCO.
- Explorer le modèle en détail: Tout dans cette section provient de l’Importance Relative, sauf les distributions, qui sont tirées des données elles-mêmes.
- Analysez les diagnostics et les résidus de la régression par les MCO afin d’améliorer votre modèle: Tout ce qui est dit dans cette section provient de la régression par les MCO.
Régression logistique
La régression logistique est une méthode de classification binaire utilisée pour comprendre les facteurs d’un résultat binaire (par exemple, oui ou non) en fonction d’un ensemble de variables d’entrée. Si vous effectuez une régression sur une variable de sortie comportant plus de deux groupes, Stats iQ sélectionnera un groupe et regroupera les autres pour en faire une régression binaire (vous pouvez modifier le groupe analysé après l’exécution de la régression).
Importance relative
Les variables d’entrée des données d’enquête sont souvent fortement corrélées entre elles ; il s’agit d’un problème appelé “multicolinéarité” Cela peut conduire à des résultats de régression qui augmentent artificiellement l’importance d’une variable et diminuent l’importance d’une autre variable corrélée. L’importance relative est reconnue comme la meilleure méthode pour en tenir compte.
L’importance relative (en particulier les pondérations relatives de Johnson) ne souffre pas de ce problème et équilibrera de manière adéquate l’importance des variables d’entrée, quel que soit le type de régression utilisé. Elle permet également de calculer la pondération relative (ou l’importance relative) de chaque variable, c’est-à-dire la proportion de la variation explicable de la production qui est due à cette variable. Il s’agit d’une série de pourcentages dont la somme est égale à 100 %.
La technologie de l’information donne des résultats similaires à ceux d’une série de régressions, une pour chaque variation des variables d’entrée. Par exemple, si vous avez deux variables, cela équivaudra à effectuer trois régressions : une avec la variable A, une avec la variable B et une avec les deux. Cela lui permet de quantifier l’importance de chaque variable et d’appliquer cette quantification au résultat de la régression.
Résultats de la régression
Lorsque vous effectuez une régression dans Stats iq, les résultats de l’analyse contiennent les sections suivantes :
Résumé numérique
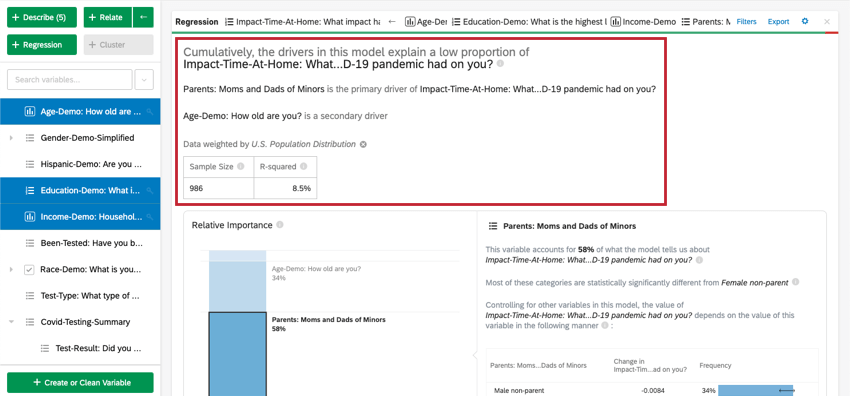
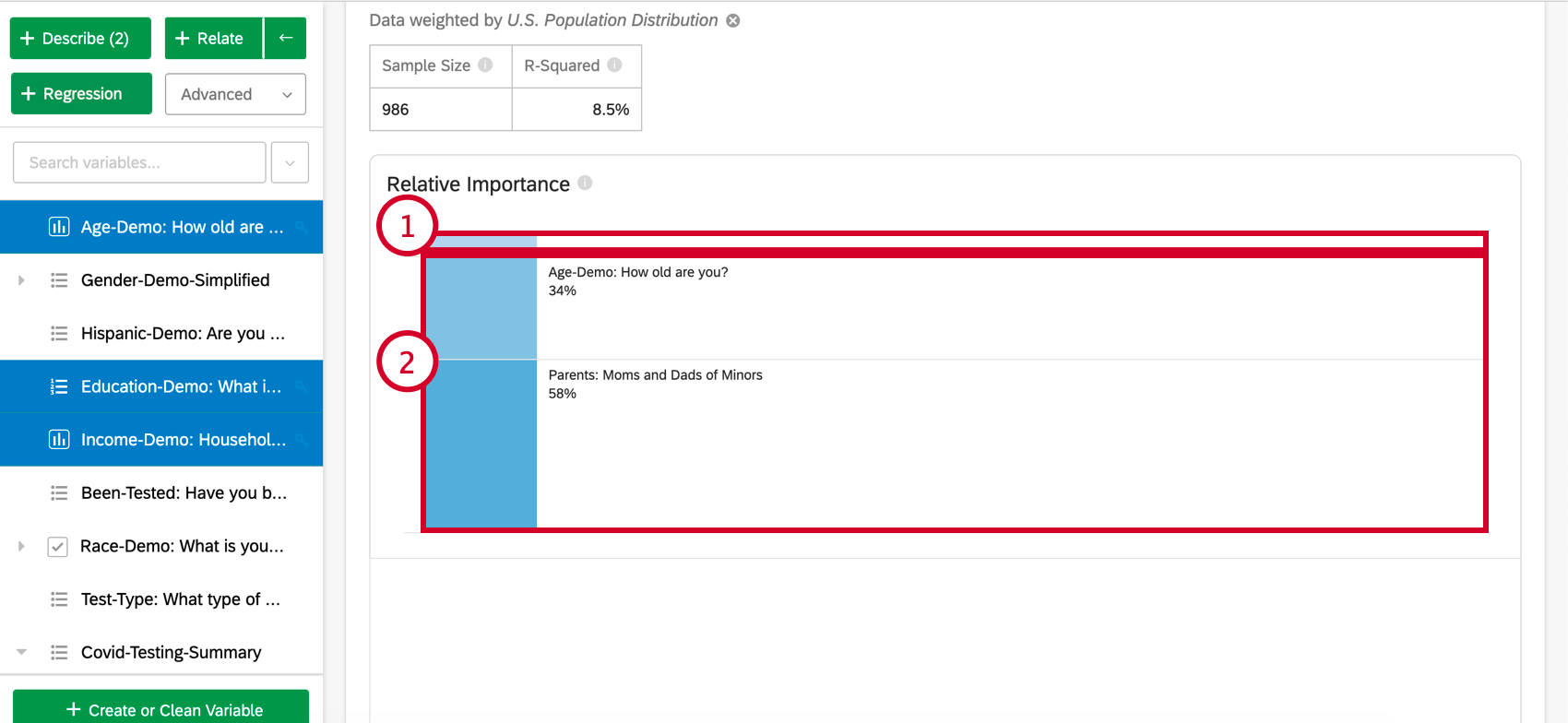
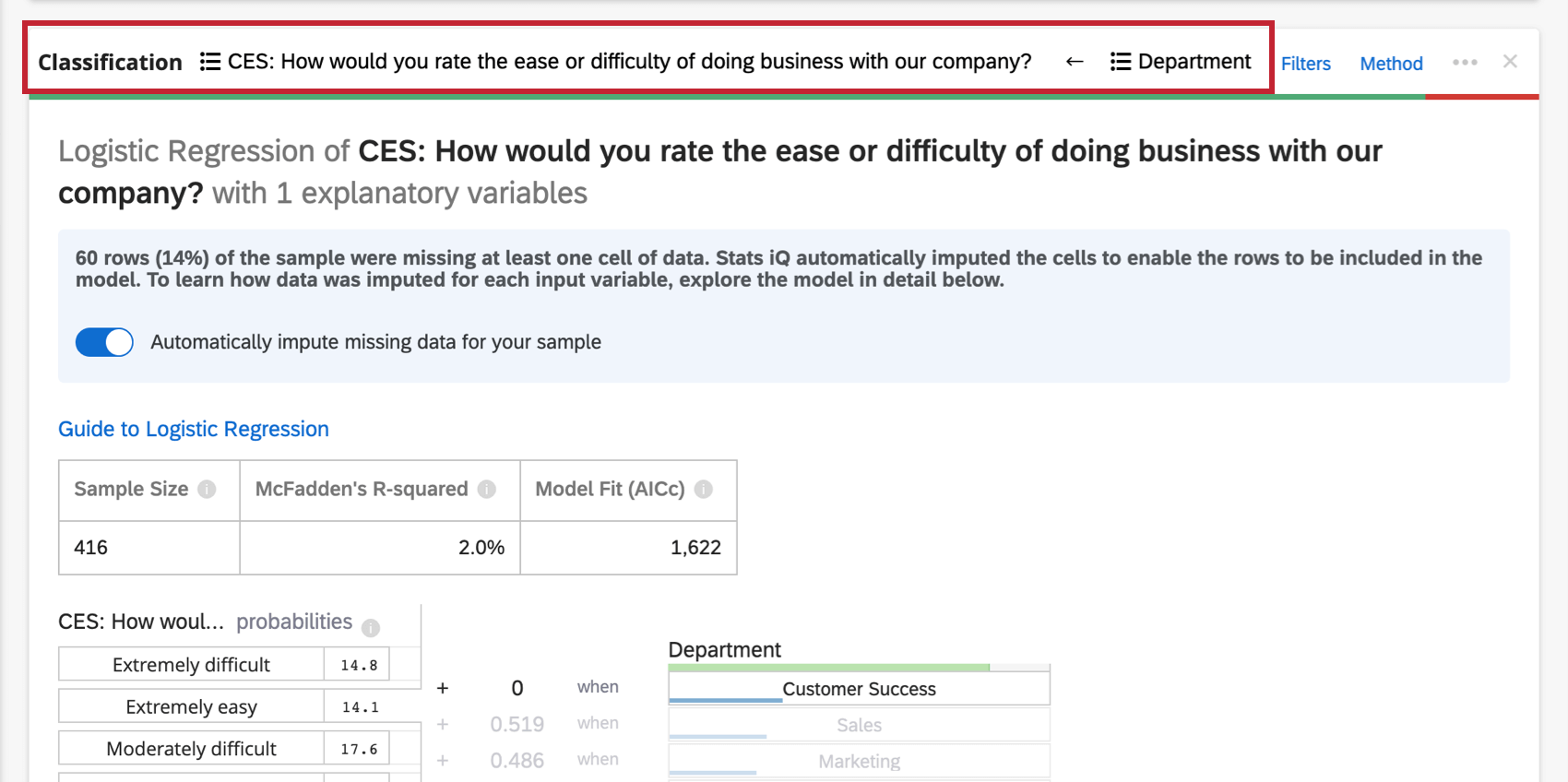
En haut de la carte figure un résumé de l’analyse de régression. En examinant les variables choisies, ce résumé écrit explique quelles variables sont les facteurs primaires et secondaires, ainsi que les facteurs qui ont eu un faible impact cumulatif. Le tableau de données comprend la taille de l’échantillon et la valeur du R au carré.
Importance relative
- Variables à faible impact: Les variables qui, individuellement, ont une importance relative de 10 % ou moins seront regroupées. Lorsqu’elle est sélectionnée, une section explique l’importance relative et la signification statistique de chaque variable à faible impact.
- Variables à fort impact: Chaque variable à fort impact sera séparée et cliquable. Une fois qu’une variable est sélectionnée, sous le diagramme à barres, vous pourrez voir la variation prise en compte et ce qui se passerait si d’autres variables étaient contrôlées dans le modèle.
Détails supplémentaires du modèle
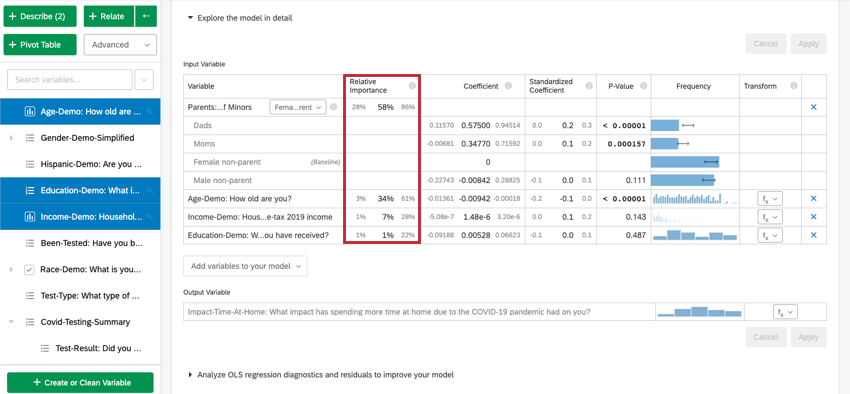
Lorsque vous sélectionnez Explorer le modèle en détail, vous verrez la liste de vos variables d’entrée et de vos variables de sortie. Vos variables d’entrée seront accompagnées des informations suivantes :
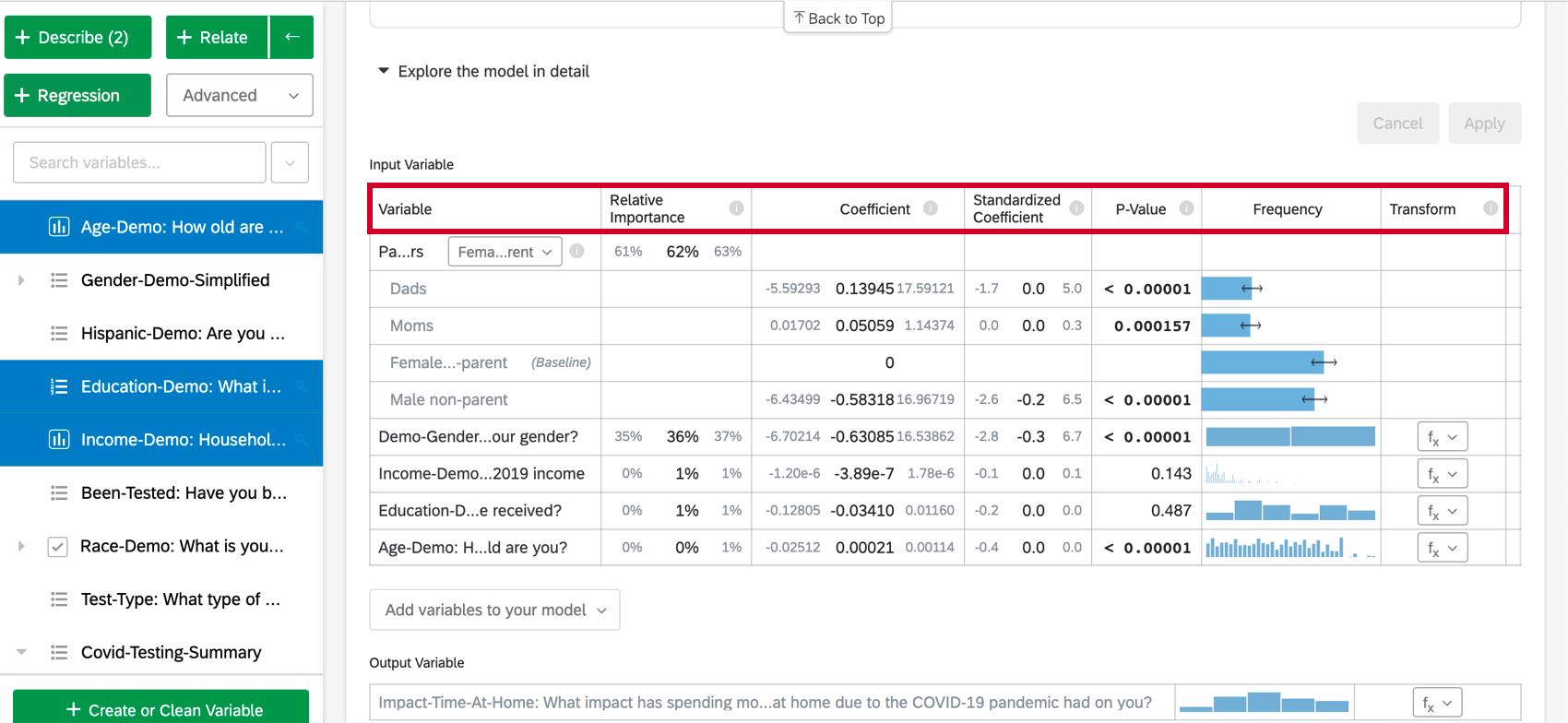
- Importance relative : La proportion du carré r qui est attribuable à une variable individuelle. Le r-carré est la proportion de la variation de la variable de résultat qui peut être expliquée par les variables d’entrée de ce modèle. Voir Importance relative pour plus de détails.
- Rapport de cotes : Ne concerne que la régression logistique. Le rapport de cotes pour une variable d’entrée donnée indique le facteur par lequel les cotes changent pour chaque unité d’augmentation de la variable explicative.
Exemple : Par exemple, si le rapport de cotes pour la satisfaction à l’égard du Manager est de 1,1 et que les groupes de la variable de sortie sont Satisfait et Non satisfait, alors pour chaque cas où la satisfaction à l’égard du Manager est supérieure de 1, les chances de la variable de sortie d’être satisfaite sont supérieures de 1,1 (10 % de plus). Si la ligne de données est une catégorie, comme color[blue], le coefficient représente le changement dans les chances de la variable de réponse si la variable Catégories est cette catégorie particulière (bleu) au lieu du groupe “de base” (rouge, vert, etc.).
- Coefficient : Chaque augmentation d’une unité d’une variable d’entrée est associée à une augmentation du coefficient de la variable de sortie. Ces coefficients sont construits sur la base des résultats de l’analyse de l’importance relative et tiennent donc compte de la multicolinéarité. Ils ne correspondent pas aux coefficients qui résulteraient d’une régression classique par les moindres carrés ordinaires.
- Coefficient normalisé : Le coefficient standardisé est le coefficient séparé par la variance de la variable d’entrée. Chaque variable est ainsi placée sur la même échelle, ce qui permet de comparer plus directement leurs coefficients.
- Valeur P : La valeur p est la mesure de la signification statistique. Des valeurs plus faibles sont associées à une probabilité plus faible que le lien soit une coïncidence. Pour les variables catégorielles, la valeur p indique la signification statistique de la différence entre un groupe et le groupe “de base” dans la variable.
- Transformer: Voir Transformer les variables.
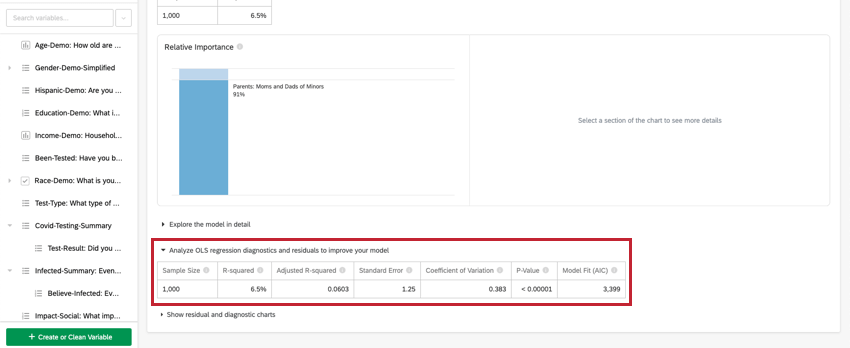
Analyse de la régression par les MCO
Pour la régression linéaire, cliquez sur Analyser les diagnostics et les résidus de la régression MCO pour améliorer votre modèle sous la variable clé/de sortie afin d’afficher les graphiques Prédit vs Réel et Résidus. Pour plus d’informations, voir Interprétation des tracés résiduels pour améliorer votre régression.
Variable incluse
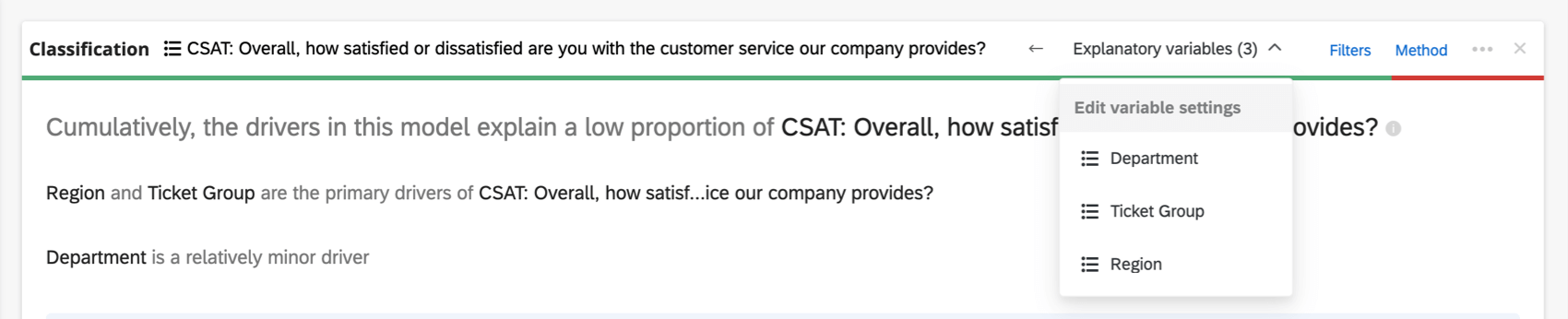
Dans l’en-tête supérieur de la carte de régression, vous verrez les variables utilisées dans la régression.
Cliquez sur le nom d’une variable pour ouvrir une nouvelle fenêtre dans laquelle vous pouvez recoder ou grouper des valeurs. Cliquez sur les flèches pour sélectionner les variables d’entrée et de sortie de l’analyse.
Si vous avez trop de variables à afficher dans l’en-tête, un menu déroulant ” Variables explicatives” vous permet de choisir les variables que vous souhaitez recoder.
Ajout et suppression de variables
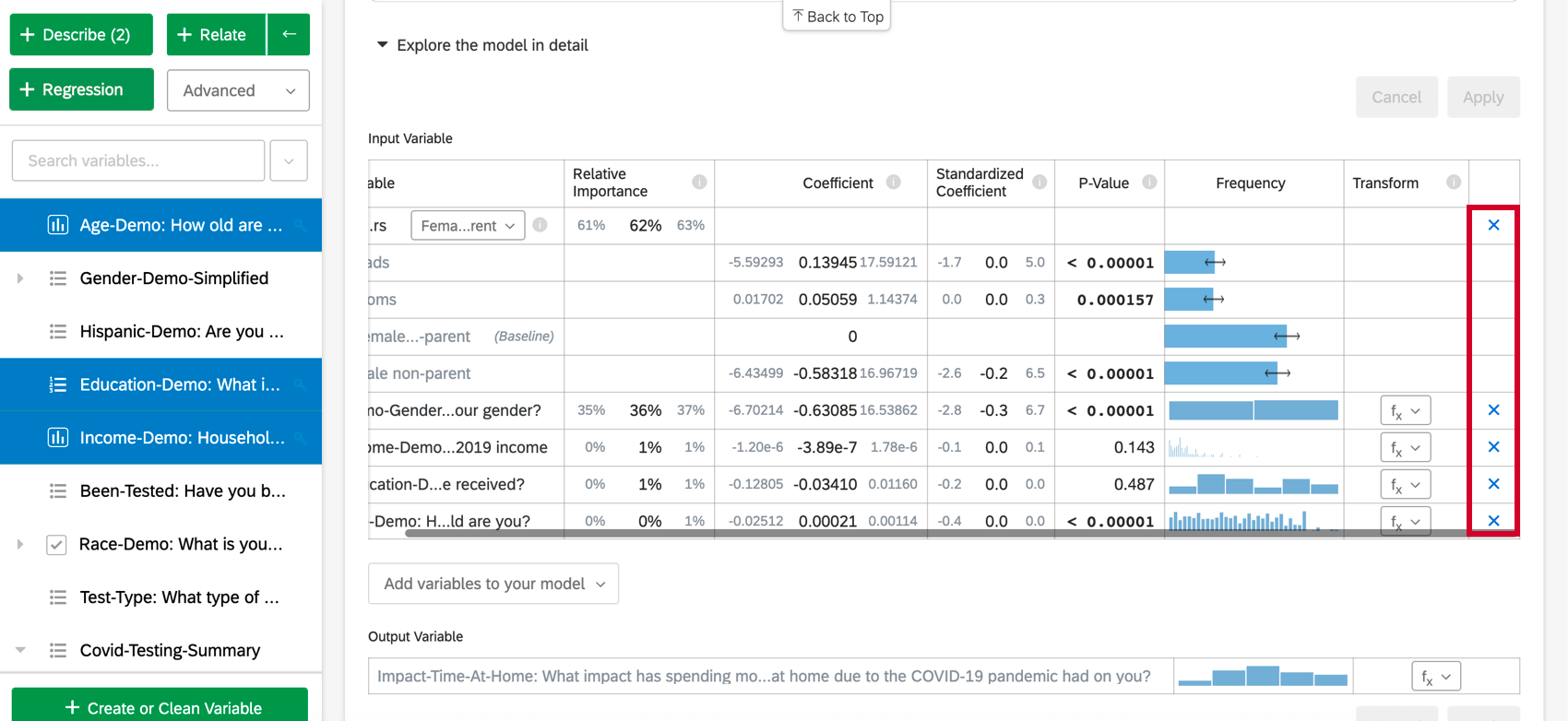
Une fois que vous avez créé une carte de régression, vous pouvez ajouter des variables supplémentaires à l’analyse en suivant les étapes ci-dessous :
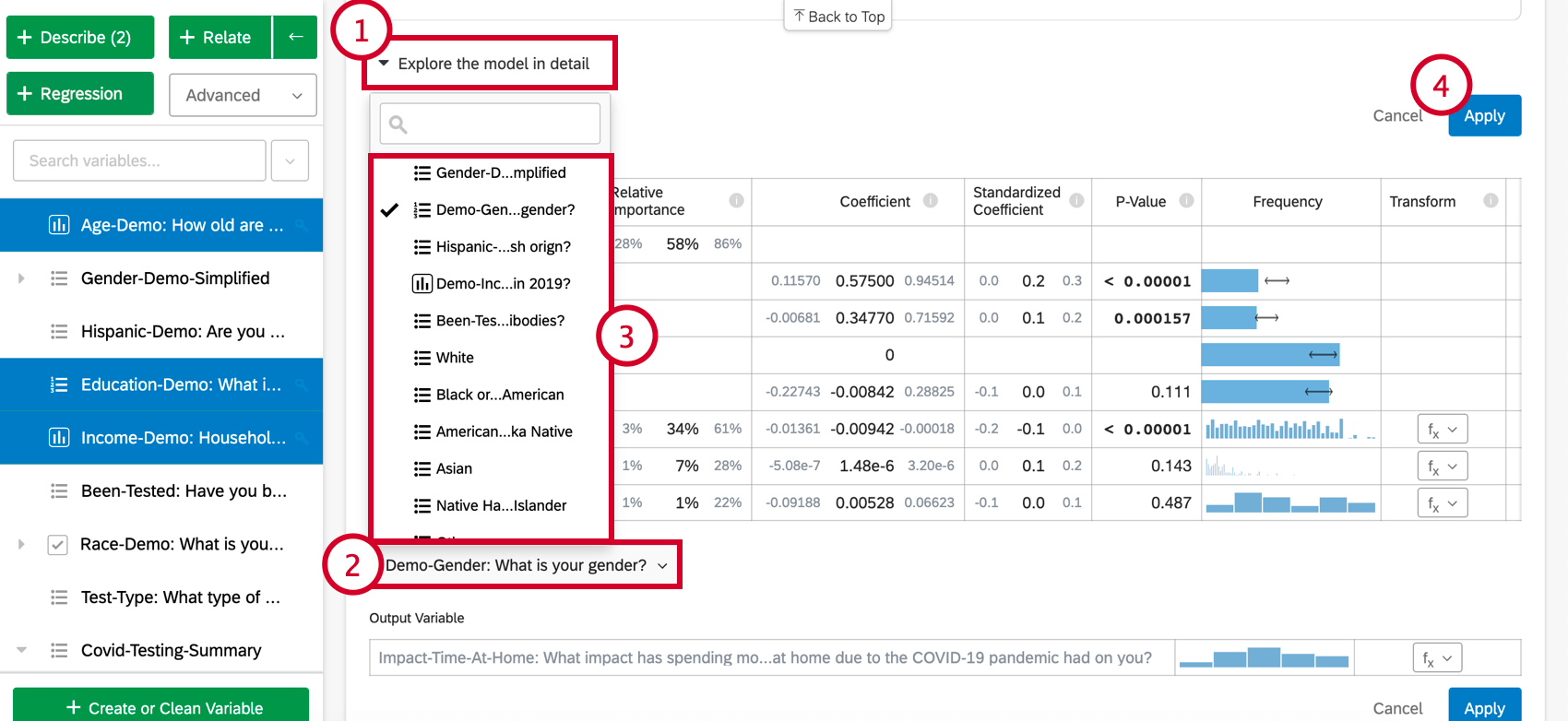
- Cliquez sur Explorer le modèle en détail.
- Sélectionnez Ajouter des variables à votre modèle au bas de la carte. La liste des variables qui n’ont pas encore été utilisées pour la régression s’affiche.
- Choisissez une variable dans cette liste.
- Cliquez sur Appliquer pour réexécuter l’analyse en tenant compte de la nouvelle variable.
Pour supprimer une variable de la régression, passez la souris sur la variable souhaitée et cliquez sur le X bleu à l’extrême droite du tableau. Après avoir choisi les variables à ajouter ou à supprimer, veillez à sélectionner “Appliquer” pour exécuter le nouveau modèle.
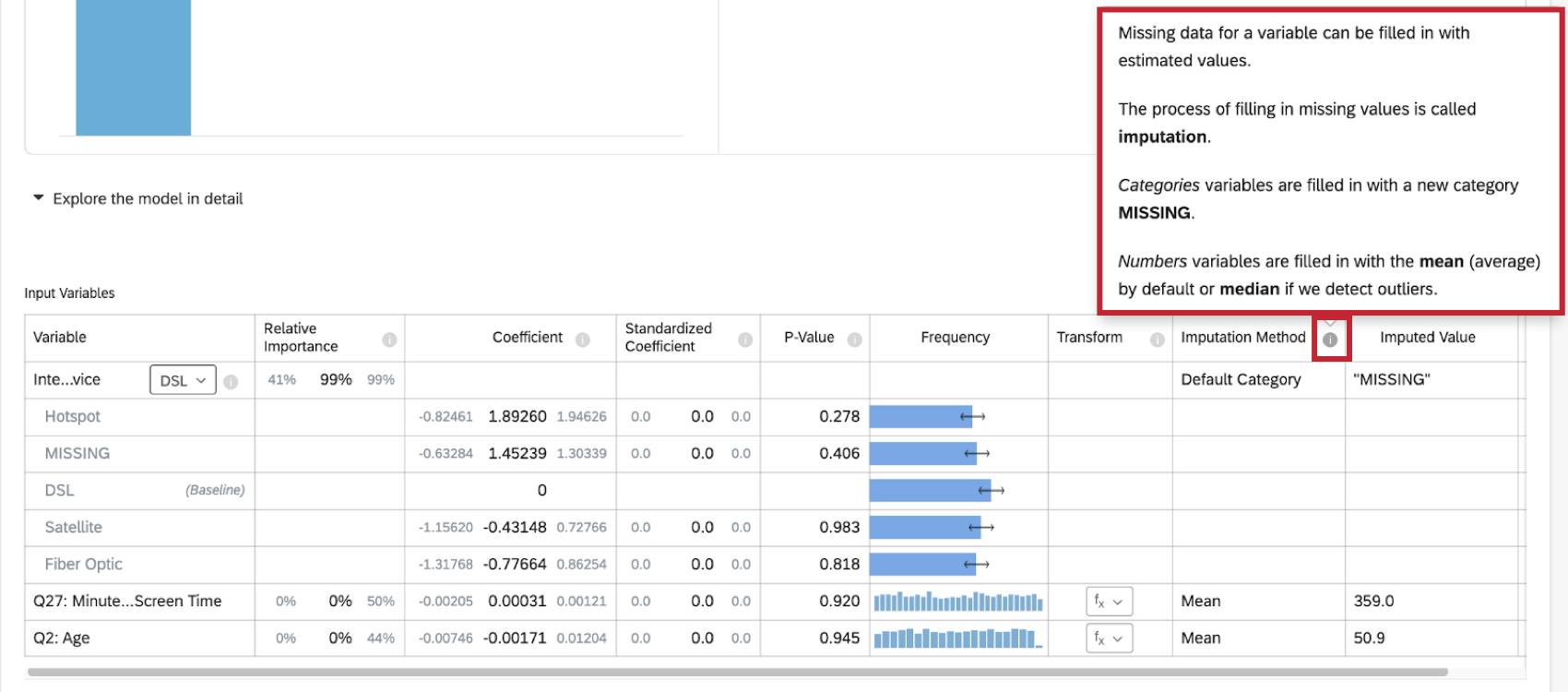
Imputer des variables
La régression ne prend en compte que les lignes où toutes les variables d’entrée sont renseignées. Cependant, la collecte de données d’enquête comporte souvent des données manquantes, ce qui peut avoir une incidence négative sur votre analyse et votre modèle de régression. Si vous n’incluez dans votre régression que les lignes pour lesquelles il n’y a pas de données manquantes, les résultats de votre analyse peuvent être faussés car votre échantillon n’est pas représentatif de l’ensemble de vos données.
Avec l’imputation, Stats iQ remplacera automatiquement les données manquantes par des valeurs estimées. Lorsque les données manquantes sont complétées, vous êtes en mesure d’inclure davantage de vos données originales dans l’analyse de régression, ce qui donne un modèle de régression moins biaisé, capable de mieux expliquer la variation de la variable de résultat souhaitée.
L’imputation est automatique. Ainsi, lorsque vous effectuez une analyse de régression sur un ensemble de données comportant des valeurs manquantes, votre ensemble de données sera imputé avant tout calcul.
- Cliquez ici pour voir un exemple de données avant et après l’imputation des variables.
- Avant l’imputation :
pour cette régression, l'”utilisation des données” est la variable de résultat et l'”âge”, le “service Internet” et les “minutes de temps d’écran” sont les variables d’entrée.ID de ligne Utilisation des données Âge Service Internet Temps d’écran (Chronomètres) 1 75 39 Satellite 503 2 19 41 Fibre optique 52 3 87 434 4 54 23 Satellite 5 14 101 6 75 Satellite 7 81 57 DSL 329 Attention : Si vous exécutez une régression sans compléter les valeurs manquantes, seules les lignes 1, 2 et 7 seront incluses.Après l’imputation :
ID de ligne Utilisation des données Âge Service Internet Temps d’écran (Chronomètres) 1 75 39 Satellite 503 2 19 41 Fibre optique 52 3 87 50.9 MANQUANT 434 4 54 23 Satellite 359.0 5 14 50.9 MANQUANT 101 6 75 50.9 Satellite 359.0 7 81 57 DSL 329 Astuce : “Service Internet” est une variable catégorielle et non numérique, la valeur manquante est donc remplie par “MISSING”.
Méthodes d’imputation
Stats iQ utilise actuellement les méthodes d’imputation suivantes :
- Catégorie par défaut: Stats iQ créera une nouvelle valeur de catégorie “MISSING” pour compléter les données manquantes. Cette méthode est utilisée pour les variables catégorielles.
- Moyenne: Si Stats iQ ne détecte aucune valeur aberrante dans la distribution de la variable numérique, les données manquantes de la variable sont complétées par la valeur moyenne. Cette méthode est utilisée pour les variables numériques.
- Médiane: Si Stats iQ détecte des valeurs aberrantes dans la distribution de la variable numérique, les données manquantes de la variable sont complétées par la valeur médiane. Cette méthode est utilisée pour les variables numériques.
Indicateurs d’imputation
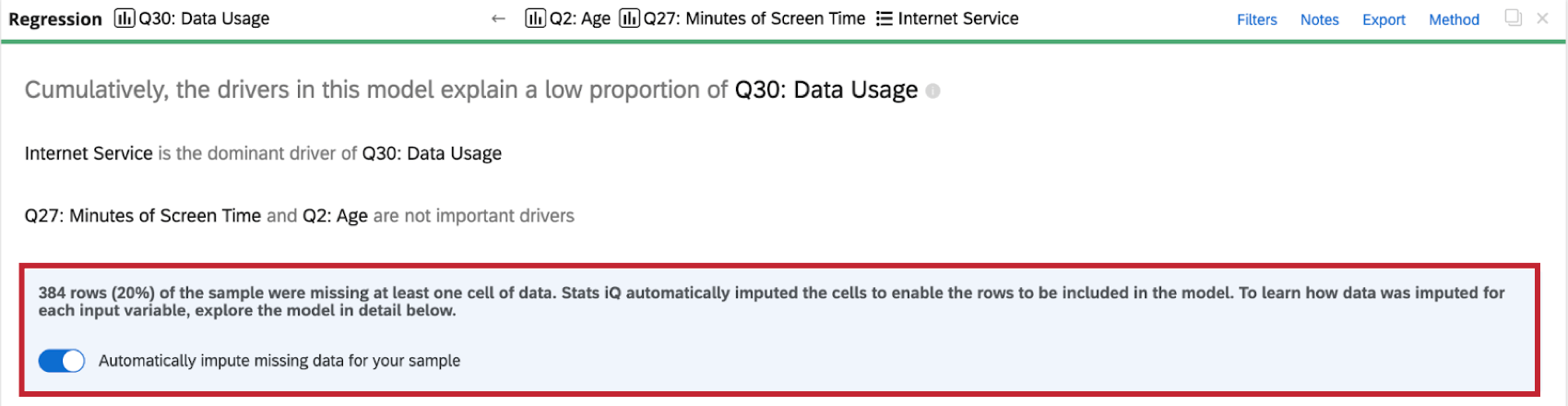
Lorsque vous effectuez une analyse de régression sur l’ensemble de données, vous verrez un indicateur d’imputation en haut de la carte de régression.
De plus amples informations sur l’imputation sont disponibles en cliquant sur le symbole d’information ( i ) suivant la méthode d’imputation.
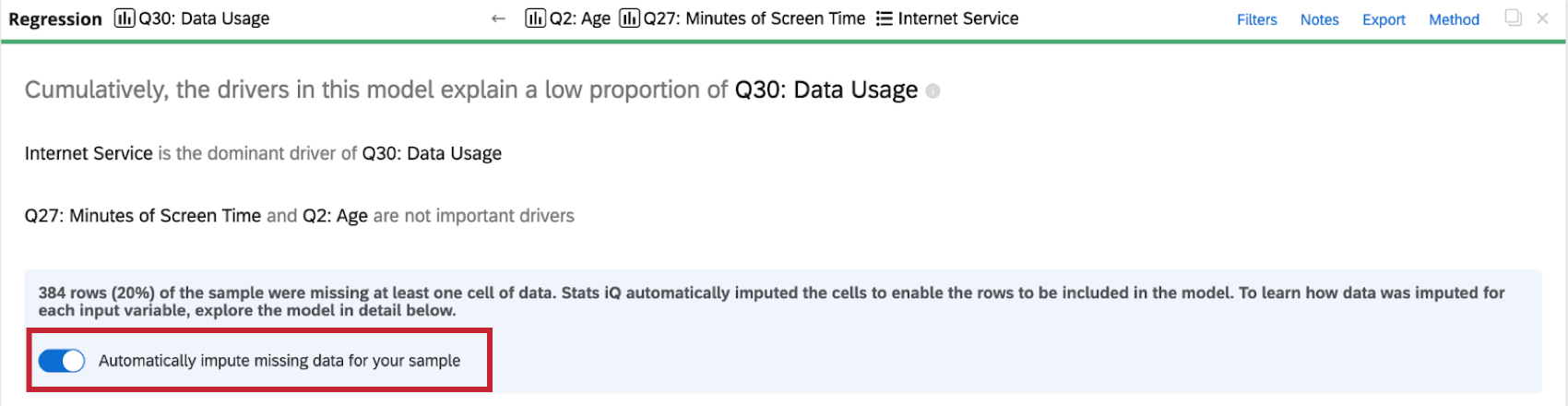
Désactiver l’imputation
Stats iQ applique automatiquement l’imputation à toutes les cartes de régression. Pour désactiver l’imputation automatique, cliquez sur Imputer automatiquement les données manquantes pour votre échantillon en haut de la carte de régression.
Avertissements relatifs à l’imputation
- Si trop de données sont imputées, votre modèle de régression sera biaisé et peu fiable. Lorsque plus de 50 % de votre ensemble de données a été rempli, Stats iQ vous avertit de ne pas tirer de conclusions à partir de vos résultats de régression.

- Lorsque des valeurs aberrantes sont détectées dans l’une des variables d’entrée numériques, Stats iQ impute les variables en utilisant la valeur médiane au lieu de la moyenne. Dans ce cas, Stats iQ vous avertit lorsque vous explorez le modèle en détail.

Transformer des variables
Lorsque vous effectuez une analyse de régression dans Stats iq, vous pouvez constater que vous devez améliorer votre modèle. La façon la plus courante d’améliorer un modèle est de transformer une ou plusieurs variables, généralement à l’aide d’un “log” ou d’une autre transformation fonctionnelle.
La transformation d’une variable modifie la forme de sa distribution. En général, les modèles de régression fonctionnent mieux avec des distributions plus symétriques, en forme de cloche. Essayez différents types de transformations jusqu’à ce que vous trouviez celle qui vous donne ce type de distribution.
Pour transformer une variable :
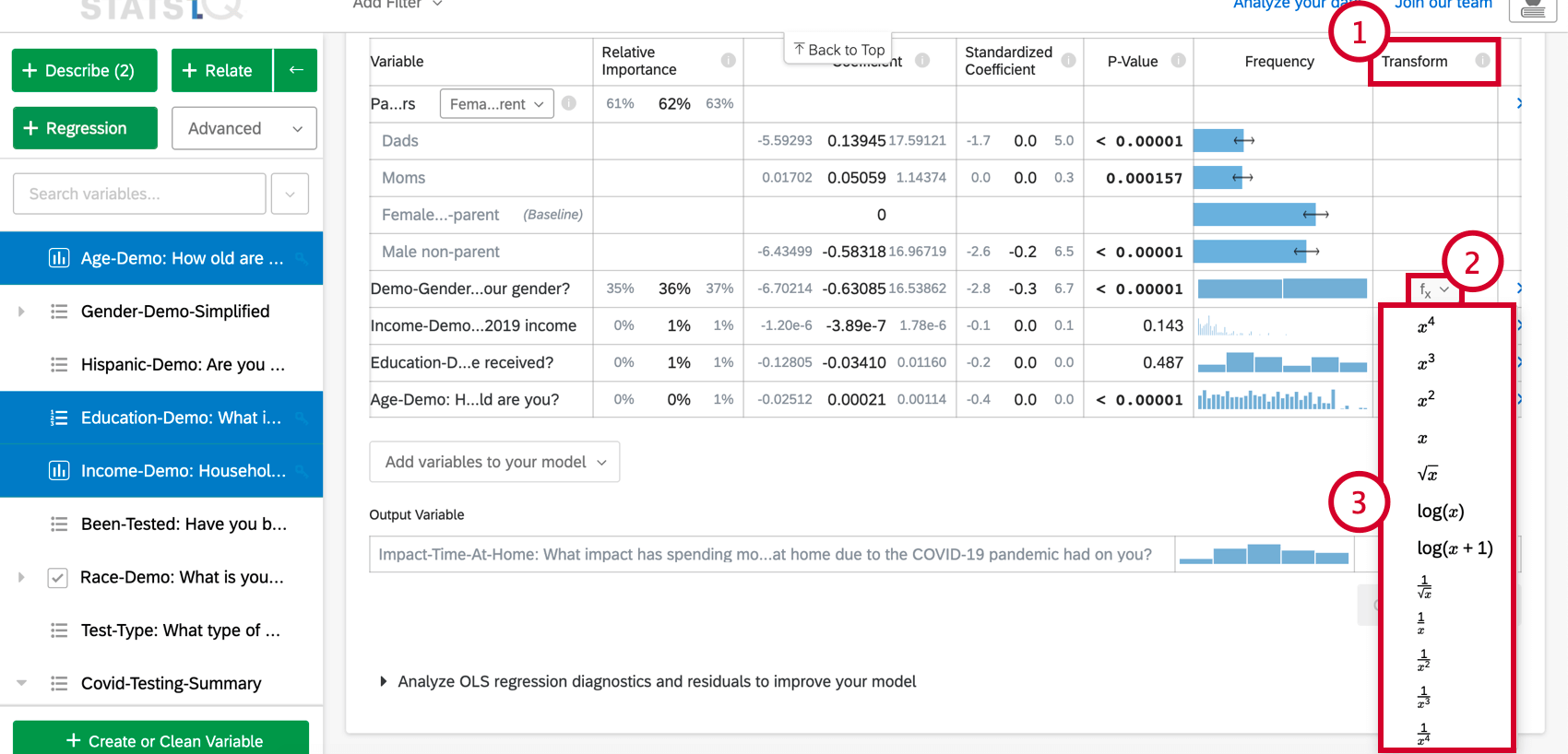
- Sous l’option Explorer le modèle en détail, faites défiler jusqu’à la colonne Transformer .
- Cliquez sur le bouton de la fonction(f(x)) correspondant à la variable que vous souhaitez transformer.
- Dans la liste, choisissez la fonction que vous souhaitez appliquer et Stats iQ recalculera la carte en utilisant la nouvelle variable transformée.
Les transformations suivantes sont disponibles dans Stats iQ :
La transformation la plus courante est de loin le log(x). Elle transforme une distribution “puissante” (comme la taille de la population d’une ville) qui comporte de nombreuses petites valeurs et un petit nombre de grandes valeurs en une “distribution normale” en forme de cloche (comme la taille) où la plupart des valeurs sont clusterisées vers le milieu.
Utilisez log(x+1) si la variable à transformer a quelques valeurs de zéro, puisque log(x) ne peut pas être calculé lorsque x est zéro.
Pour plus de détails sur la transformation des variables, voir Interprétation des diagrammes de résidus pour améliorer votre régression linéaire
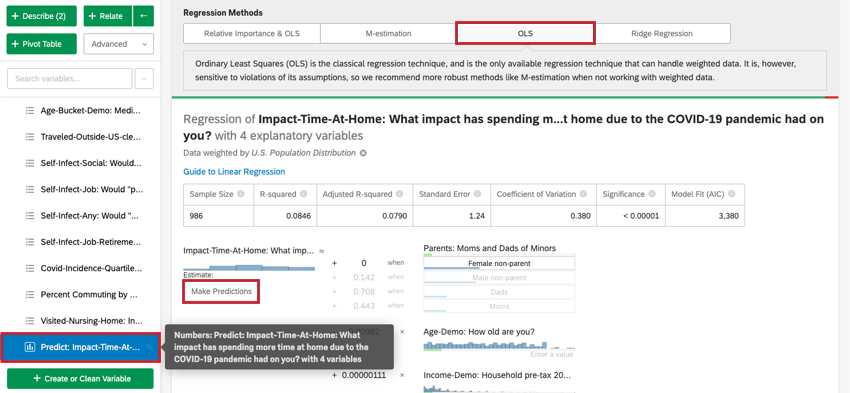
Autres techniques de régression linéaire disponibles dans Stats iQ
L’importance relative combinée aux moindres carrés ordinaires est le résultat par défaut d’une régression linéaire. Il existe cependant d’autres options.
Pour accéder à la M-estimation, aux moindres carrés ordinaires et à la régression Ridge, cliquez sur la roue dentée des paramètres dans le coin supérieur droit de votre carte de régression. En cliquant sur le nom de la technique de régression sous Méthodes de régression , vous pourrez modifier la technique de régression utilisée pour la carte de régression. Cela n’est possible que pour la régression linéaire.

- M-estimation: Conçue pour traiter les valeurs aberrantes de la variable de sortie mieux que les moindres carrés ordinaires (MCO).
- Moindres carrés ordinaires: Les moindres carrés ordinaires (MCO) sont la technique de régression classique. La Technologie est sensible aux valeurs aberrantes et aux autres violations de ses hypothèses, c’est pourquoi nous recommandons des méthodes plus robustes comme la M-estimation. Étant donné que les MCO sont utilisés dans la sortie par défaut de l’importance relative, vous ne devez sélectionner cette option que si vous êtes intéressé par les fonctions qui n’ont pas encore été adaptées à la sortie de l’importance relative : la prédiction des résultats et l’ajout de termes d’interaction.
- Régression de la crête: La régression ridge est une technique similaire à la régression standard par les MCO, mais avec un paramètre d’accord alpha. Ce paramètre alpha permet de faire face à une variance élevée et à des données souffrant de multicolinéarité. Lorsqu’elle est bien réglée, la régression ridge donne généralement de meilleures prédictions que les MCO grâce à un meilleur compromis entre le biais et la variance. Dans Stats iQ, vous pourrez choisir le paramètre alpha lors de l’utilisation de la régression ridge.
Une fois que vous avez sélectionné l’estimation M, les moindres carrés ordinaires ou la régression Ridge, vous pouvez voir les résultats. Le résultat apparaît sous la section Méthodes de régression.
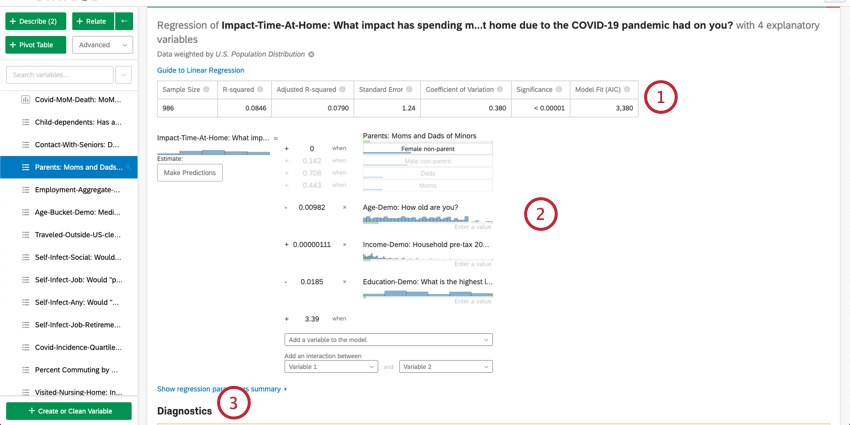
- Résumé numérique: en haut de la carte se trouve un résumé de l’analyse de régression. Il s’agit de la taille de l’échantillon, des cas manquants, de la méthode, de la valeur R au carré, de l’erreur type, du coefficient de variation et de l’adéquation du modèle.
- Détails du coefficient: Les premiers résultats de la régression, l’équation mathématique, se trouvent sous le résumé. La sortie/la variable clé se trouve à gauche de l’équation. Les variables d’entrée se trouvent sur la côte à côte. Le survol d’une variable affiche une infobulle qui explique en termes clairs comment cette variable contribue à la variable de sortie. Ici, vous pouvez également saisir des valeurs dans l’équation mathématique pour estimer les valeurs de votre variable de sortie. Pour plus d’informations, voir la section ci-dessous sur l’estimation des valeurs des variables de sortie.
- Diagnostics et résidus: Stats iQ propose des diagnostics pour vous aider à évaluer la précision et la validité de votre modèle. Pour en savoir plus, voir Interprétation des diagrammes de résidus pour améliorer votre régression linéaire ou La matrice de confusion et le compromis précision-rappel dans la régression logistique.
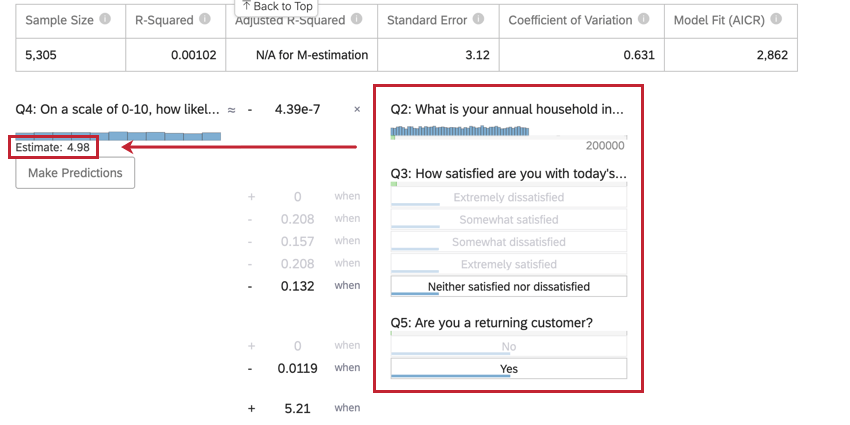
Estimation des valeurs des variables de sortie
Une fois que vous avez effectué une régression, vous pouvez utiliser l’équation mathématique dans la section Détails du coefficient pour estimer les valeurs des variables de sortie en fonction des valeurs d’entrée que vous avez sélectionnées. Sur la côte à côte de l’équation, vous verrez vos variables d’entrée. Vous pouvez définir des valeurs pour chacune de vos variables d’entrée. Sur la côte à côte de l’équation se trouve votre variable de sortie. Après avoir saisi les valeurs de vos variables d’entrée, l’équation calculera une estimation de la variable de sortie sur la base du modèle de régression.
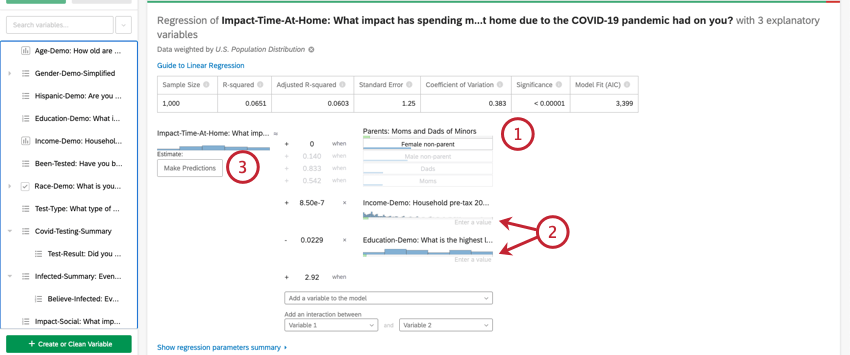
- Cette variable d’entrée est une variable de type de variable de catégorie. Pour saisir une valeur pour les variables de catégorie, cliquez sur la valeur souhaitée dans la liste des options.
- Ces variables d’entrée sont des variables de type variable numérique. Pour saisir une valeur pour les variables numériques, cliquez sur Entrer une valeur et saisissez un nombre.
- Cette variable est la variable de sortie de votre équation de régression. Après avoir sélectionné les valeurs de vos variables d’entrée, une valeur estimée pour votre variable de sortie apparaîtra suivant l’information ” Estimate”.
Prévoir les résultats
En général, vous utiliserez l’analyse de régression dans Stats iq pour comprendre le lien entre les variables d’entrée et les variables de sortie. Cependant, une fois qu’un modèle de régression est créé, il peut également être utilisé pour prédire la valeur de sortie pour les lignes de données pour lesquelles vous disposez de valeurs pour les entrées.
Conditions d’interaction et autres préoccupations avancées
Ajout de termes d’interaction
Lorsque vous cherchez à améliorer votre modèle de régression, vous pouvez ajouter des termes d’interaction en plus des variables d’entrée existantes. Un terme d’interaction sera ajouté si vous pensez que la valeur de l’une des variables d’entrée modifie la façon dont une autre variable d’entrée affecte la variable de sortie.
Par exemple, il se peut que les jeunes soient plus satisfaits que les personnes plus âgées lorsqu’ils ont des enfants présents lors d’un séjour à l’hôtel, mais qu’ils soient moins satisfaits lorsqu’ils n’ont pas d’enfants présents. Cela signifie qu’il y a une interaction entre “Enfants présents” et “Âge”
La sélection de deux variables sous Ajouter une interaction entre en bas de la liste des variables d’entrée de la carte permet d’ajouter un terme d’interaction à la régression. Cette fonctionnalité n’est disponible que pour les moindres carrés ordinaires, l’estimation M et la régression Ridge.
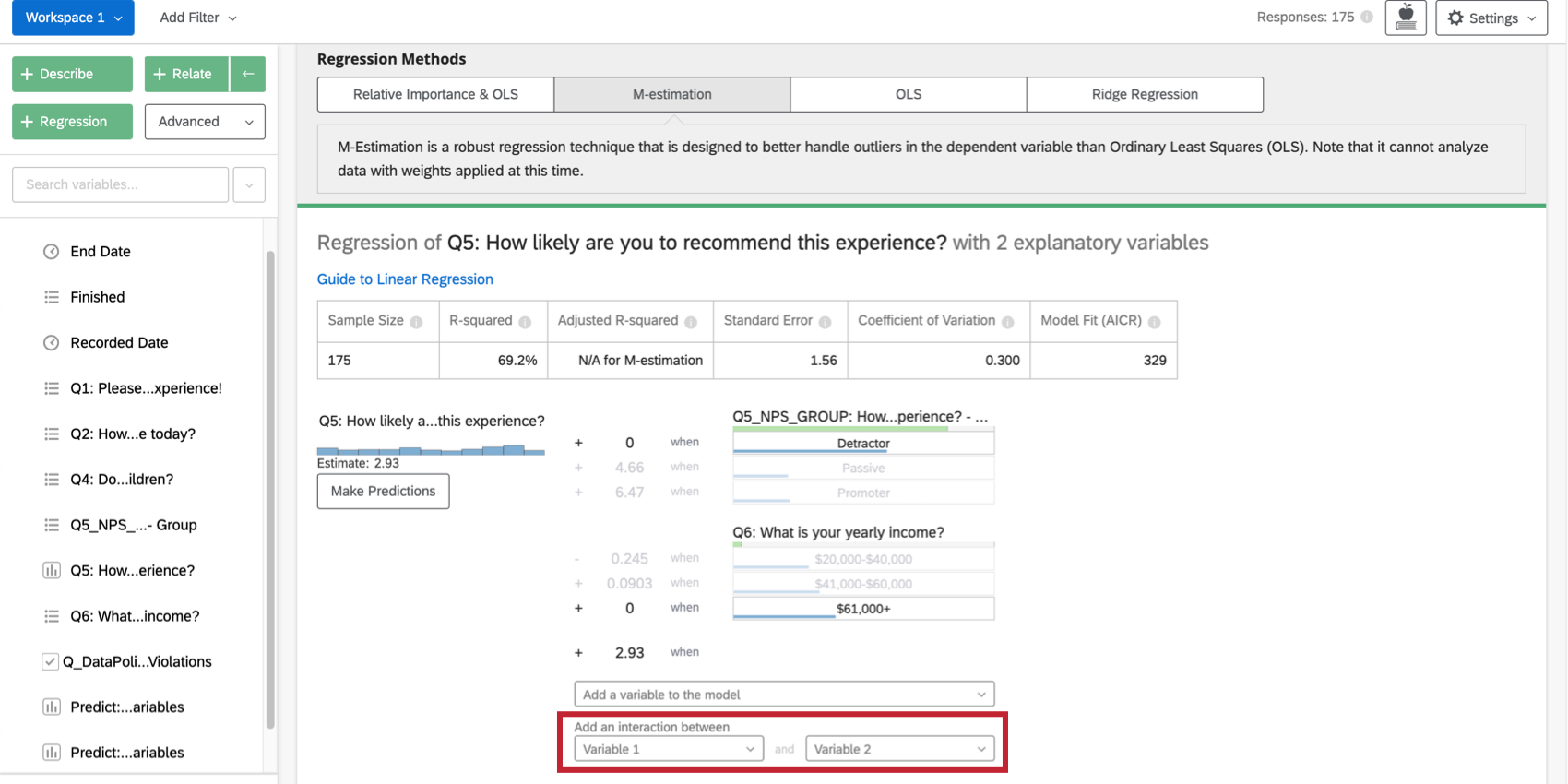
Vous pouvez obtenir le même effet pour les variables catégorielles dans une analyse d’importance relative en créant une nouvelle variable qui combine les deux. Par exemple, vous pouvez combiner la variable Couleur (avec les groupes rouge et vert ) avec la variable Taille (avec les groupes grand et petit ) pour créer une variable appelée TailleCouleur (avec les groupes GrandRouge, GrandVert, PetitRouge et PetitVert).
Multicollinéarité
La multicolinéarité se produit dans un contexte de régression lorsque deux ou plusieurs variables d’entrée sont fortement corrélées entre elles.
Lorsque deux variables sont fortement corrélées, les mathématiques de la régression mettent généralement autant de valeur que possible dans une variable et pas dans l’autre. Cela se traduit par un coefficient plus élevé pour cette variable. Mais si le modèle est modifié, même légèrement (par l’ajout d’un filtre, par exemple), la variable dans laquelle la plus grande partie de la valeur a été placée peut changer. Cela signifie que même un petit changement peut avoir un effet radical sur le modèle de régression.
L’analyse de l’importance relative permet de résoudre ce problème sans avoir à s’en préoccuper. Si vous préférez utiliser l’une des autres méthodes et que votre modèle présente ce problème, la présence de multicolinéarité (mesurée par le “facteur d’inflation de la variance”) déclenchera un avertissement et vous suggérera de supprimer une variable ou de combiner des variables en calculant leur moyenne, par exemple.
Messages d’avertissement
Stats iQ vous avertit lorsque vos résultats de régression présentent des problèmes potentiels. Il s’agit notamment des situations suivantes :
- Les variables d’entrée de votre régression ne sont pas statistiquement significatives.
- Votre transformation a supprimé des données de la régression.
- Deux variables ou plus sont fortement corrélées entre elles et rendent vos résultats instables, c’est-à-dire qu’il y a multicollinéarité.
- Les résidus ont un profil qui suggère que le modèle pourrait être amélioré.
- Une variable n’ayant qu’une seule valeur a été automatiquement supprimée.
- La taille de l’échantillon est trop faible par rapport au nombre de variables d’entrée dans la régression.
- Une variable de catégorie avec trop d’options de réponses a été ajoutée.