Guide convivial de la régression logistique

Qu’est-ce que la régression logistique ?

La régression logistique estime une formule mathématique qui relie une ou plusieurs variables d’entrée à une variable de sortie.

Par exemple, supposons que vous gériez un stand de limonade et que vous soyez intéressé par les types de clients qui ont tendance à revenir. Vos données incluent une entrée pour chaque client, son premier achat et s’il est revenu dans le mois suivant pour plus de limonade. Vos données peuvent ressembler à ceci :

Vous pensez que “Age du client” (une variable d’entrée ou explicative) peut avoir un impact sur “Retour” (une variable de sortie ou de réponse). La régression logistique peut donner ce résultat :

À l’âge de 12 ans (l’âge le plus bas), la probabilité de retour est de 10 %.

Pour chaque année supplémentaire d’âge, “Retour” est 1,1 fois plus à “Restituer”.

Cette connaissance est utile pour deux raisons.

Tout d’abord, il vous permet de comprendre une relation : les clients plus âgés sont plus susceptibles de revenir. Cette visibilité peut vous amener à plier votre publicité à l’égard de clients plus âgés, car ils seront plus susceptibles de devenir des clients récurrents.

Ensuite, et en relation, il peut également vous aider à faire des prédictions spécifiques. Si un client de 24 ans se débrouille, vous pourriez estimer que s’il achetait de la limonade, il y a 26 % de chances qu’il devienne plus tard un client de retour.

Compréhension de la multiplication des cotes

Notez que si nous avons dit que “Renvoyé” était “1,5 fois plus probable” dans certaines situations que dans une autre, nous faisons ce qui suit :

Les cotes étaient de 1:9, également écrites 1/(1+9) = 10 %.

La “cote pour” (le 1) est multipliée par 1,5.

Maintenant 1,5:9, écrit également 1,5/(1,5+9) = 14%.

Autre exemple, cette fois de passer de 50 % de probabilité à quelque chose de 3 fois plus probable :

Les cotes étaient de 1:1, également écrites 1/(1+1) = 50 %.

Les “cotes pour” (le côté gauche 1) sont multipliées par 3.

Maintenant 3:1, écrit également 3/(3+1) = 75%.

Nous allons maintenant suivre le processus de création de ce modèle de régression.

Préparation à la création d’un modèle de régression

1. Réfléchissez à la théorie de votre régression.

Une fois que vous avez sélectionné une variable de réponse, « Chiffre d’affaires » émet l‘hypothèse selon laquelle différentes entrées peuvent y être liées. Par exemple, vous pourriez penser qu’une température plus élevée au premier achat entraînera une probabilité plus élevée de “Retourné”, vous n’êtes peut-être pas sûr de l’impact de “l’âge” sur “Retour“, et vous pouvez croire que “Pantalons” (vs. short) est affecté par “Température” mais n’a aucun impact sur votre stand de limonade.

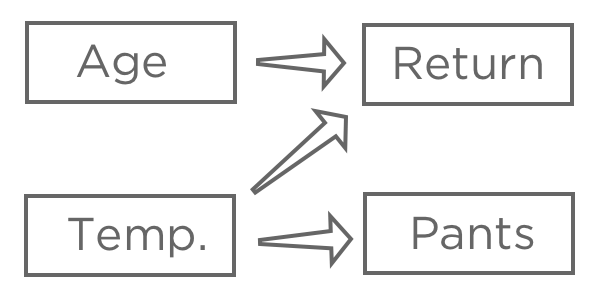
L’objectif de la régression est généralement de comprendre la relation entre plusieurs entrées et une sortie, donc dans ce cas vous décideriez probablement de créer un modèle expliquant “Retour” avec “Température” et “Age” (dit aussi “prédire le retour de la température et de l’âge”, même si vous êtes plus intéressé par l’explication que par la prédiction réelle).

Vous n’incluez probablement pas « Pantalon » dans votre régression. Il peut être corrélé avec “Retour” car les deux sont liés à la “Température”, mais il ne vient pas avant “Retour” dans la chaîne causale, de sorte que l’inclusion de ce dernier risque de dérouter votre modèle.

2. « Décrivez » toutes les variables qui pourraient être utiles pour votre modèle.

Commencez par décrire la variable de réponse, en l’occurrence « Chiffre d’affaires », et d’en avoir une bonne impression. Procédez de même pour vos variables explicatives.

Note qui ont une forme comme celle-ci…

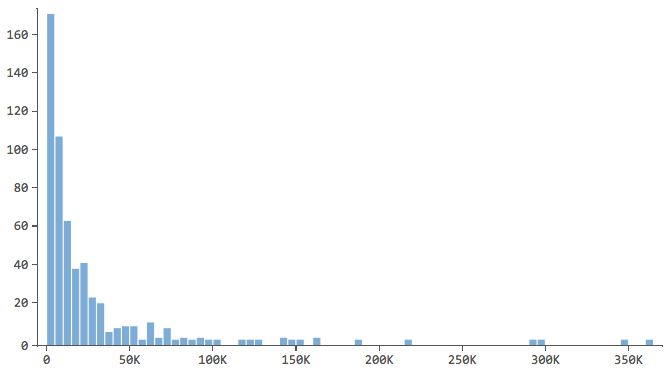
… où la plupart des données se trouvent dans les premières classes de l’histogramme. Ces variables nécessiteront une attention particulière ultérieurement.

3. « Relier » toutes les variables explicatives possibles à la variable de réponse.

Stats iQ trie les résultats en fonction de la force de la relation statistique. Jetez un œil aux résultats, en notant les variables liées au “Chiffre d’affaires” et comment.

4. Commencez à créer la régression.

La construction d’un modèle de régression est un processus itératif. Vous exécuterez les trois étapes suivantes autant de fois que nécessaire.

Les trois étapes de la création d’un modèle de régression

Étape 1 : ajouter ou soustraire une variable.

Un par un, commencez à ajouter dans les variables que vos analyses précédentes indiquées étaient liées au “Revenu des ventes” (ou ajoutez en variables que vous avez une raison théorique d’ajouter). Parvenir un par un n’est pas absolument nécessaire, mais cela facilite l’identification et la résolution des problèmes au fur et à mesure et vous aide à vous familiariser avec le modèle.

Supposons que vous commenciez par prédire “Chiffre d’affaires” avec “Température”. Vous trouvez une relation forte, vous évaluez le modèle et vous le trouvez satisfaisant (plus de détails en une minute).

Retour <– Température

Vous ajoutez ensuite dans “Lemonade color” et maintenant votre modèle de régression comporte deux termes, qui sont tous deux des prédicteurs statistiquement significatifs. Comme ceci :

Chiffre d’affaires <– Température et Lemonade

Ensuite, vous ajoutez “Sexe”, et les résultats du modèle montrent maintenant que “Sexe” est statistiquement significatif dans le modèle, mais “Lemonade color” ne l’est plus. Généralement, vous supprimez “Lemonade color” du modèle. Voici à présent :

Chiffre d’affaires <– Température et sexe

En d’autres termes, si vous connaissez le sexe du client, savoir quelle couleur de limonade il a commandé ne vous donne pas plus d’informations sur le fait qu’il sera un client de retour.

Vous pourriez enquêter et découvrir que les femmes ont tendance à choisir la limonade jaune plus que les hommes et que les femmes sont plus susceptibles de revenir. Il est donc apparu initialement que le choix du jaune rendait un client plus susceptible de revenir, mais en fait, “Lemonade color” n’est lié qu’à “Return” par “Sex“. Ainsi, lorsque vous incluez “Sexe” dans la régression, “Lemonade color” sort de la régression.

Interpréter les résultats de régression prend beaucoup de jugement, et simplement parce qu’une variable est statistiquement significative, ne signifie pas qu’elle est réellement causale. Mais en ajoutant et soustrayant soigneusement des variables, en notant comment le modèle change et en pensant toujours à la théorie sous-jacente à votre modèle, vous pouvez déchirer les relations intéressantes dans vos données.

Étape 2 : Évaluez le modèle.

Chaque fois que vous ajoutez ou soustrayez une variable, vous devez évaluer la précision du modèle en regardant son coefficient de détermination (^R2), son AICc et toute alerte de Stats iQ. Chaque fois que vous modifiez le modèle, comparez les nouveaux tracés R², AICc et diagnostique aux anciens afin de déterminer si le modèle s’est amélioré ou non.

R au carré (^R2)

La métrique numérique permettant de quantifier la précision des prévisions du modèle est connue sous le nom de coefficient de détermination (R²), qui se situe entre zéro et un. Un zéro signifie que le modèle n’a pas de valeur prédictive et qu’un seul signifie que le modèle prédit parfaitement tout.

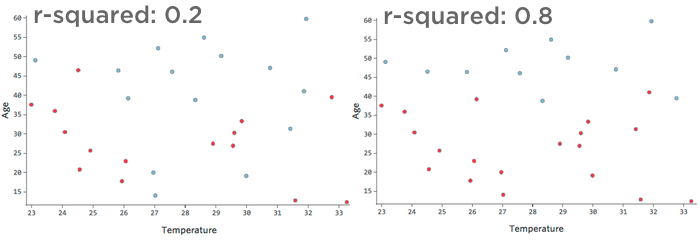
Par exemple, les données représentées à gauche conduiront à un modèle beaucoup moins précis que les données de droite. Imaginez tenter de tracer une ligne à travers le nuage de points ; vous pourriez presque complètement séparer le bleu (“Renvoyé”) du rouge (“Didn’t”) sur le côté droit, mais sur le côté gauche, ce serait dur de le faire.

Autrement dit, le côté droit a un coefficient de détermination élevé ; si vous connaissez “Température” et “Age”, vous pouvez déterminer “Retourné” vs. « C’est pas facile ». Le côté gauche a un coefficient de détermination inférieur à moyen ; si vous connaissez “Température” et “Age”, vous avez une assez bonne supposition quant à savoir si elle sera “Retourné” vs. “Non”, mais il y aura beaucoup d’erreurs.

Il n’existe pas de définition fixe d’un « bon » coefficient de détermination. Dans certaines options, il peut être intéressant de voir n’importe quel effet, tandis que dans d’autres, votre modèle peut être inutile, sauf s’il est très précis.

Chaque fois que vous ajoutez une variable, le coefficient de détermination (R²) augmente. L’objectif n’est donc pas d’atteindre le coefficient de détermination le plus élevé possible. Vous voulez plutôt équilibrer la précision du modèle (R²) avec sa complexité (en général, le nombre de variables qu’il contient).

AIC

AICc est une métrique qui équilibre la précision et la complexité. Une plus grande précision conduit à de meilleurs scores et une complexité accrue (plus de variables) conduit à des scores moins bons. Le modèle avec l’AICc inférieur est meilleur.

Notez que la métrique AICc n’est utile que pour comparer les AICcs de modèles qui ont le même nombre de lignes de données et la même variable de sortie.

Alertes

De temps à autre, Stats iQ vous suggérera des moyens d’améliorer votre modèle. Par exemple, Stats iQ peut suggérer que vous preniez le logarithme d’une variable (détails sur ce que cela signifie).

Matrice de confusion et courbe de rappel de précision

La matrice de confusion et la courbe de rappel de précision sont également des outils utiles pour comprendre la précision de votre modèle. Et si vous souhaitez faire des prévisions basées sur votre modèle, ces outils vous y aideront. Elles ne sont pas strictement nécessaires pour bien comprendre ce que votre modèle vous dit, nous les plaçons donc dans une section différente sur la matrice de confusion et la courbe de rappel de précision.

Étape 3 : Modifiez le modèle en conséquence.

Si votre évaluation du modèle a révélé qu’il était satisfaisant, soit vous avez terminé, soit vous pouvez revenir à la phase 1 et saisir plus de variables.

Si votre évaluation révèle que le modèle manque, vous utiliserez les alertes de Stats iQ pour résoudre les problèmes.

Lorsque vous modifiez le modèle, notez continuellement les changements de R², AICR et diagnostics résiduels, et décidez si les modifications que vous apportez aident ou nuisent à votre modèle.

FAQ