Guide convivial de la régression linéaire

Qu’est-ce que la régression ?

La régression estime une formule mathématique qui relie une ou plusieurs variables d’entrée à une variable de sortie.

Par exemple, supposons que vous gériez un stand de limonade et que vous soyez intéressé par ce qui génère du chiffre d’affaires. Vos données incluent le chiffre d’affaires de chaque jour, la température élevée, le nombre d’enfants qui ont marché, le nombre d’adultes qui ont marché, ce que vous avez utilisé ce jour-là, et un chiffre d’affaires du concurrent à proximité.

Vous pensez que “Température” (une variable d’entrée ou une variable explicative) peut avoir un impact sur “Chiffre d’affaires” (une variable de sortie ou de réponse). Lorsque vous utilisez la régression pour analyser cette relation, elle peut donner cette formule :

Chiffre d’affaires = 2,71 * Température   –   35Cette

formule est utile pour deux raisons.

Tout d’abord, il vous permet de comprendre une relation : des jours plus chauds conduisent à plus de “Revenu”. En particulier, le 2,71 avant “Température” (appelé le coefficient) signifie que pour chaque degré “Température” monte, en moyenne il y aura 2,71$ de plus “Revenu”. Cette intuition peut vous amener à décider de ne pas vendre de limonade les jours froids.

Ensuite, et en relation, il peut également vous aider à faire des prédictions spécifiques. Si la “Température” est 24, vous pouvez estimer que depuis…

Chiffre d’affaires = 2,71 * Température   –   35
Chiffre d’affaires = 2,71 * 24   –   35
Chiffre d’affaires = 30

…vous aurez environ 30 $ en “Chiffre d’affaires”. Cela peut être utile pour savoir si vous serez en mesure d’effectuer un paiement ce jour-là, en supposant que vous êtes certain que votre modèle est précis.

Nous allons maintenant suivre le processus de création de cette équation de régression.

Préparation à la création d’un modèle de régression

1. Réfléchissez à la théorie de votre régression

Une fois que vous avez choisi une variable de réponse, « Revenu des ventes », imaginez comment les différentes entrées peuvent y être liées. Par exemple, vous pourriez penser qu’une « température » plus élevée entraînera une augmentation du « chiffre d’affaires », vous n’êtes peut-être pas sûr de l’impact de différentes signatures sur le « chiffre d’affaires », et vous pourriez croire que les « ventes du concurrent » sont affectées par la « température » mais n’ont aucun impact sur votre stand de limonade.

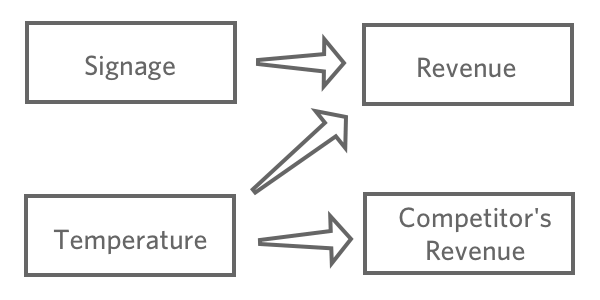
L’objectif de la régression est généralement de comprendre la relation entre plusieurs entrées et une sortie, donc dans ce cas, vous décideriez probablement de créer un modèle expliquant “Chiffre d’affaires” avec “Température” et “Signalisation” (également dit comme “prédire le revenu de la température et de la signalisation“, même si vous êtes plus intéressé par l’explication que la prédiction réelle).

Vous n’incluez probablement pas les « ventes du concurrent » dans votre régression. Il est probablement corrélé avec “Chiffre d’affaires”, mais il ne vient pas avant dans la chaîne causale, de sorte que l’inclusion de ce produit risque de perturber votre modèle.

2. « Décrire » toutes les variables qui pourraient être utiles pour votre modèle

Commencez par décrire la variable de réponse, en l’occurrence “Chiffre d’affaires”, et en vous sentant bien. Procédez de même pour vos variables explicatives.

Note qui ont une forme comme celle-ci…

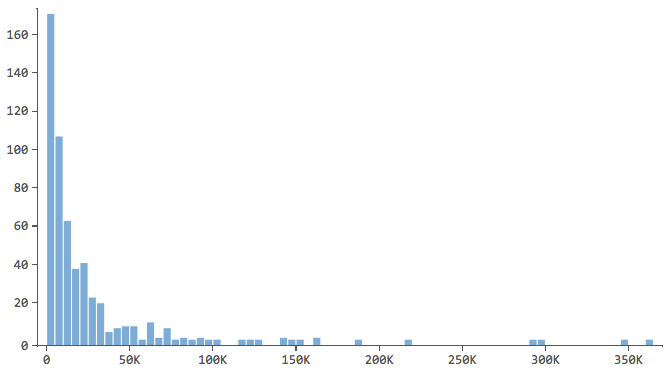
… où la plupart des données se trouvent dans les premières classes de l’histogramme. Ces variables nécessiteront une attention particulière ultérieurement.

3. « Relier » toutes les variables explicatives possibles à la variable de réponse

Stats iQ triera les résultats en fonction de la force de la relation statistique. Jetez un œil aux résultats, en notant les variables liées au “Chiffre d’affaires” et comment.

Si vous avez déjà une bonne idée des variables qui doivent théoriquement piloter l’édition (par exemple, à partir de documents universitaires précédents), vous devez ignorer cette étape. Mais si votre analyse est un peu plus exploratoire (comme une enquête client), il s’agit d’une étape utile et importante.

4. Commencez à créer la régression.

La création d’un modèle de régression est un processus itératif. Vous exécuterez les trois étapes suivantes autant de fois que nécessaire.

Les trois étapes de la création d’un modèle de régression

Étape 1 : ajouter ou soustraire une variable

Un par un, commencez à ajouter dans les variables que vos analyses précédentes indiquées étaient liées au “Revenu des ventes” (ou ajoutez en variables que vous avez une raison théorique d’ajouter). Parvenir un par un n’est pas absolument nécessaire, mais cela facilite l’identification et la résolution des problèmes au fur et à mesure et vous aide à vous familiariser avec le modèle.

Supposons que vous commenciez par prédire “Chiffre d’affaires” avec “Température”. Vous trouvez une relation forte, vous évaluez le modèle et vous le trouvez satisfaisant (plus de détails en une minute).

Chiffre d’affaires = 2,71 * Température   –   35Vous

ajoutez ensuite “Nombre d’enfants qui ont parcouru” et maintenant votre modèle de régression a deux termes, qui sont tous deux des prédicteurs statistiquement significatifs. Comme ceci :

Chiffre d’affaires = 2,5 * Température   +   0.3 * NumberOfChildrenWhoWalkedBy   –   12Puis

vous ajoutez “Nombre d’adultes qui ont marché par”, et les résultats du modèle montrent maintenant que “Nombre d’adultes” est statistiquement significatif dans le modèle, mais “Nombre d’enfants” ne l’est plus. Généralement, vous supprimez “Nombre d’enfants” du modèle. Voici à présent :

Chiffre d’affaires = 2,6 * Température   +   0,4 * NumberOfAdultsWhoWalkedBy   –   14

Cela signifie que « le nombre d’adultes » est le meilleur prédicteur du « chiffre d’affaires », c’est-à-dire que si vous savez combien d’adultes viennent, savoir combien d’enfants arrivent n’ajoute pas de nouvelles informations, cela ne vous aide pas à prévoir les ventes.

Vous vous souvenez peut-être que les enfants n’achètent jamais votre limonade, il est donc logique que cette variable n’appartienne pas au modèle.

Mais pourquoi était-ce statistiquement significatif dans le premier modèle ? Probablement parce que “Nombre d’enfants” est corrélé avec “Nombre d’adultes“, et comme “Nombre d’adultes” n’était pas encore dans le modèle, “Nombre d’enfants” agissait comme une approximation approximative du “Nombre d’adultes”.

Interpréter les résultats de régression prend beaucoup de jugement, et simplement parce qu’une variable est statistiquement significative ne signifie pas qu’elle est réellement causale. Mais en ajoutant et soustrayant soigneusement des variables, en notant comment le modèle change et en pensant toujours à la théorie sous-jacente à votre modèle, vous pouvez déchirer les relations intéressantes dans vos données.

Étape 2 : Évaluer le modèle

Chaque fois que vous ajoutez ou soustrayez une variable, vous devez évaluer la précision du modèle en examinant son coefficient de détermination (^R2), son AICR et ses tracés résiduels. Chaque fois que vous modifiez le modèle, comparez les nouveaux tracés R², AICR et résiduels aux anciens afin de déterminer si le modèle s’est amélioré ou non.

R au carré (^R2)

La métrique numérique permettant de quantifier la précision des prévisions du modèle est connue sous le nom de coefficient de détermination (R²), qui se situe entre zéro et un. Un zéro signifie que le modèle n’a pas de valeur prédictive et qu’un seul signifie que le modèle prédit parfaitement tout.

Par exemple, le modèle à gauche est plus précis que celui de droite ; c’est-à-dire que si vous connaissez “Température”, vous avez une assez bonne idée de ce que sera “Revenu” à gauche, mais pas vraiment à droite.

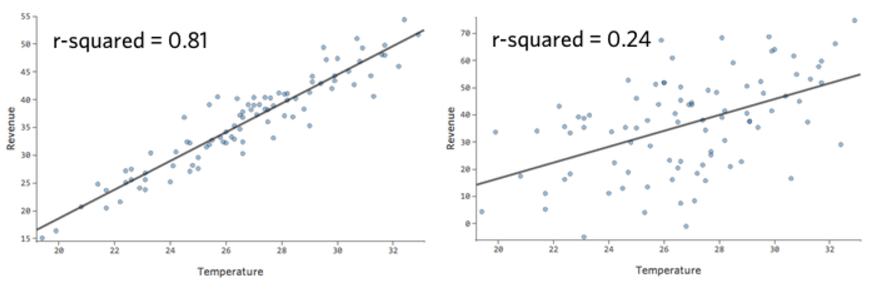
Il n’existe pas de définition fixe d’un « bon » coefficient de détermination. Dans certaines options, il peut être intéressant de voir n’importe quel effet, tandis que dans d’autres, votre modèle peut être inutile, sauf s’il est très précis.

Chaque fois que vous ajoutez une variable, le coefficient de détermination (R²) augmente. L’objectif n’est donc pas d’atteindre le coefficient de détermination le plus élevé possible. Vous voulez plutôt équilibrer la précision du modèle (R²) avec sa complexité (en général, le nombre de variables qu’il contient).

AICR

AICR est une métrique qui équilibre la précision avec la complexité – une précision accrue conduit à de meilleurs scores, une complexité supplémentaire (plus de variables) conduit à des scores moins bons. Le modèle avec l’AICR inférieur est meilleur.

Notez que la métrique AICR n’est utile que pour comparer les AICR de modèles ayant le même nombre de lignes de données etla même variable de sortie.

Intervalles de prédiction

Une autre façon utile d’avoir une idée de la précision de votre modèle est de coller les valeurs d’échantillon dans votre formule et de voir l’intervalle de prédiction que Stats iQ calcule. Par exemple, si vous collez le nombre 30 dans la formule, Stats iQ vous dira que la valeur prédite est 45,5, mais que l’intervalle de confiance à 95 % est compris entre 36,4 et 54,5, ce qui signifie que vous pourriez être sûr à 95 % que si demain il s’avérait être 30 degrés, vous obtiendriez entre 36,40 $ et 54,50 $ dans « Chiffre d’affaires ». Vous pourriez imaginer un modèle plus précis où l’intervalle de prédiction était une bande serrée comme 44$ à 48$, ou une moins précise où l’intervalle était large, comme 20 à 72$.

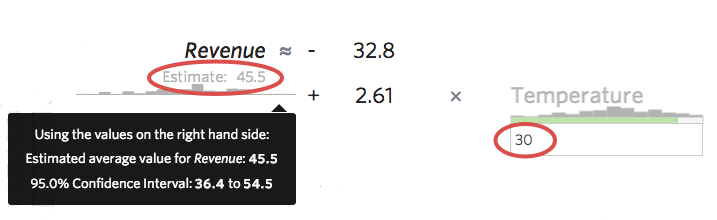
Cette approche n’est utile que lorsque vos parcelles résiduelles semblent saines (voir ci-dessous), sinon elles seront inexactes.

Résidus

Les résidus sont le principal outil de diagnostic pour évaluer et améliorer la régression. Il existe donc une section distincte sur l’interprétation des résidus pour améliorer votre modèle. Vous allez apprendre ou rafraîchir votre mémoire sur les résidus, comment les utiliser pour évaluer et améliorer le modèle, et comment réfléchir à la précision dont vous avez besoin pour votre modèle.

Nous vous recommandons de le lire intégralement, car il couvrira tout le reste dont vous avez besoin pour produire un modèle super. Mais vous pouvez toujours y revenir, bien sûr.

Étape 3 : Modifiez le modèle en conséquence

Si votre évaluation du modèle a révélé qu’il était satisfaisant, soit vous avez terminé, soit vous pouvez revenir à la phase 1 et saisir plus de variables.

Si votre évaluation trouve le modèle manquant, vous utiliserez les alertes de Stats iQ et la section de diagnostic résiduel pour résoudre les problèmes.

Lorsque vous modifiez le modèle, notez continuellement les changements de R², AICR et diagnostics résiduels, et décidez si les modifications que vous apportez aident ou nuisent à votre modèle.

FAQ