La Matrice de Confusion et le compromis précision-rappel
La matrice de confusion et le tableau de rappel de précision vous aident à évaluer la précision de votre modèle.
Matrice de confusion
Imaginons que vous envisagiez d’offrir un morceau de sucre supplémentaire aux clients susceptibles de revenir. Bien entendu, pour éviter de distribuer inutilement des morceaux de sucre, vous ne les donnez qu’aux clients dont le modèle indique qu’ils ont au moins 30 % de chances de revenir.
Si de nouveaux clients passaient devant vous..
| Identifiant du client | Âge | Sexe |
|---|---|---|
| … | … | … |
| 324 | 54 | Femme |
| 325 | 23 | Femme |
| 326 | 62 | Homme |
| 327 | 15 | Femme |
| … | … | … |
  ;
…vous pourriez utiliser notre modèle de régression pour prédire la probabilité qu’ils reviennent..
| Identifiant du client | Âge | Sexe | Probabilité de retour estimée par le modèle |
|---|---|---|---|
| … | … | … | … |
| 324 | 54 | Femme | 34% |
| 325 | 23 | Femme | 24% |
| 326 | 62 | Homme | 65% |
| 327 | 15 | Femme | 7% |
| … | … | … | … |
  ;
…et décide de classer les clients ayant une probabilité d’au moins 30 % comme “reviendront” et de leur donner des morceaux de sucre :
| Identifiant du client | Âge | Sexe | Probabilité de retour estimée par le modèle | Prédiction du modèle (seuil de 30%) |
|---|---|---|---|---|
| … | … | … | … | … |
| 324 | 54 | Femme | 34% | Reviendra |
| 325 | 23 | Femme | 24% | Ne le fera pas |
| 326 | 62 | Homme | 65% | Reviendra |
| 327 | 15 | Femme | 7% | Ne le fera pas |
| … | … | … | … | … |
  ;
Pour mieux comprendre la précision de notre modèle, vous pouvez l’appliquer aux points de données dont vous disposez déjà, où vous savez déjà si ce client est finalement revenu..
| Identifiant du client | Âge | Sexe | Probabilité de retour estimée par le modèle | Prédiction du modèle (seuil de 30%) |
Renvoyé |
|---|---|---|---|---|---|
| 1 | 21 | Homme | 44% | Reviendra | Renvoyé |
| 2 | 34 | Femme | 4% | Ne le fera pas | Renvoyé |
| 3 | 13 | Femme | 65% | Reviendra | Ne l’a pas fait |
| 4 | 25 | Femme | 27% | Ne le fera pas | Ne l’a pas fait |
| … | … | … | … | … | … |
  ;
…et évaluer le degré de précision des données..
| CustomerID | Âge | Sexe | Probabilité de retour estimée par le modèle | Prédiction du modèle (seuil de 30%) |
Renvoyé | Précision de la prédiction |
|---|---|---|---|---|---|---|
| 1 | 21 | Homme | 44% | Reviendra | Renvoyé | Correct |
| 2 | 34 | Femme | 4% | Ne le fera pas | Renvoyé | Incorrect |
| 3 | 13 | Femme | 65% | Reviendra | Ne l’a pas fait | Incorrect |
| 4 | 25 | Femme | 27% | Ne le fera pas | Ne l’a pas fait | Correct |
| … | … | … | … | … | … | … |
  ;
…et les répartir ensuite dans les catégories suivantes :
- Vrai positif: Classé par le modèle comme “reviendra” et qui est en fait “revenu” dans la réalité.
- Faux positif: Classé par le modèle comme “reviendra” mais en réalité “n’est pas revenu”.
- Vrai négatif: Classé par le modèle comme “ne reviendra pas” et en fait “n’est pas revenu” dans la réalité.
- Faux négatif: Classé par le modèle comme “ne reviendra pas” mais qui est en réalité “revenu”.
| Identifiant du client | Âge | Sexe | Probabilité de retour estimée par le modèle | Prédiction du modèle (seuil de 30%) |
Renvoyé | Précision de la prédiction | Type de précision |
|---|---|---|---|---|---|---|---|
| 1 | 21 | Homme | .44 | Reviendra | Renvoyé | Correct | Vrai positif |
| 2 | 34 | Femme | .04 | Ne le fera pas | Renvoyé | Incorrect | Faux négatif |
| 3 | 13 | Femme | .65 | Reviendra | Ne l’a pas fait | Incorrect | Faux positif |
| 4 | 25 | Femme | .27 | Ne le fera pas | Ne l’a pas fait | Correct | Vrai négatif |
| … | … | … | … | … | … | … | … |
  ;
Enfin, on pourrait résumer tout ce travail en termes de précision et de rappel.
Précision:
- Parmi les personnes classées dans la catégorie “reviendra”, quelle est la proportion de celles qui sont effectivement revenues ?
- Vrai positif / (Vrai positif + Faux positif)
Rappel:
- Rappel : Parmi ceux qui sont effectivement “retournés”, quelle est la proportion de ceux qui ont été classés dans cette catégorie ?
- Vrai positif / (Vrai positif + Faux négatif)
Les meilleurs modèles ont des valeurs plus élevées pour la précision et le rappel.
- Vous pouvez imaginer un modèle avec une précision de 94 % (presque toutes les personnes identifiées comme “reviendront” reviennent effectivement) et un rappel de 97 % (presque toutes les personnes qui “reviennent” sont identifiées comme telles).
- Un modèle plus faible peut avoir une précision de 95 % mais un rappel de 50 % (lorsqu’il identifie quelqu’un comme “reviendra”, il est en grande partie correct, mais il qualifie à tort de “ne reviendra pas” la moitié des personnes qui sont en fait revenues plus tard).
- Ou bien le modèle a une précision de 60 % et un rappel de 60 %.
Ces chiffres devraient vous donner une bonne idée de la précision de votre modèle, même si vous ne souhaitez jamais faire de prédictions.
Précision vs. Courbe de rappel
Au sein d’un même modèle, vous pouvez également décider de mettre l’accent sur la précision ou le rappel. Peut-être êtes-vous à court de morceaux de sucre et ne voulez-vous les distribuer qu’aux personnes dont vous êtes sûr qu’elles reviendront, alors vous décidez de ne les donner qu’aux clients qui ont 60 % de chances de revenir (au lieu de 30 %).
Notre précision augmentera parce que vous ne distribuerez des morceaux de sucre que lorsque vous aurez la certitude que quelqu’un “reviendra” Notre nombre de rappels diminuera parce qu’il y aura beaucoup de personnes qui finiront par “revenir” et à qui vous n’étiez pas assez confiant pour donner un morceau de sucre.
Précision : 62% -> ; 80%Rappel
:
60% -> ; 30%Ou
, si vous vous sentez riche en morceaux de sucre, vous pouvez les distribuer à tous ceux qui ont au moins 10% de chances de revenir.
Précision : 62% -> ; 40%Rappel
:
60 % -> ; 90 %Ce
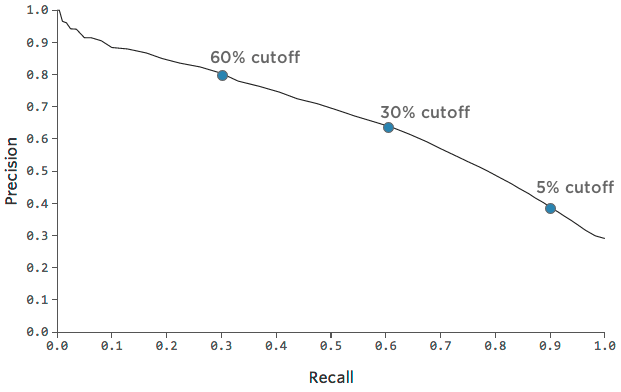
graphique permet de visualiser le compromis entre la précision et le rappel :
Il peut être utile de choisir un point sur le graphique qui représente un bon mélange de précision et de rappel, puis de se faire une idée de la précision du modèle à ce point.