Scripts R pré-composés
À propos des scripts R précomposés
R est un langage de programmation statistique largement utilisé pour des analyses flexibles et puissantes. Lorsque vous utilisez R Coding dans Stats iQ, vous pouvez sélectionner plusieurs scripts d’analyse pour rendre l’utilisation de R plus facile et plus efficace.
Sélection d’un script pour le code R
- Sélectionnez les variables que vous souhaitez analyser. Pour plus d’informations, voir Sélection des variables de la base de données pour le code R.
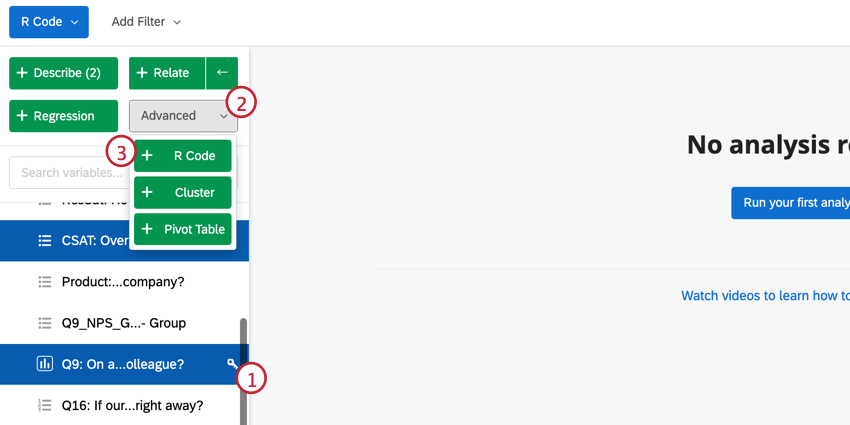
- Cliquez sur Avancé.
- Cliquez sur le code R.
- Sélectionnez un script. Pour plus d’informations sur les options d’analyse, voir les sections ci-dessous.
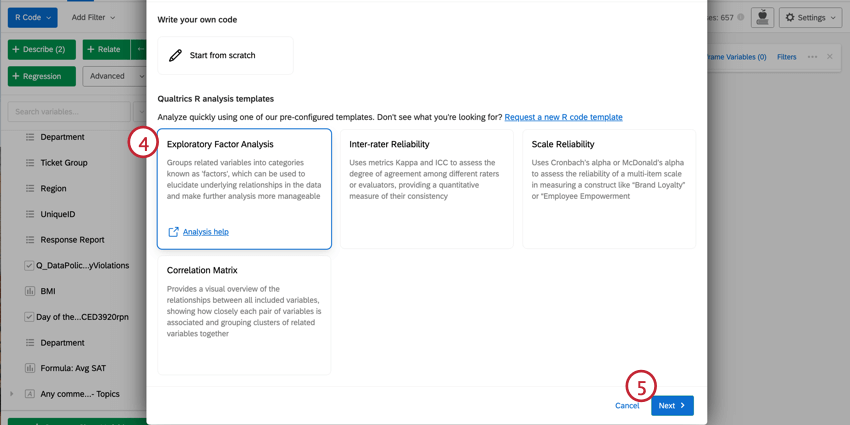
- Cliquez sur Suivant.
- Confirmez les variables que vous avez sélectionnées. Si vous souhaitez modifier une variable, cliquez sur la liste déroulante et sélectionnez-en une nouvelle.
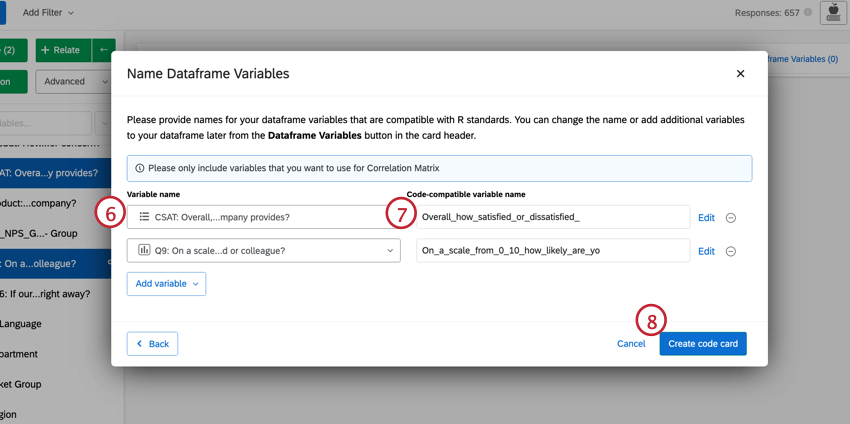
- Modifiez le nom de vos variables, si vous le souhaitez. Pour plus d’informations, voir Nommer les variables de la base de données pour le code R.
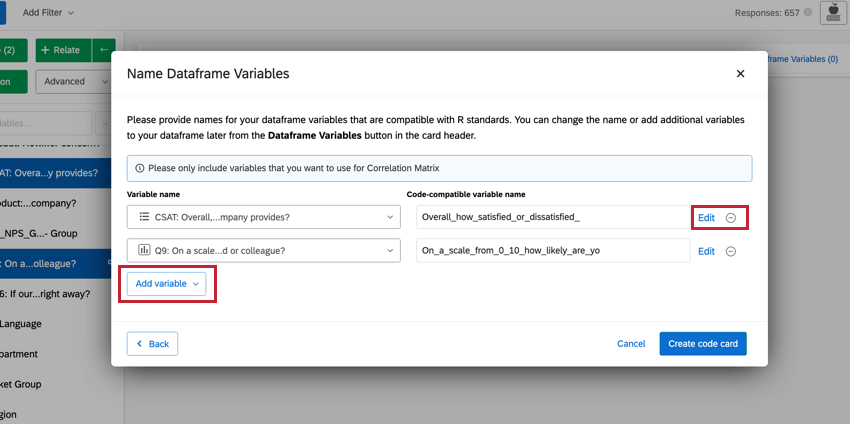
Astuce: Vous pouvez apporter des modifications aux variables que vous avez sélectionnées directement à partir de cette fenêtre. Pour modifier les Valeurs recodées, cliquez sur Modifier. Si vous souhaitez supprimer la variable, cliquez sur l’icône ( – ). Si vous souhaitez ajouter une nouvelle variable, cliquez sur Ajouter une variable en bas à gauche.
- Lorsque vous avez fini de modifier les variables de votre dataframe, cliquez sur Créer une carte de code.
Naviguer dans les scripts de code R pré-composés
Votre script sera collé dans la section code de la carte R Code. Ce code contiendra des conseils ainsi que les commandes permettant de générer l’analyse que vous avez sélectionnée. Pour exécuter votre analyse, cliquez sur Exécuter tout. Les résultats s’affichent dans la boîte de sortie à droite.
Vous pouvez modifier les variables de votre cadre de données ou ajouter un filtre à l’analyse en cliquant sur les options en haut à droite. Cliquez sur le menu à trois points pour ajouter des notes à votre carte de code, copier l’analyse ou ouvrir la carte en plein écran.
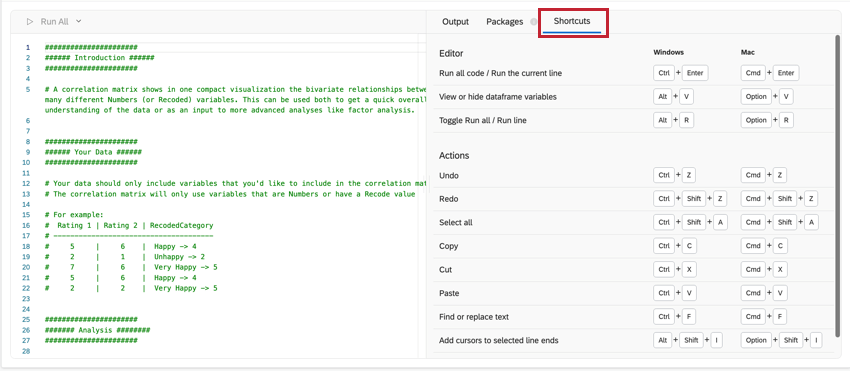
SHORTCUTS
Des raccourcis clavier peuvent être utilisés pour naviguer plus efficacement dans la carte R Code. Cliquez sur Raccourcis pour obtenir la liste des actions possibles.
PACKAGES
Le codage R dans Stats iQ est préinstallé avec des centaines de paquets R parmi les plus populaires utilisés pour l’analyse. Cliquez sur l’onglet Forfaits dans la moitié droite de la carte pour voir la liste des forfaits disponibles. Pour plus d’informations sur l’utilisation des packages, voir R Coding in Stats iQ.
Fiabilité des échelles
La fiabilité de l’échelle évalue la mesure dans laquelle les éléments d’une échelle à plusieurs éléments peuvent mesurer un concept de manière fiable. En d’autres termes, si la même chose est mesurée à l’aide de la même série de questions, les résultats seront-ils fiables et similaires ? Si c’est le cas, il est certain que tout changement observé à l’avenir est dû à des modifications de la population enquêtée ou à des interventions qui ont été faites pour améliorer le score.
L’INTERPRÉTATION DES MESURES DE FIABILITÉ
Les mesures de fiabilité d’une échelle se situent entre 0 et 1 et représentent essentiellement une corrélation globale entre tous les éléments de l’échelle.
L’alpha de Cronbach, une mesure de fiabilité largement utilisée, sous-estime souvent la fiabilité en raison de certaines hypothèses. L’oméga de McDonald’s, une alternative recommandée, évite ces défauts. Nous utilisons par défaut l’oméga de McDonald, mais l’alpha de Cronbach est encore largement accepté.
Il n’y a pas une seule façon correcte d’interpréter le nombre résultant, mais notre règle empirique préférée pour les deux omégas est décrite ci-dessous :
| Moins de 0,65 | Inacceptable |
| 0.65 | Acceptables |
| 0.8 | Très bien |
Si votre échelle fiable est inacceptable, il existe quelques options pour remédier à votre jeu de données :
- Retirez tous les éléments qui font baisser l’oméga ou l’alpha.
- Il est possible que deux concepts distincts soient mesurés. Si c’est le cas, la séparation des variables en deux groupes et la réalisation de l’analyse sur chacun d’entre eux conduiraient à des scores de fiabilité plus élevés que ceux de l’analyse initiale. Vous pouvez étudier cette question en évaluant la matrice de corrélation dans les résultats ou en utilisant le script d’analyse factorielle exploratoire pour voir quels sont les regroupements qui se dégagent naturellement des données.
- En fin de compte, il peut s’avérer nécessaire de modifier et d’exécuter à nouveau l’enquête. Les éléments qui ont une faible corrélation avec les autres peuvent devoir être clarifiés ou retravaillés, ou d’autres éléments peuvent devoir être ajoutés.
Des résultats très élevés (par exemple, 0,95) peuvent également indiquer un problème avec l’échelle, généralement parce qu’il est possible d’avoir une échelle très fiable sans avoir autant d’items. Dans ce cas, nous recommandons de supprimer les éléments les moins utiles de l’échelle et de relancer l’analyse.
L’INTERPRÉTATION DES STATISTIQUES AU NIVEAU DES ITEMS
Le script effectue d’abord une mesure de fiabilité globale, puis une itération pour chaque variable. L’objectif de l’analyse de la fiabilité par item est de comprendre quels sont les items les plus utiles à la construction de l’échelle. Stats iQ produira un tableau semblable à celui-ci :
Oméga global de McDonald’s : 0,71
| N | Moyenne | Corrélation entre l’item et le total | McDonald’s Omega si supprimé | |
| A1 | 2784 | 4.59 | 0.31 | 0.72 |
| A2 | 2773 | 4.80 | 0.56 | 0.69 |
| A3 | 2774 | 4.60 | 0.59 | 0.61 |
| … | … | … | … | … |
- L’objectif général est d’obtenir un Oméga de McDonald’s plus élevé avec un nombre d’articles plus faible. Par conséquent, si un chercheur devait créer une nouvelle échelle, il souhaiterait probablement supprimer le A1, puisque l’oméga est en fait plus élevé sans lui.
- Il appartient au chercheur de déterminer les autres éléments qui, s’ils étaient supprimés, réduiraient la fiabilité. Par exemple, si un chercheur est préoccupé par la lassitude des enquêteurs, il peut admettre une diminution plus importante de la fiabilité lorsqu’il décide de supprimer une variable.
- La corrélation item-total est la corrélation entre cet item et la moyenne de tous les autres. Une corrélation Item-Total faible suggère que la variable n’est pas suffisamment représentative du concept sous-jacent. La règle empirique la plus courante consiste à se méfier de tout ce qui présente une corrélation Item-Total de 0,3 ou moins, en particulier si vous avez beaucoup d’items, ce qui gonfle artificiellement la métrique de fiabilité.
Si vous décidez de supprimer un élément, vous devez réexécuter toutes les autres statistiques avant de décider de supprimer un autre élément. Dans Stats iQ, cela signifie qu’il suffit de supprimer la variable de l’ensemble de la carte – le reste se fera automatiquement.
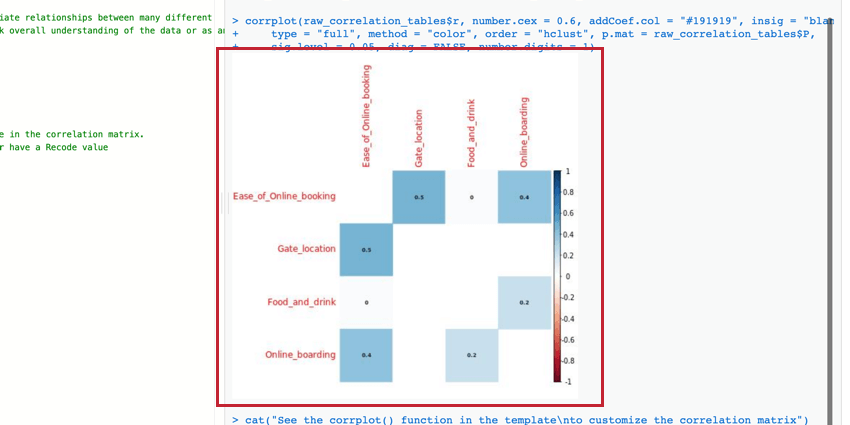
MATRICE DE CORRÉLATION INTER-ITEMS
La Matrice de corrélation inter-items montre la corrélation entre chaque variable de l’analyse et chaque autre variable. Par exemple, si une variable est très fortement corrélée à une autre (par exemple, 0,9), ces questions peuvent être redondantes et leur suppression n’aura qu’un faible impact sur votre fiabilité.
La corrélation inter-items moyenne est la moyenne des chiffres de la matrice. Des chiffres plus élevés suggèrent que certains éléments sont redondants et pourraient être supprimés. En règle générale, les variables doivent se situer entre 0,2 et 0,4.
PLUS DE RESSOURCES
- L’analyse de fiabilité dans Stats iQ est exécutée par la fonction compRelSem() du package R semTools. Divers paramètres avancés sont décrits dans la documentation. Il n’est pas nécessaire d’utiliser ou de comprendre ces informations pour effectuer une analyse de fiabilité.
- La matrice de corrélation est exécutée par la fonction corrplot() du package R corrplot. De nombreux paramètres avancés et personnalisations sont décrits dans la documentation et dans ce guide.
Fiabilité inter-juges
La fiabilité inter-évaluateurs (IRR) est utilisée pour évaluer dans quelle mesure deux évaluateurs ou plus sont d’accord dans leur évaluation. Par exemple, trois codeurs différents peuvent évaluer un commentaire de texte comme ayant un sentiment positif, neutre ou négatif ; le TRI décrit dans quelle mesure ils sont d’accord les uns avec les autres.
MESURES DE LA FIABILITÉ INTER-ÉVALUATEURS
Le TRI est évalué à l’aide de paramètres légèrement différents en fonction de la structure des données. Par exemple, une analyse de l’inter-fiabilité de deux évaluateurs utilisera une mesure légèrement différente de celle de l’inter-fiabilité de trois évaluateurs.
Stats iQ sélectionnera automatiquement la mesure appropriée pour vos données.
L’INTERPRÉTATION DES RÉSULTATS
La technologie de Kappa ou ICC est le principal résultat, compris entre 0 et 1, et indique le degré de corrélation entre les évaluateurs. Nous proposons les fourchettes suivantes pour l’interprétation du Kappa :
| 0.75 à 1 | Excellente |
| 0.6 à 0,75 | Bonne |
| 0.4 à 0,6 | Plutôt bien |
| 0.4 ou moins | Mauvaise |
PLUS DE RESSOURCES
- Cette analyse de fiabilité est réalisée à l’aide des fonctions du progiciel IRR R. Divers paramètres avancés sont décrits dans la documentation. Il n’est pas nécessaire d’utiliser ou de comprendre ces informations pour effectuer cette analyse.
Analyse des facteurs exploratoires
L’analyse factorielle exploratoire (AFE) est une technique statistique qui permet de réduire un grand nombre de variables en un ensemble plus petit et plus maniable de “facteurs” sommaires. Ils sont ainsi beaucoup plus faciles à interpréter, à communiquer et à analyser (par exemple, analyse de régression). L’AAE suit généralement cette série d’étapes :
- Diagnostics: Exécutez et interprétez une série de diagnostics qui déterminent si les données se prêtent à une analyse factorielle. Les variables doivent être suffisamment corrélées entre elles pour former des groupes significatifs, mais pas au point d’être redondantes.
- Choix des facteurs: Déterminer le nombre de facteurs présents dans les données. Les facteurs sont des regroupements de variables similaires. Par défaut, le script R utilisera un critère calculé et exécuté automatiquement.
- Nommer les facteurs: À l’issue de l’AFE, il vous restera plusieurs facteurs qui représentent le mieux les thèmes clés des données. Il est utile d’attribuer à ces facteurs des noms lisibles par l’homme qui en saisissent la signification.
- Mesures associées & ; métriques: L’analyse factorielle est effectuée avec le nombre de facteurs de l’étape précédente. Le résultat est un ensemble de groupements de variables accompagné d’une description statistique de la factorisation.
Le résultat est un ensemble de facteurs nommés et les éléments de l’enquête qui les composent. Ces facteurs peuvent servir de cadre conceptuel pour des analyses ultérieures ou être appliqués en retour aux données.
DIAGNOSTIC
Le script exécute d’abord une série de diagnostics pour s’assurer que les données sont adaptées à l’AFE :
- Taille de l’échantillon: En règle générale, un rapport de 10:1 entre les réponses et les éléments est suggéré. Par exemple, si vous avez 10 questions, vous devez avoir au moins 100 répondants.
- Test de sphéricité de Bartlett: Ce test évalue si les éléments sont suffisamment corrélés pour être utilement regroupés en facteurs. En cas d’échec, il est probable que plusieurs éléments ne soient pas suffisamment corrélés avec les autres. Vous pouvez envisager d’éliminer de votre analyse les éléments qui ne sont pas en corrélation avec d’autres, ou d’ajouter à l’enquête d’autres éléments connexes.
- Déterminant: Le déterminant évalue si les éléments sont trop fortement corrélés pour être utilement regroupés en facteurs. Si ce diagnostic échoue, il est probable que les éléments soient trop similaires pour être séparés en facteurs. Envisager de modifier les éléments de l’enquête pour les rendre plus distincts.
- Mesure de Kaiser-Meyer-Olkin (KMO) : cette mesure permet de vérifier si les éléments de votre enquête ont suffisamment de points communs pour les regrouper en facteurs significatifs. La réussite de ce diagnostic signifie que les réponses de votre enquête ont beaucoup de points communs et peuvent être regroupées de manière satisfaisante. Dans le cas contraire, les éléments ne sont pas regroupés en catégories. Si ce diagnostic échoue, vous pouvez réviser les éléments de votre enquête afin de capturer davantage de thèmes similaires et envisager de supprimer les éléments qui ne présentent pas de lien clair avec d’autres.
LE CHOIX DES FACTEURS
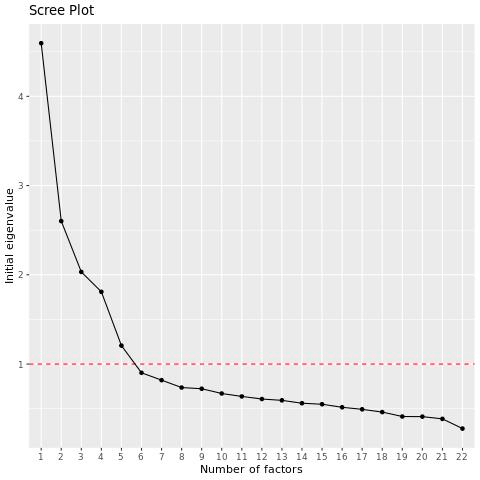
L’objectif de l’AFE est de réduire un grand nombre de variables en un nombre relativement faible de variables utiles pour l’analyse. Il se peut donc que vous deviez effectuer l’analyse factorielle plusieurs fois avec différents nombres de facteurs afin de trouver un regroupement qui vous convienne. Le script de l’EFA suggère le nombre de facteurs en utilisant leurs valeurs propres.
Le script de l’AFE produira un diagramme de tri, qui montre les valeurs propres des variables dans l’ordre décroissant. Vous pouvez examiner le graphique pour voir combien de facteurs apparaissent avant le “coude” dans le graphique, après quoi il est moins utile d’ajouter d’autres facteurs.
NOMMER SES FACTEURS
Après avoir effectué l’AFE, chaque variable est affectée à un facteur. Il est utile de donner à chaque facteur un nom qui vous permettra d’en parler de manière abrégée, ce qui rendra vos résultats plus accessibles. L’objectif est ici de simplifier vos données complexes en quelques thèmes compréhensibles.
Voici quelques conseils pour nommer vos facteurs :
- Soyez descriptif: Essayez de saisir le thème commun qui résume les variables du groupe.
- Technologie de l’information: Les noms de vos facteurs doivent être faciles à comprendre et à communiquer. Évitez le jargon technique ou les phrases trop complexes.
- Tenez compte de votre public: Les noms des facteurs doivent avoir un sens pour les personnes qui utiliseront votre analyse. Par exemple, “Propreté” serait significatif à la fois pour les managers et les clients d’un hôtel.
- Cohérence: Si votre enquête ou votre ensemble de données couvre différents domaines ou objets, veillez à ce que les noms de vos facteurs soient cohérents.
MESURES ET MÉTRIQUES ASSOCIÉES
Le tableau des charges factorielles est l’un des principaux résultats de l’EFA. La charge factorielle d’une paire variable-facteur donnée est la corrélation entre cette variable et ce facteur. Technologie de l’information : si une variable a une charge factorielle élevée pour un certain facteur, cela signifie que la question est fortement liée à ce facteur.
L’unicité est la part de la variance qui est propre à la variable spécifique et qui n’est pas partagée avec d’autres variables. Les valeurs d’unicité sont comprises entre 0 et 1, les valeurs les plus élevées indiquant que la variable est unique et ne correspond à aucun des facteurs. .
En général, il est recommandé de supprimer les variables dont la charge factorielle est supérieure à 0,3 ou dont l’unicité est supérieure à 0,7.
L’UTILISATION DE VOS RÉSULTATS
L’analyse factorielle étant un processus itératif, il se peut que vous deviez l’exécuter plusieurs fois avec différents nombres de facteurs pour trouver un regroupement qui vous convienne. Pour la plupart des chercheurs, l’essentiel est de trouver des regroupements de facteurs susceptibles d’apporter un nouvel éclairage sur leurs données, mais vous pouvez utiliser ces facteurs comme de nouvelles variables dans des analyses ultérieures – comme la régression ou l’analyse de cluster. Par exemple, vous pourriez créer une nouvelle variable pour chaque facteur qui prendrait la valeur moyenne de toutes les variables qui y sont regroupées.
Matrice de corrélation
La matrice de corrélation est un tableau qui montre la corrélation entre chaque paire de variables fournies. Ce tableau utilise par défaut le r de Pearson pour mesurer la corrélation, mais vous pouvez le remplacer par le rho de Spearman si vous le souhaitez.
Vous pouvez modifier les paramètres de la fonction corrplot() pour modifier le tableau et le rendre plus lisible. Pour plus d’informations, vous pouvez consulter la documentation officielle de R.