Analyse de la correspondance (BX)

À propos de l’analyse de la correspondance

L’analyse de correspondance révèle les relations relatives entre et au sein de deux groupes de variables, en fonction des données données dans un tableau de contingence. Pour les perceptions de la marque, ces deux groupes sont les suivants :

1. Organisations
2. Attributs qui s’appliquent à ces marques

Par exemple, supposons qu’une entreprise veuille savoir quels attributs les consommateurs associent à différentes marques de produits de boissons. L’analyse de correspondance permet de mesurer les similitudes entre les marques et la force des marques en termes de relations avec différents attributs. La compréhension des relations relatives permet aux titulaires de marques d’identifier les effets des actions précédentes sur les différents attributs liés à la marque et de décider des étapes à suivre.

L’analyse de la correspondance est précieuse dans les perceptions de la marque pour plusieurs raisons. Lorsque vous tentez d’examiner les relations relatives entre les marques et les attributs, la taille de la marque peut avoir un effet trompeur ; l’analyse de correspondance supprime cet effet. L’analyse de correspondance offre également une vue rapide intuitive des relations d’attributs de marque (basée sur la proximité et la distance par rapport à l’origine) qui n’est pas fournie par de nombreux autres graphiques.

Sur cette page, nous allons voir un exemple d’application de l’analyse de correspondance à un cas d’utilisation pour différentes marques (fictives) de produits à base de soude.

Commençons par le format des données d’entrée : un tableau de contingence.

Tables des éventualités

Un tableau de contingence est un tableau à deux dimensions comportant des groupes de variables sur les lignes et les colonnes. Si nos groupes, comme décrit ci-dessus, étaient des marques et leurs attributs associés, nous exécuterions des enquêtes et obtiendrions différents nombres de réponses associant différentes marques aux attributs donnés. Chaque cellule du tableau représente le nombre de réponses ou de nombres associant cet attribut à cette marque. Cette « association » s’afficherait par le biais d’une question de l’enquête telle que « Choisir des marques dans une liste en dessous de laquelle vous pensez afficher l’attribut ___ ».

Ici, les deux groupes sont “Marques” (lignes) et “Attributs” (colonnes). La cellule dans le coin inférieur droit représente le nombre de réponses pour la marque “Brawndo” et l’attribut “Economique”.

Résidus (R)

Dans l’analyse de correspondance, nous voulons examiner les résidus de chaque cellule. Un résiduel quantifie la différence entre les données observées et les données que nous attendons, en supposant qu’il n’existe aucune relation entre les catégories de ligne et de colonne (ici, il s’agit de la marque et de l’attribut). Un résiduel positif nous montre que le nombre pour cet appariement d’attributs de marque est beaucoup plus élevé que prévu, ce qui suggère une relation forte ; en conséquence, un résiduel négatif affiche une valeur inférieure à celle attendue, ce qui suggère une relation plus faible. Avançons le calcul de ces résidus.

Un (R) résiduel est égal à : R = P – E, où P est les proportions observées et E les proportions attendues pour chaque cellule.  Décomposons ces proportions observées et attendues !

Proportions observées (P)

Une proportion observée (P) est égale à la valeur d’une cellule divisée par la somme totale de toutes les valeurs du tableau. Ainsi, pour notre tableau des aléas ci-dessus, la somme totale serait : 5 + 7 + 2 + 18 … + 16 = 312. En divisant chaque valeur de cellule par le total des résultats dans le tableau ci-dessous pour les proportions observées (P).

Par exemple, dans la cellule en bas à droite, nous avons pris notre valeur de cellule initiale 16/312 = 0,051. Cela nous indique la proportion de l’ensemble de notre graphique que l’appariement de Brawndo et Economic représente sur la base de nos données collectées.

Masses de lignes et de colonnes

Quelque chose que nous pouvons calculer facilement à partir de nos proportions observées, et sera utilisé beaucoup plus tard, ce sont les sommes des lignes et des colonnes de notre table de proportions, connues sous le nom de masses de lignes et de colonnes. Une masse de ligne ou de colonne est la proportion de valeurs pour cette ligne/colonne. La masse de rangée pour “Butterbeer,” regardant notre classement ci-dessus, serait 0,016 + 0,022 + 0,006, ce qui nous donne 0,044.

Pour effectuer des calculs similaires, nous obtenons les résultats suivants :

Proportions attendues (E)

Les proportions attendues (E) seraient ce que nous nous attendons à voir dans la proportion de chaque cellule, en supposant qu’il n’existe aucune relation entre les lignes et les colonnes. Notre valeur attendue pour une cellule serait la masse de ligne de cette cellule multipliée par la masse de la colonne de cette cellule.

Voir dans la cellule en haut à gauche, la masse de rangée pour Butterbeer multipliée par la masse de colonne pour Tasty, 0,044 * 0,182 = 0,008.

Nous pouvons maintenant calculer notre table des résidus (R), où R = P – E. Les résidus quantifient la différence entre nos proportions de données observées et nos proportions de données attendues, si nous supposons qu’il n’existe aucune relation entre les lignes et les colonnes.

Prenant notre valeur la plus négative de -0,045 pour Squishee et Economic, ce que nous interpréterions ici, c’est qu’il existe une association négative entre Squishee et Economic ; Squishee est beaucoup moins susceptible d’être considéré comme “économique” que nos autres marques de boissons.

Résidus indexés (I)

Il existe cependant des problèmes de lecture des résidus.

En regardant la ligne supérieure de notre table de calcul des résidus ci-dessus, nous constatons que tous ces nombres sont très proches de zéro. Nous ne devrions pas en tirer la conclusion évidente que Butterbeer n’est pas lié à nos attributs, car cette hypothèse est incorrecte. L’explication réelle serait que les proportions observées (P) et les proportions attendues (E) sont faibles car, comme nous le dit notre masse de rangée, seulement 4,4% de l’échantillon sont Butterbeer.

Cela pose un gros problème en ce qui concerne l’examen des résidus, dans la mesure où nous ignorons le nombre réel d’enregistrements dans les lignes et les colonnes, nos résultats sont décalés vers les lignes/colonnes avec des masses plus importantes. Nous pouvons y remédier en divisant nos résidus par nos proportions attendues (E), nous donnant un tableau de nos résidus indexés (I, I = R / E) :

Les résidus indexés sont faciles à interpréter : plus la valeur du tableau est importante, plus la proportion observée par rapport à la proportion attendue est importante.

Par exemple, en prenant la valeur en haut à gauche, Butterbeer est 95 % plus susceptible d’être considéré comme “Tasty” que ce que nous attendions s’il n’y avait pas de relation entre ces marques et attributs. Alors qu’en haut à droite, Butterbeer est 65 % moins susceptible d’être considéré comme « économique » que ce que nous attendions, étant donné qu’il n’y a pas de relation entre nos marques et nos attributs.

Compte tenu de nos résidus indexés (I), de nos proportions attendues (E), de nos proportions observées (P) et de nos masses de lignes et de colonnes, commençons à calculer nos valeurs d’analyse de correspondance pour notre graphique !

Calcul des coordonnées pour l’analyse de la correspondance

Décomposition de la valeur individuelle (SVD)

Notre première étape consiste à calculer la décomposition de la valeur singulière, ou SVD. Le SVD nous donne des valeurs pour calculer la variance et tracer nos lignes et colonnes (marques et attributs).

On calcule le SVD sur le résiduel normalisé (Z), où Z = I * sqrt(E), où I est notre résiduel indexé, et E est nos proportions attendues. La multiplication par E entraîne la pondération de notre SVD, de sorte que les cellules ayant une valeur attendue plus élevée reçoivent un poids plus élevé, et inversement, ce qui signifie que comme les valeurs attendues sont souvent liées à la taille de l’échantillon, les cellules “plus petites” de la table, où l’erreur d’échantillonnage aurait été plus grande, sont sous-pondérées. Ainsi, l’analyse de correspondance à l’aide d’un tableau de contingence est relativement robuste par rapport aux valeurs aberrantes causées par l’erreur d’échantillonnage.

De retour à notre SVD, nous avons : SVD = svd(Z). Une décomposition de valeur singulière génère 3 sorties :

Un vecteur, d, contenant les valeurs singulières.

Une matrice, u, contenant les vecteurs singuliers de gauche (marques).

Une matrice, v, contenant les vecteurs singuliers droits (attributs).

Les vecteurs singuliers de gauche correspondent aux catégories dans les rangées du tableau, et les vecteurs singuliers de droite correspondent aux colonnes. Chacune des valeurs singulières, pour calculer la variance, et les vecteurs correspondants (c’est-à-dire les colonnes de u et v), pour les positions de traçage, correspondent à une dimension. Les coordonnées utilisées pour tracer les catégories de lignes et de colonnes pour notre diagramme d’analyse de correspondance sont dérivées des deux premières dimensions.

Variance exprimée par nos dimensions

Les valeurs singulières au carré sont appelées valeurs propres (d^2). Dans notre exemple, les valeurs propres sont 0.0704, 0.0129 et 0.0000. Exprimer chaque valeur propre comme proportion de la somme totale nous indique le montant de variance capturé dans chaque dimension de notre analyse de correspondance, en fonction de la valeur singulière de chaque dimension ; nous obtenons 84,5 % de la variance exprimée par notre première dimension, et 15,5 % dans notre deuxième dimension (notre troisième dimension explique 0 % de la variance).

Analyse de la correspondance standard

Nous sommes maintenant équipés des ressources pour calculer la forme de base de l’analyse de correspondance, en utilisant ce que l’on appelle des coordonnées standard, calculées à partir de nos vecteurs singuliers gauche et droit. Auparavant, nous avions pondéré les résidus indexés avant d’effectuer la SVD. Pour obtenir des coordonnées qui représentent nos résidus indexés, nous devons maintenant dépondérer les sorties de SVD, en divisant chaque rangée des vecteurs singuliers de gauche par la racine carrée des masses des rangées, et en divisant chaque colonne des vecteurs singuliers de droite par la racine carrée des masses de colonne, en nous obtenant les coordonnées standard des lignes et des colonnes pour le tracement.

Coordonnées standard de la marque :

Coordonnées standard d’attribut :

Nous utilisons les deux dimensions ayant la variance la plus élevée capturée pour le traçage, la première dimension allant sur l’axe X et la deuxième dimension sur l’axe Y, générant notre graphique d’analyse de correspondance standard.

Nous avons défini la base des calculs dont nous avons besoin pour l’analyse de correspondance standard. Dans la section suivante, nous allons explorer les avantages et les inconvénients des différents styles d’analyse de correspondance, et qui correspondent le mieux à nos objectifs d’aider à l’analyse des perceptions de la marque.

Types d’analyse de correspondance

Analyse de correspondance principale ligne/colonne

L’analyse de correspondance standard est facile à calculer et de solides résultats peuvent en être tirés. Cependant, la correspondance standard est un mauvais choix pour nos besoins ; les distances entre les coordonnées de ligne et de colonne sont exagérées et il n’y a pas d’interprétation simple des relations entre les catégories de lignes et de colonnes. Ce que nous voulons pour interpréter les relations entre les coordonnées de ligne (marque) et les relations d’interprétation entre les catégories de lignes et de colonnes, c’est la normalisation principale de ligne (ou, si nos marques étaient sur nos colonnes, la normalisation principale de colonne).

Pour la normalisation principale de ligne, vous souhaitez utiliser les coordonnées standard calculées ci-dessus pour les valeurs de colonne (d’attribut), mais vous souhaitez calculer les coordonnées principales pour les valeurs de ligne (de marque). Le calcul des coordonnées principales est aussi simple que de prendre les coordonnées standard, et de les multiplier par leurs valeurs singulières correspondantes (d). Ainsi, pour nos lignes, nous voulons simplement multiplier nos coordonnées de ligne standard par nos valeurs singulières (d), indiquées dans le tableau ci-dessous. Pour la normalisation des principaux de colonnes, nous multiplions simplement nos colonnes au lieu de nos lignes par nos valeurs singulières (d).

En remplaçant dans nos coordonnées principales nos lignes (marques), nous finissons par :

Parce que nous avons mis à l’échelle par nos valeurs singulières, nos coordonnées principales pour nos lignes représentent la distance entre les profils de lignes de notre table d’origine; on peut interpréter les relations entre nos coordonnées de lignes dans notre diagramme d’analyse de correspondance par leur proximité les unes des autres.

La distance entre nos coordonnées de colonnes, puisqu’elles sont basées sur des coordonnées standard, est encore exagérée. De plus, notre mise à l’échelle selon nos valeurs singulières dans une seule des deux catégories (lignes/colonnes) nous a donné un moyen d’interpréter les relations entre les catégories de ligne et de colonne. Compte tenu d’une valeur de ligne et d’une valeur de colonne, par exemple Butterbeer (ligne) et Tasty (colonne), plus leur distance par rapport à l’origine est longue, plus leur association avec les autres points de la carte est forte. Aussi, plus l’angle entre les deux points (Butterbeer et Tasty) est petit, plus la corrélation entre les deux est élevée.

La distance jusqu’à l’origine combinée avec l’angle entre les deux points est l’équivalent de la prise du produit point ; le produit point entre une valeur de ligne et de colonne mesure la force de l’association entre les deux. En fait, lorsque la première et la deuxième dimension expliquent l’ensemble de la variance dans les données (totaliser à 100%), le produit point est directement égal au résiduel indexé des deux catégories. Ici, le produit point serait la distance à l’origine des deux points multipliés par le cosinus de l’angle qui les sépare; .59*2.12*cos(41) = .94. En tenant compte des erreurs d’arrondi, c’est la même chose que notre valeur résiduelle indexée de 0,95. Ainsi, les angles inférieurs à 90 degrés représentent un résiduel indexé positif et donc une association positive, et les angles supérieurs à 90 degrés représentent une association résiduelle ou négative indexée négative.

Analyse de correspondance principale de ligne mise à l’échelle

En regardant notre graphique ci-dessus pour la normalisation principale des lignes, nous avons une observation facile : les points de nos colonnes (traits) sont beaucoup plus dispersés, et nos points pour nos rangées (marques) sont regroupés autour de l’origine. Cela peut rendre l’analyse de notre graphique à l’œil plutôt difficile et peu intuitive, et parfois impossible de lire les catégories de lignes si elles se chevauchent toutes. Heureusement, il existe un moyen simple d’adapter notre graphique pour inclure nos colonnes, tout en conservant la possibilité d’utiliser le produit point (distance par rapport à l’origine et angle entre les points) pour analyser les relations entre nos points de ligne et de colonne, connus sous le nom de normalisation principale de ligne mise à l’échelle.

La normalisation principale de ligne mise à l’échelle prend la normalisation principale des lignes, et met à l’échelle les coordonnées de la colonne de la même manière que nous avons mis à l’échelle l’axe x des coordonnées de lignes, c’est-à-dire que nos coordonnées de colonne sont mises à l’échelle par la première valeur de nos valeurs singulières (d). Nos valeurs de ligne restent identiques à la normalisation principale des lignes, mais maintenant nos coordonnées de colonne sont réduites par un facteur constant.

Cela signifie pour nous que nos coordonnées de colonnes sont mises à l’échelle pour s’adapter beaucoup mieux à nos coordonnées de lignes, ce qui facilite grandement l’analyse des tendances. Parce que nous avons mis à l’échelle toutes nos coordonnées de colonne par le même facteur constant, nous avons contracté la dispersion de nos coordonnées de colonne sur la carte, mais nous n’avons apporté aucune modification à leurs relativités ; nous utilisons toujours le produit point pour mesurer la force des associations. Le seul changement est que lorsque nos première et deuxième dimensions couvrent l’ensemble de l’écart dans les données, au lieu que le reliquat indexé soit égal au produit point des deux catégories, il est maintenant égal au produit point échelonné des deux catégories, qui est le produit point échelonné par une valeur constante de notre première valeur singulière(d). L’interprétation du diagramme reste identique à la normalisation principale des lignes.

Analyse principale de la correspondance

Une dernière forme d’analyse de correspondance que nous mentionnerons est l’analyse de correspondance principale, aussi connue sous le nom de carte symétrique, de mise à l’échelle du français ou d’analyse canonique de correspondance. Au lieu de multiplier uniquement les lignes ou colonnes standard par les valeurs singulières(d) comme dans l’analyse de correspondance principale ligne/colonne, nous multiplions les deux par les valeurs singulières. Nos valeurs de colonne standard, multipliées par les valeurs singulières, deviennent :

En les mettant en relation avec nos valeurs de ligne calculées dans l’analyse principale de ligne, nous obtenons :

L’analyse canonique de la correspondance met à l’échelle les coordonnées des lignes et des colonnes en fonction des valeurs singulières. Cela signifie que nous pouvons interpréter nos relations entre nos coordonnées de ligne comme nous l’avons fait dans l’analyse de correspondance principale en ligne (basée sur la proximité), ET nous pouvons interpréter nos relations entre nos coordonnées de colonne de la même manière que l’analyse de correspondance principale de colonne ; nous pouvons analyser les relations entre les marques et les relations entre les attributs. Nous perdons également le regroupement ligne/colonne au centre de la carte à partir de l’analyse principale ligne/colonne. Cependant, ce que nous perdons de l’analyse canonique de la correspondance, c’est une façon d’interpréter les relations entre nos marques et nos attributs, quelque chose de très utile dans les perceptions de marque.

Comparaison côte à côte

Analyse de la correspondance standard

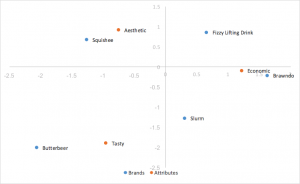
Style d’analyse de correspondance le plus facile à calculer, à l’aide des vecteurs singuliers gauche et droite de SVD divisés par les masses rangée et colonne. Les distances entre les coordonnées de ligne et de colonne sont exagérées et il n’y a pas d’interprétation simple des relations entre les catégories de ligne et de colonne.

Normalisation principale de ligne – Analyse de correspondance

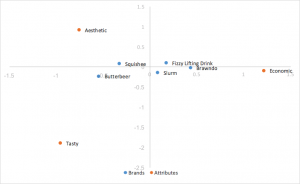
Utilise des coordonnées standard de au-dessus, mais multiplie les coordonnées de ligne par les valeurs singulières pour normaliser. Les relations entre les lignes (marques) sont basées sur la distance les unes par rapport aux autres. Les distances de colonne (attribut) sont encore exagérées. Les relations entre les lignes et les colonnes peuvent être interprétées par le produit point. Les rangées (marques) ont tendance à être claquées au centre.

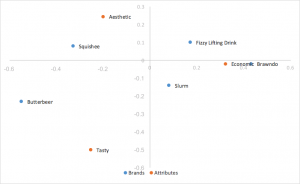
Normalisation principale de la ligne mise à l’échelle – Analyse de correspondance

Utilise la normalisation principale des lignes et met à l’échelle les coordonnées des colonnes par une constante de la première valeur singulière. Mêmes interprétations dessinées que la normalisation principale de ligne, en remplaçant le produit point par le produit point mis à l’échelle. Permet de supprimer l’agrégation des lignes au centre. C’est le style d’analyse de correspondance que nous préférons.

Normalisation principale Analyse de correspondance (symétrique, carte française, canonique)

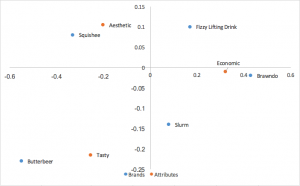
Une autre forme populaire d’analyse de correspondance utilisant les coordonnées normalisées principales dans les lignes et les colonnes. Les relations entre les lignes (marques) peuvent être interprétées par distance entre elles ; il en va de même pour les colonnes (attributs). Aucune interprétation ne peut être dessinée pour les relations entre les lignes et les colonnes.

Récapitulatif

En conclusion, l’analyse de correspondance est utilisée pour analyser les relations relatives entre et au sein de deux groupes ; dans notre cas, ces groupes seraient des marques et des attributs.

L’analyse de correspondance élimine les résultats de masses différentes entre les groupes en utilisant des résidus indexés. Pour les perceptions de la marque pour l’analyse de correspondance, nous utilisons la normalisation principale de ligne (ou principale de colonne si les marques sont placées sur les colonnes), car cela nous permet d’analyser les relations entre les différentes marques par leur proximité, et aussi d’analyser les relations entre les marques et les attributs par leur distance par rapport à l’origine combinée à l’angle entre elles et l’origine (le produit point), au sacrifice de la mauvaise représentation de la relation entre les attributs avec des distances exagérées (que nous ne prenons pas en compte). Nous utilisons la normalisation principale de ligne/colonne mise à l’échelle pour faciliter l’analyse de notre graphique sans coût. Nous voulons nous assurer de garder à l’esprit que nous additionnons l’écart expliqué à partir des étiquettes des axes X et Y (la première et la deuxième dimension) pour afficher l’écart total capturé dans la carte. Plus ce nombre est faible, plus il y a de variance inexpliquée dans les données, et plus le tracé est trompeur.

Une dernière chose à retenir est que l’analyse de la correspondance ne montre que des relativités puisque nous avons éliminé le facteur de masse de nos données; notre graphique ne nous dira rien sur quelles marques ont les scores “les plus élevés” en attributs. Une fois que vous avez compris comment créer et analyser les graphiques, l’analyse de correspondance est un outil puissant qui ignore les effets de dimensionnement de la marque pour fournir des informations puissantes et faciles à interpréter sur les relations entre et au sein des marques et leurs attributs applicables.

FAQ