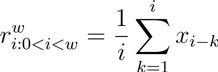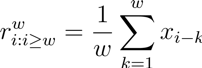Cálculos continuos en métricas de Widget
Acerca de los cálculos rotativos
Los cálculos continuos son un medio para aplicar una métrica sobre un conjunto de puntos de datos compuestos por múltiples períodos. Las opciones incluyen promedios móviles y métricas móviles.
Promedios móviles toma una serie de puntos, donde esos puntos pueden ser el resultado de cualquier tipo de cálculo métrico, y los promedia en una ventana de un tamaño específico.
Métricas continuas aplicar una métrica elegida utilizando todos los puntos de datos dentro de un tamaño de ventana especificado. A diferencia de los promedios móviles, utiliza todos los datos para producir una nueva métrica calculada.
Puede agregar promedios móviles y métricas móviles a los widgets del Tablero . Sin embargo, primero debes asegurarte de que el widget que estás usando sea compatible y que los datos mostrados estén desglosados por fecha.
Compatibilidad de Widget
Se pueden agregar cálculos continuos a cualquier widget que permita agregar métricas, además de una dimensión, fila o eje donde los datos se pueden desglosar por fecha.
Esto incluye lo siguiente:
Filtros de fecha aplicado a la página de tablero afectará los cálculos continuos.
Los cálculos rotativos son compatibles con ponderación.
Cálculos rodantes no puedo ser usado con prueba de significancia.
Cómo agregar una fecha de Desglose
A continuación se muestra un ejemplo de un desglose de fecha que se agrega a un widget de barra vertical.
- Haga clic para editar su widget.
- En el panel de edición del widget , haga clic en Agregar en el Eje X sección.
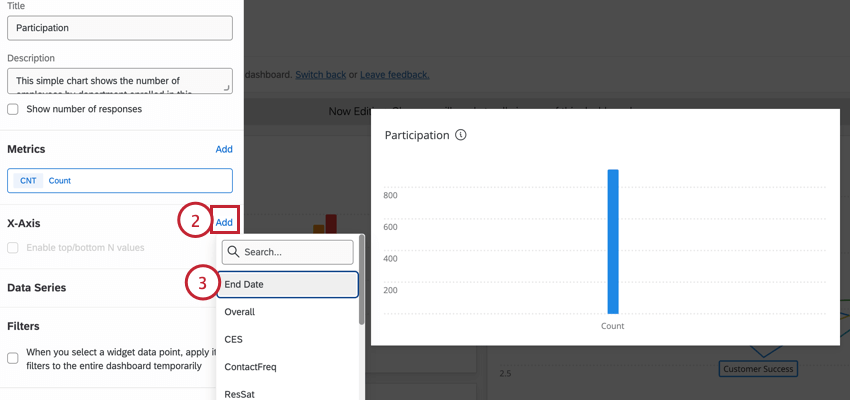
- Elige una Fecha campo.
Consejo Q: Puedes comprobar un campo tipo de campo en datos del Tablero sección del Tablero.
- Haga clic en el campo del eje x.
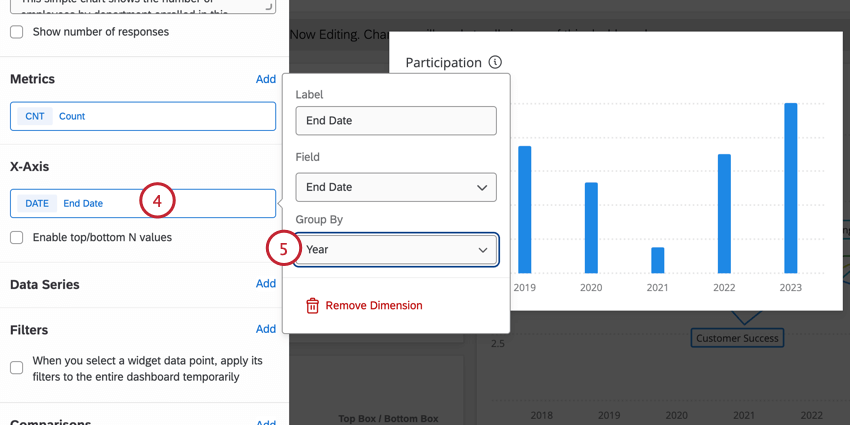
- Elija el período de tiempo en el que se agruparán sus datos. Puedes hacerlo por año, trimestre, mes, semana, día o automático.
Cómo agregar un promedio móvil o una métrica móvil a un Widget
- Utilice uno de los widgets compatibles y Desglosar los datos por fecha, como se explica en las secciones anteriores.
- Asegúrese de tener al menos una métrica. Si aún no ha agregado uno, haga clic en Agregar en el Métrico sección.
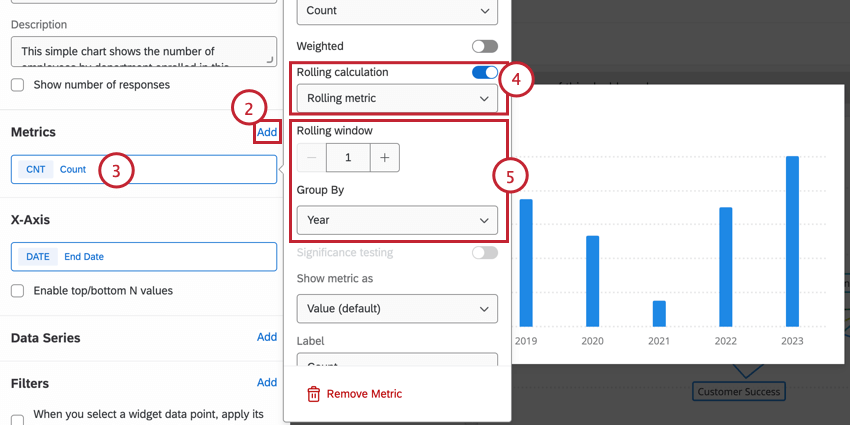 Consejo Q: Puedes elegir cualquier métrica que desees, como NPS o Promedio. El cálculo continuo aplicado se calculará en base a esta métrica. Sin embargo, los cálculos rotativos no son compatibles con métricas personalizadas.
Consejo Q: Puedes elegir cualquier métrica que desees, como NPS o Promedio. El cálculo continuo aplicado se calculará en base a esta métrica. Sin embargo, los cálculos rotativos no son compatibles con métricas personalizadas. - Haga clic en la métrica que agregó.
- Permitir Cálculo rodante y luego use el menú desplegable para elegir su cálculo, ya sea Promedio móvil o Métrica móvil.
- Seleccione el período de tiempo durante el cual desea que se realicen los cálculos. Puede escribir cualquier valor y elegir entre año, trimestre, mes, semana, día o automático, si así configura su desglose de fechas.
Cómo se calculan los promedios móviles
El promedio móvil toma “el promedio de los promedios”. Tomará cada valor métrico (que en sí mismo es el promedio de las respuestas de cada encuestado) dentro de una ventana específica y los promediará a lo largo del número de ventanas. Esto significa que el promedio resultante es independiente del tamaño de la muestra para cualquier período determinado.
El promedio móvil se implementa sobre las métricas que se permiten sobre valores escalares (valores numéricos). El algoritmo implementa esencialmente el siguiente conjunto de ecuaciones. Para el tamaño de ventana `w`:
Comportamiento para los datos actuales
El comportamiento predeterminado incluye el punto de datos actual de la ventana y utiliza el valor actual en el depósito para cada punto de datos.
Ejemplo: Supongamos que tenemos un conjunto de puntos de datos para una métrica (recuento, suma, promedio, etc.). Entonces digamos que usamos “promedio” para este ejemplo, con tamaño de ventana “2”.
| Fecha | 1/1/2018 | 1/2/2018 | 1/3/2018 | 1/4/2018 | 1/5/2018 | 1/6/2018 |
| Métrica original calculada | 10 | 6 | 11 | 2 | 9 | 14 |
| Media móvil | (10) / 2
= 5
|
(10 + 6) / 2
= 8 |
(6 + 11) / 2
= 8.5 |
(11 + 2) / 2
= 6.5 |
(2 + 9) / 2
= 5.5 |
(9 + 14) / 2
= 11.5 |
- El último punto de datos se considera incompleto y contribuirá a los cálculos del promedio móvil cuando tengamos un punto de datos para el 1/7/2018.
Comportamiento del promedio móvil para datos dispersos
Los datos representados arriba son un comportamiento definido según las ecuaciones mencionadas en el gráfico. Pero en un escenario del mundo real, los datos suelen ser escasos. Estos casos se denominan “puntos de datos faltantes” o “caso nulo”. En este caso solo existe el promedio sobre los elementos de la ventana. Si faltan elementos en la ventana, los promedios móviles no utilizarán los puntos de datos anteriores para completar la ventana.
Ejemplo:
| Fecha | 1/1/2018 | 1/2/2018 | 1/3/2018 | 1/4/2018 | 1/5/2018 | 1/6/2018 |
| Métrica original calculada | 10 | FALTANTE | 11 | FALTANTE | FALTANTE | 14 |
| Media móvil | (10) / 2 = 5 |
(10 + Nulo) / 1 = 10 |
(NULL + 11) / 1 = 11 |
(11 + NULO) / 1 = 11 |
(NULO + NULO) = NULO |
(NULL + 14) / 1 = 14 |
Cómo se calculan las métricas continuas
Las métricas continuas funcionan de la misma manera que las métricas normales, excepto que los datos utilizados pueden ampliarse más allá de un período, de manera continua. El comportamiento predeterminado incluye el punto de datos actual para la ventana que utiliza el valor actual en el depósito para cada punto de datos.
Las métricas móviles pueden considerarse como una “métrica móvil ponderada”. En este caso, “ponderado” significa que el valor de su métrica controla el tamaño de base en cada período de tiempo en la ventana, aplicando más peso a los períodos de tiempo de tamaño de base alto y menos peso a los períodos de tiempo de tamaño de base bajo.
Ejemplo: Supongamos que tenemos un conjunto de puntos de datos para una métrica (recuento, suma, promedio, etc.). Entonces digamos que usamos “promedio” para este ejemplo, con tamaño de ventana “2”.
| Fecha | 1/1/2018 | 1/2/2018 | 1/3/2018 | 1/4/2018 | 1/5/2018 | 1/6/2018 |
| Número original de puntos de datos | 12 | 17 | 20 | 10 | 15 | 25 |
| Suma de valores | 36 | 52 | 78 | 62 | 55 | 89 |
| Métrica con desplazamiento | 36 / 12 = 3 | (36 + 52) / (12 + 17) = 3.03 | (52 + 78) / (17 + 20) = 3.51 | (78 + 62) / (20 + 10) = 4.67 | (62 + 55) / (10 + 15) = 4.68 | (55 + 89) / (15 + 25) = 3.6 |
- Cada punto de datos siguiente obtiene el promedio de las sumas utilizando la cantidad de puntos de datos dentro del tamaño de ventana de dos.
COMPORTAMIENTO DE LA MÉTRICA ROLLAR PARA DATOS DISPERSOS
Los datos representados arriba son un comportamiento definido según las ecuaciones mencionadas en el gráfico. Pero en un escenario del mundo real, los datos suelen ser escasos. Estos casos se denominan “puntos de datos faltantes” o “caso nulo”. En este caso, la métrica todavía se calcula utilizando la cantidad de puntos de datos disponibles dentro de esa ventana.