Guía fácil de usar para la regresión lineal

¿Qué es la regresión?

Regresión estima una fórmula matemática que relaciona una o más variables de entrada con una variable de salida.

Por ejemplo, digamos que maneja un puesto de limonada y que está interesado en lo que impulsa los ingresos. Sus datos incluyen “Ingresos” de cada día, “Temperatura” alta, “Número de niños que caminaron por”, “Número de adultos que caminaron”, “Señalización” que utilizó ese día, y un “ingreso del competidor cercano”.

Piensa que “Temperatura” (una variable de entrada o explicativa) podría afectar a “Ingresos” (una variable de salida o respuesta). Cuando utiliza la regresión para analizar esta relación, puede producir esta fórmula:

Ingresos = 2,71 * Temperatura   –   35Esta

fórmula es útil por dos motivos.

En primer lugar, le permite entender una relación: los días más calurosos conducen a más “ingresos”. En particular, el 2,71 antes de “Temperatura” (llamado coeficiente) significa que por cada grado “Temperatura” sube, en promedio habrá $ 2,71 más “Ingresos”. Esta información podría llevarte a decidir no vender limonada en días fríos.

En segundo lugar, y en relación con ello, también puede ayudarle a realizar predicciones específicas. Si la “Temperatura” es 24, podría estimar que desde…

Ingresos = 2,71 * Temperatura   –   35
Ingresos = 2,71 * 24   –   35
Ingresos = 30

…tendrá alrededor de 30 $ en “Ingresos”. Esa información podría ser útil para saber si podrá realizar un pago ese día, asumiendo que está seguro de que su modelo es preciso.

Ahora veremos el proceso de creación de esta ecuación de regresión.

Preparación para crear un modelo de regresión

1. Piensa en la teoría de tu regresión

Una vez que haya elegido una variable de respuesta, “Ingresos“ planteará la hipótesis de cómo se pueden relacionar varias entradas con ella. Por ejemplo, puede pensar que una “temperatura” más alta dará lugar a mayores “ingresos”, puede no estar seguro de cómo afectarán los “ingresos” a varias señales y puede creer que las “ventas de la competencia” se ven afectadas por la “temperatura” pero no tienen ningún impacto en su puesto de limonada.

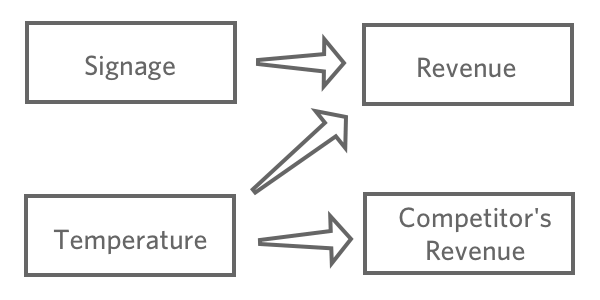
El objetivo de la regresión suele ser comprender la relación entre varias entradas y una salida, por lo que en este caso probablemente decidiría crear un modelo que explique “Ingresos” con “Temperatura” y “Señalización” (también dicho como “predecir Ingresos de Temperatura y Señalización“, incluso si está más interesado en la explicación que en la predicción real).

Probablemente no incluiría “Ventas de competidor” en su regresión. Es probable que esté correlacionado con “Ingresos”, pero no le precede en la cadena causal, por lo que incluirla confundiría su modelo.

2. “Describa” todas las variables que podrían ser útiles para su modelo

Comience describiendo la variable de respuesta, en este caso “Ingresos”, y obteniendo una buena idea. Haga lo mismo para las variables explicativas.

Tenga en cuenta que tienen una forma como esta…

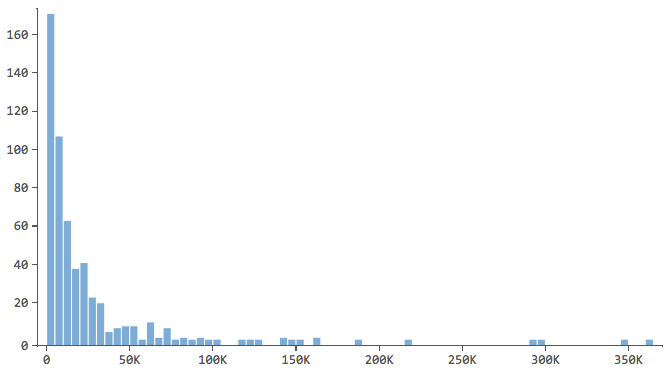
…donde la mayoría de los datos están en las primeras ubicaciones del histograma. Estas variables requerirán una atención especial más adelante.

3. “Relacionar” todas las variables explicativas posibles a la variable de respuesta

Stats iQ ordenará los resultados por la fortaleza de la relación estadística. Eche un vistazo a los resultados y descubra qué variables están relacionadas con “Ingresos” y cómo.

Si ya tiene una buena idea de qué variables deberían dirigir teóricamente el resultado (por ejemplo, de documentos académicos anteriores), debe omitir este paso. Pero si su análisis es un poco más exploratorio (como una encuesta de cliente), este es un paso útil e importante.

4. Comenzar a construir la regresión

Crear un modelo de regresión es un proceso iterativo. Recorrerá las tres etapas siguientes tantas veces como sea necesario.

Las tres etapas de la construcción de un modelo de regresión

Etapa 1: Sumar o restar una variable

Uno por uno, empiece a añadir en variables que sus análisis anteriores indicaban estaban relacionados con “Ingresos” (o añada variables que tenga un motivo teórico para añadir). Ir uno a uno no es estrictamente necesario, pero facilita la identificación y resolución de problemas a medida que avanza y lo ayuda a hacerse una idea del modelo.

Supongamos que empieza por predecir “Ingresos” con “Temperatura”. Encuentra una relación fuerte, evalúa el modelo y lo encuentra satisfactorio (más detalles en un minuto).

Ingresos = 2,71 * Temperatura   –   35A

continuación, añada “Número de niños que pasearon” y ahora su modelo de regresión tiene dos términos, ambos son predictores estadísticamente significativos. Así:

Ingresos = 2.5 * Temperatura   +   0.3 * NumberOfChildrenWhoWalkedBy   –   12Luego

se añade “Número de adultos que caminaron”, y los resultados del modelo ahora muestran que “Número de adultos” es estadísticamente significativo en el modelo, pero “Número de niños” ya no lo es. Normalmente, eliminaría “Número de elementos inferiores” del modelo. Ahora tenemos:

Ingresos = 2,6 * Temperatura   +   0,4 * NúmeroDeAdultosWhoWalkedBy   –   14

Esto significa que “Número de adultos” es el mejor predictor de “Ingresos”; es decir, si sabes cuántos adultos vienen, saber cuántos niños vienen no agrega ninguna información nueva – no ayuda a predecir las ventas.

Tal vez piensen atrás y recuerden que los niños en realidad no compran tu limonada, así que tiene sentido que esa variable no pertenezca al modelo.

Sin embargo, ¿por qué fue estadísticamente significativo en el primer modelo? Probablemente porque “Número de niños” está correlacionado con “Número de adultos“, y dado que “Número de adultos” aún no estaba en el modelo, “Número de niños” estaba actuando como un aproximado aproximado de “Número de adultos”.

Interpretar los resultados de la regresión requiere un buen juicio, y el hecho de que una variable sea estadísticamente significativa no significa que sea realmente causal. Pero añadiendo y restando variables cuidadosamente, notando cómo cambia el modelo y siempre pensando en la teoría detrás de su modelo, puede separar las relaciones interesantes en sus datos.

Etapa 2: Evaluar el modelo

Cada vez que agregue o reste una variable, debe evaluar la precisión del modelo observando su R cuadrado (^R2), AICR y sus gráficos residuales. Cada vez que modifique el modelo, compare los nuevos diagramas R cuadrado, AICR y residual con los anteriores para determinar si el modelo ha mejorado o no.

R cuadrado (^R2)

La métrica numérica para cuantificar la precisión de predicción del modelo se conoce como r-cuadrado, que se encuentra entre cero y uno. Un cero significa que el modelo no tiene ningún valor predictivo y uno significa que el modelo lo predice todo a la perfección.

Por ejemplo, el modelo de la izquierda es más preciso que el de la derecha; es decir, si sabe “Temperatura”, tiene una conjetura bastante buena en cuanto a qué “Ingresos” estará a la izquierda, pero no realmente a la derecha.

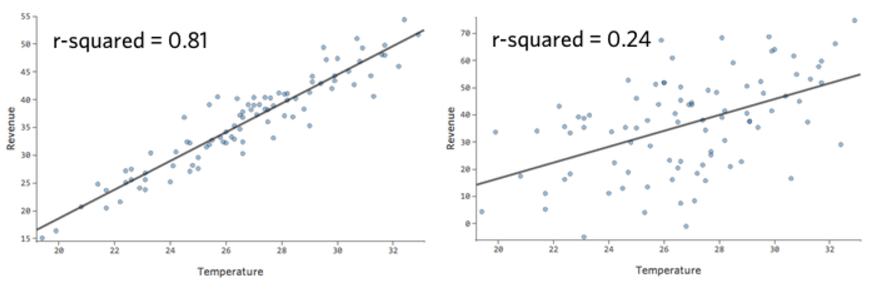
No existe una definición fija de un r-cuadrado “bueno”. En algunas opciones puede ser interesante ver cualquier efecto, mientras que en otras su modelo puede ser inútil a menos que sea muy preciso.

Cada vez que añada una variable, r-cuadrado subirá, por lo que lograr el R-cuadrado más alto posible no es el objetivo; más bien, desea equilibrar la precisión del modelo (r-cuadrado) con su complejidad (generalmente, el número de variables que contiene).

AICR

AICR es una métrica que equilibra la precisión con la complejidad: una mayor precisión conduce a mejores puntuaciones, y la complejidad añadida (más variables) lleva a peores puntuaciones. El modelo con el AICR inferior es mejor.

Tenga en cuenta que la métrica AICR solo es útil para comparar AICR de modelos que tienen el mismo número de filas de datos yla misma variable de salida.

Intervalos de predicción

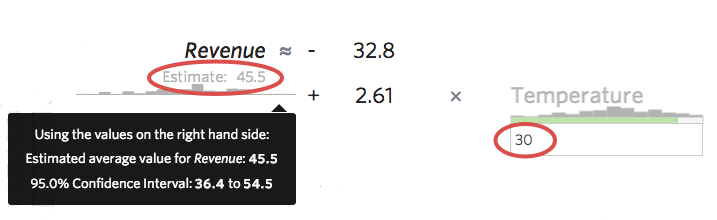
Otra forma útil de entender la precisión del modelo es incluir valores de muestra en la fórmula y ver el intervalo de predicción que calcula Stats iQ. Por ejemplo, si pega el número 30 en la fórmula, Stats iQ le dirá que el valor previsto es 45,5, pero el intervalo de confianza del 95% es de 36,4 a 54,5, lo que significa que podría estar un 95% seguro de que si mañana resultara ser de 30 grados, obtendría entre 36,40 $ y 54,50 $ en “Ingresos”. Se podía imaginar un modelo más preciso donde el intervalo de predicción era una banda ajustada como $44 a $48, o uno menos preciso donde el intervalo era ancho, como $20 a $72.

Este enfoque solo es útil cuando sus diagramas residuales tienen un aspecto saludable (ver más abajo); de lo contrario, serán imprecisos.

Gráficos residuales

Los residuos son la herramienta de diagnóstico principal para evaluar y mejorar la regresión, por lo que hay una sección completamente separada sobre la interpretación de los residuos para mejorar su modelo. Aprenderá o actualizará su memoria sobre qué son los residuos, cómo utilizarlos para evaluar y mejorar el modelo y cómo pensar en la precisión que necesita que sea su modelo.

Le recomendamos que lo lea en su totalidad, ya que cubrirá todo lo demás que necesita para producir un gran modelo. Pero siempre se puede volver sobre ello, por supuesto.

Etapa 3: Modificar el modelo según corresponda

Si su evaluación del modelo resulta satisfactoria, puede terminar o puede volver a la Etapa 1 e introducir más variables.

Si su evaluación encuentra que falta el modelo, utilizará las alertas de Stats iQ y la sección de diagnóstico residual para solucionar los problemas.

A medida que modifica el modelo, tenga en cuenta continuamente el cambio de R cuadrado, AICR y diagnósticos residuales, y decida si los cambios que está realizando están ayudando o perjudicando a su modelo.

Preguntas frecuentes