Cómo interpretar diagramas residuales para mejorar su regresión
Al ejecutar una regresión, Stats iQ calcula y traza automáticamente los valores residuales para ayudarle a comprender y mejorar el modelo de regresión. Lea a continuación para conozca todo lo que necesita saber sobre la interpretación de residuos (incluidas definiciones y ejemplos).
Observaciones, predicciones y valores residuales
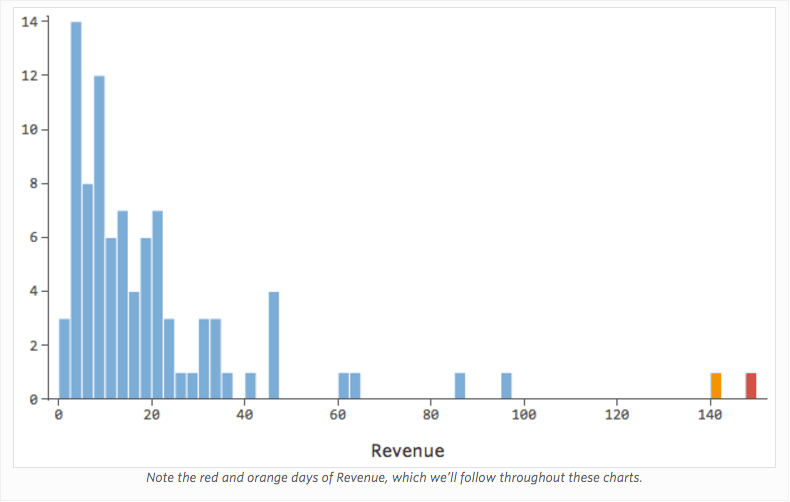
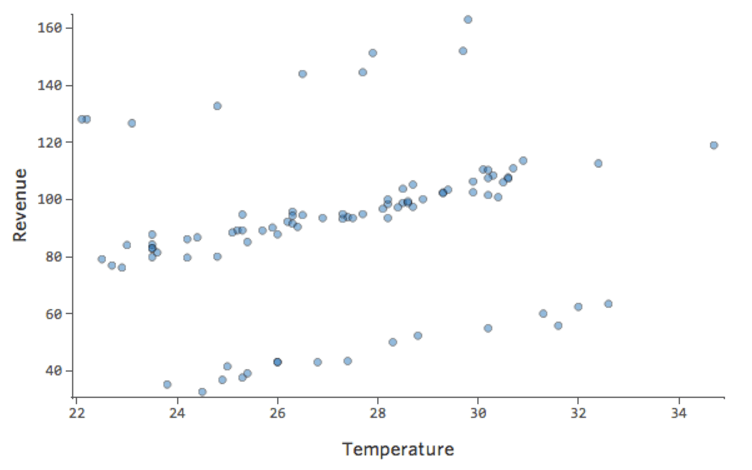
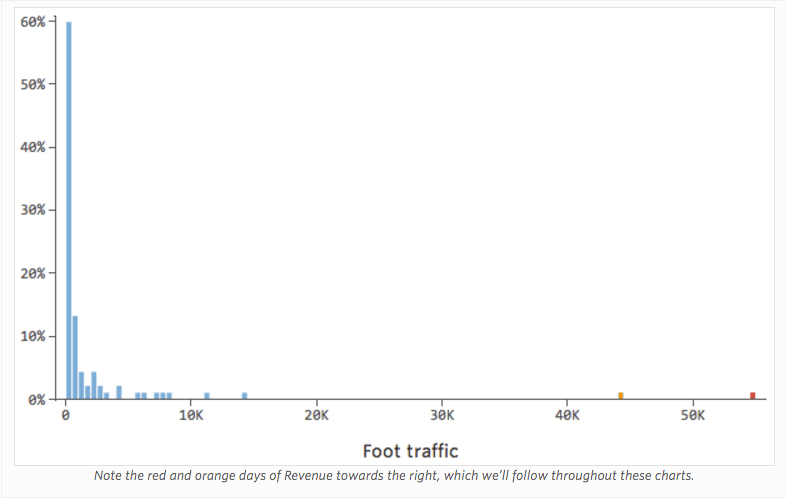
Para demostrar cómo interpretar los valores residuales, usaremos un conjunto de datos del stand de limonada, donde cada fila representa la “Temperatura” y los “Ingresos” del día.
| Temperatura (Celsius) | Ingresos |
|---|---|
| 28,2 | $ 44 |
| 21,4 | $ 23 |
| 32,9 | $ 43 |
| 24,0 | $ 30 |
| etc. | etc. |
La ecuación de regresión que describe la relación entre “Temperatura” e “Ingresos” es:
Ingresos = 2,7 * Temperatura – 35
Supongamos que un día en el puesto de limonadas hizo 30,7° y los ingresos fueron de $ 50. Ese 50 es su resultado observado o real , el valor real.
Entonces, si insertamos 30,7 como valor para “Temperatura”…
Ingresos = 2,7 * 30,7 – 35
Ingresos = 48
…obtenemos $ 48. Ese es el valor previsto para ese día, también conocido como el valor para “Ingresos”, la ecuación de regresión lo habría predicho en base a la “Temperatura”.
Su modelo no siempre es perfecto bien, por supuesto. En este caso, la predicción falla de 2; esa diferencia, 2, se llama residual. El valor residual es el resto que queda cuando se resta el valor previsto del valor observado.
Residual = observado – previsto
Ahora puede imaginar que cada fila de datos tiene un valor previsto y también un valor residual.
| Temperatura (Celsius) |
Ingresos (observado) |
Ingresos (previsto) |
Residual (observado – previsto) |
|---|---|---|---|
| 28,2 | $ 44 | $ 41 | $ 3 |
| 21,4 | $ 23 | $ 23 | $ 0 |
| 32,9 | $ 43 | $ 54 | 11 |
| 24,0 | $ 30 | $ 29 | $ 1 |
| etc. | etc. | etc. | etc. |
Vamos a utilizar los valores observados, previstos y residuales para evaluar y mejorar el modelo.
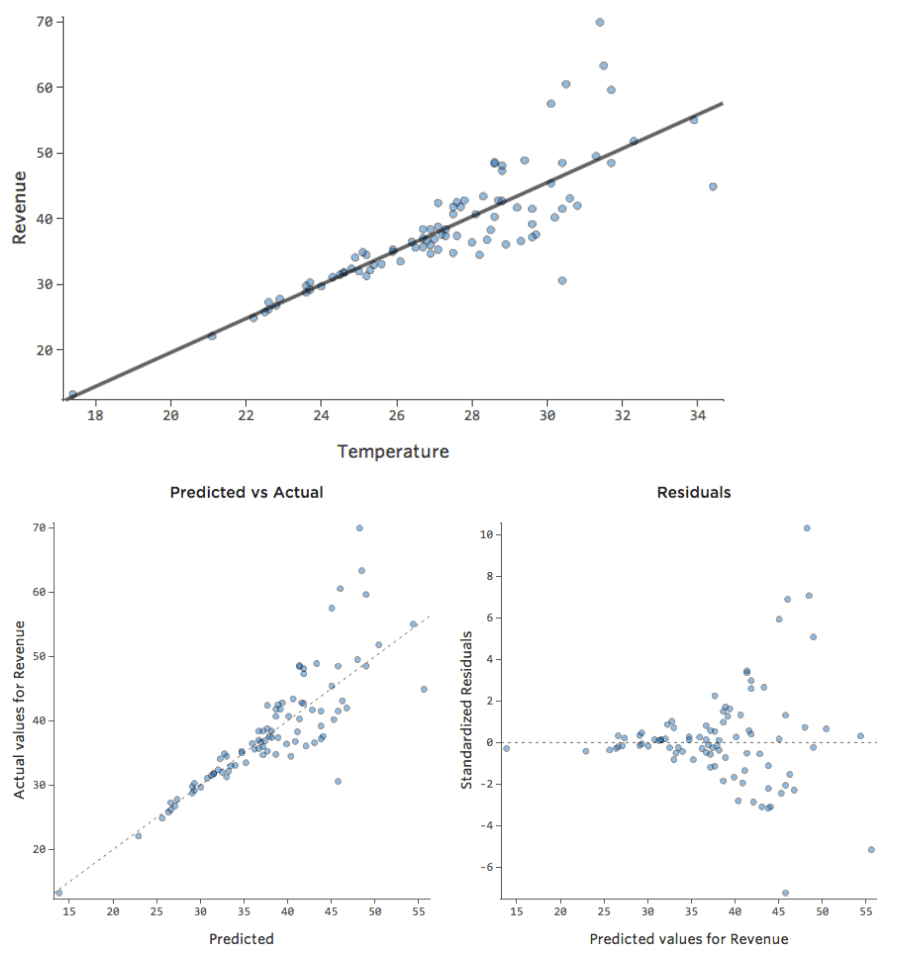
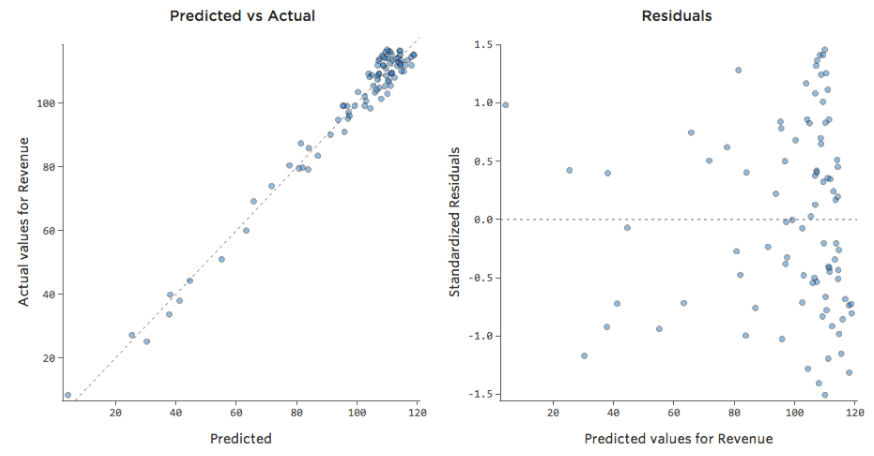
Comprensión de la precisión con Observados vs. Previstos
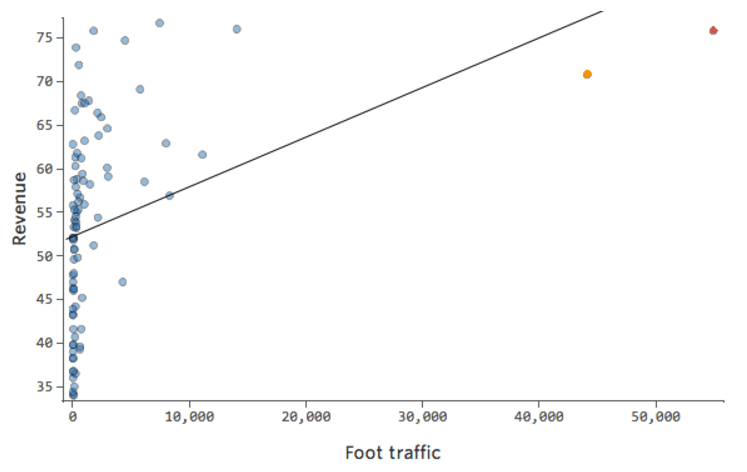
En un modelo simple como este, con solo dos variables, puede obtener una idea de cuán preciso es con solo relacionar la “Temperatura” con los “Ingresos”. Aquí está la misma ejecución de regresión en dos puestos de limonada diferentes, una donde el modelo es muy preciso, una en la que el modelo no lo es:
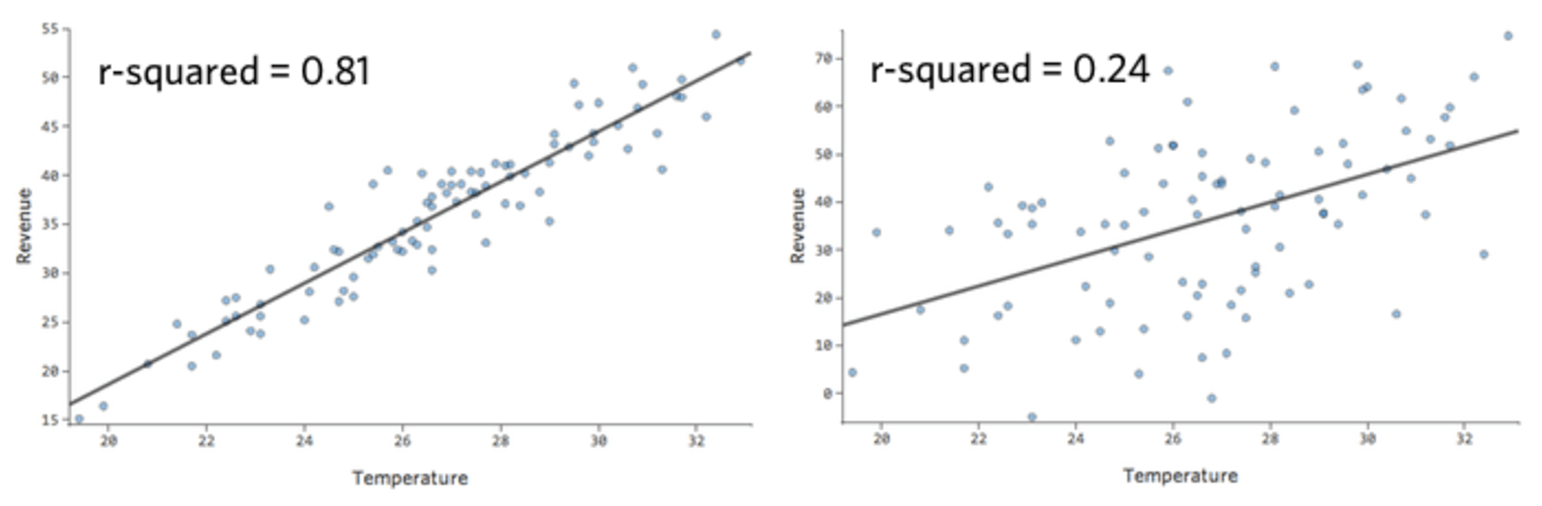
Está claro que para ambos puestos de limonada, con una “Temperatura” más alta tienen mayores “Ingresos”. Pero a una determinada “Temperatura”, podría ayudarnos a pronosticar los “Ingresos” del puesto de la izquierda con mayor precisión respecto a los de la derecha, lo que significa que el modelo es mucho más preciso.
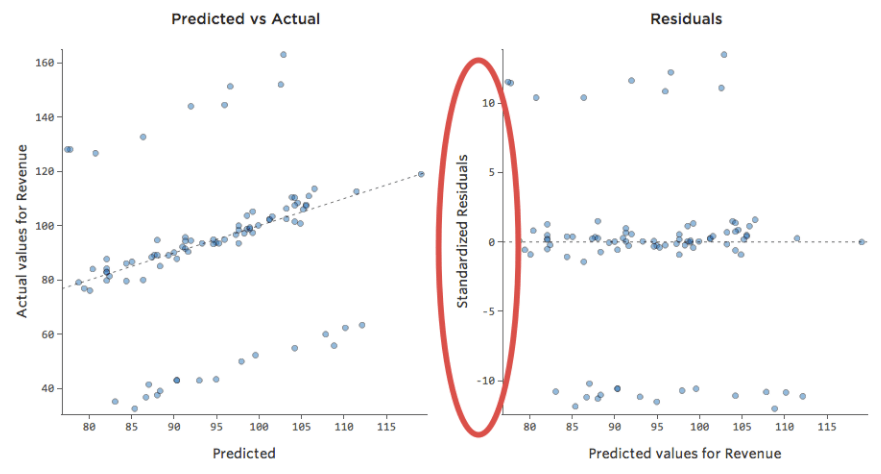
Pero la mayoría de los modelos tienen más de una variable explicativa y no es práctico representar más variables en ese tipo de gráfico. Por lo tanto, vamos a representar los valores previstos frente a los valores observados para estos mismos conjuntos de datos.
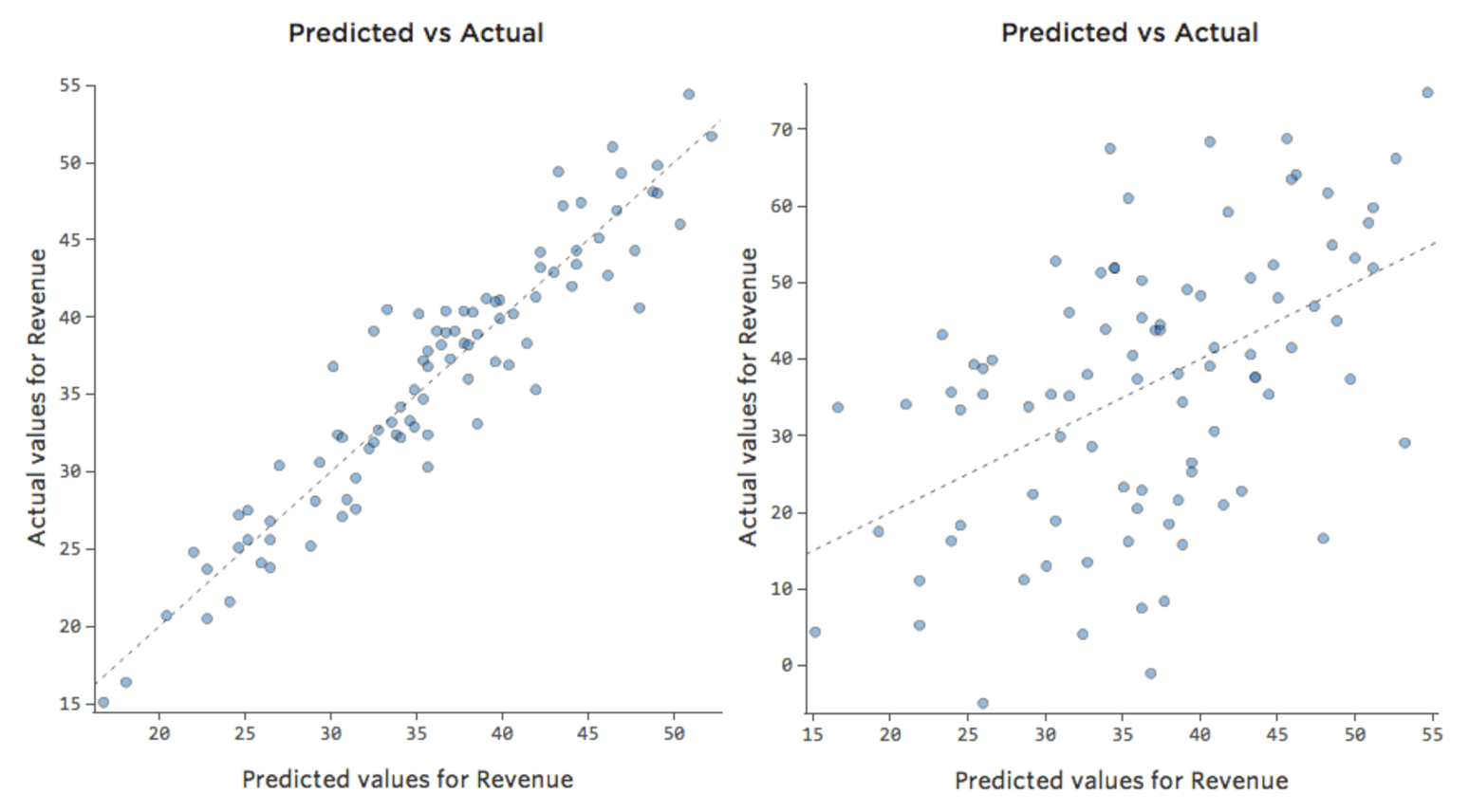
De nuevo, el modelo para el gráfico de la izquierda es muy preciso; hay una fuerte correlación entre las predicciones del modelo y sus resultados reales. Por el contrario, el modelo para el gráfico de la derecha no funciona porque las predicciones no son muy buenas.
Tenga en cuenta que estos gráficos analizan la “Temperatura”frente a los “Ingresos” que se encuentran arriba, pero el eje X predice los “Ingresos” en lugar de la “Temperatura”. Ese resultado es común cuando la ecuación de regresión solo tiene una variable explicativa. Sin embargo, tendrá varias variables explicativas con mayor frecuencia, y los gráficos tendrán un aspecto muy diferente respecto al diagrama de una variable explicativa vs. “Ingresos”.
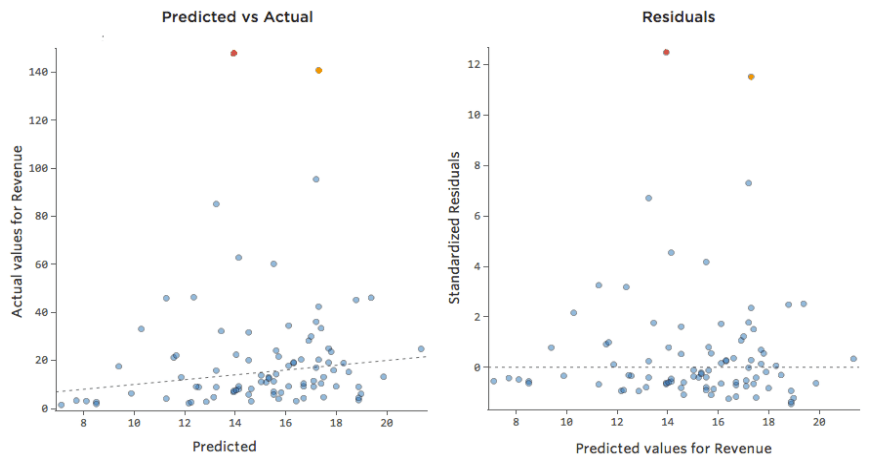
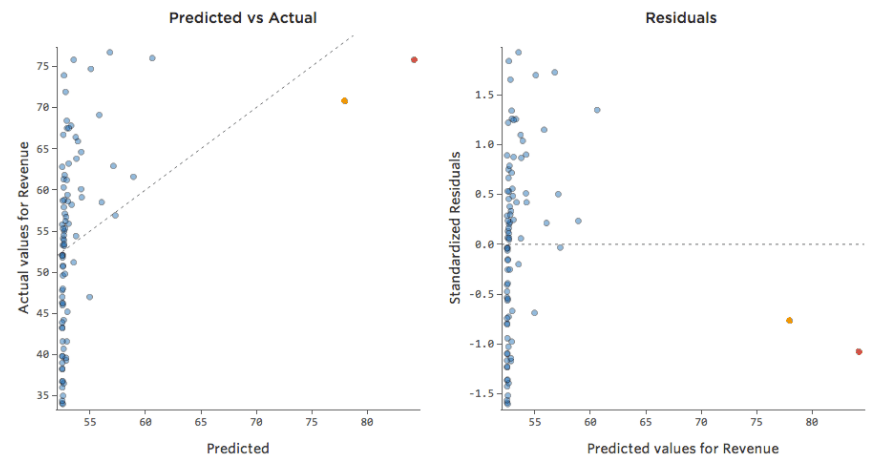
Examinar datos Previstos vs. Residual (“El diagrama residual”)
A pesar de que la forma más útil de trazar los valores residuales es con los valores previstos en el eje X y los valores residuales en el eje Y, no siempre es así.
(Stats iQ presenta los residuos como residuos estandarizados, lo que significa que cada diagrama residual que observa con cualquier modelo está en el mismo eje Y estandarizado).
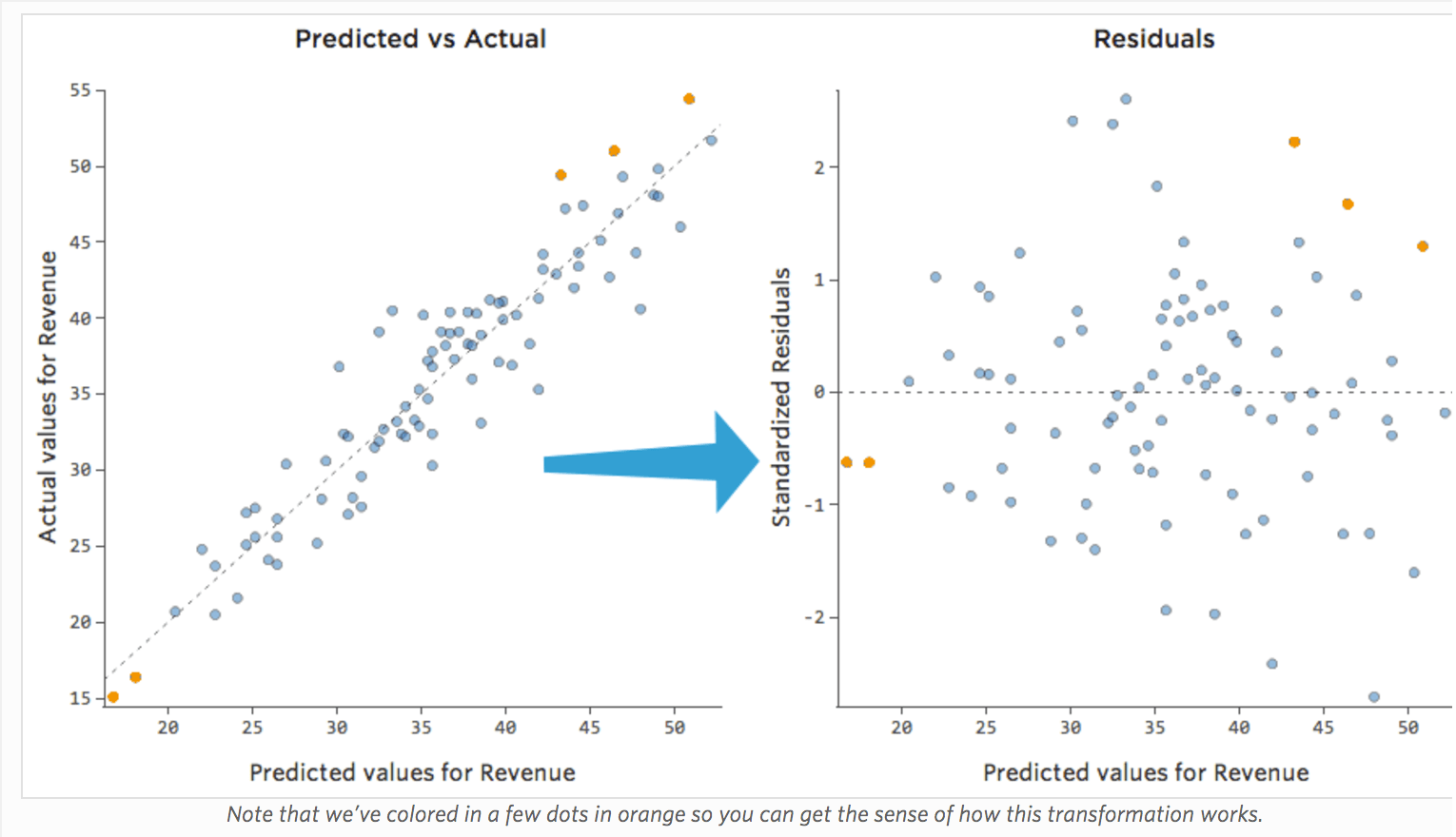
En el diagrama de la derecha, cada punto es un día, donde la predicción realizada por el modelo está en el eje X y la precisión de la predicción está en el eje Y. La distancia desde la línea en 0 es lo mala que era la predicción para ese valor.
Dado que…
Residual = observado – previsto
…los valores positivos para el residual (en el eje Y) significan que la predicción era demasiado baja, y los valores negativos significan que la predicción era demasiado alta; 0 significa que la estimación era exactamente correcta.
Idealmente, el diagrama de los residuos tiene el siguiente aspecto:
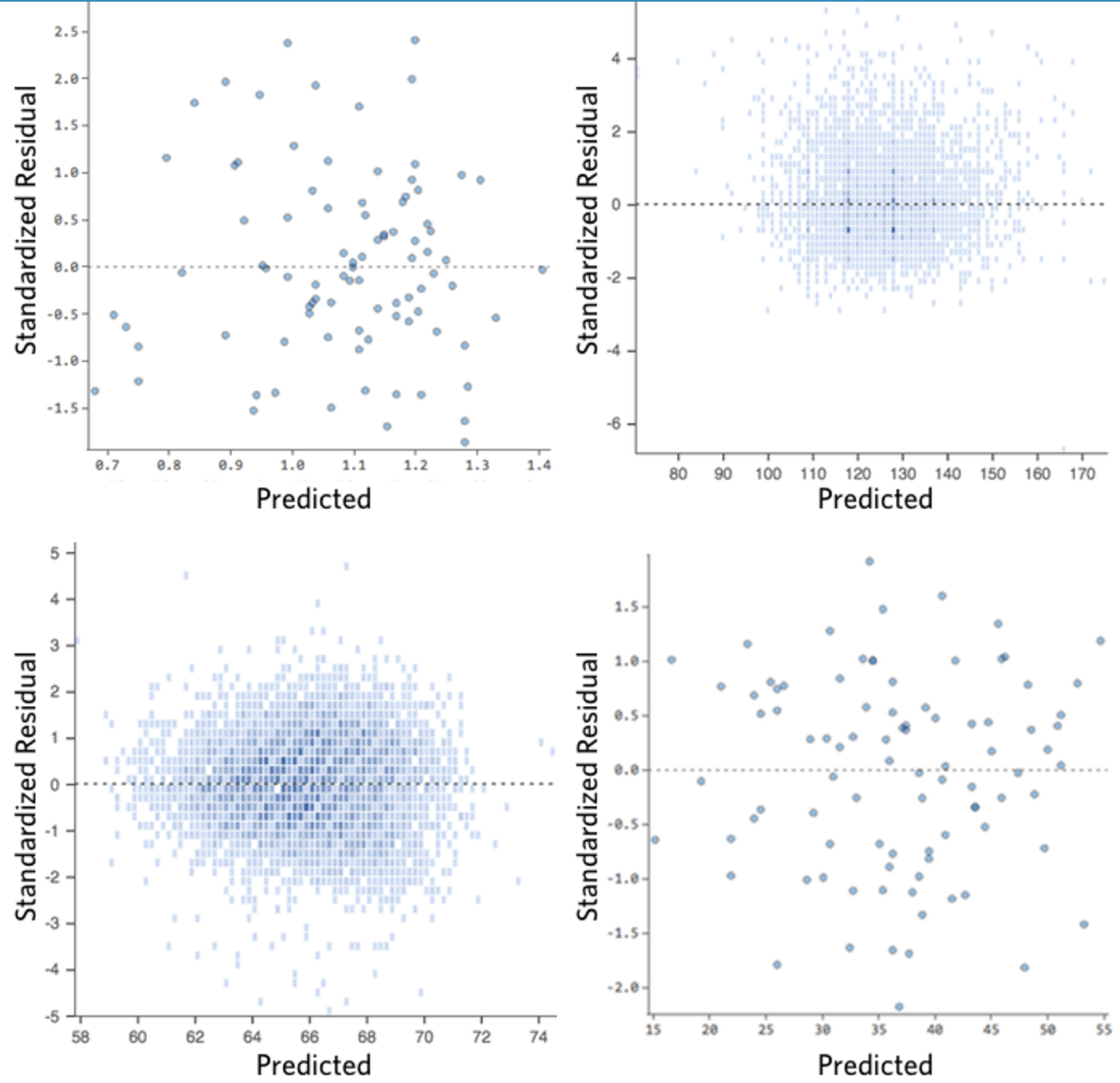
Es decir,
(1) se distribuyen de manera bastante simétrica, tendiendo a agruparse hacia la mitad del diagrama.
(2) se agrupan alrededor de los dígitos individuales inferiores del eje Y (por ejemplo, 0,5 o 1,5, no 30 o 150).
(3) en general, no hay patrones claros.
Estos son algunos diagramas residuales que no cumplen con esos requisitos:
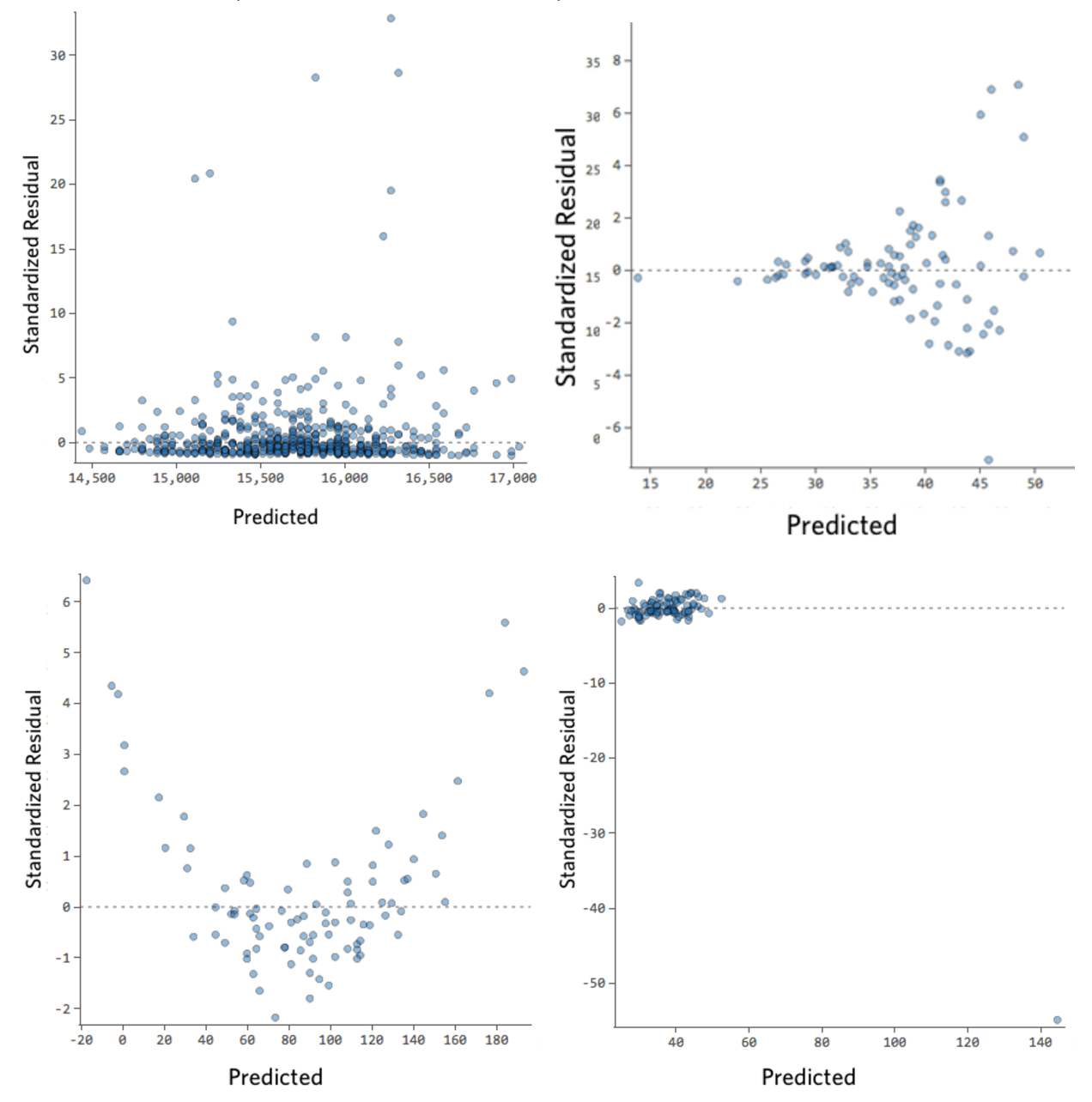
Estos diagramas no se distribuyen uniformemente verticalmente, tienen un valor atípico o tienen una forma clara para ellos.
Si puede detectar un patrón o una tendencia claros en sus residuos, su modelo tendrá un margen de mejora.
A breve, analizaremos el por qué y qué hacer al respecto.
Diagrama residual Q-Q normal:
Haga clic en Mostrar diagrama residual Q-Q normal para visualizar un diagrama Q-Q que evalúa la distorsión de datos y el ajuste de modelo. Este gráfico muestra los valores residuales estandarizados en el eje y y los cuantiles teóricos en el eje X.
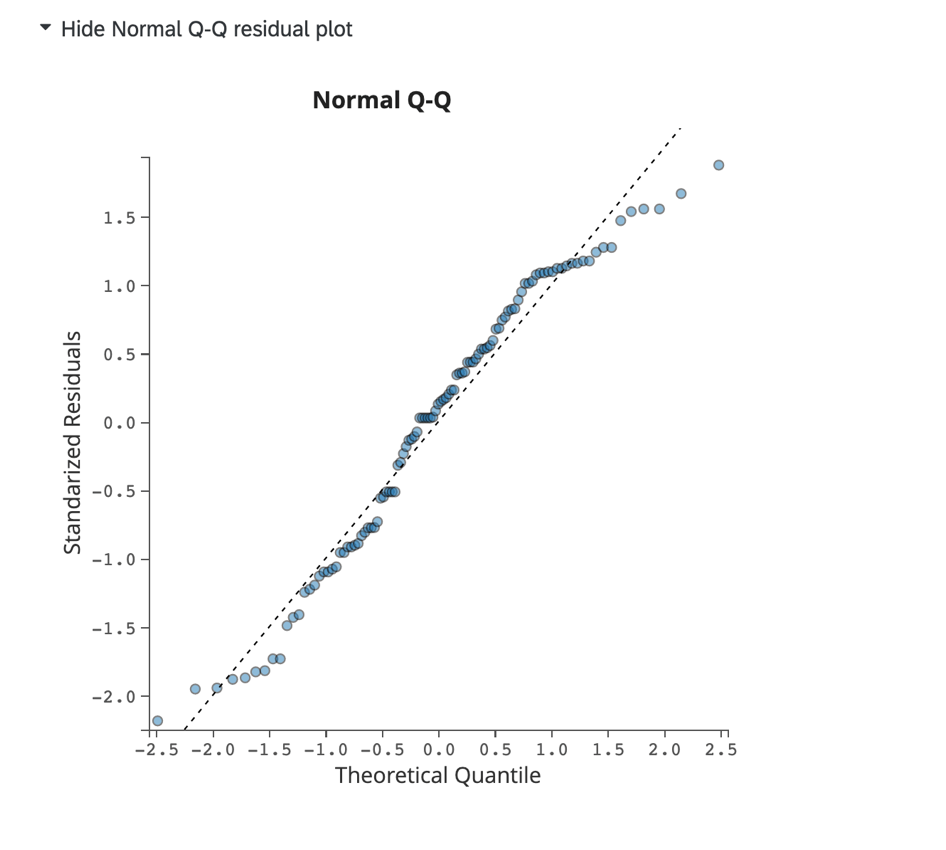 Los datos que se alinean estrechamente con la línea de puntos indican una distribución normal. Si los puntos se sesgan drásticamente desde la línea, podría considerar ajustar su modelo añadiendo o eliminando otras variables en el modelo de regresión.
Los datos que se alinean estrechamente con la línea de puntos indican una distribución normal. Si los puntos se sesgan drásticamente desde la línea, podría considerar ajustar su modelo añadiendo o eliminando otras variables en el modelo de regresión.
¿Qué tan importante es que mi modelo sea perfecto?
¿Cuánto le debería preocupar que su modelo no sea perfecto, si sus residuos parecen un poco insaludables? Depende de usted.
Si está presentandop su tesis en física de partículas, probablemente quiera asegurarse de que su modelo sea lo más preciso posible humanamente. Si está tratando de realizar un análisis rápido y básico del puesto de limonada de su sobrino, un modelo menos perfecto podría ser lo suficientemente bueno para responder cualquier pregunta que tenga (por ejemplo, si la “Temperatura” parece afectar a los “Ingresos”).
La mayoría de las veces un modelo decente es mejor que ninguno. Por lo tanto, tome su modelo, intente mejorarlo y, luego, decida si la precisión es lo suficientemente buena como para que sea útil para sus objetivos.
Ejemplos de diagramas residuales y sus diagnósticos
Si tiene la seguridad de qué es un residuo, tómese cinco minutos para leer lo anterior y luego regrese aquí.
Debajo hay una galería de diagramas residuales poco saludables. Su residual puede parecerse a un tipo específico de abajo, o alguna combinación.
Si el suyo se parece a una de las siguientes opciones, haga clic en el valor residual para comprender lo que está sucediendo y aprender a solucionarlo.
(A lo largo de todo el proceso usaremos los “Ingresos” de un puesto de limonada frente a la “Temperatura” del día como conjunto de datos de ejemplo).
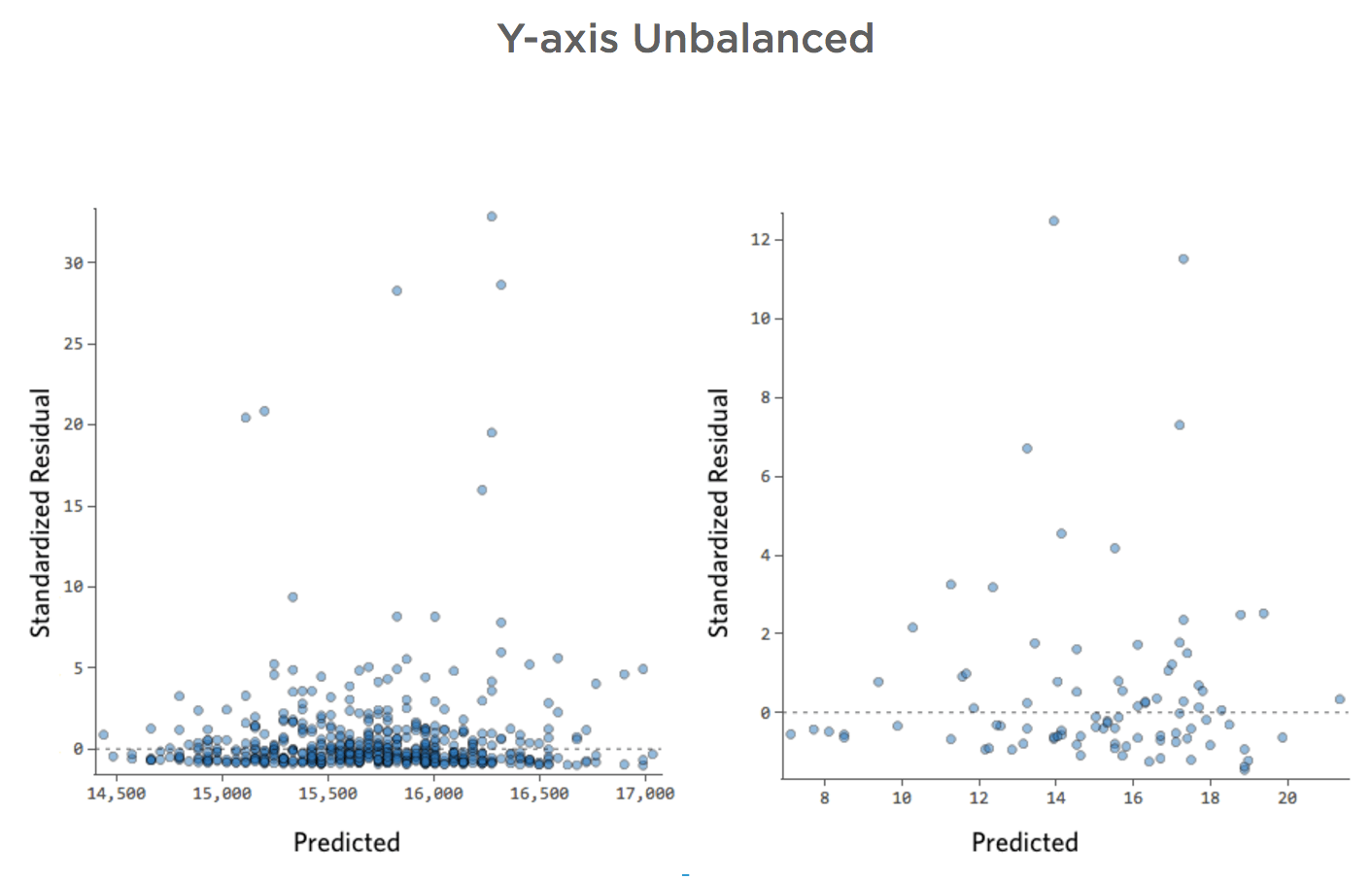
Eje Y desequilibrado
- Muestra detalles sobre este diagrama y cómo solucionarlo.
-
Problema
Imagine que, por la razón que sea, su puesto de limonada suele tener bajos ingresos, pero de vez en cuando obtiene unos días de ingresos muy altos, de modo que “Ingresos” se ve de esta manera…
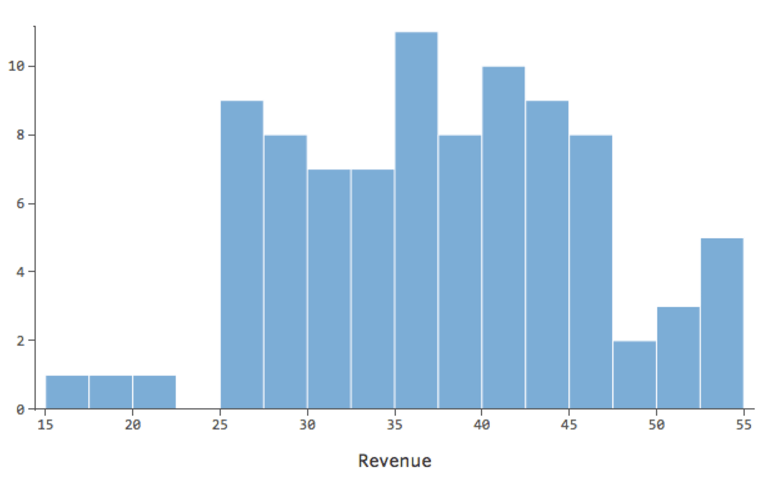
…en vez de algo más simétrico y con forma de campana como este:
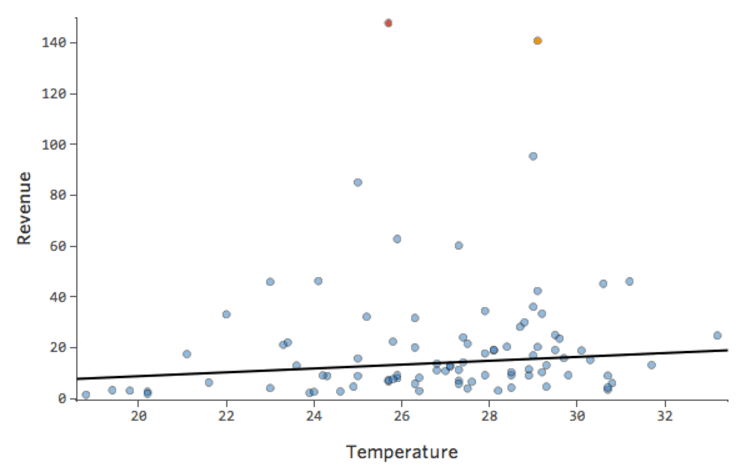
Así que “Temperatura” vs. “Ingresos” podría ser así, con la mayoría de los datos agrupados en la parte inferior…
La línea negra representa la ecuación del modelo, la predicción del modelo de la relación entre “Temperatura” e “Ingresos”. Mire en la parte superior de cada predicción hecha por la línea negra para una cierta “Temperatura” dada (por ejemplo, con una “Temperatura” de 30, se preveen “Ingresos” de 20). Puede ver que la mayoría de los puntos están por debajo de la línea (es decir, la predicción era demasiado alta), pero algunos puntos están muy por encima de la línea (es decir, la predicción era demasiado baja).
Traduciendo esos mismos datos a los diagramas de diagnóstico, la mayoría de las predicciones de la ecuación son demasiado altas, y entonces algunas serían muy bajas.
Implicaciones
Esto casi siempre significa que su modelo puede ser mucho más preciso. La mayoría de las veces verá que el modelo era direccionalmente correcto, pero bastante impreciso en relación con una versión mejorada. No es raro solucionar un problema como este y, en consecuencia, ver el salto del cuadrado R del modelo de 0,2 a 0,5 (en una escala de 0 a 1).
Cómo arreglarlo
- La solución a esto es casi siempre transformar sus datos, normalmente la variable de respuesta.
- También es posible que su modelo carezca de una variable.
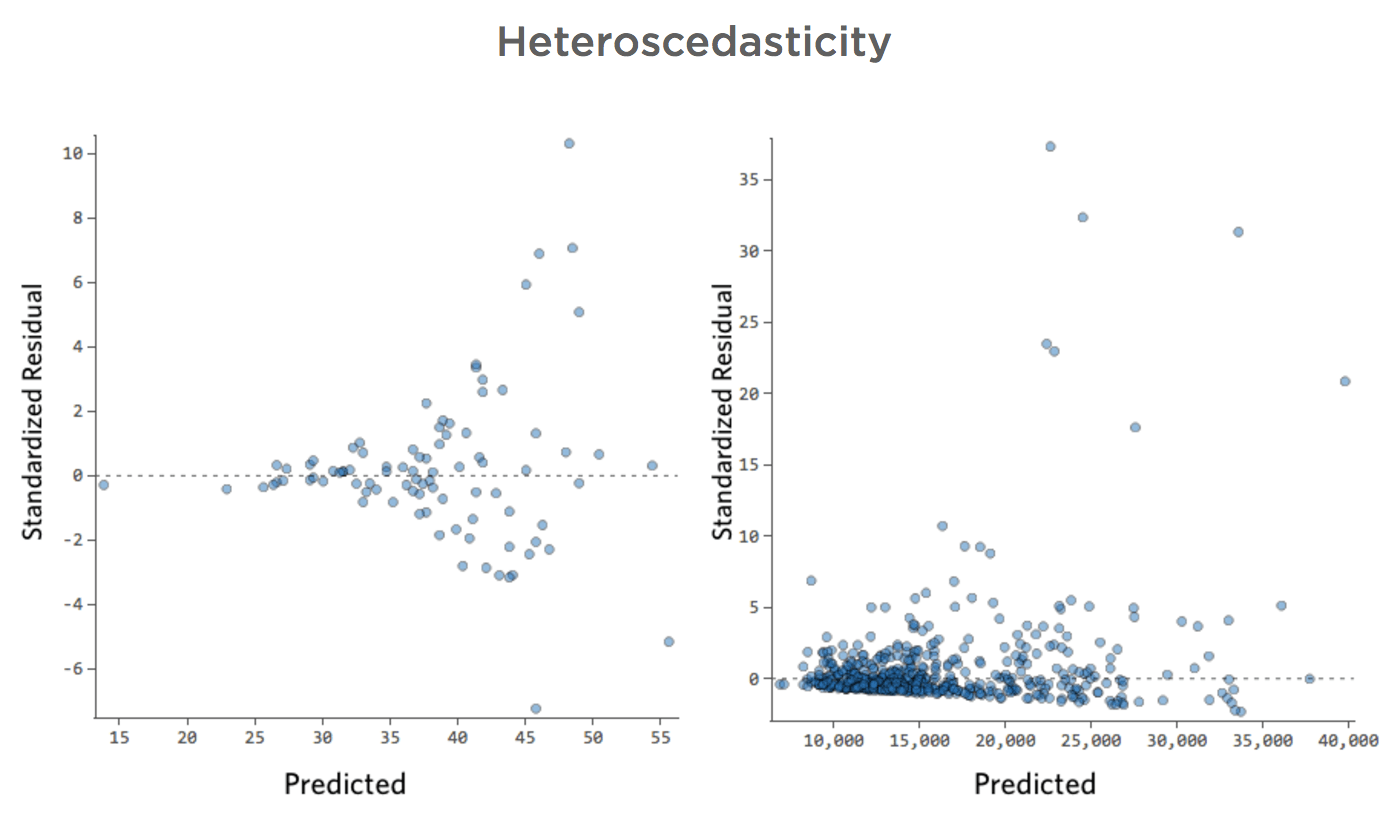
Heteroscedasticidad
- Muestra detalles sobre este diagrama y cómo solucionarlo.
-
Problema
Estos diagramas muestran “heteroscedasticidad”, lo que significa que los residuos se hacen más grandes a medida que la predicción se mueve de pequeño a grande (o de grande a pequeño).
Imagine que en los días fríos, la cantidad de ingresos es muy consistente, pero en días más calurosos, a veces los ingresos son muy altos y a veces son muy bajos.
Vería diagramas como estos:
Implicaciones
Esto no crea un problema de forma inherente, pero a menudo es un indicador de que su modelo puede mejorar.
La única excepción aquí es que si el tamaño de la muestra es inferior a 250 y no puede solucionar el problema utilizando lo siguiente, sus valores P pueden ser un poco más altos o más bajos de lo que deberían ser, por lo que posiblemente una variable que esté justo en el borde de importancia puede terminar erróneamente en el lado incorrecto de ese borde. Sin embargo, sus coeficientes de regresión (el número de unidades “Ingresos” cambia cuando “Temperatura” sube a uno) seguirán siendo precisos.
Cómo arreglarlo
- La solución más frecuente es transformar una variable.
- A menudo la heteroscedasticidad indica que falta una variable.
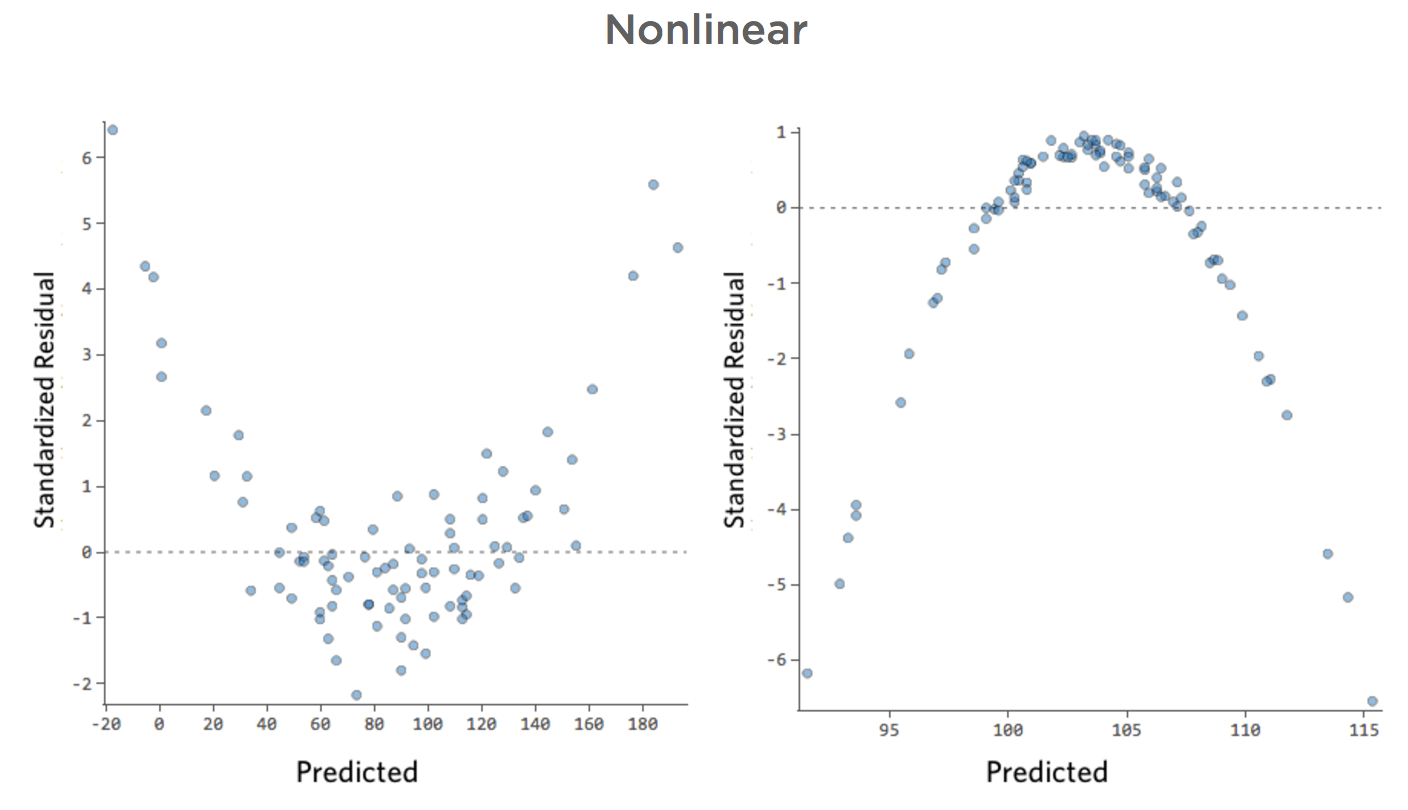
No lineal
- Muestra detalles sobre este diagrama y cómo solucionarlo.
-
Problema
Imagine que es difícil vender limonada en días fríos, fácil de venderla en días cálidos y difícil de venderla en días muy calurosos (tal vez porque nadie sale de su casa en esos días).
Ese diagrama se vería así:
El modelo, representado por la línea, es terrible. Las predicciones serían alternativas, lo que significa que su modelo no representa con precisión la relación entre “Temperatura” e “Ingresos”.
En consecuencia, los residuos tendrían el siguiente aspecto:
Implicaciones
Si su modelo está muy alejado, como en el ejemplo anterior, sus predicciones no tendrán ningún valor (y verá un cuadrado R muy bajo, como el 0,027 de arriba).
Otras veces, un ajuste ligeramente inferior al óptimo le dará un buen sentido general de la relación, incluso si no es perfecto, como el siguiente:
Ese modelo parece bastante preciso. Si observa de cerca (o si observa los residuos), puede decir que existe un patrón: los puntos están en una curva que la línea no coincide del todo.
¿Es eso importante? Depende de usted. Si comprende rápidamente la relación, su línea recta es una aproximación bastante decente. Si va a utilizar este modelo para la predicción y no para la explicación, el modelo más preciso posible probablemente tendría en cuenta esa curva.
Cómo arreglarlo
- A veces, patrones como este indican que una variable debe transformarse.
- Si el patrón es realmente tan claro como estos ejemplos, probablemente necesite crear un modelo no lineal (no es tan difícil como parece).
- O, como siempre, es posible que falte una variable.
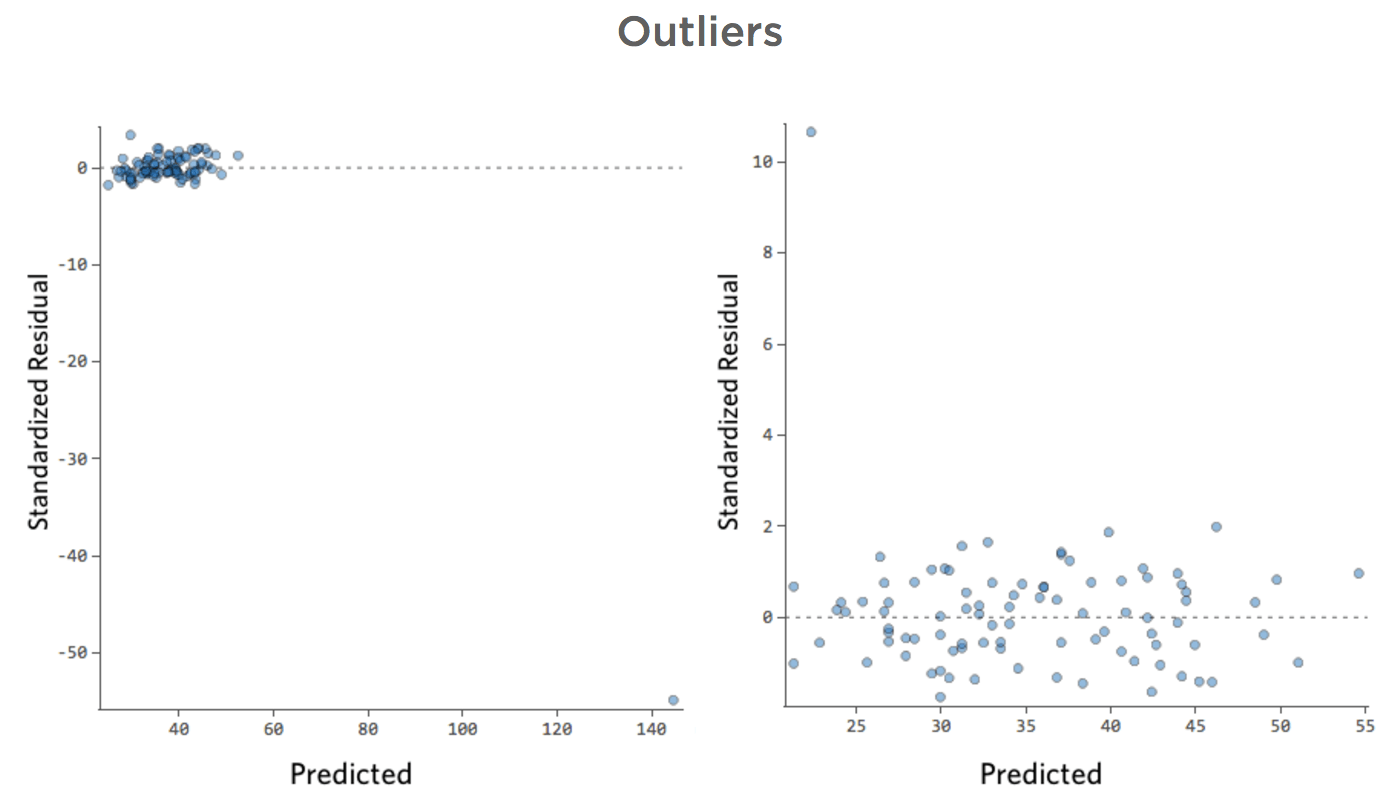
Valores atípicos
- Muestra detalles sobre este diagrama y cómo solucionarlo.
-
Problema
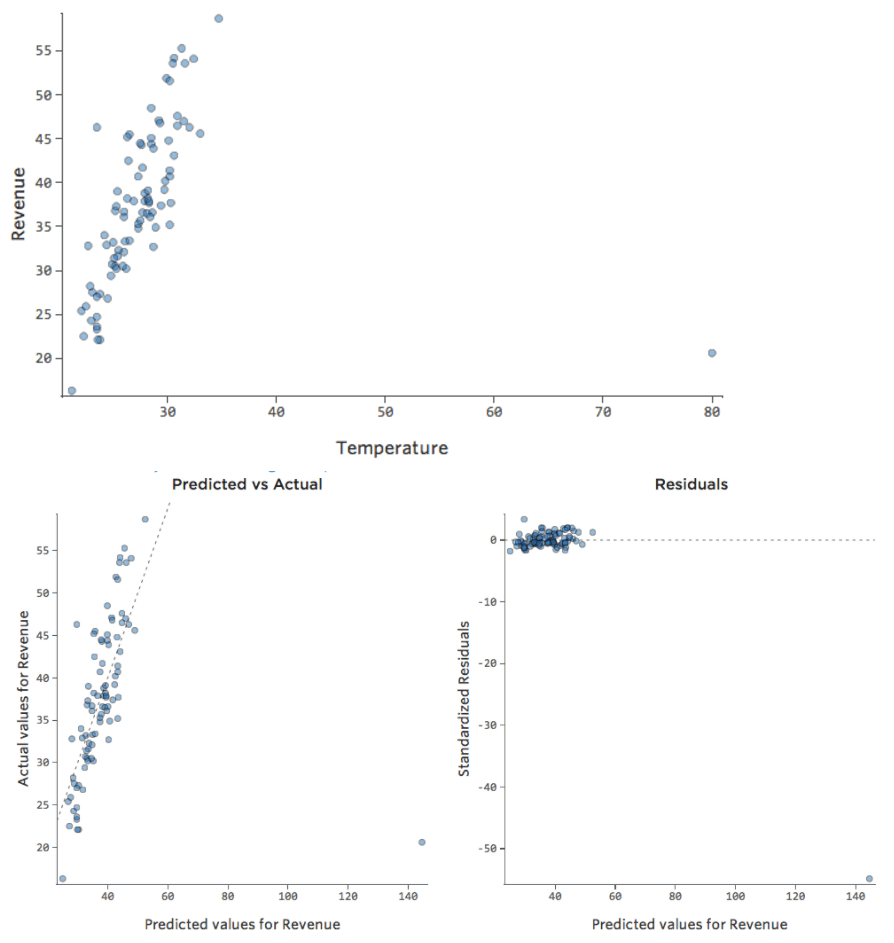
¿Y si uno de sus datos tuviera una “Temperatura” de 80 en lugar de los 20 y 30 normales? Sus diagramas se verían así:
Esta regresión tiene un dato atípico en una variable de entrada, “Temperatura” (los valores atípicos en una variable de entrada también se conocen como “puntos de apalancamiento”).
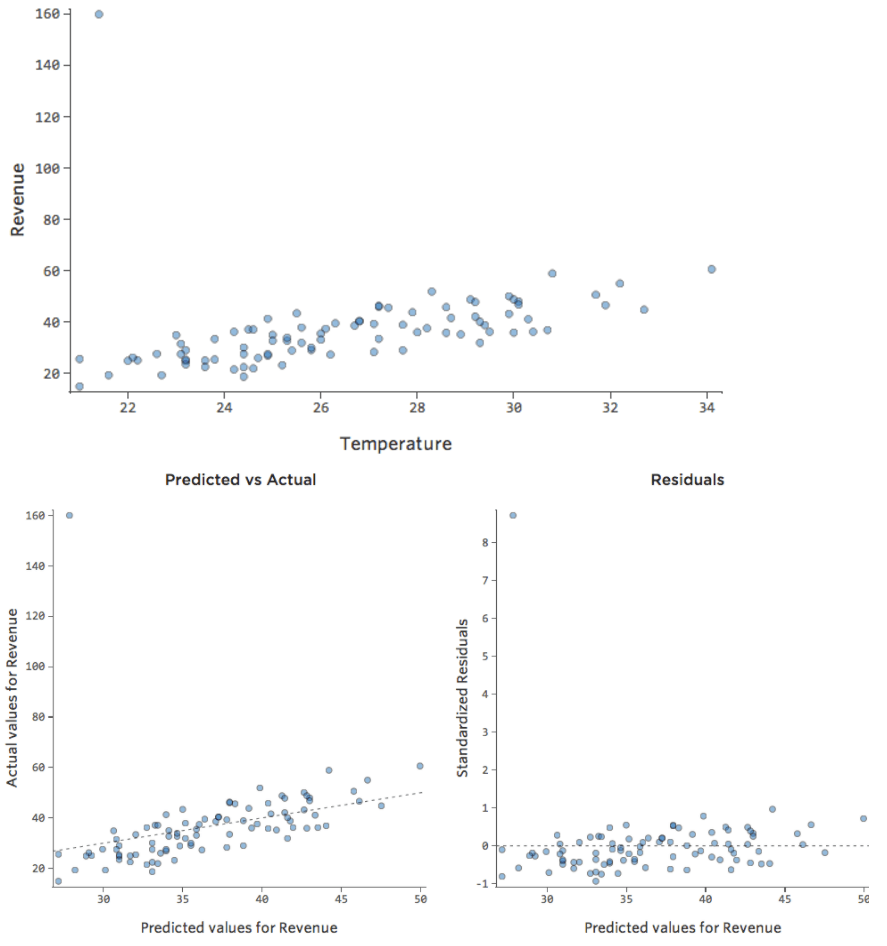
¿Y si uno de sus datos tuviera $160 en ingresos en lugar de los $20 – $60 normales? Sus diagramas se verían así:
Esta regresión tiene un dato atípico en una variable de salida, “Ingresos”.
Implicaciones
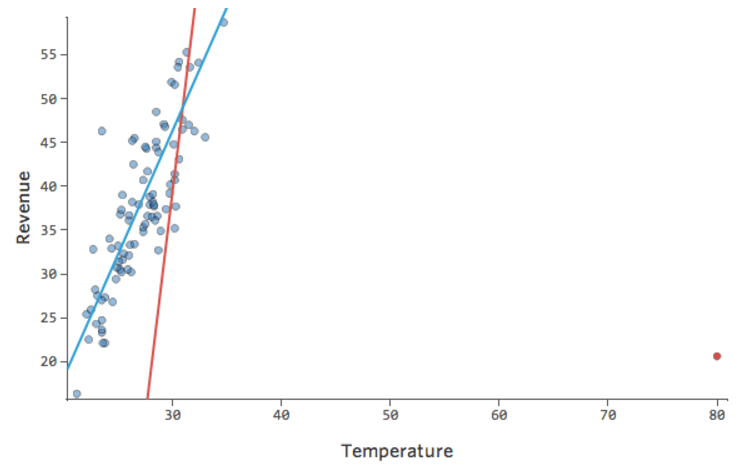
Stats iQ ejecuta un tipo de regresión que generalmente no se ve afectado por los valores atípicos de salida (como el día con ingresos de $160), pero se ve afectado por los valores atípicos de entrada (como una “Temperatura” de 80). En el peor de los casos, su modelo puede girar para intentar acercarse a ese punto a expensas de estar cerca de todos los demás y terminar siendo completamente incorrecto, como este:
La línea azul es probablemente como desea que se vea su modelo, y la línea roja puede ser el modelo que resulte si tiene ese valor atípico en “Temperatura” 80.
Cómo arreglarlo
- Es posible que se trate de un error de medición o de entrada de datos, en el que el valor atípico sea incorrecto, en ese caso debería borrarlo.
- Es posible que lo que parece ser solo un par de valores atípicos sea en realidad una distribución de capacidad. Considere transformar la variable si una de las suyas tiene una distribución asimétrica (es decir, no tiene una remota forma de campana).
- Si se trata de un valor atípico legítimo, debe evaluar el impacto de dicho valor.
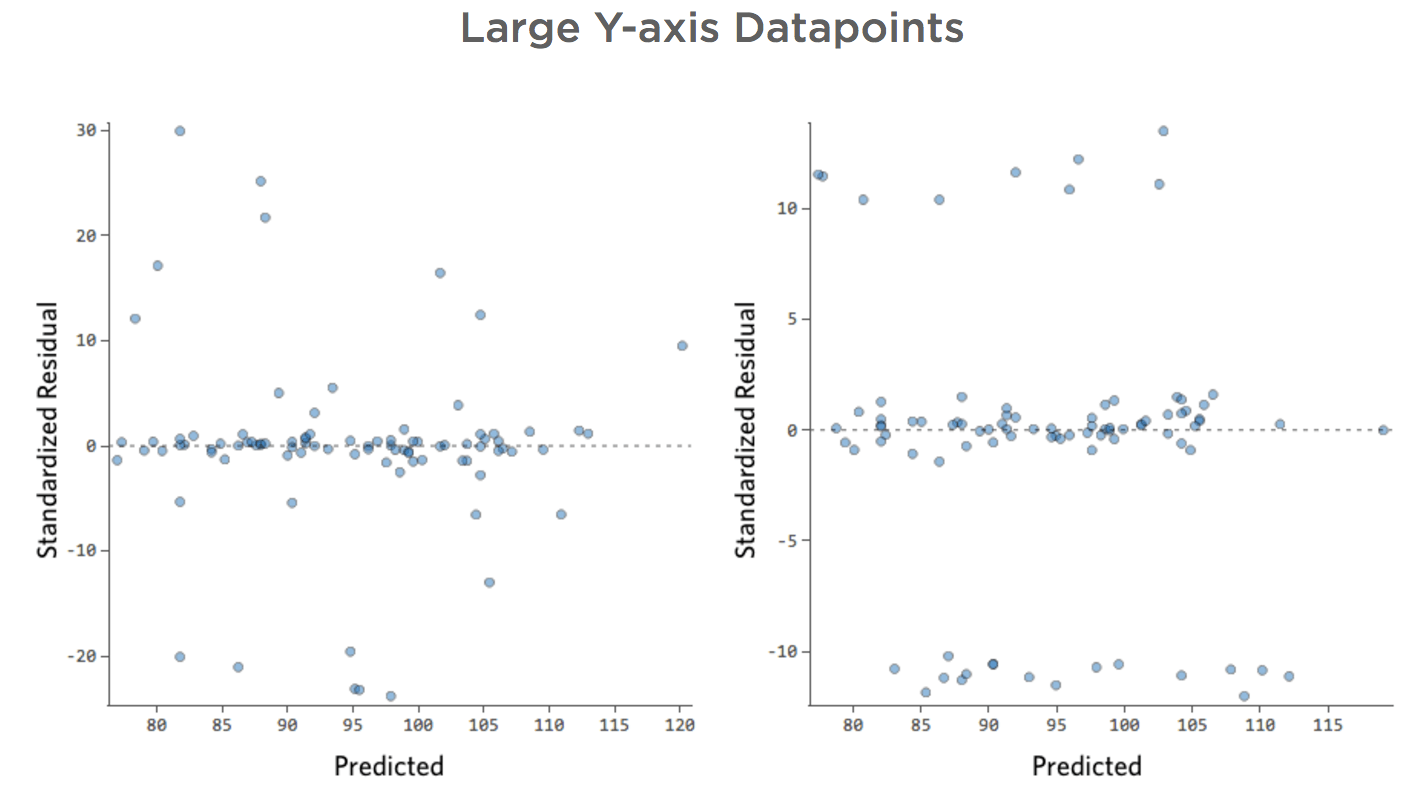
Grandes datos en el eje Y
- Muestra detalles sobre este diagrama y cómo solucionarlo.
-
Problema
Imagine que hay dos puestos de limonada de la competencia cerca. La mayoría de las veces solo uno es operativo, en cuyo caso sus ingresos son consistentemente buenos. A veces ninguno de los dos está activo y los ingresos se disparan; en otras ocasiones, ambos son activos y los ingresos van en picada.
“Ingresos” vs. “Temperatura” podría verse así…
…con la fila superior que son los días cuando no abre ninguno de los competidores y la fila inferior son los días en los que están abiertos.
Esto daría como resultado estos diagramas residuales:
Es decir, hay bastantes datos en ambos lados de 0 que tienen residuales de 10 o más, es decir, que el modelo estaba muy alejado.
Si hubiera recopilado datos todos los días para una variable llamada “Número de puestos de limonada activos”, podría añadir esa variable a su modelo y este problema se solucionaría. Pero a menudo no tiene los datos que necesita (o incluso una estimación de qué tipo de variable necesita).
Implicaciones
Su modelo no es del todo inútil, pero definitivamente no es tan bueno como si tuviera todas las variables que necesitaba. Podría seguir usándolo y podría decir algo así como: “Este modelo es bastante preciso la mayor parte del tiempo, pero de vez en cuando es muy lejano”. ¿Eso es útil? Probablemente, pero esa es su decisión y depende de qué decisiones intente tomar en función de su modelo.
Cómo arreglarlo
- Aunque este enfoque no funcione en el ejemplo específico anterior, casi siempre vale la pena mirar a su alrededor para ver si existe la oportunidad de transformar una variable de manera útil.
- Sin embargo, si eso no funciona, es probable que deba lidiar con el problema de la variable que falta.
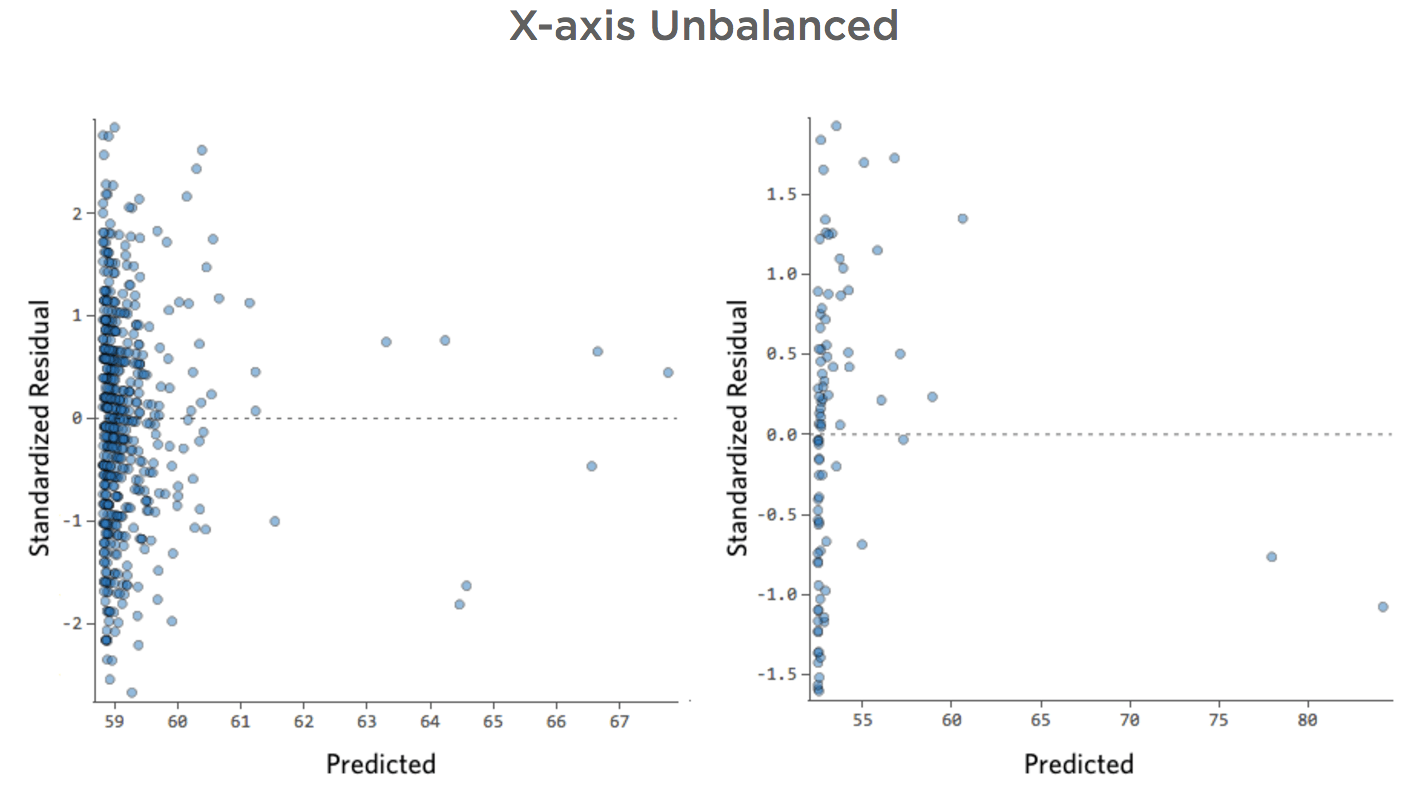
Eje X desequilibrado
- Muestra detalles sobre este diagrama y cómo solucionarlo.
-
Problema
Imagine que “Ingresos” es impulsado por el cercano “Tráfico peatonal”, además de o en lugar de solo “Temperatura”. Imagine que, por la razón que sea, su puesto de limonada suele tener bajos ingresos, pero de vez en cuando obtiene unos días de ingresos extremadamente altos de tal manera que sus ingresos se ven así…
Así que “Tráfico peatonal” vs. “Ingresos” puede tener este aspecto, con la mayoría de los datos agrupados en el lado izquierdo:
La línea negra representa la ecuación del modelo, la predicción del modelo de la relación entre “Tráfico peatonal” e “Ingresos”. Puede ver que el modelo realmente no logra distinguir la diferencia entre “Tráfico peatonal” de 0 y de, por ejemplo, 100 o 1000; para cada uno de esos valores predeciría ingresos cerca de $53.
Traducir los mismos datos a los diagramas de diagnóstico:
Implicaciones
A veces no hay nada malo en su modelo. En el ejemplo anterior, está bastante claro que este no es un buen modelo, pero a veces el diagrama residual está desequilibrado y el modelo es bastante bueno.
Las únicas maneras de contar son a) experimentar con la transformación de sus datos y ver si puede mejorarlos y b) observar el diagrama de Previsto vs. Efectivo y ver si su predicción está extremadante alejada por muchos puntos, como en el ejemplo anterior (pero a diferencia del siguiente ejemplo).
Si bien no hay ninguna regla explícita que diga que el residual no puede estar desequilibrado y seguir siendo preciso (de hecho, este modelo es bastante preciso), a menudo ocurre que un residual desequilibrado en el eje X significa que el modelo se puede hacer mucho más preciso. La mayoría de las veces verá que el modelo era direccionalmente correcto, pero bastante impreciso en relación con una versión mejorada. No es raro solucionar un problema como este y, en consecuencia, ver el salto del cuadrado R del modelo de 0,2 a 0,5 (en una escala de 0 a 1).
Cómo arreglarlo
- La solución a esto es casi siempre transformar sus datos, por lo general en una variable explicativa. (Tenga en cuenta que en el ejemplo que se muestra a continuación, se hace referencia a la transformación de la variable de respuesta, pero el mismo proceso será útil aquí).
- También es posible que su modelo carezca de una variable.
Mejorar su modelo: evaluar el impacto de un valor atípico
Supongamos que tiene un dato atípico que es legítimo, no un error de medición o de datos. Para decidir cómo avanzar, debe evaluar el impacto de los datos en la regresión.
La forma más fácil de hacerlo es anotar los coeficientes de su modelo actual y, luego, filtrar ese punto de datos de la regresión. Si el modelo no cambia un gran que, no tiene mucho de qué preocuparse.
Si eso cambia el modelo de forma significativa, examínelo (en particular el Efectivo vs. el Previsto) y decida cuál es el más adecuado para su caso. Está bien descartar en última instancia el valor atípico siempre y cuando teóricamente pueda defender eso, diciendo: “En este caso no estamos interesados en los valores atípicos, simplemente no son de interés” o “Ese fue el día en que el tío Jerry vino a comprarme y me dio una propina de $100; eso no es predecible, y no vale la pena incluirlo en el modelo”.
Mejorar su modelo: transformar variables
Visión general
La forma más común de mejorar un modelo es transformar una o más variables, normalmente utilizando una transformación de los registros o “log”.
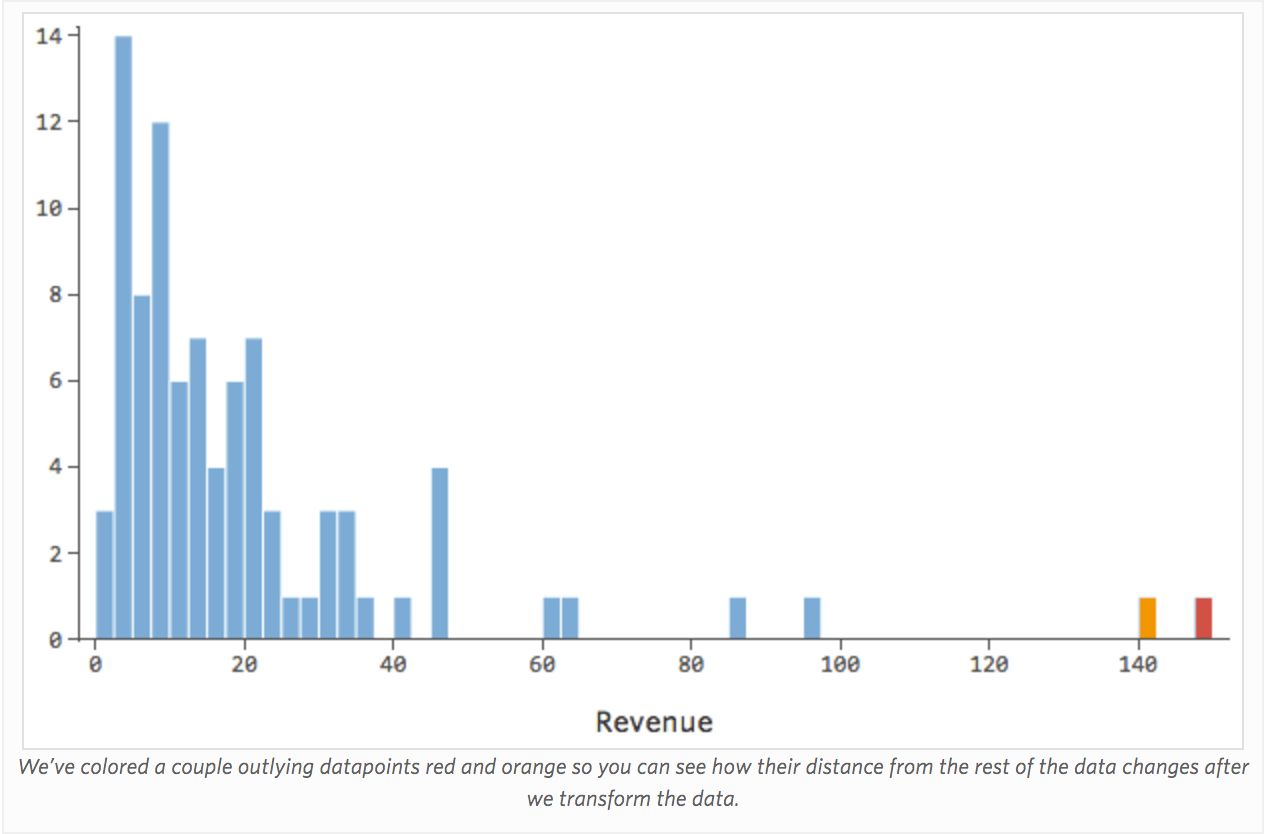
La transformación de una variable cambia la forma de su distribución. Típicamente el mejor lugar para comenzar es una variable que tiene una distribución asimétrica, a diferencia de una distribución más simétrica o en forma de campana. Encuentre una variable como esta para transformarse:
En general, los modelos de regresión funcionan mejor con curvas más simétricas en forma de campana. Pruebe con diferentes tipos de transformaciones hasta llegar a la más cercana a esa forma. A menudo no es posible acercarse a eso, pero ese es el objetivo. Supongamos que toma la raíz cuadrada de “Ingresos” como un intento de llegar a una forma más simétrica, y su distribución tiene este aspecto:
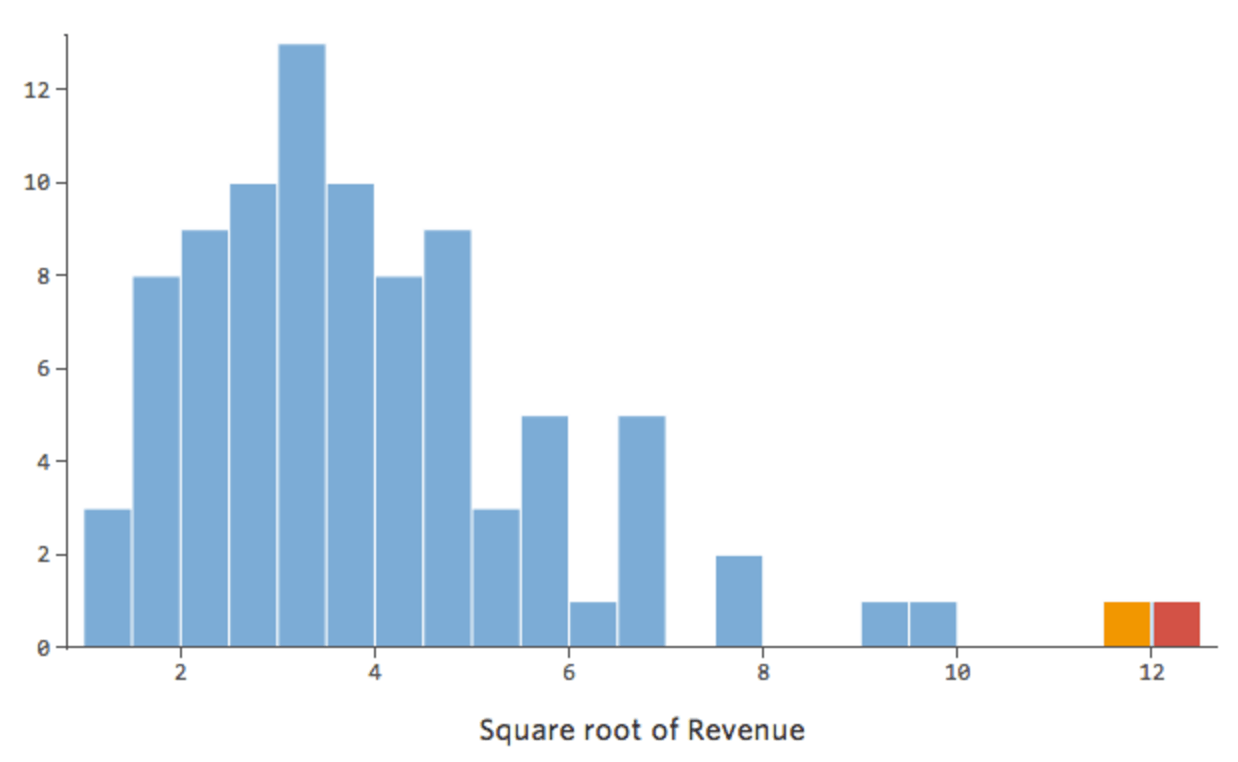
Eso está bien, pero sigue siendo un poco asimétrico. En su lugar, intentemos tomar el registro de “Ingresos”, que produce esta forma:
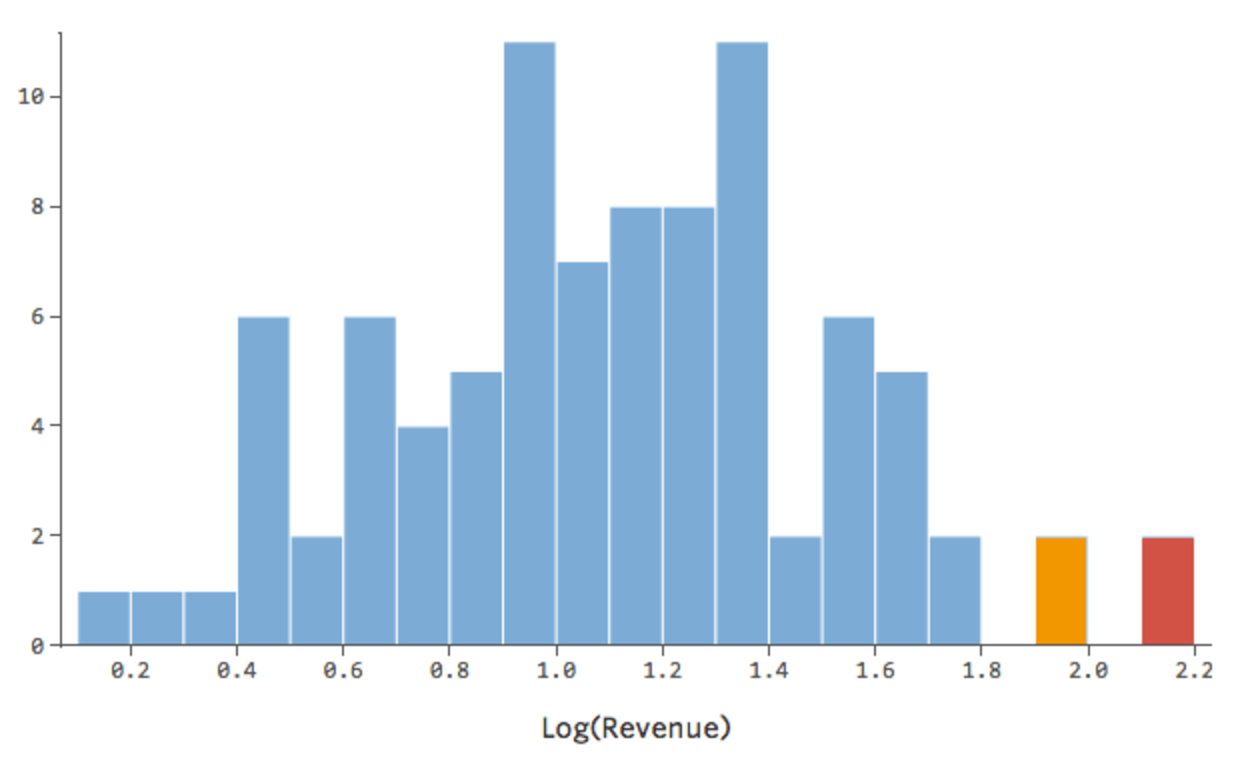
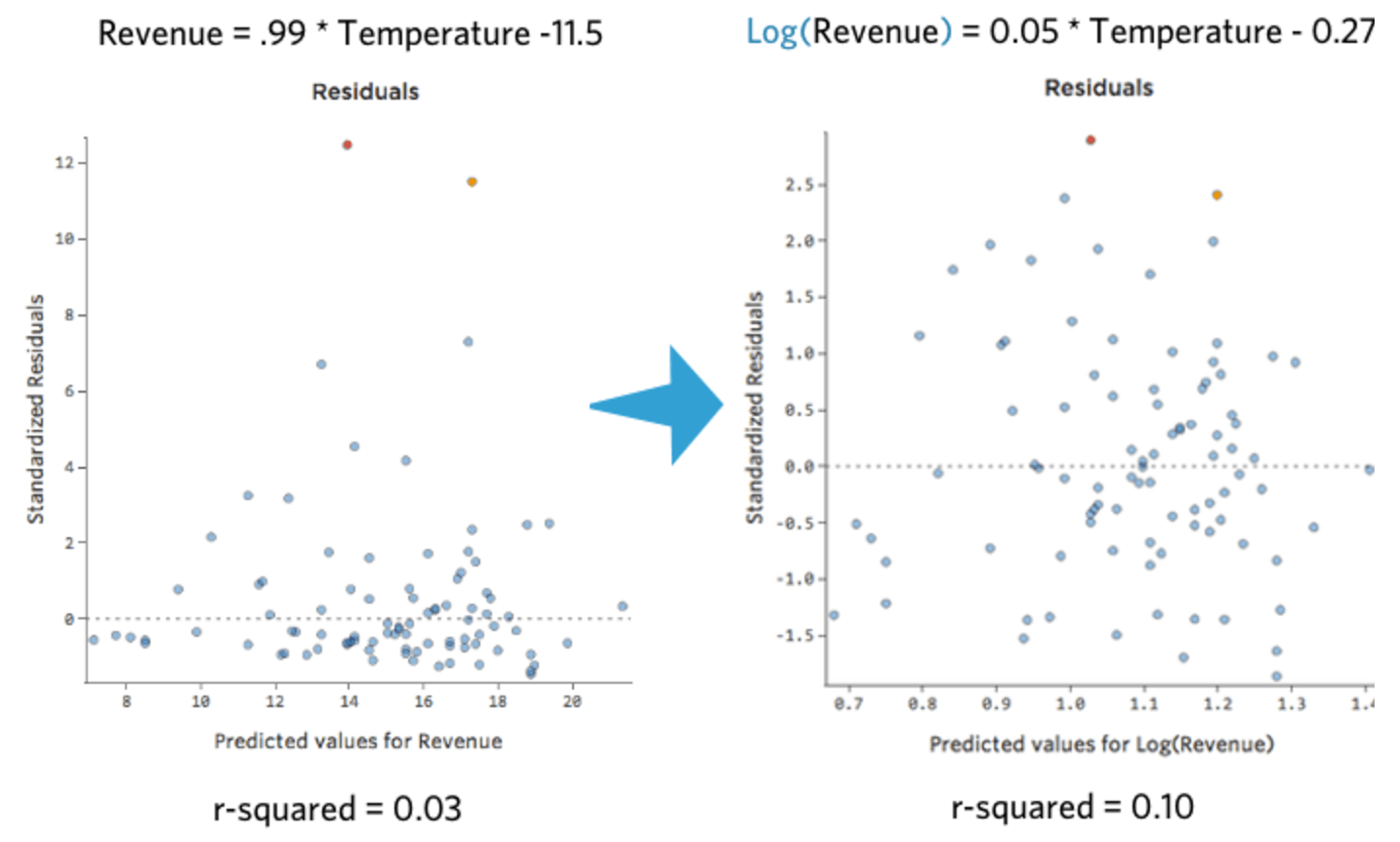
Eso es bonito y simétrico. Probablemente obtendrá un mejor modelo de regresión con log(“Ingresos”) en lugar de “Ingresos”. De hecho, esta es la forma en que su ecuación, sus residuales y su cuadrado R pueden cambiar:
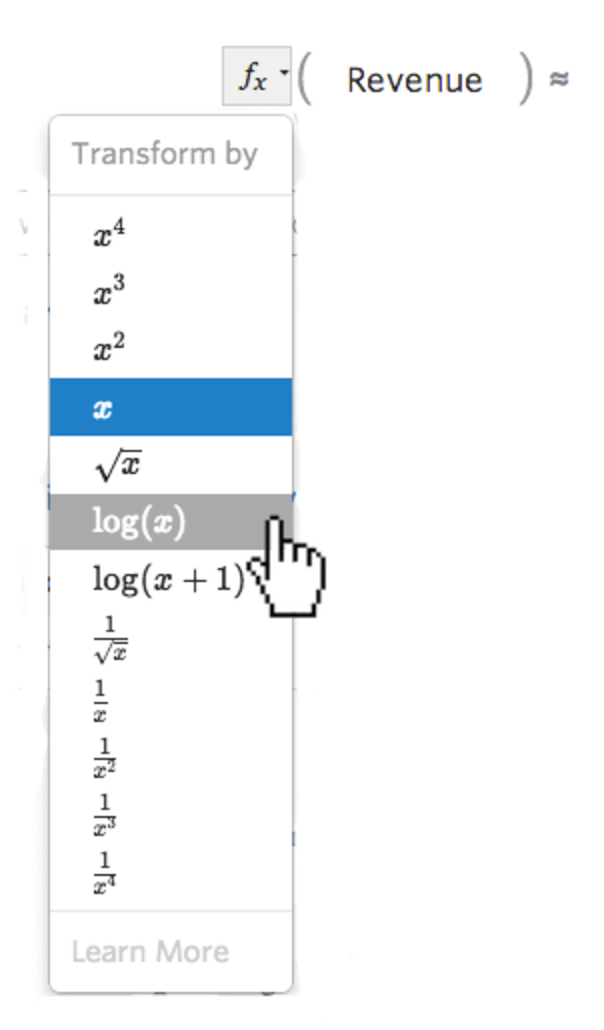
Stats iQ muestra una versión pequeña de la distribución de la variable en línea con la ecuación de regresión: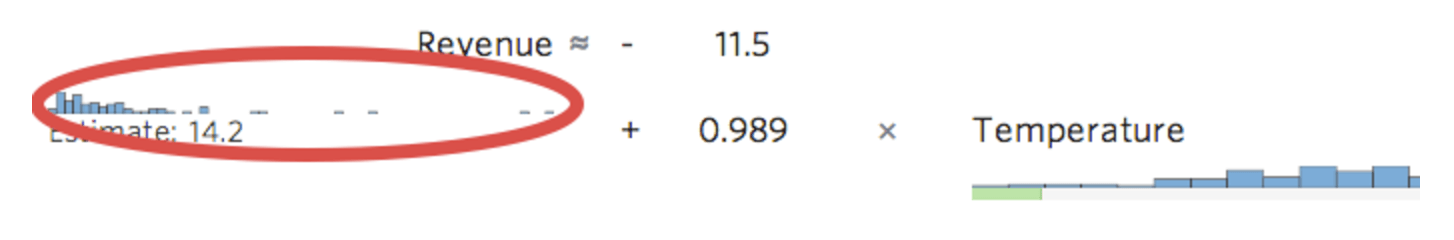
Seleccione el botón fx de transformación a la izquierda de la variable…
…luego seleccione una transformación, la mayoría de las veces log(x)…
…luego examine el histograma para ver si está más centrado, ya que este es después de la transformación:

Después de transformar una variable, tenga en cuenta cómo cambian su distribución, el cuadrado R de la regresión y los patrones residuales del diagrama. Si mejoran (en particular, el cuadrado R y el residual), probablemente sea mejor mantener la transformación.
Si es necesario realizar una transformación, inicie por una transformación de “log” porque los resultados de su modelo seguirán siendo fáciles de entender. Tenga en cuenta que se producirán problemas si los datos que está intentando transformar incluyen ceros o valores negativos. Para saber por qué es tan útil tomar un log, o si tiene números no positivos que desea transformar, o si solo desea comprender mejor lo que sucede cuando transforma datos, lea los detalles a continuación.
Detalles
Si toma el log10() de un número, está diciendo “10 que elevado a la n potencia me da ese número”. Por ejemplo, esta es una tabla simple con cuatro datos, incluidos “Ingresos” y Log(“Ingresos”):
| Temperatura | Ingresos | Log(Ingresos) |
|---|---|---|
| 20 | 100 | 2 |
| 30 | 1000 | 3 |
| 40 | 10 000 | 4 |
| 45 | 31 623 | 4,5 |
Tenga en cuenta que si trazamos “Temperatura” vs. “Ingresos” y “Temperatura” vs. Log(“Ingresos”), el último modelo se ajusta mucho mejor.
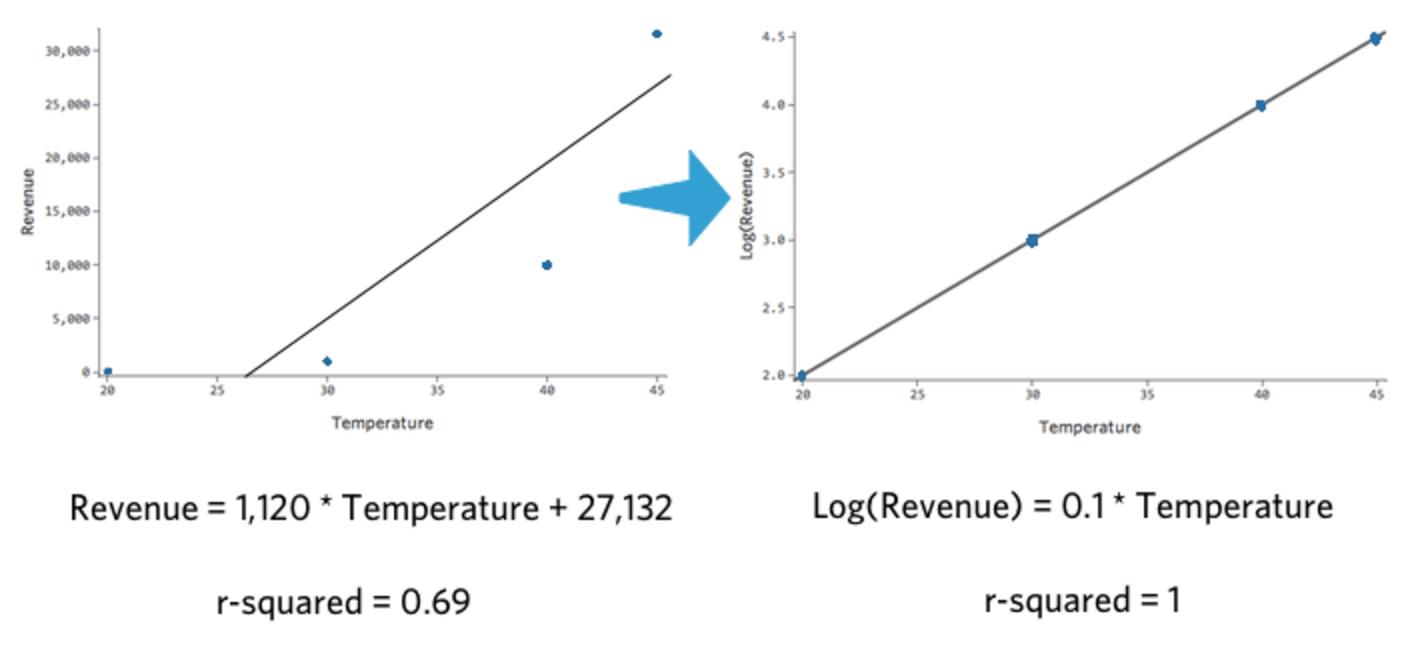
Lo interesante de esta transformación es que su regresión ya no es lineal. Cuando “Temperatura” pasó de 20 a 30, “Ingresos” pasó de 10 a 100, una brecha de 90 unidades. Luego cuando “Temperatura” pasó de 30 a 40, “Ingresos” pasó de 100 a 1000, una brecha mucho mayor.
Si ha tomado un log de la variable de respuesta, ya no se da el caso de que un aumento de una unidad en “Temperatura” signifique un aumento de la unidad X en “Ingresos”. Ahora es un aumento X–por ciento en “Ingresos”. En este caso, un aumento de diez unidades en “Temperatura” se asocia con un aumento del 1000 % en Y, es decir, un aumento de una unidad en “Temperatura” se asocia con un aumento del 26 % en “Ingresos”.
Tenga en cuenta también que no puede tomar el log de 0 o un número negativo (no hay X donde 10X = 0 o 10X= -5), por lo que si realiza una transformación de log, perderá esos puntos de datos de la regresión. Existen 4 formas comunes de gestionar la situación:
- Tomar una raíz cuadrada o una raíz cúbica. Esos no cambiarán la forma de la curva tan drásticamente como tomar un registro, pero permiten que los ceros permanezcan en la regresión.
- Si no son demasiadas filas de datos las que tienen cero y esas filas no son teóricamente importantes, puede decidir continuar con el log y perder algunas filas de la regresión.
- En lugar de tomar log(y), tome log(y+1), de modo que los ceros se conviertan en 1 y luego se puedan mantener en la regresión. Esto sesga un poco su modelo y es bastante mal visto, pero en la práctica, sus efectos secundarios negativos son típicamente menores.
Mejorar su modelo: faltan variables
Probablemente la razón más común por la que un modelo no se ajusta es que no se incluyen todas las variables correctas. En este caso particular, hay muchas soluciones posibles.
Añadir una nueva variable
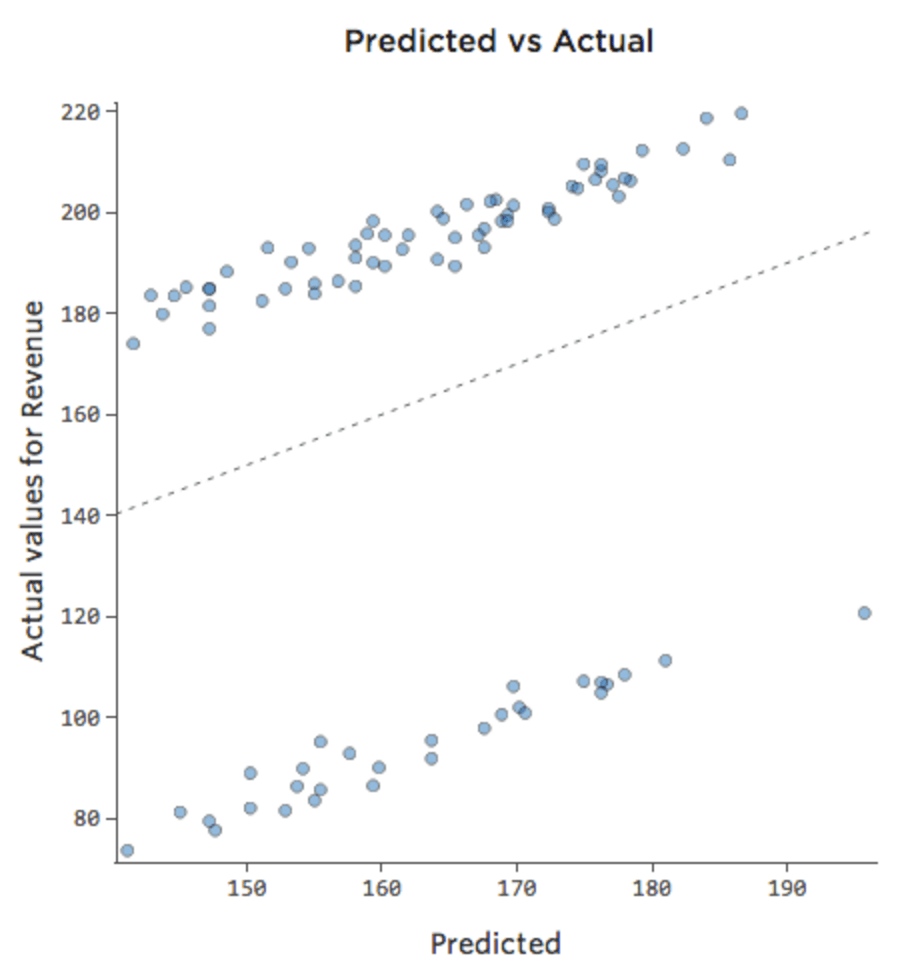
A veces, la corrección es tan fácil como añadir otra variable al modelo. Por ejemplo, si el tráfico de “ingresos” del puesto de limonada fue mayor en los fines de semana que durante la semana, el diagrama de Previsto vs. Efectivo podría ser el siguiente (cuadrado R de 0,053), ya que el modelo solo toma el promedio de los fin de semana y de los días de la semana:
Si el modelo incluye una variable llamada “Fin de semana”, entonces el gráfico Previsto vs. Efectivo podría verse así (cuadrado R de 0,974):
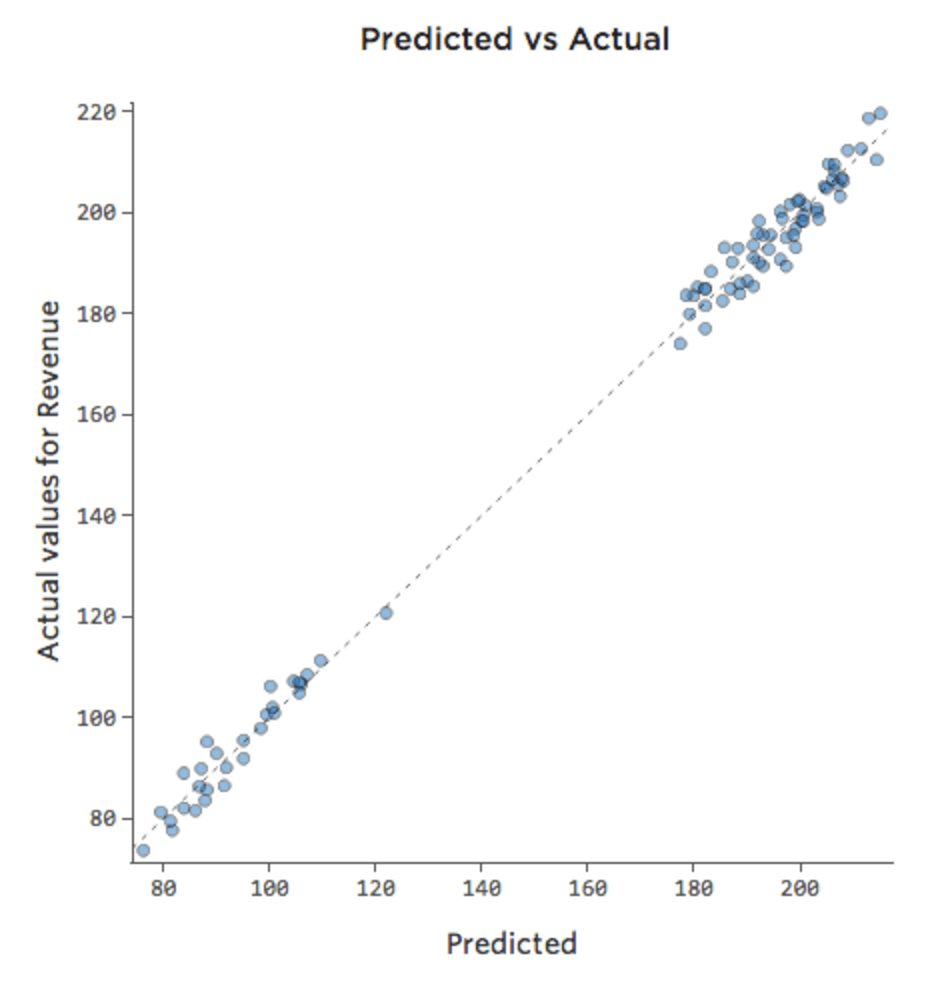
El modelo realiza predicciones mucho más precisas porque puede considerar si un día de la semana es un día de la semana o no.
Tenga en cuenta que a veces necesitará crear variables en Stats iQ para mejorar su modelo de esta manera. Por ejemplo, es posible que tenga una variable “Fecha” (con valores como “26/10/2014”) y tenga que crear una nueva variable llamada “Día de la semana” (es decir, domingo) o Fin de semana (es decir, fin de semana).
Variable omitida no disponible
Sin embargo, pocas veces es tan fácil. Muy a menudo, la variable relevante no está disponible porque no sabe lo que es o era difícil de recopilar. Tal vez no fue una cuestión de fin de semana vs. día de la semana, sino algo como “Número de competidores en la zona” que no logró recopilar en ese momento.
Si la variable que necesita no está disponible, o ni siquiera sabe lo que sería, su modelo no se puede mejorar realmente y debe evaluarlo y decidir qué tan feliz está con él (si es útil o no, aunque sea defectuoso).
Interacciones entre variables
Tal vez los fines de semana el puesto de limonada siempre vende al 100 % de su capacidad, por lo que independientemente de la “Temperatura”, los “Ingresos” son altos. Pero los días de semana, el puesto de limonada está mucho menos ocupado, por lo que la “Temperatura” es un importante impulsor de los “Ingresos”. Si ejecuta una regresión que incluye “Fin de semana” y “Temperatura”, es posible que vea un diagrama Previsto vs. Efectivo como este, donde la fila a lo largo de la parte superior son los días de fin de semana.
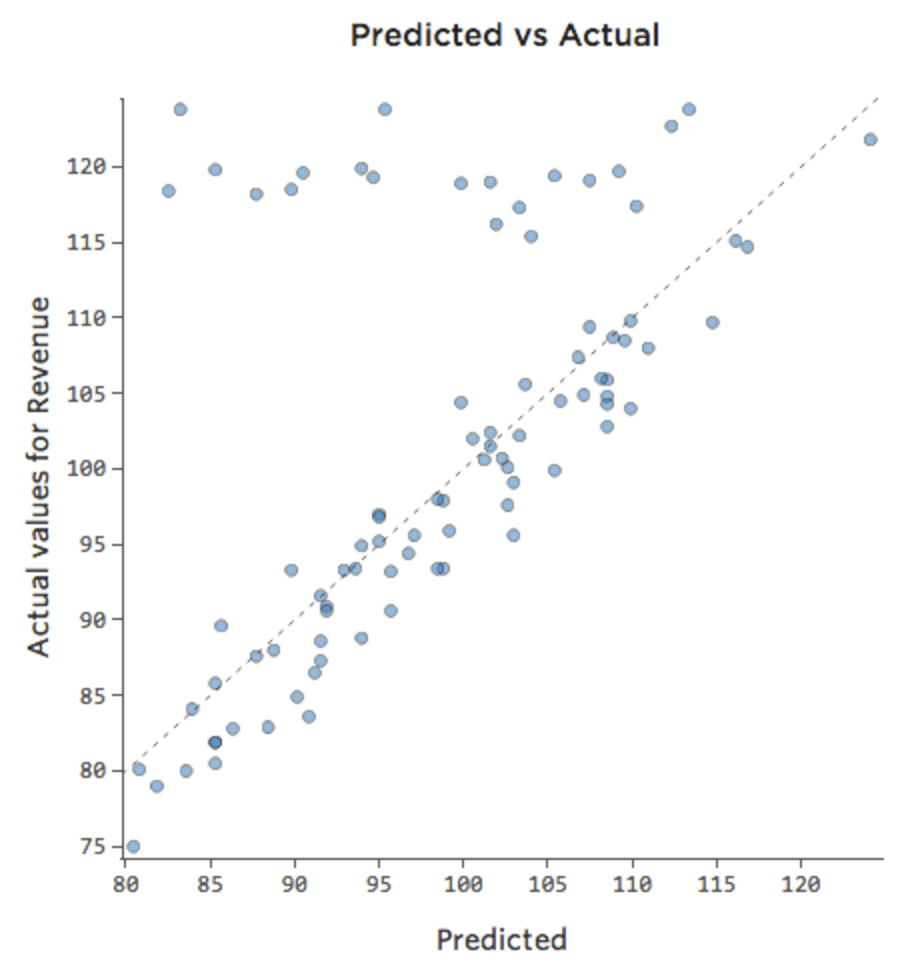
Diríamos que hay una interacción entre “Fin de semana” y “Temperatura”: el efecto de uno de ellos en “Ingresos” es diferente en función del valor del otro. Si creamos una variable de interacción, obtenemos un modelo mucho mejor en el Previsto vs. Efectivo se ve así:
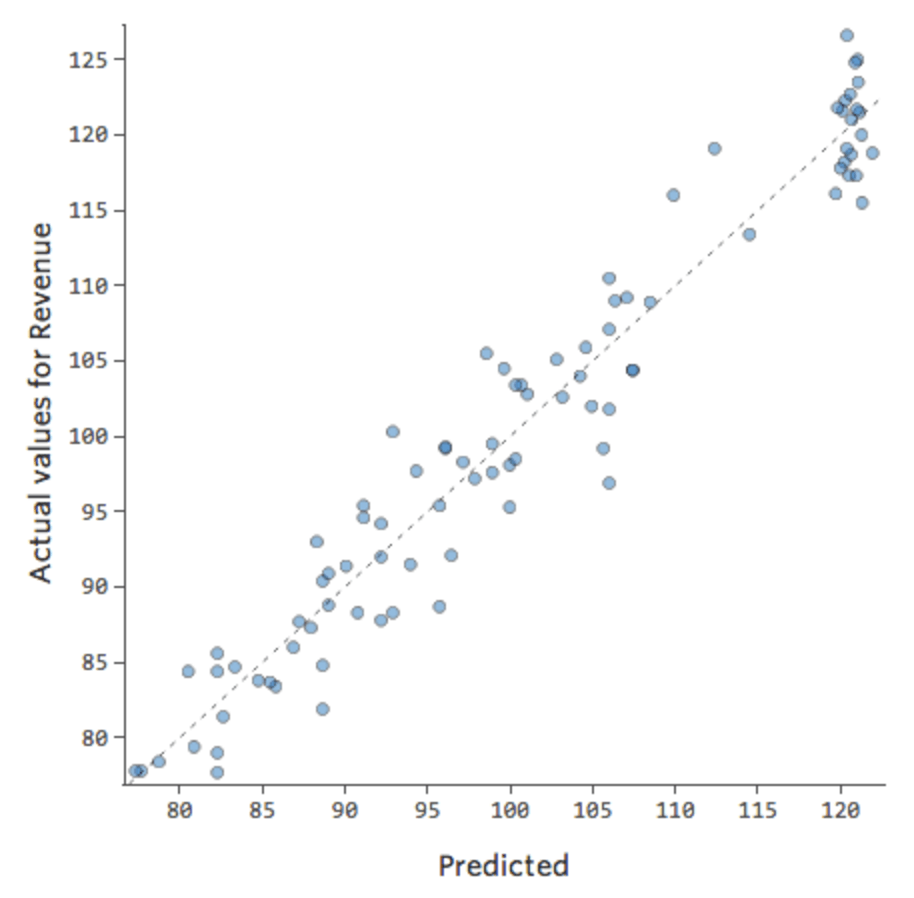
Mejorar su modelo: fijar la no linealidad
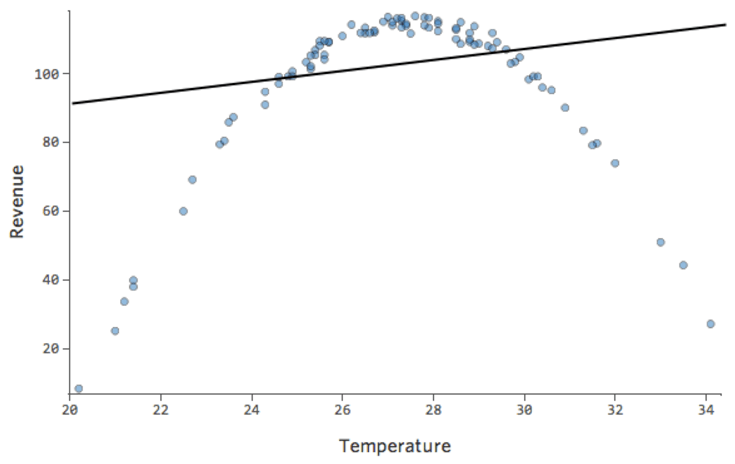
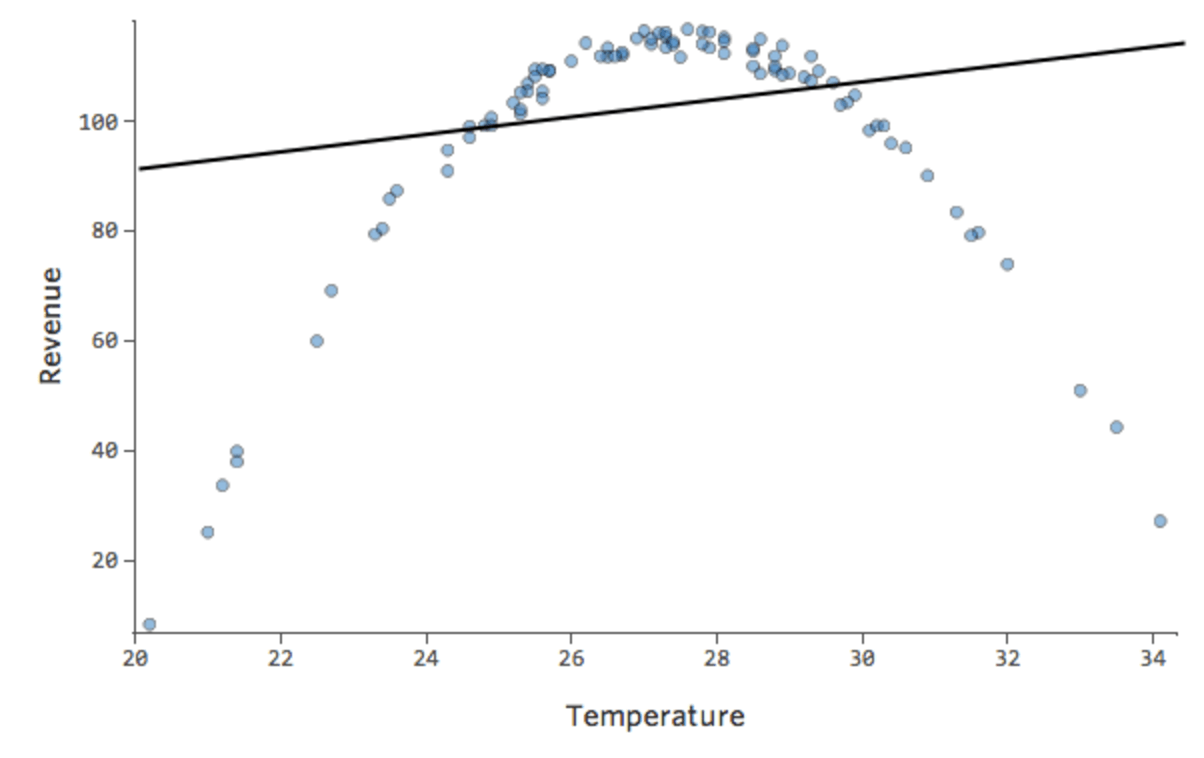
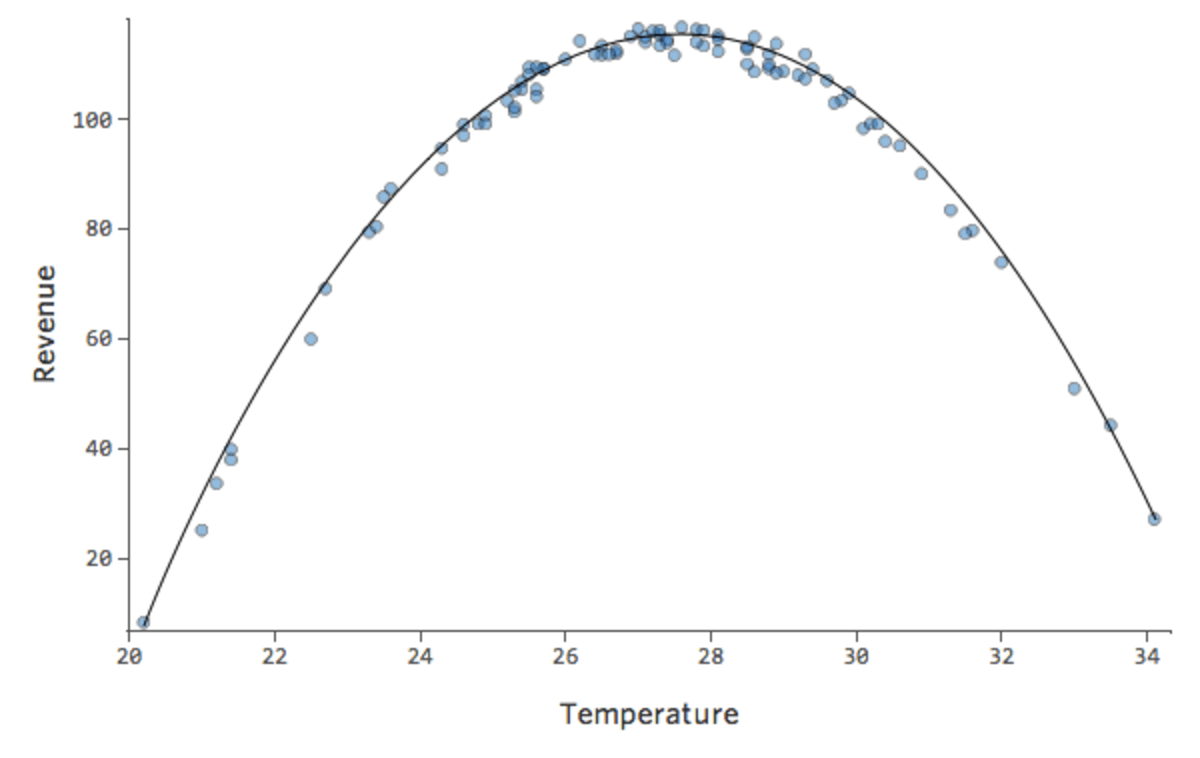
Supongamos que tiene una relación que tiene este aspecto:
Puede notar que la forma es la de una parábola, que por lo general se asocia con este tipo de fórmulas:
y= x2 + x + 1
De forma predeterminada, la regresión utiliza un modelo lineal que tiene este aspecto:
y= x + 1
De hecho, la línea del diagrama anterior tiene esta fórmula:
y= 1,7x + 51
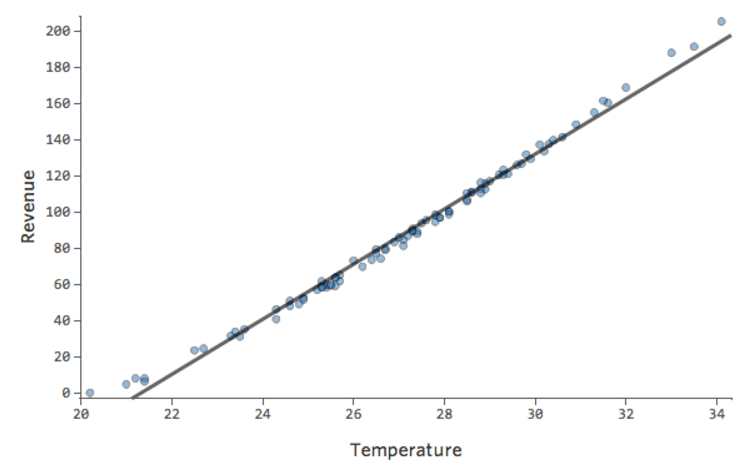
Pero el encaje es terrible. Por lo tanto, si añadimos un término x2, nuestro modelo tiene una mayor probabilidad de encajar la curva. De hecho, crea lo siguiente:
La fórmula para esa curva es:
y= -2x2 +111x – 1408
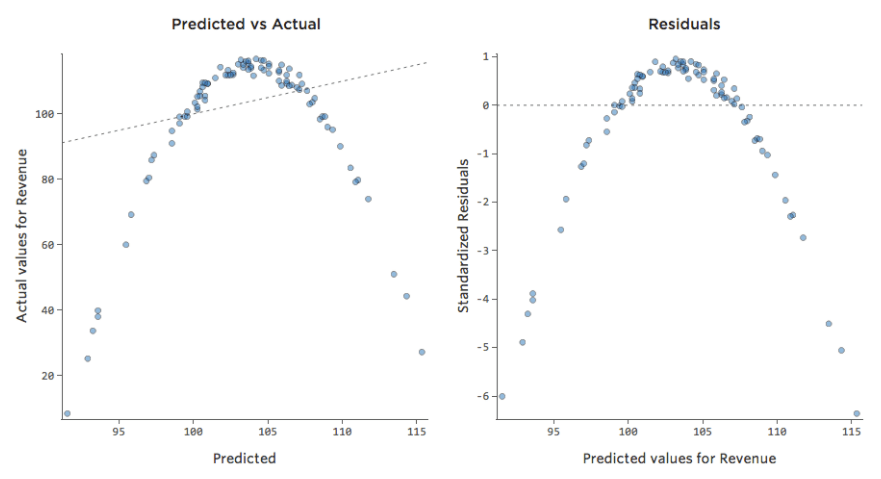
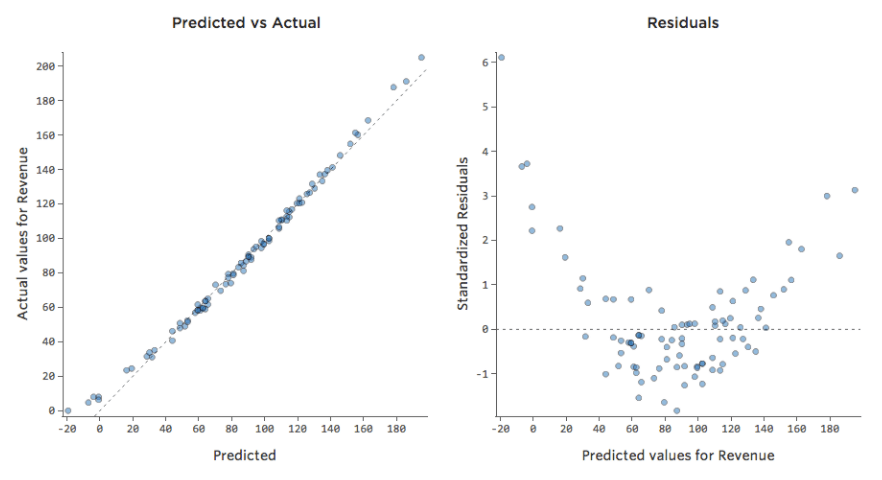
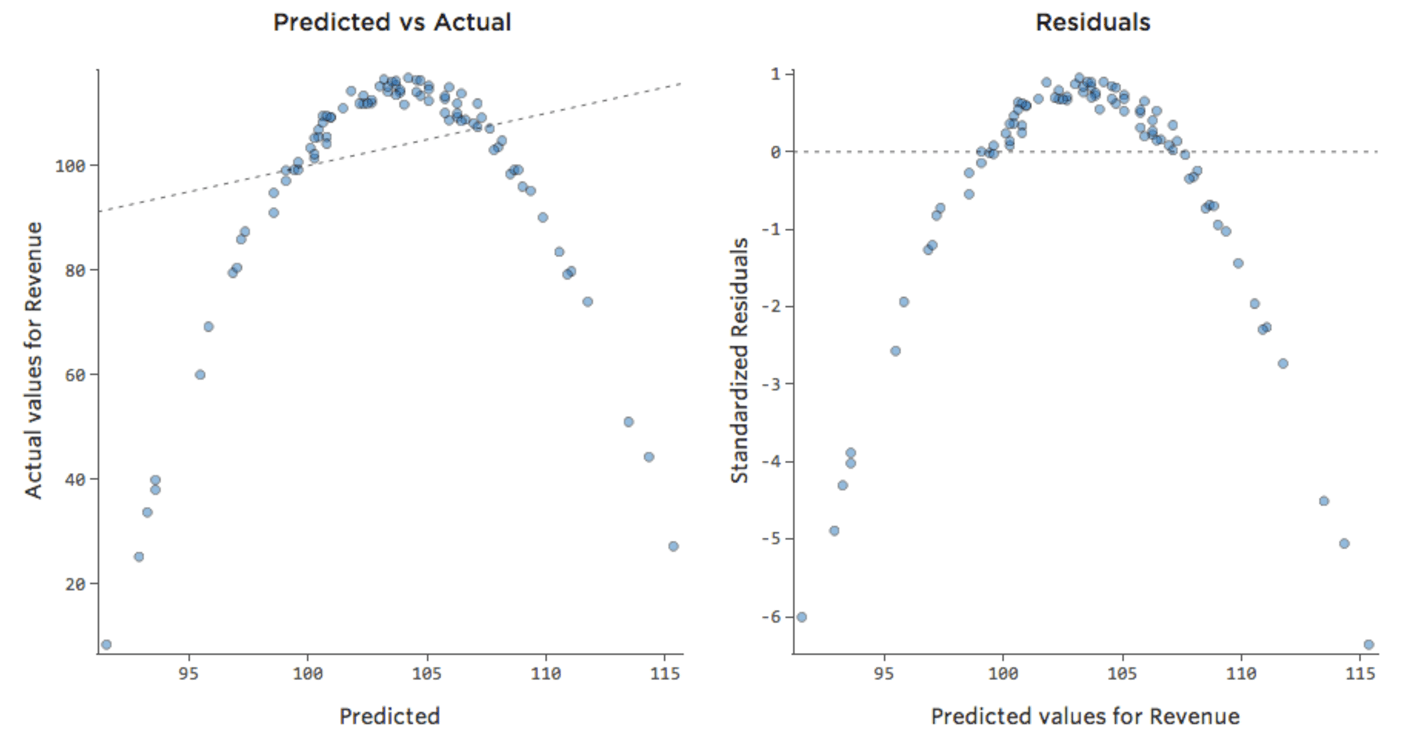
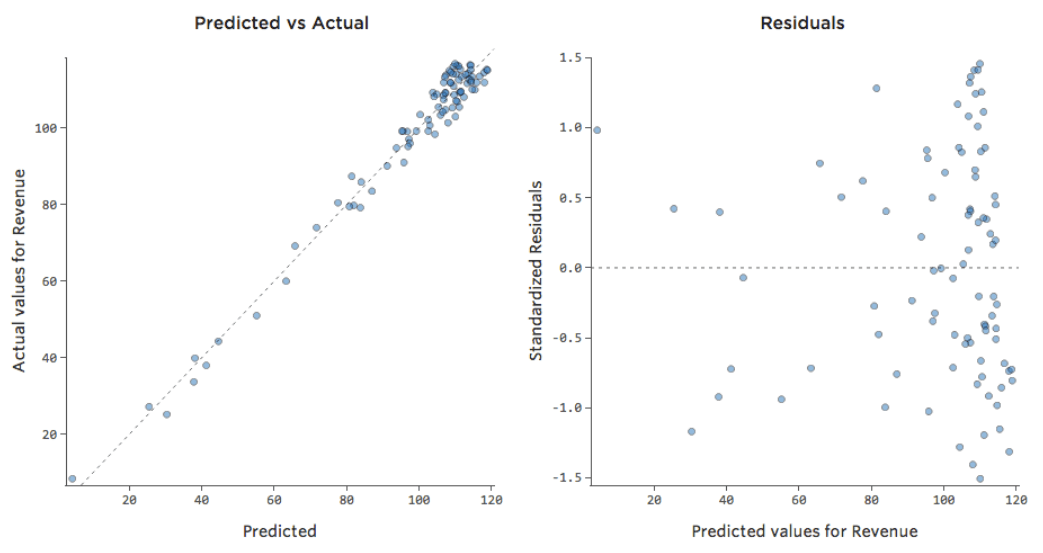
Esto significa que nuestros diagramas de diagnóstico cambian con respecto a esto…
…a esto:
Tenga en cuenta que se trata de diagramas de diagnóstico saludables, aunque los datos parezcan desequilibrados a la derecha de los mismos.
El enfoque anterior se puede extender a otros tipos de formas, particularmente una curva en forma de S, añadiendo el término x3. Sin embargo, eso es muy poco común.
Algunas advertencias:
- Por lo general, si tiene un término x2 debido a un patrón no lineal en sus datos, desea tener un término x común y corriente en lugar de un x2. A lo mejor considera que su modelo puede funcionar sin él, pero definitivamente debería intentar calcular los dos para empezar.
- La ecuación de regresión puede ser difícil de entender. Para la ecuación lineal al principio de esta sección, para cada unidad adicional de “Temperatura”, “Ingresos” subió 1,7 unidades. Cuando tiene x2 y x en la ecuación, no es fácil decir “Cuando la Temperatura sube un grado, esto es lo que pasa”. A veces, por esa razón, es más fácil utilizar una ecuación lineal, asumiendo que la misma encaja lo suficientemente bien.