Scripts R precompuestos
Acerca de los scripts R precompuestos
R es un lenguaje de programación estadística que se utiliza ampliamente para realizar análisis flexibles y potentes. Al utilizar Codificación R en Stats iQPuede seleccionar entre varios scripts de análisis para que el uso de R sea más fácil y eficiente.
Seleccionar un script para código R
- Seleccione las variables que desea analizar. Ver Selección de variables de marco de datos para código R Para más información.
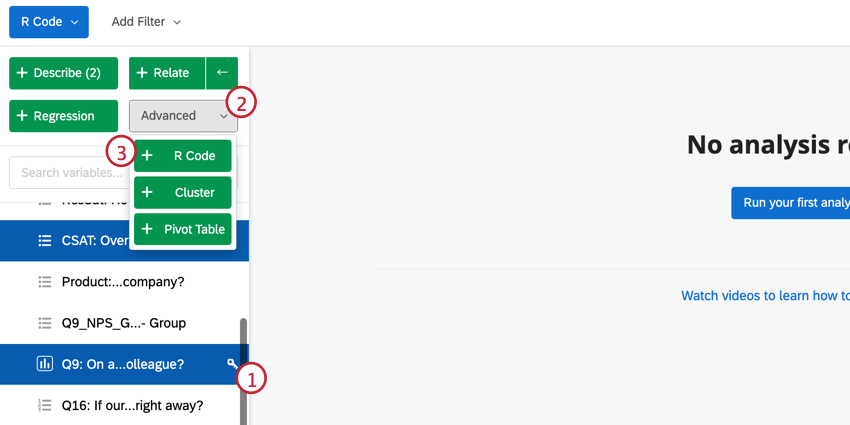
- Hacer clic Avanzado .
- Hacer clic Código R.
- Seleccione un script. Para obtener más información sobre las opciones de análisis, consulte las secciones siguientes.
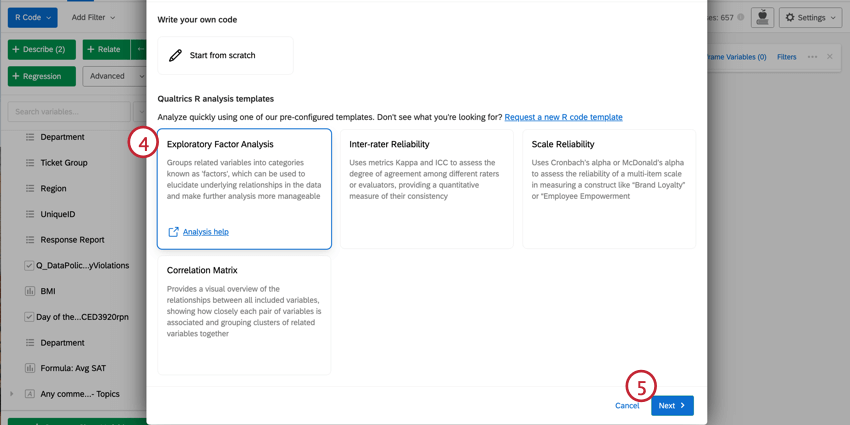
- Haga clic en Siguiente.
- Confirme las variables que ha seleccionado. Si desea cambiar una variable, haga clic en el menú desplegable y seleccione una nueva.
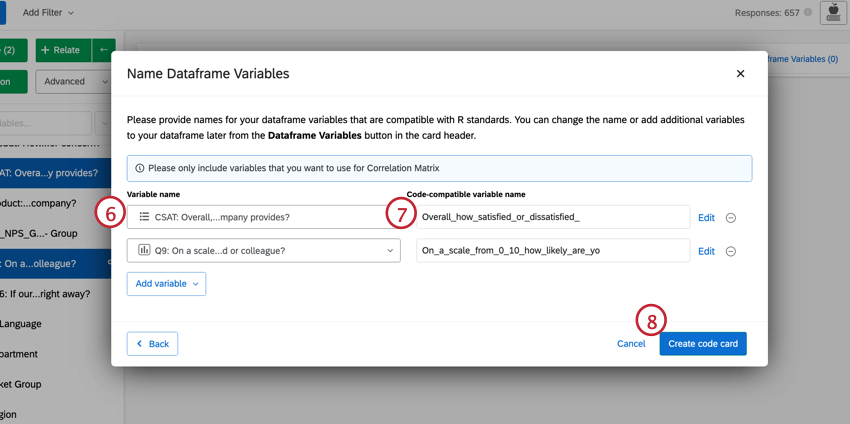
- Edite el nombre de sus variables, si lo desea. Para obtener más información, consulte Nombramiento de variables de marco de datos para código R.
Consejo Q:Puedes realizar cambios en las variables que hayas seleccionado directamente desde esta ventana. Para editar los valores de recodificación, haga clic en Editar. Si desea eliminar la variable, haga clic en el botón ( – ) icono. Si desea agregar una nueva variable, haga clic en Agregar variable En la parte inferior izquierda.
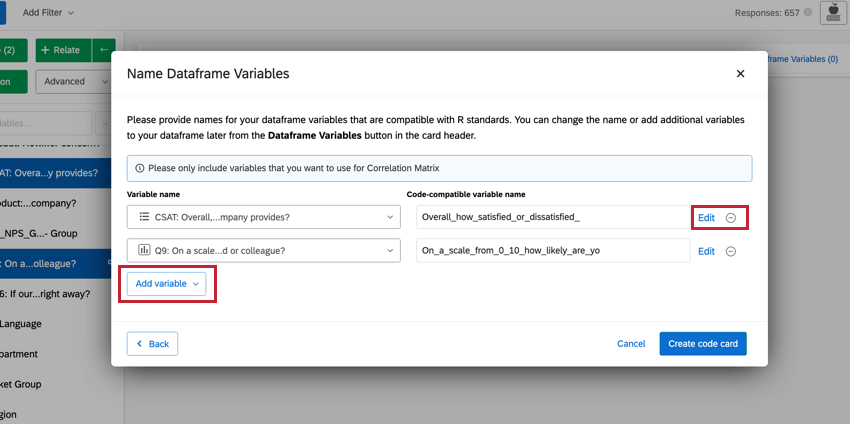
- Cuando haya terminado de editar las variables de su marco de datos, haga clic en Crear tarjeta de código.
Navegación por scripts de código R precompuestos
Su script se pegará en la sección de código de la tarjeta de código R. Este código contendrá consejos junto con los comandos para generar el análisis que ha seleccionado. Para ejecutar su análisis, haga clic en Correr todo. Los resultados se mostrarán en el cuadro de salida de la derecha.
Puede editar las variables de su marco de datos o agregar una filtro al análisis haciendo clic en las opciones de la parte superior derecha. Haga clic en el menú de tres puntos para agregar notas a su tarjeta de código, copiar el análisis o abrir la tarjeta en pantalla completa.
ATAJOS
Se pueden utilizar atajos de teclado para navegar de manera más eficiente por la tarjeta de Código R. Hacer clic Atajos para obtener una lista de posibles acciones.
PAQUETES
La codificación R en Stats iQ viene preinstalada con cientos de los paquetes R más populares utilizados para el análisis. Haga clic en la pestaña Paquetes en la mitad derecha de la tarjeta para ver la lista de paquetes disponibles. Para obtener más información sobre el uso de paquetes, consulte Codificación R en Stats iQ.
Confiabilidad de la escala
La confiabilidad de la escala evalúa hasta qué punto los elementos de una escala de múltiples elementos pueden medir de manera confiable un constructo. En otras palabras, si se mide lo mismo utilizando el mismo conjunto de preguntas, ¿habrá resultados confiablemente similares? Si es así, existe la confianza de que cualquier cambio que veamos en el futuro se deberá a cambios en la población encuestada o a intervenciones que se han realizado para mejorar la puntuación.
INTERPRETACIÓN DE LAS MEDIDAS DE CONFIABILIDAD
Las medidas de confiabilidad de la escala oscilan entre 0 y 1 y son esencialmente una correlación agregada entre todos los elementos de la escala.
El alfa de Cronbach, una medida de confiabilidad ampliamente utilizada, a menudo subestima la confiabilidad debido a ciertas suposiciones. Omega de McDonald’s, una alternativa recomendada, evita estos defectos. Utilizamos el omega de McDonald’s por defecto, pero el alfa de Cronbach todavía es ampliamente aceptado.
No existe una única forma correcta de interpretar el número resultante, pero nuestra regla general preferida para ambos omega se describe a continuación:
| Menos de 0,65 | Inaceptable |
| 0,65 | Aceptable |
| 0,8 | Muy bien |
Si su escala confiable es inaceptable, existen algunas opciones para remediar su conjunto de datos:
- Eliminar cualquier elemento que esté disminuyendo el omega o alfa.
- Es posible que se estén midiendo dos constructos distintos. Si ese es el caso, entonces separar las variables en dos grupos y ejecutar este análisis en cada uno conduciría a puntajes de confiabilidad más altos que los del análisis inicial. Puede explorar esto revisando la matriz de correlación en la salida o utilizando el Análisis factorial exploratorio script para ver qué agrupaciones quedan naturalmente fuera de los datos.
- En última instancia, puede que sea necesario modificar y ejecutar la encuesta nuevamente. Es posible que sea necesario aclarar o reelaborar los elementos que tienen una baja correlación con los demás, o puede ser necesario agregar otros elementos.
resultados muy altos (por ejemplo, 0,95) también pueden indicar un problema con la báscula, normalmente que aún es posible tener una báscula muy fiable sin tener tantos elementos. En este caso, recomendamos eliminar los elementos menos útiles de la escala y volver a ejecutar el análisis.
INTERPRETACIÓN DE ESTADÍSTICAS A NIVEL DE ÍTEM
El script primero ejecuta una medida de confiabilidad general y luego ejecuta una iteración para cada variable. El objetivo del análisis de confiabilidad por ítem es comprender qué ítems son más útiles para la construcción de la escala. Stats iQ generará una tabla similar a esta:
Puntuación general de Omega de McDonald’s: 0,71
| norte | Medio | Correlación artículo-total | Omega de McDonald’s si se elimina | |
| A1 | 2784 | 4.59 | 0.31 | 0.72 |
| A2 | 2773 | 4.80 | 0.56 | 0.69 |
| A3 | 2774 | 4.60 | 0.59 | 0.61 |
| … | … | … | … | … |
- El objetivo general es tener un Omega de McDonald’s más alto con un menor número de artículos. Entonces, si un investigador estuviera creando una nueva escala, probablemente querría eliminar A1, ya que el omega en realidad es más alto sin él.
- El rest de elementos que reducirían la confiabilidad si se eliminaran quedan a criterio del investigador. Por ejemplo, si a un investigador le preocupa la fatiga de la encuesta , podría permitir una disminución mayor en la confiabilidad al decidir eliminar una variable.
- La correlación artículo-total es la correlación entre ese artículo y el promedio de todos los demás. La baja correlación ítem-total sugiere que la variable no es lo suficientemente representativa del constructo subyacente. La regla general más común es sospechar de cualquier cosa que tenga una correlación elemento-total de 0,3 o inferior, especialmente si tiene muchos elementos, lo que infla artificialmente la métrica de confiabilidad.
Si decide eliminar un elemento, deberá volver a ejecutar todas las demás estadísticas antes de decidir si desea eliminar otro elemento. En Stats iQ, esto significa simplemente eliminar la variable de toda la tarjeta: el rest se realizará automáticamente.
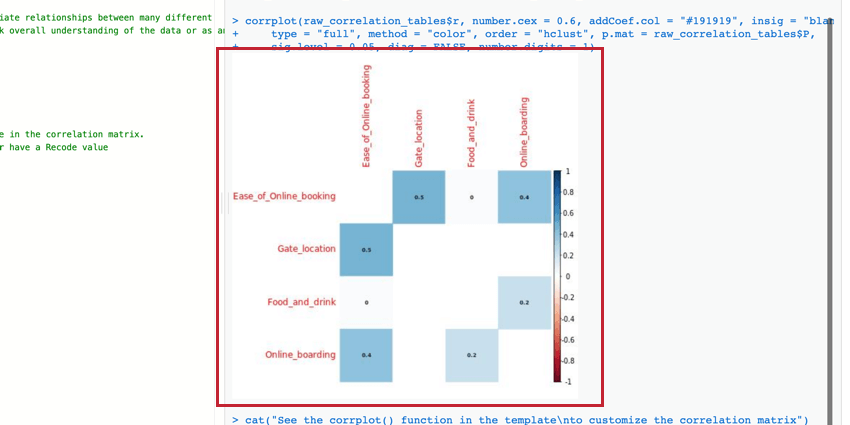
MATRIZ DE CORRELACIÓN ENTRE ÍTEMS
La Matriz de correlación entre ítems muestra la correlación entre cada variable en el análisis y cada otra variable. Por ejemplo, si una variable está altamente correlacionada con otra (por ejemplo, 0,9), esas preguntas pueden ser redundantes y eliminarlas solo tendrá un pequeño impacto en su confiabilidad.
La correlación promedio entre ítems es el promedio de los números en la matriz. Los números más altos sugieren que algunos elementos pueden ser redundantes y podrían eliminarse. Generalmente, las variables deben estar en el rango de 0,2 a 0,4.
MÁS RECURSO
- El análisis de confiabilidad en Stats iQ se ejecuta mediante la función compRelSem() del paquete semTools R. Hay una variedad de configuraciones avanzadas descrito en la documentación. No es necesario utilizar ni comprender estas configuraciones para ejecutar un análisis de confiabilidad.
- La matriz de correlación se ejecuta mediante la función corrplot() del paquete R corrplot. Hay una variedad de configuraciones y personalizaciones avanzadas. descrito en la documentación Y en esto recorrido.
Confiabilidad entre evaluadores
La confiabilidad entre evaluadores (IRR) se utiliza para evaluar en qué medida dos o más evaluadores coinciden en su evaluación. Por ejemplo, tres codificadores diferentes podrían evaluar un comentario de texto como si tuviera un sentimiento positivo, neutral o negativo; el TIR describe en qué medida estuvieron de acuerdo entre sí.
MEDIDAS DE CONFIABILIDAD ENTRE CALIFICADORES
La TIR se evalúa utilizando métricas ligeramente diferentes según la estructura de los datos. Por ejemplo, un análisis de la interconfiabilidad de dos evaluadores utilizará una métrica ligeramente diferente a la de la interconfiabilidad de tres evaluadores.
Stats iQ seleccionará automáticamente la métrica adecuada para sus datos.
INTERPRETACIÓN DE RESULTADOS
La métrica Kappa o ICC es el resultado principal, entre 0 y 1, e indica qué tan bien correlacionados están los evaluadores. Sugerimos los siguientes rangos para interpretar el Kappa:
| 0,75 a 1 | Excelente |
| 0,6 a 0,75 | Bueno |
| 0,4 a 0,6 | Bastante bien |
| 0,4 o inferior | Malo |
MÁS RECURSO
- Este análisis de confiabilidad se ejecuta mediante las funciones del paquete IRR R. Hay una variedad de configuraciones avanzadas descrito en la documentación. No es necesario utilizar ni comprender estas configuraciones para ejecutar este análisis.
Análisis de factores exploratorios
El análisis factorial exploratorio (AFE) es una técnica estadística que ayuda a reducir una gran cantidad de variables a un conjunto más pequeño y manejable de “factores” resumidos. Esto hace que sea mucho más fácil interpretarlos, comunicarlos y ejecutar análisis adicionales (por ejemplo, análisis de regresión). La EFA normalmente sigue este conjunto de pasos:
- Diagnóstico:Ejecutar e interpretar un conjunto de diagnósticos que determinen si los datos son adecuados para el análisis factorial. Las variables deben estar lo suficientemente correlacionadas entre sí para formar agrupaciones significativas, pero no tan altamente correlacionadas que sean esencialmente redundantes.
- Factores de elección:Determinar el número de factores presentes en los datos. Los factores son agrupaciones de variables similares. De forma predeterminada, el script R utilizará un criterio que se calcula y se ejecuta automáticamente.
- Factores de denominaciónDespués de ejecutar el EFA, tendrá varios factores que representan mejor los temas clave en los datos. Es útil etiquetar estos factores con nombres legibles para humanos que capturen su significado.
- Medidas y métricas asociadas:El análisis factorial se ejecuta con el número de factores del paso anterior. El resultado es un conjunto de agrupaciones de variables junto con una descripción estadística de la factorización.
El resultado es un conjunto de factores nombrados y sus elementos de encuesta componentes. Estos factores pueden servir como marco conceptual para análisis posteriores o pueden aplicarse a los datos.
DIAGNÓSTICO
El script primero ejecuta una serie de diagnósticos para garantizar que los datos sean adecuados para EFA:
- Tamaño de la Muestra:Por lo general, se sugiere una proporción de respuestas por ítem de 10:1. Por ejemplo, si tienes 10 preguntas deberías tener al menos 100 encuestados.
- Prueba de esfericidad de Bartlett:Esta prueba evalúa si los elementos están lo suficientemente correlacionados como para ser agrupados de manera útil en factores. Si esto falla, es probable que haya varios elementos que no se correlacionen lo suficiente con los demás. Puede considerar eliminar de su análisis elementos que no se correlacionen con otros o agregar más elementos relacionados a la encuesta.
- Determinante:El determinante evalúa si los elementos están demasiado correlacionados como para ser agrupados de manera útil en factores. Si este diagnóstico falla, es probable que haya elementos que sean demasiado similares entre sí como para separarlos en factores. Considere editar los elementos de la encuesta para que sean más distintivos.
- Medida Kaiser-Meyer-Olkin (KMO):Esta medida verifica si los elementos de su encuesta tienen suficiente en común como para agruparlos en factores significativos. Pasar este diagnóstico significa que las respuestas de su encuesta tienen mucho en común y se pueden agrupar de forma clara. De lo contrario, los elementos no clúster en categorías. Si este diagnóstico falla, es posible que desees revisar los elementos de tu encuesta para capturar temas más similares y considerar eliminar los elementos que no muestren una relación clara con otros.
FACTORES DE ELECCIÓN
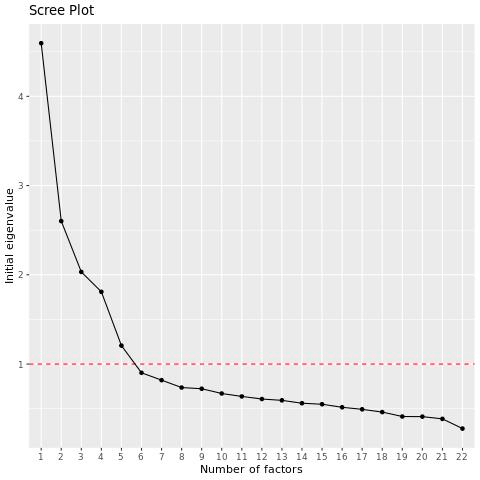
El objetivo del EFA es reducir muchas variables a un número relativamente pequeño que sea útil para el análisis, por lo que es posible que tenga que ejecutar el análisis factorial varias veces con diferentes cantidades de factores para encontrar una agrupación que funcione para usted. El script EFA sugerirá el número de factores utilizando sus valores propios.
El script EFA generará un gráfico de pantalla que muestra los valores propios de las variables en orden descendente. Puede examinar el gráfico para ver cuántos factores ocurren antes del “codo” en el gráfico, después de lo cual agregar más factores es menos útil.
NOMBRAR SUS FACTORES
Después de ejecutar EFA, a cada variable se le asigna un factor. Es útil darle a cada factor un nombre que le permita hablar de ellos de manera abreviada, lo que hace que sus hallazgos sean más accesibles. El objetivo aquí es simplificar sus datos complejos en unos pocos temas comprensibles.
A continuación se presentan algunas pautas para nombrar sus factores:
- Sea descriptivo:Intenta capturar el tema común que resuma las variables del grupo.
- Mantenlo simple:Los nombres de sus factores deben ser fáciles de entender y comunicar. Evite la jerga técnica o frases demasiado complejas.
- Ten en cuenta a tu audienciaLos nombres de los factores deben tener sentido para las personas que utilizarán su análisis. Por ejemplo, “Limpieza” podría tener significado tanto para los gerentes como para los huéspedes del hotel.
- Consistencia:Si su encuesta o conjunto de datos abarca diferentes dominios o temas, asegúrese de que los nombres de sus factores sean consistentes.
MEDIDAS Y MÉTRICAS ASOCIADAS
La tabla de cargas factoriales es uno de los resultados clave del EFA. La carga factorial para un par variable-factor dado es la correlación entre esa variable y ese factor. Si una variable tiene una alta carga factorial para un determinado factor, significa que la pregunta está fuertemente conectada a ese factor.
La unicidad es la parte de la varianza que es única para la variable específica y no se comparte con otras variables. Los valores de unicidad varían de 0 a 1; los valores más altos indican que la variable es única y no encaja bien en ninguno de los factores.
En general, se recomienda eliminar las variables si sus cargas factoriales son superiores a 0,3 o su unicidad es superior a 0,7.
USANDO SUS RESULTADOS
El análisis factorial es un proceso iterativo, por lo que es posible que tengas que ejecutarlo varias veces con diferentes cantidades de factores para encontrar una agrupación que funcione para ti. Para la mayoría de los investigadores, la conclusión clave es encontrar agrupaciones de factores que puedan proporcionar una nueva Insight de sus datos, pero puede utilizar estos factores como nuevas variables en análisis posteriores, como regresión o análisis de clúster. Por ejemplo, podría crear una nueva variable para cada factor que tome el valor promedio de todas las variables que están agrupadas en él.
Matriz de correlación
La matriz de correlación es una tabla que muestra la correlación entre cada par de variables proporcionadas. Esta tabla utiliza la r de Pearson de forma predeterminada para medir la correlación, pero puede cambiarla a la rho de Spearman si lo desea.
Puede editar los parámetros de la función corrplot() para modificar la tabla y hacerla más legible. Para más información, puedes consultar la R oficial Tutorial y documentación.