Análisis de correspondencia (BX)

Acerca del análisis de correspondencia

El análisis de correspondencia revela las relaciones relativas entre y dentro de dos grupos de variables, basándose en los datos dados en una tabla de contingencia. Para las percepciones de la marca, estos dos grupos son:

1. Marcas
2. Atributos que se aplican a estas marcas

Por ejemplo, supongamos que una empresa quiere saber qué atributos asocian los consumidores con diferentes marcas de productos de bebidas. El análisis de correspondencia ayuda a medir las similitudes entre marcas y la fortaleza de las marcas en términos de sus relaciones con diferentes atributos. Comprender las relaciones relativas permite a los propietarios de la marca identificar los efectos de acciones anteriores en diferentes atributos relacionados con la marca y decidir los próximos pasos a seguir.

El análisis de correspondencia es valioso en las percepciones de la marca por un par de razones. Al intentar ver las relaciones relativas entre marcas y atributos, el tamaño de la marca puede tener un efecto engañoso; el análisis de correspondencia elimina este efecto. El análisis de correspondencia también proporciona una vista rápida intuitiva de las relaciones de atributos de marca (basadas en la proximidad y la distancia desde el origen) que no proporcionan muchos otros gráficos.

En esta página, veremos un ejemplo de cómo aplicar análisis de correspondencia a un caso de uso para diferentes marcas (ficticias) de productos de soda.

Comencemos con el formato de datos de entrada, una tabla de contingencia.

Tablas de contingencia

Una tabla de contingencia es una tabla bidimensional con grupos de variables en las filas y columnas. Si nuestros grupos, como se ha descrito anteriormente, fueran marcas y sus atributos asociados, realizaríamos encuestas y obtendríamos recuentos de respuestas diferentes asociando diferentes marcas con los atributos indicados. Cada celda de la tabla representa el número de respuestas o recuentos que asocian ese atributo con esa marca. Esta “asociación” se mostraría a través de una pregunta de la encuesta como “Elegir marcas de una lista debajo de la cual cree que se muestra el atributo ___”.

En este caso, los dos grupos son “Marcas” (líneas) y “Atributos” (columnas). La celda en la esquina inferior derecha representa el recuento de respuestas para la marca “Brawndo” y el atributo “Económico”.

Residuos (R)

En el análisis de correspondencia, queremos ver los residuos de cada celda. Un residual cuantifica la diferencia entre los datos observados y los datos que esperaríamos, suponiendo que no haya relación entre las categorías de fila y columna (en este caso, serían marca y atributo). Un residual positivo nos muestra que el recuento para ese emparejamiento de atributos de marca es mucho más alto de lo esperado, lo que sugiere una relación fuerte; en consecuencia, un residual negativo muestra un valor inferior al esperado, lo que sugiere una relación más débil. Veamos a fondo el cálculo de estos residuos.

Un residual (R) es igual a: R = P – E, donde P es las proporciones observadas y E es las proporciones esperadas para cada célula.  ¡Desglosemos estas proporciones observadas y esperadas!

Proporciones observadas (P)

Una proporción observada (P) es igual al valor de una celda dividido por la suma total de todos los valores de la tabla. Por lo tanto, para nuestra tabla de contingencia anterior, la suma total sería: 5 + 7 + 2 + 18 … + 16 = 312. Dividiendo cada valor de celda por los resultados totales en la tabla siguiente para las proporciones observadas (P).

Por ejemplo, en la celda inferior derecha, tomamos nuestro valor de celda inicial de 16/312 = 0,051. Esto nos indica la proporción de todo nuestro gráfico que el emparejamiento de Brawndo y Economic representa en base a nuestros datos recopilados.

Masas de fila y columna

Algo que podemos calcular fácilmente a partir de nuestras proporciones observadas, y se usará mucho después, son las sumas de las filas y columnas de nuestra tabla de proporciones, que se conocen como las masas de fila y columna. Una masa de fila o columna es la proporción de valores para esa fila o columna. La masa de fila de “Butterbeer”, mirando nuestra tabla de arriba, sería de 0.016 + 0.022 + 0.006, lo que nos da 0.044.

Haciendo cálculos similares, terminamos con:

Proporciones previstas (E)

Las proporciones esperadas (E) serían lo que esperamos ver en la proporción de cada celda, asumiendo que no hay relación entre filas y columnas. Nuestro valor esperado para una celda sería la masa de fila de esa celda multiplicada por la masa de columna de esa celda.

Véase en la celda superior izquierda, la masa de fila para Butterbeer multiplicada por la masa de la columna para Tasty, 0,044 * 0,182 = 0,008.

Ahora podemos calcular nuestra tabla de residuos (R), donde R = P – E. Los valores residuales cuantifican la diferencia entre nuestras proporciones de datos observadas y nuestras proporciones de datos esperadas si asumimos que no hay relación entre las filas y las columnas.

Tomando nuestro valor más negativo de -0.045 para Squishee y Economic, lo que interpretaríamos aquí es que hay una asociación negativa entre Squishee y Economic; Squishee es mucho menos probable que sea visto como “económico” que nuestras otras marcas de bebidas.

Residuos indexados (I)

Sin embargo, hay algunos problemas con la lectura de los residuos.

Si observamos la fila superior de nuestra tabla de cálculo de residuos anterior, vemos que todos estos números están muy cerca de cero. No deberíamos tomar la conclusión obvia de esto de que Butterbeer no está relacionada con nuestros atributos, ya que esta suposición es incorrecta. La explicación real sería que las proporciones observadas (P) y las proporciones esperadas (E) son pequeñas porque, como nos dice nuestra masa hilera, sólo el 4,4% de la muestra son Butterbeer.

Esto plantea un gran problema al mirar los residuos, ya que ignoramos el número real de registros en las filas y columnas, nuestros resultados se inclinan hacia las filas/columnas con masas más grandes. Podemos arreglarlo dividiendo nuestros residuos por nuestras proporciones esperadas (E), dándonos una tabla de nuestros residuos indexados (I, I = R / E):

Los residuos indexados son fáciles de interpretar: cuanto mayor sea el valor de la tabla, mayor será la proporción observada en relación con la proporción esperada.

Por ejemplo, tomando el valor superior izquierdo, Butterbeer tiene un 95% más de probabilidades de ser visto como “Tasty” que lo que esperaríamos si no hubiera relación entre estas marcas y atributos. Mientras que, al máximo valor, Butterbeer tiene un 65% menos de probabilidades de ser visto como “económico” de lo que esperaríamos, dado que no existe ninguna relación entre nuestras marcas y atributos.

Dados nuestros residuos indexados (I), nuestras proporciones esperadas (E), nuestras proporciones observadas (P) y nuestras masas de filas y columnas, ¡vamos a calcular nuestros valores de análisis de correspondencia para nuestro gráfico!

Calcular coordenadas para análisis de correspondencia

Descomposición de valor singular (SVD)

Nuestro primer paso es calcular la descomposición de valor singular o SVD. El SVD nos da valores para calcular la varianza y trazar nuestras filas y columnas (marcas y atributos).

Calculamos el SVD sobre el residual estandarizado (Z), donde Z = I * sqrt(E), donde I es nuestro residual indexado, y E es nuestras proporciones esperadas. La multiplicación por E hace que nuestro SVD sea ponderado, de modo que a las células con un valor esperado más alto se les da un mayor peso, y viceversa, lo que significa que dado que los valores esperados a menudo están relacionados con el tamaño de la muestra, las células “más pequeñas” en la tabla, donde el error de muestreo habría sido más grande, son ponderadas a la baja. Por lo tanto, el análisis de correspondencia utilizando una tabla de contingencia es relativamente robusto para los valores atípicos causados por el error de muestreo.

De vuelta a nuestro SVD, tenemos: SVD = svd(Z). Una descomposición de valor singular genera 3 salidas:

Un vector, d, que contiene los valores singulares.

Una matriz, u, que contiene los vectores singulares izquierdos (marcas).

Una matriz, v, que contiene los vectores singulares derechos (atributos).

Los vectores singulares izquierdos corresponden a las categorías en las filas de la tabla, y los vectores singulares de la derecha corresponden a las columnas. Cada uno de los valores singulares, para calcular la varianza, y los vectores correspondientes (es decir, columnas de u y v), para trazar posiciones, corresponden a una dimensión. Las coordenadas utilizadas para representar categorías de fila y columna para nuestro gráfico de análisis de correspondencia se derivan de las dos primeras dimensiones.

Variación expresada por nuestras dimensiones

Los valores cuadrados singulares se conocen como autovalores (d^2). Los valores propios en nuestro ejemplo son 0,0704, 0,0129 y 0,0000. Expresar cada autovalor como una proporción de la suma total nos indica la cantidad de varianza capturada en cada dimensión de nuestro análisis de correspondencia, basado en el valor singular de cada dimensión; obtenemos el 84,5% de la varianza expresada por nuestra primera dimensión, y el 15,5% en nuestra segunda dimensión (nuestra tercera dimensión explica el 0% de la varianza).

Análisis de correspondencia estándar

Ahora estamos equipados con los recursos para calcular la forma básica de análisis de correspondencia, utilizando lo que se conoce como coordenadas estándar, calculadas a partir de nuestros vectores singulares izquierdo y derecho. Anteriormente, ponderábamos los residuos indexados antes de realizar el SVD. Con el fin de obtener coordenadas que representen nuestros residuos indexados, ahora necesitamos desponderar las salidas del SVD, dividiendo cada fila de los vectores singulares izquierdos por la raíz cuadrada de las masas de la fila, y dividiendo cada columna de los vectores singulares de la derecha por la raíz cuadrada de las masas de la columna, obteniéndonos las coordenadas estándar de las filas y columnas para el trazado.

Coordenadas estándar de la marca:

Coordenadas estándar de atributo:

Utilizamos las dos dimensiones con la mayor varianza capturada para el trazado, la primera dimensión que va en el eje X y la segunda dimensión en el eje Y, generando nuestro gráfico de análisis de correspondencia estándar.

Hemos establecido las bases de los cálculos que necesitamos para el análisis de correspondencia estándar. En la siguiente sección exploraremos las ventajas y desventajas de los diferentes estilos de análisis de correspondencia, y cuáles se adaptan mejor a nuestros objetivos de ayudar en el análisis de las percepciones de la marca.

Tipos de análisis de correspondencia

Análisis de correspondencia principal de fila/columna

El análisis de correspondencia estándar es fácil de calcular y se pueden obtener resultados sólidos a partir de él. Sin embargo, la correspondencia estándar es una mala elección para nuestras necesidades; las distancias entre las coordenadas de fila y columna son exageradas, y no hay una interpretación directa de las relaciones entre las categorías de fila y columna. Lo que queremos para interpretar las relaciones entre las coordenadas de fila (marca), e interpretar las relaciones entre las categorías de fila y columna, es la normalización principal de fila (o, si nuestras marcas estaban en nuestras columnas, la normalización principal de columna).

Para la normalización principal de fila, desea utilizar las coordenadas estándar calculadas anteriormente para sus valores de columna (atributo), pero desea calcular las coordenadas principales para sus valores de fila (marca). Calcular las coordenadas principales es tan simple como tomar las coordenadas estándar, y multiplicarlas por sus correspondientes valores singulares (d). Por lo tanto, para nuestras filas, solo queremos multiplicar nuestras coordenadas de fila estándar por nuestros valores singulares (d), que se muestran en la tabla siguiente. Para la normalización principal de columna simplemente multiplicaríamos nuestras columnas en lugar de nuestras filas por nuestros valores singulares (d).

Sustituyendo en nuestras coordenadas principales por nuestras filas (marcas), terminamos con:

Debido a que escalamos por nuestros valores singulares, nuestras coordenadas principales para nuestras filas representan la distancia entre los perfiles de fila de nuestra tabla original; uno puede interpretar las relaciones entre nuestras coordenadas de fila en nuestro gráfico de análisis de correspondencia por su proximidad entre sí.

La distancia entre nuestras coordenadas de columna, ya que se basan en coordenadas estándar, son aún exageradas. Además, nuestra escala por nuestros valores singulares en solo una de las dos categorías (filas/columnas) nos ha dado una forma de interpretar las relaciones entre las categorías de fila y columna. Dado un valor de fila y un valor de columna, por ejemplo, Butterbeer (fila), y Tasty (columna), cuanto más larga sea su distancia al origen, más fuerte será su asociación con otros puntos en el mapa. Además, cuanto más pequeño es el ángulo entre los dos puntos (Butterbeer y Tasty), mayor es la correlación entre los dos.

La distancia al origen combinada con el ángulo entre los dos puntos es el equivalente a tomar el producto punto; el producto punto entre un valor de fila y columna mide la fuerza de la asociación entre los dos. De hecho, cuando la primera y la segunda dimensión explican toda la varianza en los datos (suman 100%), el producto punto es directamente igual al residual indexado de las dos categorías. Aquí, el producto de punto sería la distancia al origen de los dos puntos multiplicados por el coseno del ángulo entre ellos; .59*2,12*cos(41) = .94. Teniendo en cuenta los errores de redondeo, es el mismo que nuestro valor residual indexado de 0,95. Por lo tanto, los ángulos menores de 90 grados representan un residuo indexado positivo y, por lo tanto, una asociación positiva, y los ángulos mayores de 90 grados representan una asociación residual o negativa indexada negativa.

Análisis de correspondencia principal de fila escalada

Si miramos nuestro gráfico anterior para la normalización principal de las filas, tenemos una observación fácil: los puntos de nuestras columnas (rasgos) están mucho más dispersos y nuestros puntos para nuestras filas (marcas) están agrupados en clústeres alrededor del origen. Esto puede hacer que el análisis de nuestro grafo a ojo sea bastante difícil y poco intuitivo, y a veces imposible leer las categorías de fila si se solapan. Por suerte, hay una manera fácil de escalar nuestro grafo para traer nuestras columnas, al tiempo que se mantiene la capacidad de utilizar el producto punto (distancia de origen y ángulo entre puntos) para analizar las relaciones entre nuestros puntos de fila y columna, conocida como normalización principal de fila escalada.

La normalización principal de la fila escalada toma la normalización principal de la fila, y escala las coordenadas de columna de la misma manera en que escalamos el eje x de las coordenadas de fila; en otras palabras, nuestras coordenadas de columna se escalan por el primer valor de nuestros valores singulares (d). Nuestros valores de fila permanecen iguales a la normalización principal de la fila, pero ahora nuestras coordenadas de columna se reducen por un factor constante.

Lo que esto significa para nosotros es que nuestras coordenadas de columna se escalan para encajar mucho mejor con nuestras coordenadas de fila, lo que facilita mucho el análisis de tendencias. Debido a que escalamos todas nuestras coordenadas de columna por el mismo factor constante, contrajmos la dispersión de nuestras coordenadas de columna en el mapa, pero no hicimos ningún cambio en sus relatividades; todavía utilizamos el producto punto para medir la fuerza de las asociaciones. El único cambio es que cuando nuestra primera y segunda dimensión cubren toda la varianza en los datos, en lugar de que el residuo indexado sea igual al producto punto de las dos categorías, ahora es igual al producto de punto escalado de las dos categorías, que es el producto de puntos escalado por un valor constante de nuestro primer valor singular (d). La interpretación del gráfico sigue siendo la misma que la normalización principal de la fila.

Análisis de correspondencia principal

Una forma final de análisis de correspondencia que mencionaremos es el análisis de correspondencia principal, también conocido como mapa simétrico, escalado francés o análisis de correspondencia canónica. En lugar de solo multiplicar las filas o columnas estándar por los valores singulares (d) como en el análisis de correspondencia principal fila/columna, multiplicamos ambos por los valores singulares. Por lo tanto, nuestros valores de columna estándar, multiplicados por los valores singulares, se convierten en:

Poner estos junto con nuestros valores de fila calculados en el análisis principal de fila, obtenemos:

El análisis de correspondencia canónica escala las coordenadas de fila y columna por los valores singulares. Lo que esto significa es que podemos interpretar nuestras relaciones entre nuestras coordenadas de fila como lo hicimos en la fila análisis de correspondencia principal (basado en la proximidad), Y podemos interpretar nuestras relaciones entre nuestras coordenadas de columna de manera similar al análisis de correspondencia principal de columna; podemos analizar relaciones entre marcas y relaciones entre atributos. También perdemos la agrupación en clústeres de fila/columna en el centro del mapa del análisis principal de fila/columna. Sin embargo, lo que perdemos del análisis de correspondencia canónica, es una forma de interpretar las relaciones entre nuestras marcas y atributos, algo muy útil en las percepciones de la marca.

Comparación simultánea

Análisis de correspondencia estándar

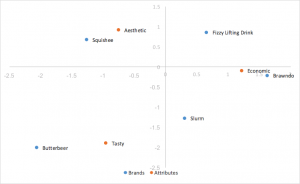
El estilo más fácil de análisis de correspondencia para calcular, utilizando vectores singulares izquierdo y derecho de SVD dividido por las masas de fila y columna. Las distancias entre las coordenadas de fila y columna son exageradas, y no hay una interpretación directa de las relaciones entre las categorías de fila y columna.

Análisis de correspondencia de normalización principal de fila

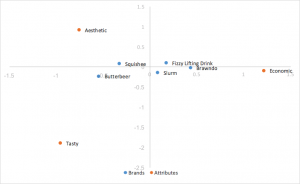
Utiliza coordenadas estándar de arriba, pero multiplica las coordenadas de fila por los valores singulares para normalizar. Las relaciones entre filas (marcas) se basan en la distancia entre ellas. Las distancias de columna (atributo) aún son exageradas. Las relaciones entre filas y columnas se pueden interpretar por el producto punto. Las filas (marcas) tienden a ser agrupadas en el centro.

Análisis de correspondencia de normalización principal de fila escalada

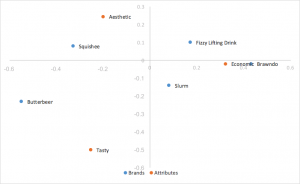
Toma en fila la normalización principal y escala las coordenadas de columna por una constante del primer valor singular. Mismas interpretaciones dibujadas como normalización principal de fila, reemplazando producto punto por producto punto escalado. Ayuda a eliminar agrupación de filas en el centro. Este es el estilo de análisis de correspondencia que preferimos.

Análisis de correspondencia de normalización principal (simétrico, mapa francés, canónico)

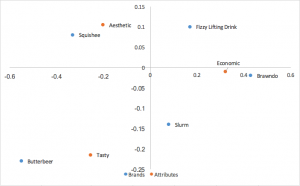
Otra forma popular de análisis de correspondencia usando coordenadas normalizadas principales en las filas y columnas. Las relaciones entre filas (marcas) se pueden interpretar por distancia entre sí; lo mismo se puede decir para las columnas (atributos). No se puede dibujar ninguna interpretación para las relaciones entre filas y columnas.

Tratamiento posterior

En conclusión, el análisis de correspondencia se utiliza para analizar las relaciones relativas entre y dentro de dos grupos; en nuestro caso, estos grupos serían marcas y atributos.

El análisis de correspondencia elimina un sesgo en los resultados de diferentes masas entre grupos mediante el uso de residuos indexados. Para las percepciones de marca para el análisis de correspondencia, utilizamos la normalización de fila principal (o columna principal si las marcas están colocadas en las columnas), ya que esto nos permite analizar las relaciones entre diferentes marcas por su proximidad entre sí, y también nos permite analizar las relaciones entre marcas y atributos por su distancia del origen combinado con el ángulo entre ellas y el origen (el producto punto), en el sacrificio de tergiversar la relación entre atributos con relaciones exageradas que no nos distan. Utilizamos la normalización principal de fila/columna escalada para que sea más fácil analizar nuestro gráfico sin coste alguno. Queremos asegurarnos de tener en cuenta que sumamos la varianza explicada de las etiquetas de los ejes X e Y (la primera y la segunda dimensión) para ver la varianza total capturada en el mapa; cuanto menor sea este número, más inexplicable será la varianza existente en los datos y más engañosa será la gráfica.

Una última cosa a recordar es que el análisis de correspondencia solo muestra relatividades ya que eliminamos el factor de masa de nuestros datos; nuestro gráfico no nos dirá nada sobre qué marcas tienen las puntuaciones “más altas” en atributos. Una vez que comprende cómo crear y analizar los gráficos, el análisis de correspondencia es una herramienta poderosa que ignora los efectos de dimensionamiento de la marca para brindar información estratégica poderosa y fácil de interpretar sobre las relaciones entre y dentro de las marcas y sus atributos aplicables.

Preguntas frecuentes