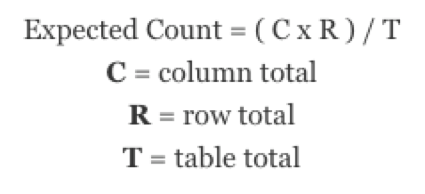Statistiken verstehen

Über Statistiken

Willkommen bei Qualtrics Statistics. Dies ist eine Übersicht über grundlegende Statistiken, die für Sie beim Erstellen und Analysieren von Projekte in Qualtrics hilfreich sein können. Wir werden einige grundlegende statistische Konzepte abdecken, diese auf die Plattform übernehmen und einige weitere Optionen außerhalb von Qualtrics besprechen.

Quantitative und kategorische Daten

Es gibt zwei Arten von Daten: quantitativ und kategorisch.

Quantitative Daten werden auf einer numerischen Skala bewertet. Beispiele für quantitative Daten sind Alter, Höhe oder Einkommen.

Kategorische Daten werden auf einer nominalen Skala bewertet. Beispiele für kategorische Daten sind Geschlecht, Familienstand oder Beruf. Die meisten in einer Umfrage erfassten Daten sind kategorisch, wobei die Anzahl der Umfrageteilnehmer, die in eine Kategorie fallen, ermittelt wird.

Kennzahlen des Zentrums

Für quantitative Daten werden drei Zentrumskennzahlen verwendet: Mittelwert, Median und Modus.

Der Mittelwert oder Durchschnitt ist das beste Maß für das Zentrum, wenn Daten ungefähr normal verteilt sind oder wie eine Glockenkurve aussehen. Der Mittelwert wird ermittelt, indem alle Beobachtungen addiert und durch die Gesamtzahl der Beobachtungen dividiert werden.

Der Median oder Mittelwert ist ein gutes Maß für das Zentrum, wenn Daten scheinbar verzerrt sind. Wenn Sie alle Ihre Beobachtungen in der richtigen Reihenfolge anordnen, ist der Median der mittlere Wert.

Der Modus ist der Wert, der am häufigsten in Ihren Daten vorkommt. Es wird nicht so häufig verwendet wie der Mittelwert oder der Median.

Verbreitungsmaße

Es gibt einige nützliche Statistiken, um die Verteilung Ihrer Daten zu messen: Standardabweichung, Abweichung und Bereich.

Eine Standardabweichung ist der durchschnittliche Abstand der Beobachtungen von ihrem Mittelwert. Wie der Mittelwert sollte eine Standardabweichung mit grob normal verteilten Daten verwendet werden.

Die Abweichung ist einfach die Standardabweichung zum Quadrat.

Der Bereich ist die Differenz zwischen dem größten und dem kleinsten Wert.

Statistiken in Visualisierungen

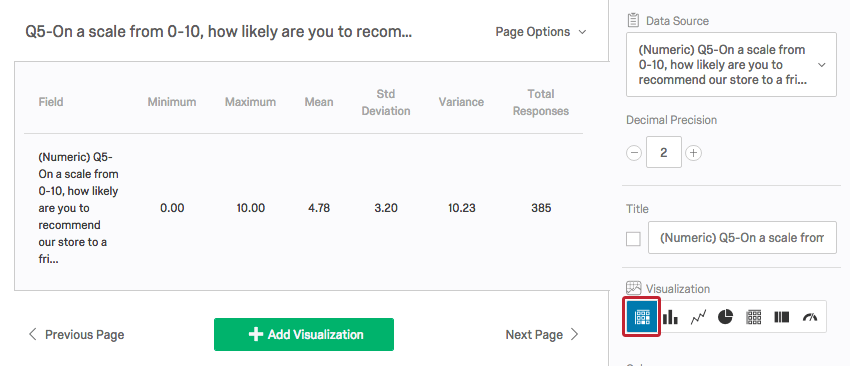
Eine Visualisierung der Statistiktabelle in Qualtrics zeigt den Mindestwert, den Höchstwert, den Mittelwert, die Abweichung, die Standardabweichung und die Gesamtzahl der Antworten an.

Da für jede Antwortoption in jeder Frage ein Wert kodiert ist, findet Qualtrics diese Statistiken, unabhängig davon, ob die Daten quantitativ oder kategorisch sind. Es liegt an Ihnen, zu entscheiden, ob diese Statistiken im Rahmen Ihrer Studie sinnvoll sind.

Sie können Umfrageteilnehmer beispielsweise fragen, welche bevorzugte Farbe sie haben: rot, gelb, blau oder grün, kodiert als 1, 2, 3 und 4. Qualtrics gibt Ihnen ein Mittel, aber es ist nicht sinnvoll, eine durchschnittliche Lieblingsfarbe zu haben.

Wenn die Teilnehmer Filme auf einer Skala von 1 bis 5 Sternen bewerten würden, wäre ein Mittelwert nützlich. Das bedeutet 2,98 Sterne oder 4,32 Sterne machen Filme einfach zu vergleichen.

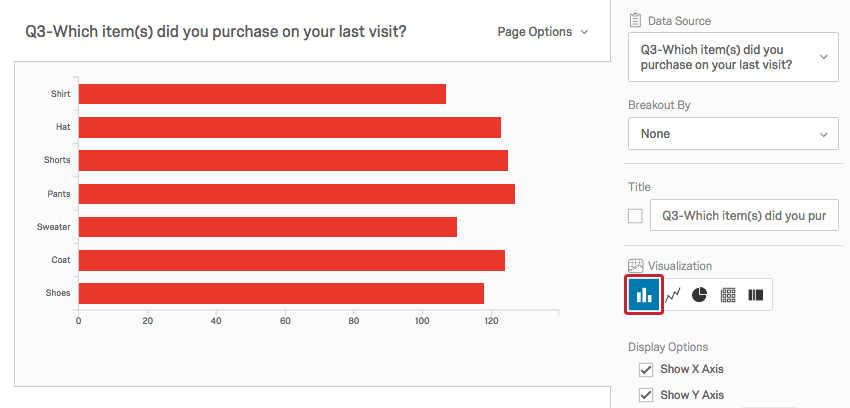
Qualtrics bietet eine Vielzahl von Diagrammen, Grafiken und Tabellen. Ein Balkendiagramm zeigt die Häufigkeit der Antworten in jeder Antwortmöglichkeit an.

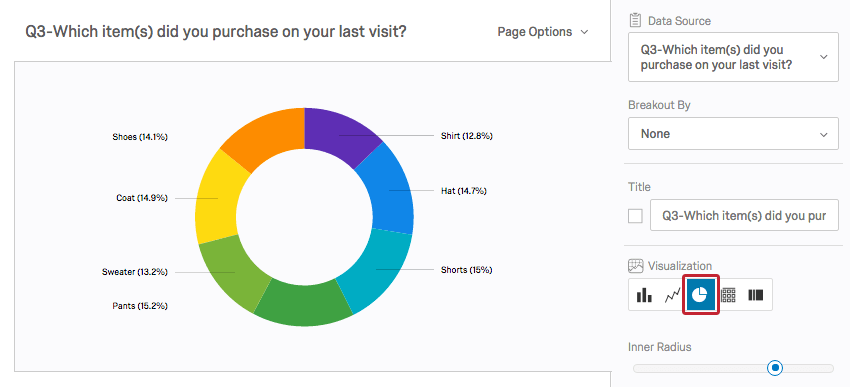
Ein Kreisdiagramm zeigt diese Häufigkeiten als Prozentsatz des Kreisdiagramms an.

Sowohl Balkendiagramme als auch Kreisdiagramme erleichtern den Vergleich der Frequenzen zwischen Kategorien.

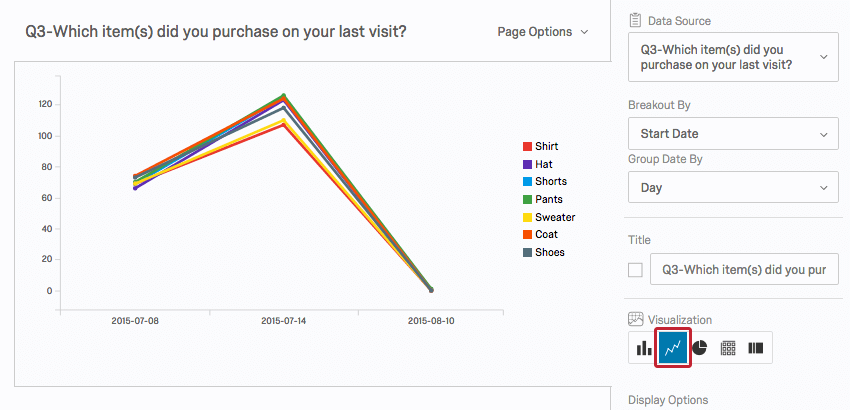
Ein Liniendiagramm ist ein zweidimensionales Streudiagramm für geordnete Beobachtungen. Es ist eine gute Möglichkeit, Trends im Laufe der Zeit zu sehen.

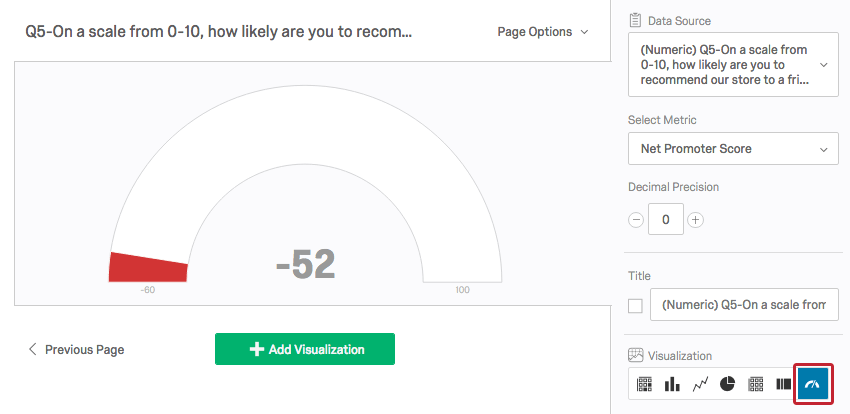
Ein Tachometerdiagramm vergleicht eine ausgewählte Metrik (z. B. Durchschnitt, Summe) mit einer Skala. Je nachdem, wo die Metrik fällt, ändert sich die Farbe der Skala. Messuhrdiagramme sind hilfreich, um die erwartete leistung eines Werts schnell mit der tatsächlichen leistung zu vergleichen.

Kreuztabellen

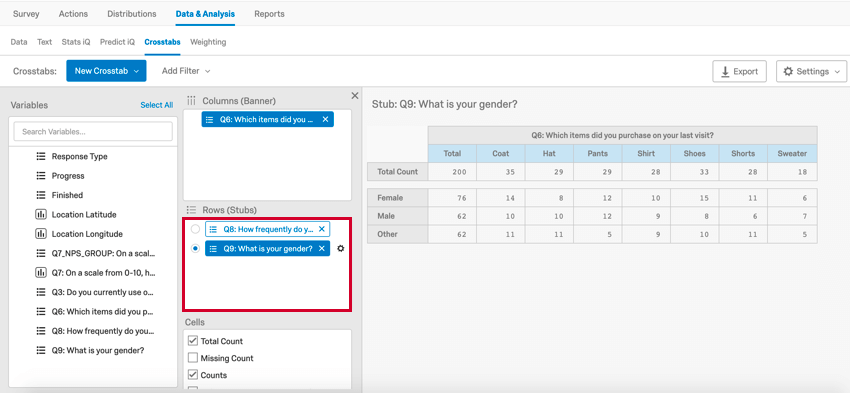
Eine Möglichkeit zur Analyse kategorischer Daten ist eine Kreuztabelle, auch Eventualtabelle oder 2-Wege-Tabelle genannt. Eine Kreuztabelle erfasst die Anzahl der Umfrageteilnehmer mit den spezifischen Merkmalen, die in den Zellen der Tabelle beschrieben sind.

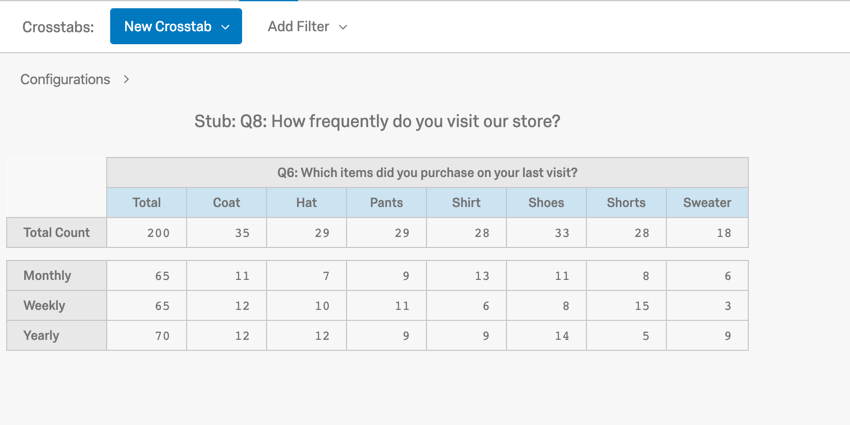
In diesem Beispiel sehen Sie die Anzahl jeder Positionsart, die wöchentlich, monatlich und jährlich gekauft wurde (z.B. werden 11 Schichten monatlich gekauft).

Eine Kreuztabelle besteht aus Spalten und Zeilen bzw. Bannern und Stubs, wobei jedes Banner und jeder Stub Frequenzdaten aus einer Frage abruft. Qualtrics ermöglicht Ihnen nur die Auswahl von Fragen, die für Kreuztabellen kompatibel sind (z. B. sind offene Texteingabe nicht mit Kreuztabellen kompatibel). Wenn Sie mehrere Banner oder Stubs auswählen, können Sie auswählen, welches Banner oder welcher Stub Sie anzeigen möchten, indem Sie im Kreuztabelleneditor darauf klicken. Wenn Sie Ihrer Kreuztabelle einen mehrstufigen Drilldown hinzufügen, wird eine Variable als Unterkategorie einer anderen angezeigt.

CH-Quare-Teststatistik

Die Chi-Quadrat-Teststatistik prüft auf eine signifikante Beziehung zwischen einem Stub und einem Banner.

Wenn Sie mehrere Stubs und Banner in Ihre Kreuztabelle aufnehmen, erstellt Qualtrics auch mehrere Chi-Quadrat-Werte, also 1 für jede Banner- und Stub-Kombination.

Es ist von Vorteil zu wissen, wie eine Chi-Quadrat-Teststatistik berechnet wird. Zunächst müssen Sie die erwartete Anzahl für jede Zelle finden, oder die Anzahl, die die Zelle basierend auf der Zeilensumme, der Spaltensumme und der Tabellensumme erwarten würde. Um eine erwartete Anzahl zu finden, verwenden Sie die Zeilensumme mal die Spaltensumme, und teilen Sie das Ergebnis durch die Tabellensumme.

Führen Sie nach der erwarteten Zählung die folgende Berechnung durch:

Die Chi-Quadrat-Teststatistik wird ermittelt, indem der beobachtete Wert abzüglich des erwarteten Werts genommen, diese Differenz quadriert und durch den erwarteten Wert für jede Zelle dividiert wird. Diese einzelnen chi-quadratischen Testkomponenten werden dann addiert und das Ergebnis ist die Chi-Quadrat-Teststatistik. Der Chi-Quadrat-Wert wird dann verwendet, um zu ermitteln, ob die Beziehung zwischen Ihren Variablen statistisch signifikant ist.

p-Wert

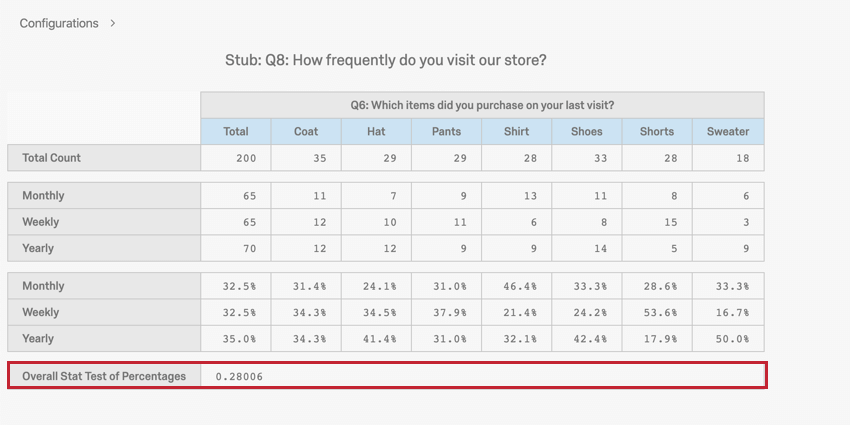
Die Chi-Quadrat-Teststatistik wird zusammen mit dem Ebene verwendet, um einen p-Wert zu finden. Ein p-Wert bestimmt, ob die Zuordnung zwischen den beiden Variablen statistisch signifikant ist. Ein niedriger p-Wert bedeutet, dass die beobachtete Beziehung mit sehr geringer Wahrscheinlichkeit auftreten würde, sodass es eine signifikante Beziehung zwischen den beiden Variablen gibt. Ein niedriger p-Wert wird in der Regel als eine Zahl kleiner als 0,05 betrachtet.

Unser p-Wert ist 0,28, was nicht signifikant ist. Daher gibt es keine Beziehung zwischen der Besuchshäufigkeit und der Art der gekauften Position.

Zusätzliche Analysen

Weitere Analysen für quantitative Daten wie Korrelation und Regression können in Excel oder in ein statistisches Softwarepaket durchgeführt werden.

Korrelation

Der Korrelationskoeffizient r beschreibt die Stärke und Richtung für eine grob lineare Beziehung zwischen 2 quantitativen Variablen. Der Wert von r liegt immer innerhalb von -1 und 1, wobei Werte am nächsten an -1 und 1 eine starke Korrelation darstellen und Werte nahe Null schwach sind. Das Vorzeichen gibt die positive oder negative Richtung der Beziehung an. Korrelationswerte zwischen -.3 und .3 werden als eher niedrig betrachtet, während Korrelationswerte zwischen 0,7 und 1 oder -.7 und -1 als hoch gelten.

Ein wichtiger Punkt, der beachtet werden muss, ist, dass die Korrelation nicht mit der Verursachung übereinstimmt. Nur weil 2 Variablen stark korreliert sind, bedeutet dies nicht, dass eine dieser Variablen dazu führt, dass die andere 1 auftritt.

Regression

Die Regressionsanalyse kann verwendet werden, um Prognosen für eine Variable basierend auf einer oder mehreren Prädiktorvariablen zu erstellen. Weitere Hilfe zu Regressionen finden Sie auf den folgenden Seiten:

• Benutzerfreundlicher Leitfaden für die lineare Regression
• Benutzerfreundlicher Leitfaden zur logistischen Regression

FAQs