Regression und relative Wichtigkeit

Informationen zu Regression und relativer Wichtigkeit

Regression zeigt Ihnen, wie sich mehrere Eingabevariablen zusammen auf eine Ausgabevariable auswirken. Wenn beispielsweise die Eingaben „Jahre als Kunde“ und „Unternehmensgröße“ mit der Ausgabe „Zufriedenheit“ und miteinander korrelieren, können Sie mithilfe der Regression herausfinden, welche der beiden Eingaben für die Schaffung von „Zufriedenheit“ wichtiger war.

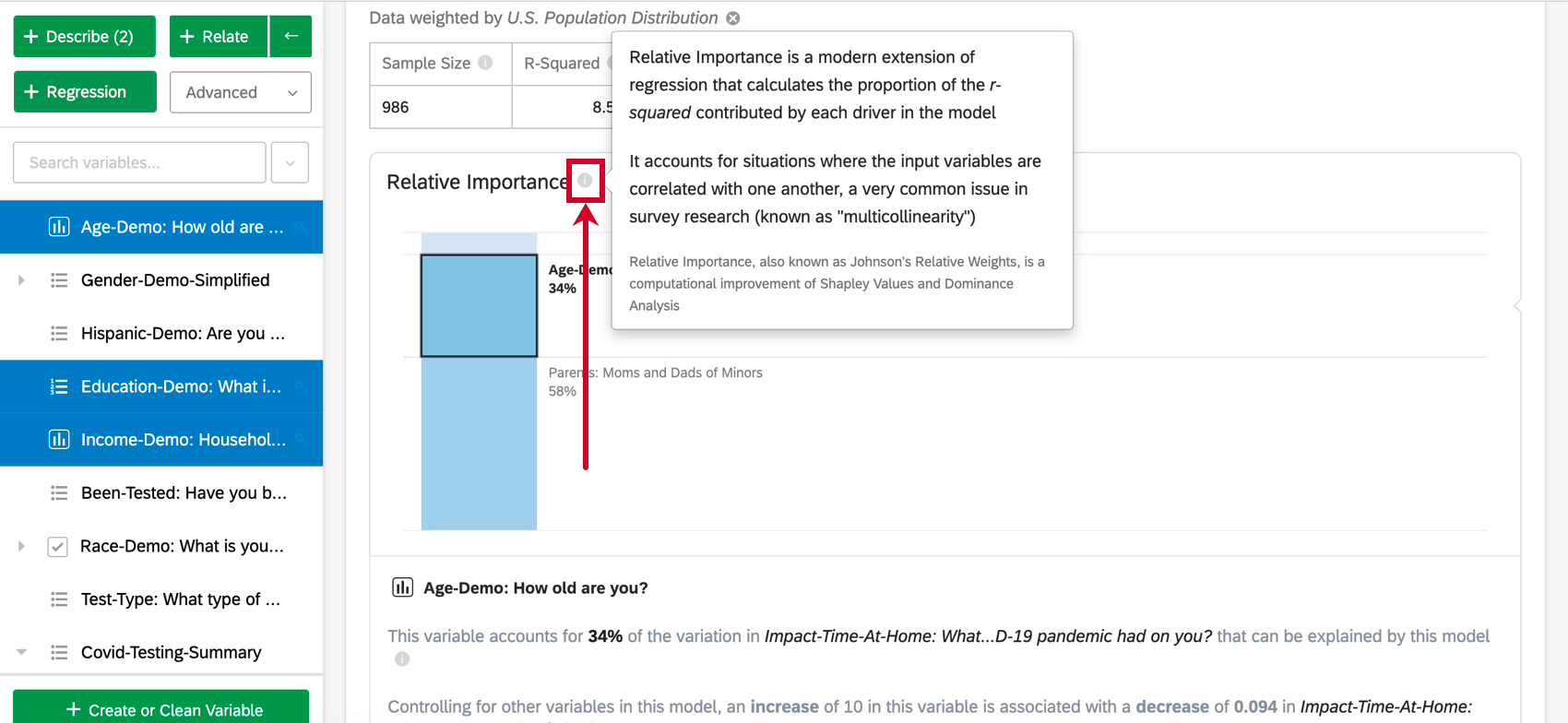
Relative Wichtigkeitsanalyse ist der Best-Practice-Methode für die Regression von Umfrage und die Standardausgabe von Regressionen, die in Stats iQ durchgeführt werden. Relative Wichtigkeit ist eine moderne Erweiterung der Regression, die Situationen berücksichtigt, in denen die Eingabevariablen miteinander korreliert sind, ein sehr häufiges Problem in der Umfrage (bekannt als “Multicollinearity”). Die relative Wichtigkeit wird auch als Johnsons relative Gewichte bezeichnet, ist eine Variation der Shapley-Analyse und steht in engem Zusammenhang mit der Dominanzanalyse.

Nachfolgend finden Sie Anweisungen zum Einrichten einer Regression in Stats iQ. Weitere Informationen zum Durchdenken der analytischen Teile der Regressionsanalyse finden Sie auf den folgenden Seiten:

• Benutzerfreundlicher Leitfaden für die lineare Regression
• Interpretation von Restdiagrammen zur Verbesserung Ihrer linearen Regression
• Benutzerfreundlicher Leitfaden zur logistischen Regression
• Die Matrix und der Precision-Recall-Tradeoff in der logistischen Regression

Tipp: Auf der Stats iQ jetzt hilfreiche Tooltips! Während Sie in Stats iQ arbeiten, können Sie auf das i Symbole, die auf der gesamten Plattform angezeigt werden, um zusätzliche Informationen und Definitionen anzuzeigen.

Für die lineare Regression folgt die relative Wichtigkeit in Stats iQ den in beschriebenen Techniken. Lipovetsky, Stan & Conklin, Michael. (2001). In: Analysis of Regression in Game Theory Approach. Angewandte stochastische Modelle in Wirtschaft und Industrie. 17. 319 – 330. 10.1002/asmb.446.

Variablen für Regressionskarten auswählen

Wenn Sie eine Regressionskarte erstellen, können Sie nachvollziehen, wie sich die Werte anderer Variablen auf den Wert einer Variablen in Ihrem Datenset auswirken.

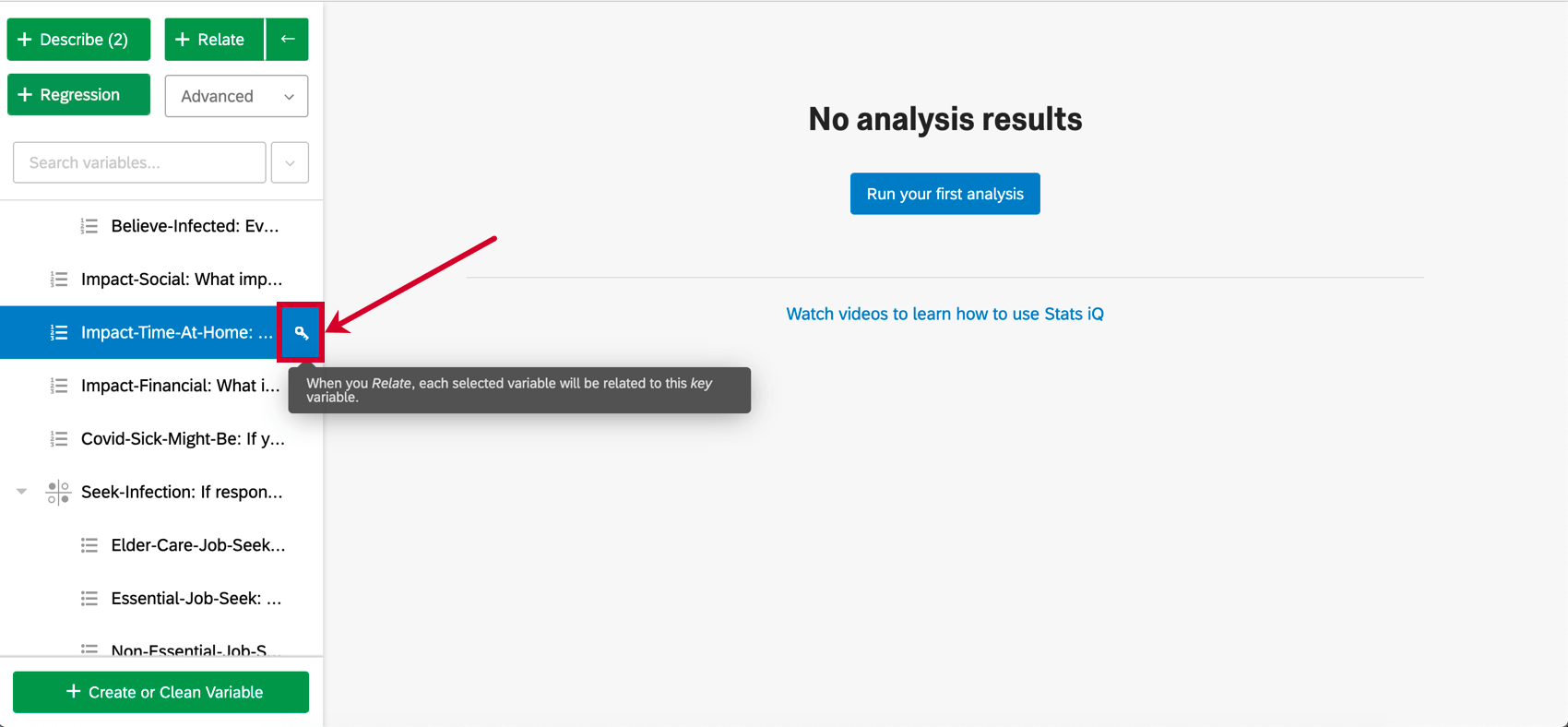
Bei der Auswahl von Variablen enthält eine Variable einen Schlüssel. Für die Regression ist die Schlüsselvariable die Ausgabevariable. Jede andere Variable, die nach der Schlüsselvariable ausgewählt wird, ist eine Eingabevariable. Mit anderen Worten, wir versuchen zu erklären, wie der Wert der Ausgabevariablen von den Eingabevariablen gesteuert wird.

Bei der Auswahl von Variablen für die Regression sind folgende Punkte zu beachten:

• Sie können die Schlüsselvariable ändern, indem Sie auf das Schlüsselsymbol weiter einer beliebigen Variable im Variablenbereich klicken.
• Wenn mehr Variablen als die Anzahl der Antworten ausgewählt sind, wird die Regression nicht ausgeführt.
• Sie können bis zu 25 Eingabevariablen auswählen. Sie sollten jedoch versuchen, 1-10 Eingabevariablen auszuwählen, oder Ihre Ergebnisse könnten sehr kompliziert werden.

Wenn Sie eine große Anzahl von Variablen in eine Analyse einbeziehen möchten, gehen Sie wie folgt vor:

• Führen Sie einige initiale Regressionen aus, und schließen Sie die Variablen aus, die im Modell eine sehr geringe Bedeutung haben.
• Kombinieren Sie mehrere Variablen, indem Sie sie beispielsweise im Durchschnitt darstellen.
• Wenn die Struktur Ihrer Daten dies zulässt, können Sie einen zweistufigen relativen Wichtigkeitsprozess verwenden, wie beschrieben. auf Seite 341 hier.

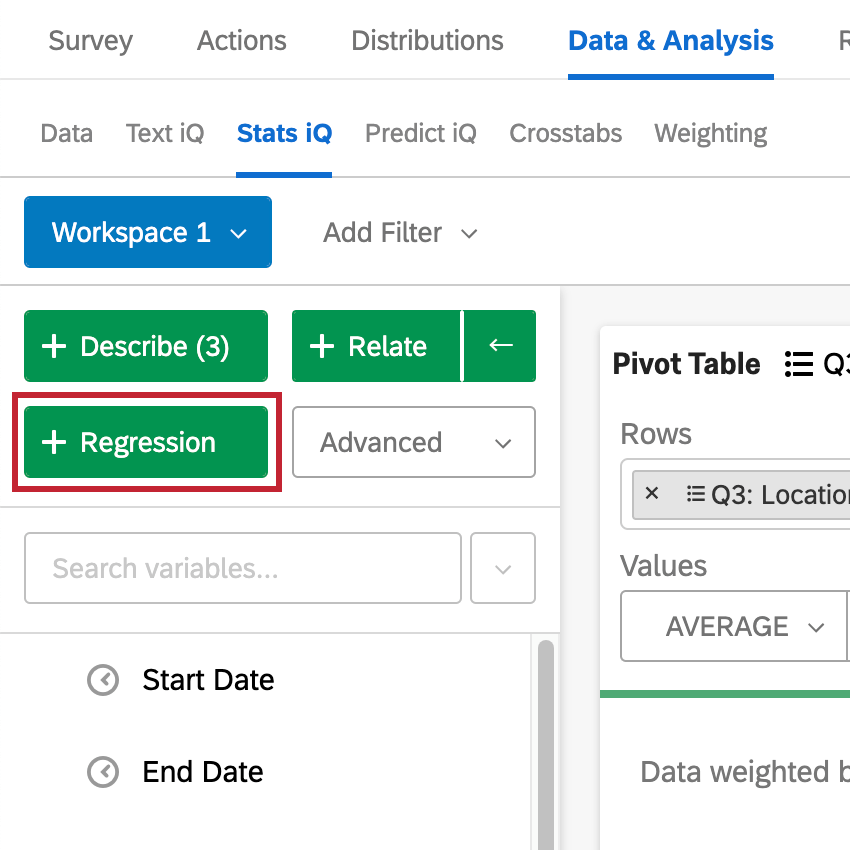
Nachdem Sie Ihre Variablen ausgewählt haben, klicken Sie auf Regression um eine Regression auszuführen.

Regressionsarten

Es gibt zwei Haupttypen von Regressionsläufen in Stats iQ. Wenn die Ausgabevariable eine Zahlenvariable ist, führt Stats iQ eine lineare Regression. Wenn die Ausgabevariable eine Kategorienvariable ist, führt Stats iQ eine logistische Regression.

Genauer gesagt sind die Regressionsarten, die Stats iQ ausführt, wie folgt:

Lineare Regression

Relative Wichtigkeit wird mit Ordinary Least Squares (OLS) kombiniert. Die Ausgabe ergibt sich aus einer Kombination der beiden Analysen:

• Relative Wichtigkeit: Alles in diesem Abschnitt stammt aus der relativen Wichtigkeit mit Ausnahme des R-Quadrats, das aus der OLS-Regression stammt.
• Modell im Detail erkunden: Alles in diesem Abschnitt stammt aus der relativen Wichtigkeit, mit Ausnahme der Verteilungen, die aus den Daten selbst abgerufen werden.
• OLS-Regressionsdiagnosen und -Residuen analysieren, um Ihr Modell zu verbessern: Alles in diesem Abschnitt stammt aus der OLS-Regression.

Logistische Regression

Die logistische Regression ist eine binäre Klassifikationsmethode, die zum Verständnis der Treiber einer Binärdatei (z. Ja oder Nein) bei einer Reihe von Eingabevariablen. Wenn Sie eine Regression für eine Ausgabevariable mit mehr als zwei Gruppen ausführen, wählt Stats iQ eine Gruppe aus und gruppiert die anderen zusammen, um sie zu einer binären Regression zu machen (Sie können ändern, welche Gruppe nach der Ausführung der Regression analysiert wird).

Relative Wichtigkeit

Eingabevariablen in Umfrage sind häufig stark miteinander korreliert; dies ist ein Problem, das als „Multicollinearity“ bezeichnet wird. Dies kann zu einer Regressionsausgabe führen, die die Wichtigkeit einer Variablen künstlich erhöht und die Wichtigkeit einer anderen korrelierten Variablen verringert. Die relative Wichtigkeit wird als Best-Practice-Methode erkannt, um dies zu Benutzerkonto.

Die relative Wichtigkeit (insbesondere die relativen Gewichtungen von Johnson) leidet nicht unter diesem Problem und gleicht die Wichtigkeit der Eingabevariablen angemessen aus, unabhängig davon, welche Art von Regression ausgeführt wird.  Außerdem wird die relative Gewichtung (oder relative Wichtigkeit) jeder Variable berechnet, der Anteil der erklärbaren Variation in der Ausgabe aufgrund dieser Variable. Dies wird als eine Reihe von Prozentsätzen angezeigt, die sich zu 100 % addieren.

Sie gibt Ergebnisse wie die Ausführung einer Reihe von Regressionen zurück, eine für jede Variation der Eingabevariablen. Wenn Sie beispielsweise zwei Variablen hätten, würde dies der Ausführung von drei Regressionen gleichwertig sein: eine mit Variable A, eine mit Variable B und eine mit beiden. Auf diese Weise kann sie die Wichtigkeit jeder Variablen quantifizieren und diese Quantifizierung auf das Regressionsergebnis übernehmen.

Regressionsausgabe

Wenn Sie eine Regression in Stats iQ ausführen, enthalten die Ergebnisse die folgenden Abschnitte:

Numerische Zusammenfassung

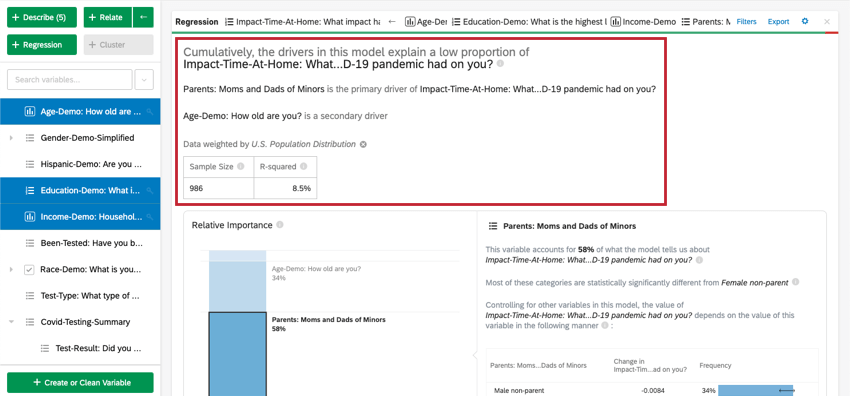
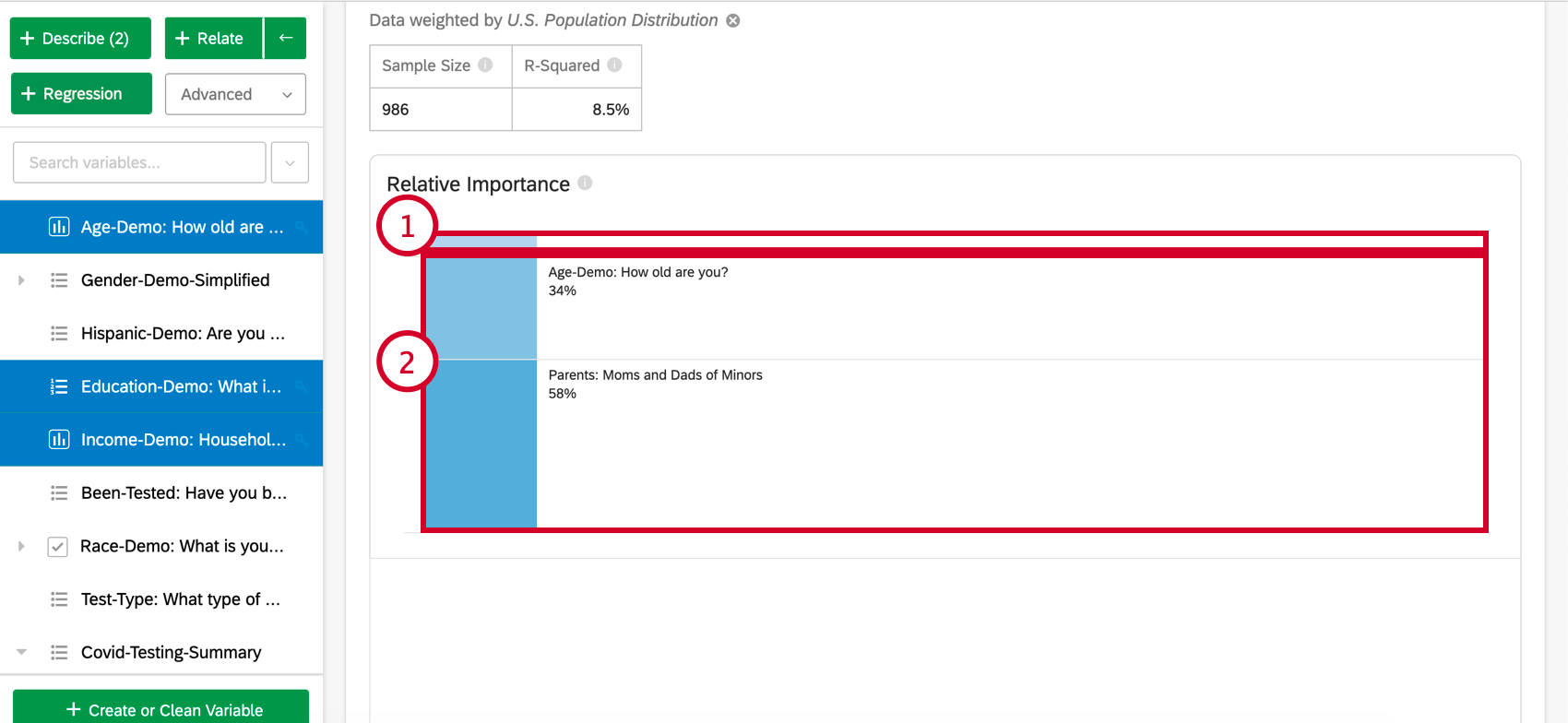
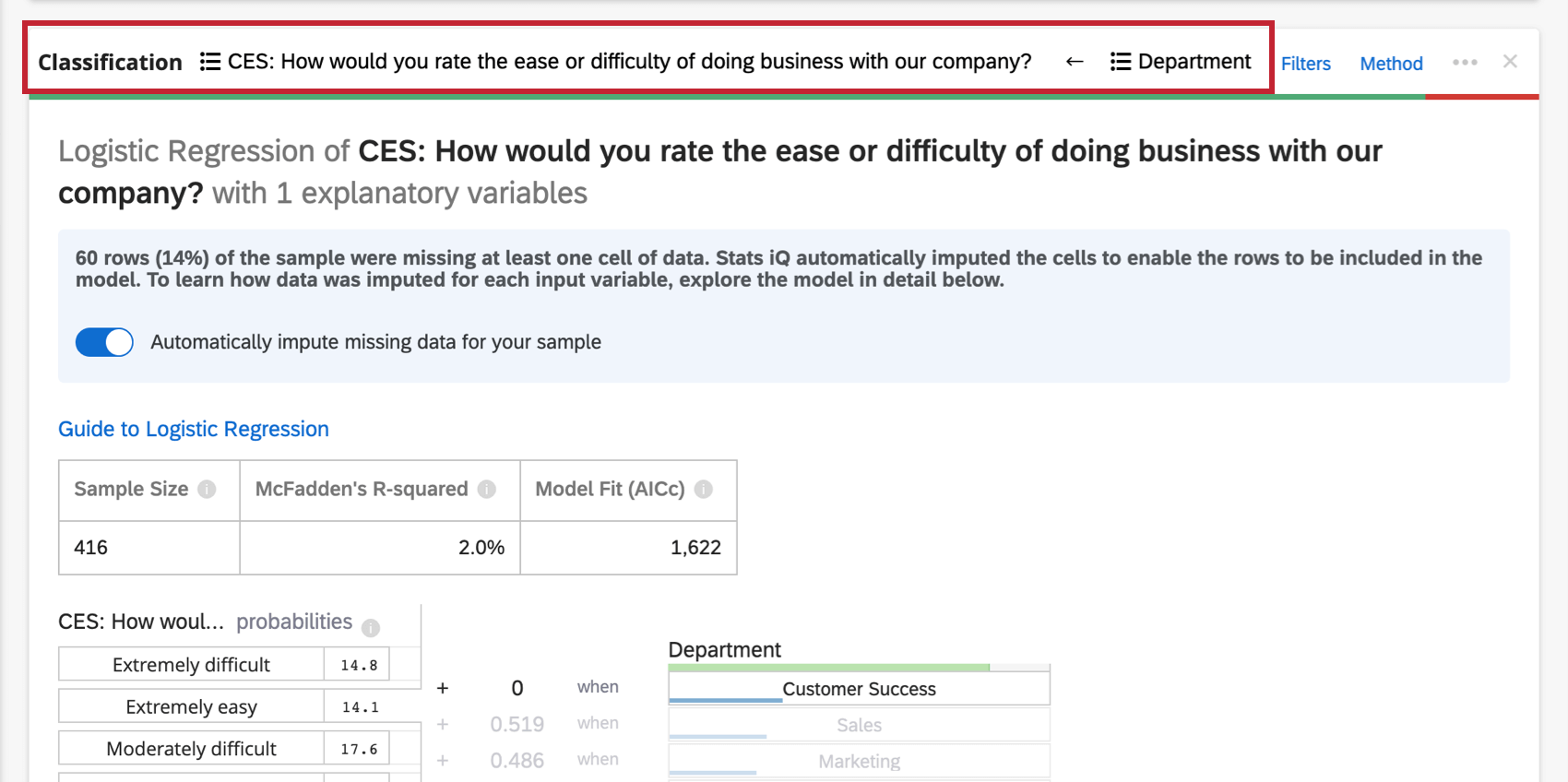
Oben auf der Karte befindet sich eine Zusammenfassung für die Regressionsanalyse. Betrachtet man die ausgewählten Variablen, erklärt diese schriftliche Zusammenfassung, welche Variablen die primären vs. sekundären Treiber sowie Treiber mit geringen kumulativen Auswirkungen sind. Die Datentabelle enthält den Stichprobe und den R-Quadrat-Wert.

Relative Wichtigkeit

1. Variablen mit geringer Auswirkung: Variablen, die einzeln eine relative Wichtigkeit von 10 % oder weniger haben, werden gruppiert. Wenn diese Option ausgewählt ist, gibt es einen Abschnitt, in dem die relative Wichtigkeit und die statistische Signifikanz jeder Variablen mit geringer Auswirkung erläutert werden.
2. Variablen mit hoher Auswirkung: Jede Variable mit hoher Auswirkung ist separat und anklickbar. Sobald eine Variable ausgewählt wurde, können Sie unterhalb des Balkendiagramm die berücksichtigte Variation anzeigen und was passieren würde, wenn andere Variablen im Modell gesteuert würden.

Zusätzliche Modelldetails

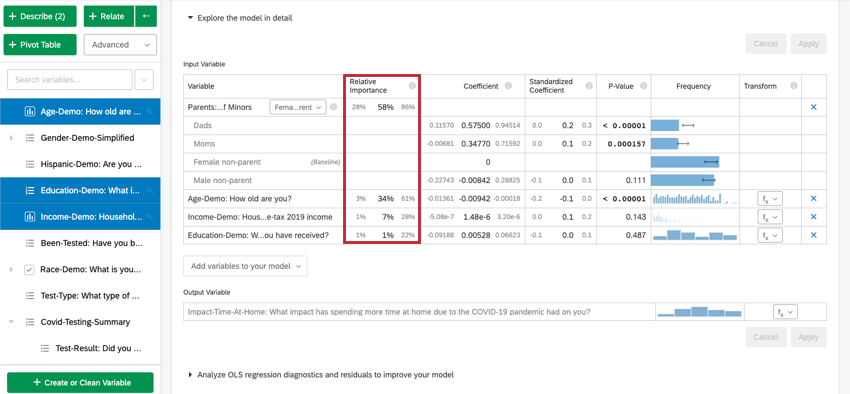
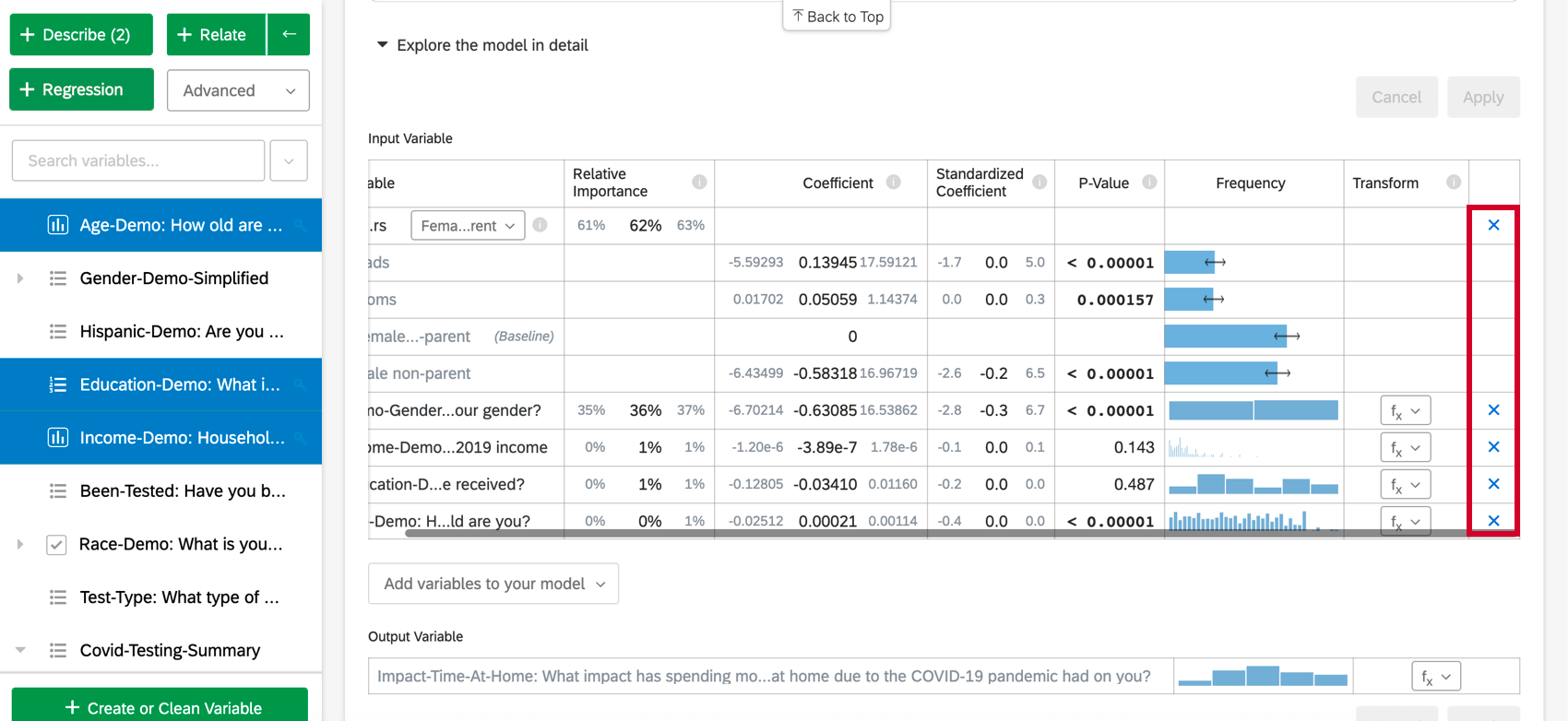
Wenn Sie Modell im Detail erkundenwerden Ihre Eingabevariablen und Ihre Ausgabevariablen aufgelistet. Ihre Eingabevariablen enthalten die folgenden Informationen:

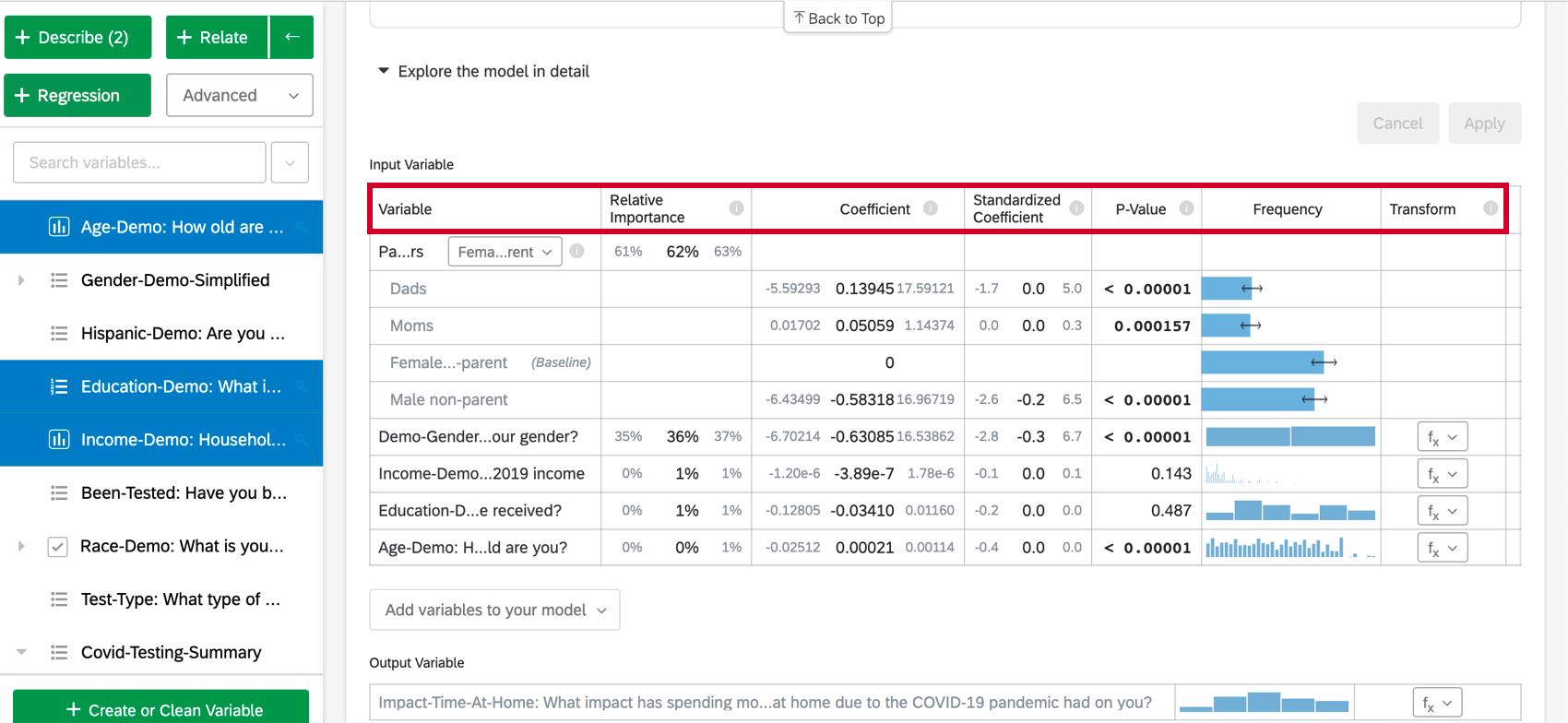
• Relative Wichtigkeit: Der Anteil des R-Quadrats, der durch eine einzelne Variable beigetragen wird. Das R-Quadrat ist der Anteil der Variation der Ergebnisvariablen, der durch die Eingabevariablen in diesem Modell erklärt werden kann. Siehe Relative Wichtigkeit für weitere Details.
• Quotenverhältnis: Nur relevant für logistische Regression. Das Quotenverhältnis für eine bestimmte Eingabevariable gibt den Faktor an, um den sich die Chancen für jede Einheitserhöhung in der erklärenden Variablen ändern.
  Beispiel: Beispiel: Wenn das Quotenverhältnis für Zufriedenheit mit Manager:in 1.1 ist und die Gruppen der Ausgabevariablen Zufrieden und Nicht zufrieden, dann für jede Instanz, in der Zufriedenheit mit Manager:in 1 höher ist, sind die Chancen der Ausgabevariablen Zufrieden 1,1 höher sind (10 % höher).  Wenn es sich bei der Datenzeile um eine Kategorie handelt, z.B. Farbe[blau], stellt der Koeffizient die Änderung der Chancen der Antwortvariablen dar, wenn die Kategorievariable diese bestimmte Kategorie (blau) anstelle der Baseline-Gruppe (rot, grün usw.) ist.
• Koeffizient: Jede Erhöhung von 1 Einheit in einer Eingabevariablen ist einer Erhöhung des Koeffizienten in der Ausgangsgröße zugeordnet. Diese Koeffizienten werden basierend auf den Ergebnisse der relativen Wichtigkeitsanalyse aufgebaut und passen sich daher an die Multikollinearität an und stimmen nicht mit den Koeffizienten überein, die sich aus einer standardmäßigen Ordinary Least Squares Regression ergeben würden.
• Standardisierter Koeffizient: Der standardisierte Koeffizient ist der Koeffizient geteilt durch die Varianz der Eingabevariablen. Dadurch wird jede Variable auf dieselbe Skala gesetzt, sodass ihre Koeffizienten direkter verglichen werden können.
• P-Wert: Der p-Wert ist das Maß für statistische Signifikanz. Niedrigere Werte sind mit einer geringeren Wahrscheinlichkeit verbunden, dass die Beziehung ein Zufall ist. Bei kategorischen Variablen gibt der p-Wert die statistische Signifikanz der Differenz zwischen einer Gruppe und der “Baseline”-Gruppe in der Variablen an.
• Transformieren: Siehe Variablen transformieren.

OLS-Regression analysieren

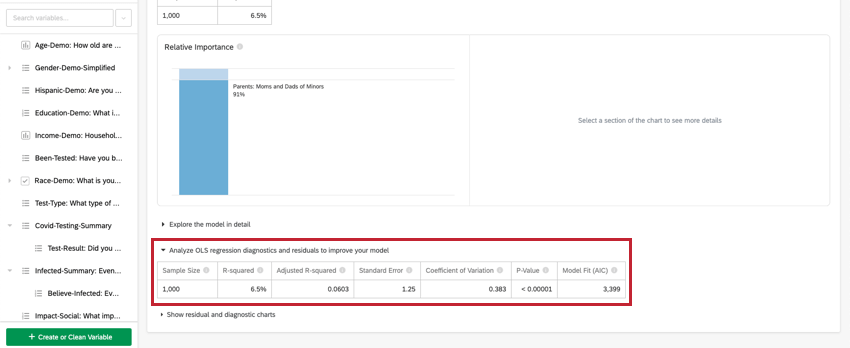
Klicken Sie für die lineare Regression auf OLS-Regressionsdiagnosen und -Residuen analysieren, um Ihr Modell zu verbessern unter der Schlüssel-/Ausgabevariable, um die Diagramme Prognostiziert vs. Ist und Residuen anzuzeigen. Siehe Interpretation von Residualdiagrammen zur Verbesserung Ihrer Regression für weitere Informationen.

Variable eingeschlossen

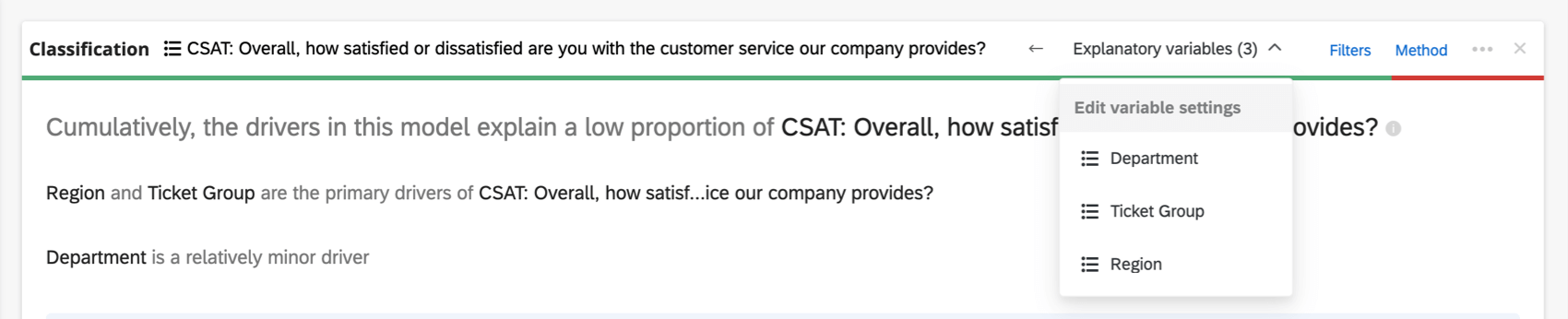
Im obersten Kopf der Regressionskarte werden die in der Regression verwendeten Variablen angezeigt.

Klicken Sie auf den Namen einer Variablen, um ein neues Fenster zu öffnen, in dem Sie umkodieren oder Bucket Werte. Klicken Sie auf die Pfeile, um zwischen den Eingabevariablen und den Ausgabevariablen in der Analyse zu wechseln.

Wenn zu viele Variablen beteiligt sind, um im Kopf angezeigt zu werden, gibt es eine Erklärende Variablen Dropdown-Liste, in der Sie zwischen den Variablen wählen können, die Sie umkodieren möchten.

Variablen hinzufügen und entfernen

Nachdem Sie eine Regressionskarte angelegt haben, können Sie der Analyse zusätzliche Variablen hinzufügen, indem Sie die folgenden Schritte ausführen:

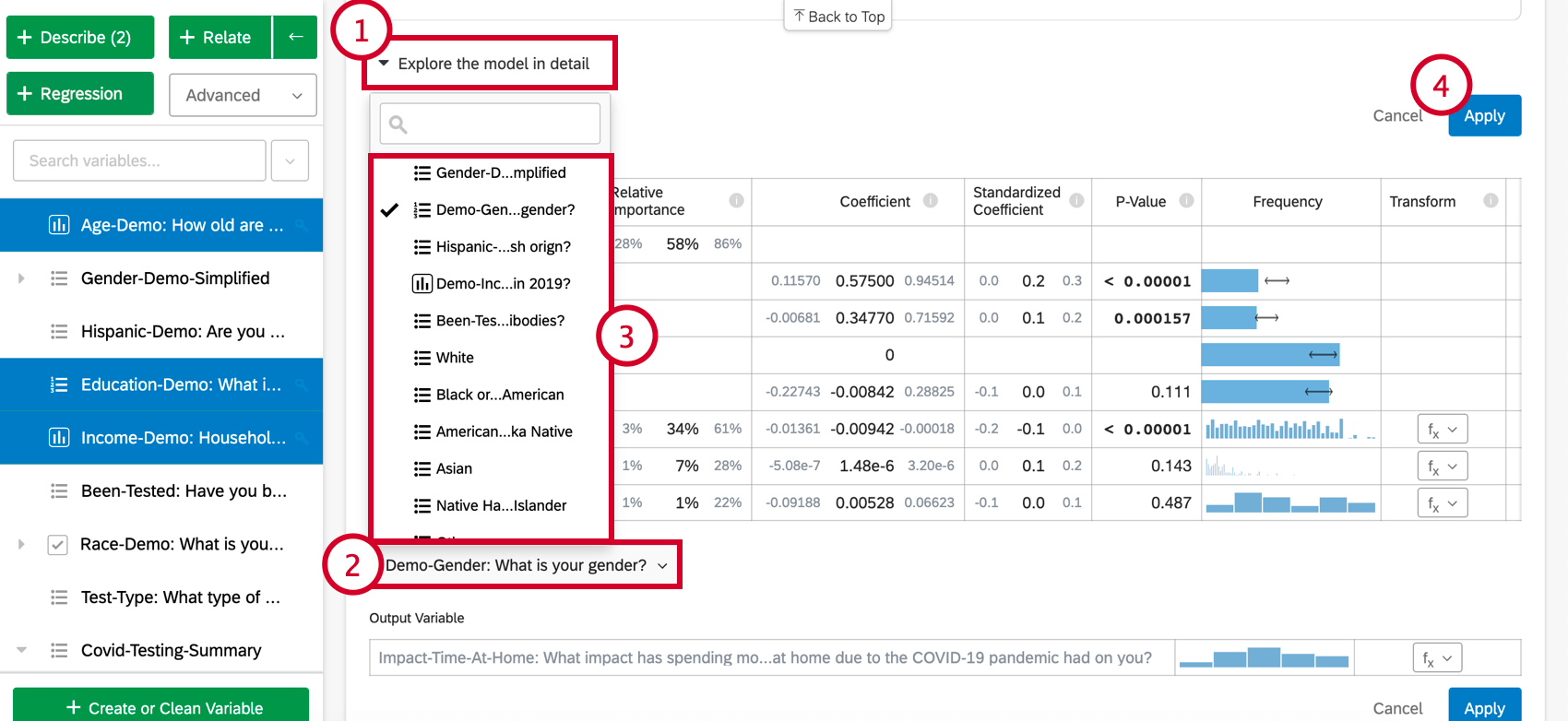
1. Klicken Sie auf Modell im Detail erkunden.
2. Auswählen Variablen zu Ihrem Modell hinzufügen unten auf der Karte. Dadurch wird eine Liste der Variablen angezeigt, die noch nicht für die Regression verwendet wurden.
3. Wählen Sie eine Variable aus dieser Liste aus.
4. Klicken Sie auf Übernehmen um die Analyse mit der neuen Variablen erneut auszuführen.

Um eine Variable aus der Regression zu entfernen, bewegen Sie den Mauszeiger über die gewünschte Variable, und klicken Sie auf das blaue X ganz rechts in der Tabelle. Nachdem Sie Variablen zum Hinzufügen oder Entfernen ausgewählt haben, stellen Sie sicher, dass Sie “Übernehmen” auswählen, um das neue Modell auszuführen.

Variablen implementieren

Die Regression berücksichtigt nur Zeilen, in denen alle Eingabevariablen Daten enthalten. Oft fehlen jedoch Daten bei der Umfrage, was sich negativ auf Ihre Regressionsanalyse und Ihr Modell auswirken kann. Wenn Sie nur Zeilen ohne fehlende Daten in Ihre Regression einbeziehen, können Ihre Ergebnisse verzerrt werden, da Ihre Stichprobe nicht für Ihr gesamtes Datenset repräsentativ ist.

Mit der Anrechnung füllt Stats iQ fehlende Daten automatisch mit geschätzten Werten. Wenn fehlende Daten eingegeben werden, können Sie mehr Ihrer ursprünglichen Daten in die Regressionsanalyse einbeziehen, was zu einem Regressionsmodell mit weniger Bias führt, das die Variation in der gewünschten Ergebnisvariablen besser erklären kann.

Die Anrechnung erfolgt automatisch. Wenn Sie also eine Regressionsanalyse für einen Datensatz mit fehlenden Werten ausführen, wird Ihr Datensatz angerechnet, bevor Berechnungen durchgeführt werden.

Klicken Sie hier, um einen Beispieldatensatz vor und nach der Anrechnung von Variablen anzuzeigen.

Vor Anrechnung:
Für diese Regression ist „Datennutzung“ die Ergebnisvariable und „Alter“, „Internetdienst“ und „Minuten der Bildzeit“ die Eingabevariablen.

Zeilen-ID	Datennutzung	Alter	Internet-Service	Bildzeit (Minuten)
1	75	39	Satellit	503
2	19	41	Faseroptik	52
3	87			434
4	54	23	Satellit
5	14			101
6	75		Satellit
7	81	57	DSL	329

Achtung: Wenn Sie eine Regression ausgeführt haben, ohne die fehlenden Werte einzugeben, werden nur die Zeilen 1, 2 und 7 berücksichtigt.

Nach Anrechnung:

Zeilen-ID	Datennutzung	Alter	Internet-Service	Bildzeit (Minuten)
1	75	39	Satellit	503
2	19	41	Faseroptik	52
3	87	50.9	FEHLT	434
4	54	23	Satellit	359.0
5	14	50,9	FEHLT	101
6	75	50,9	Satellit	359.0
7	81	57	DSL	329

Tipp: “Internet Service” ist eine kategorische Variable, keine numerische. Daher wird der fehlende Wert als “MISSING” gefüllt.

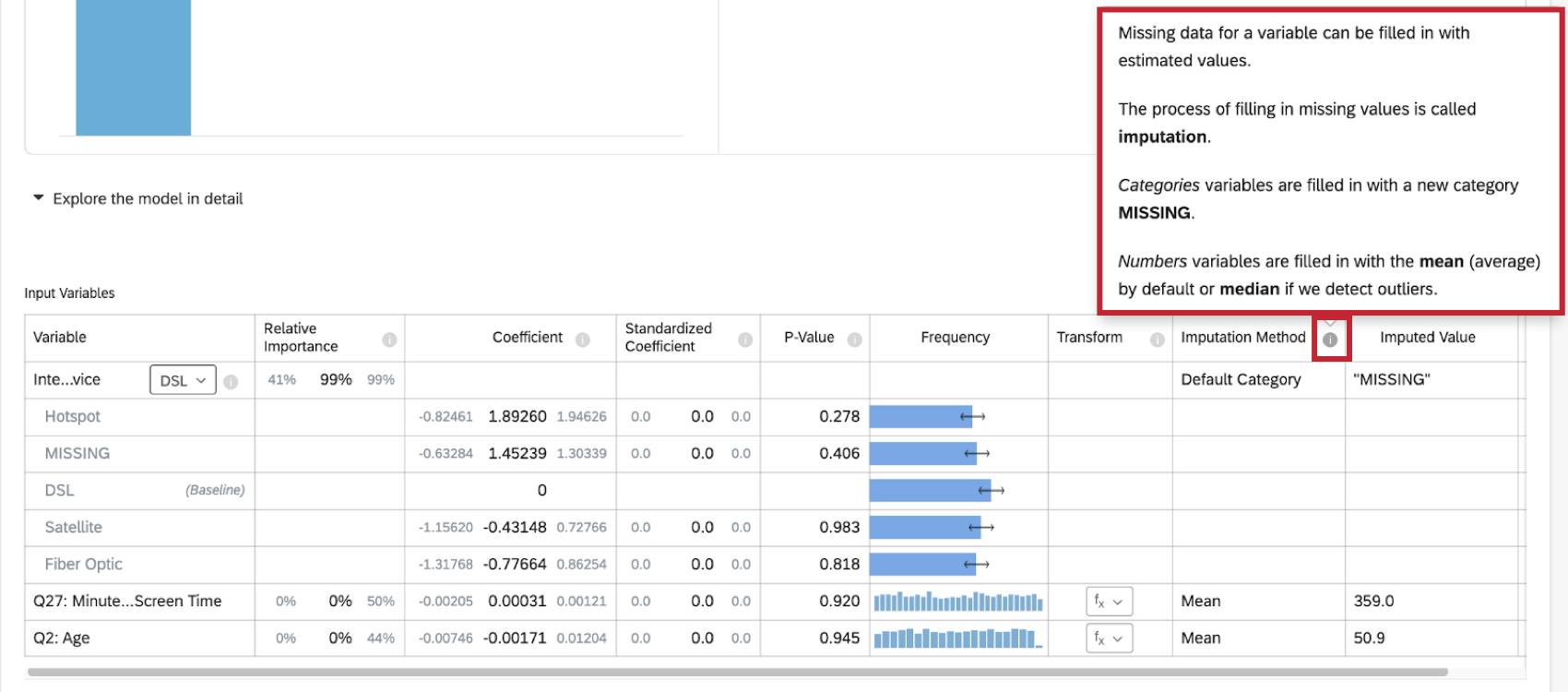
Anrechnungsmethoden

Stats iQ verwendet derzeit die folgenden Anrechnungsmethoden:

• Standardkategorie: Stats iQ erstellt einen neuen „MISSING“-Kategoriewert, um fehlende Daten einzugeben. Diese Methode wird für kategorische Variablen verwendet.
• Mittelwert: Wenn Stats iQ bei der Verteilung der numerischen Variablen keine Ausreißer erkennt, werden fehlende Daten für die Variable mit dem Mittelwert (Durchschnittswert) gefüllt. Diese Methode wird für numerische Variablen verwendet.
• Median: Wenn Stats iQ Ausreißer bei der Verteilung der numerischen Variablen erkennt, werden fehlende Daten für die Variable mit dem Median gefüllt. Diese Methode wird für numerische Variablen verwendet.

Anrechnungskennzeichen

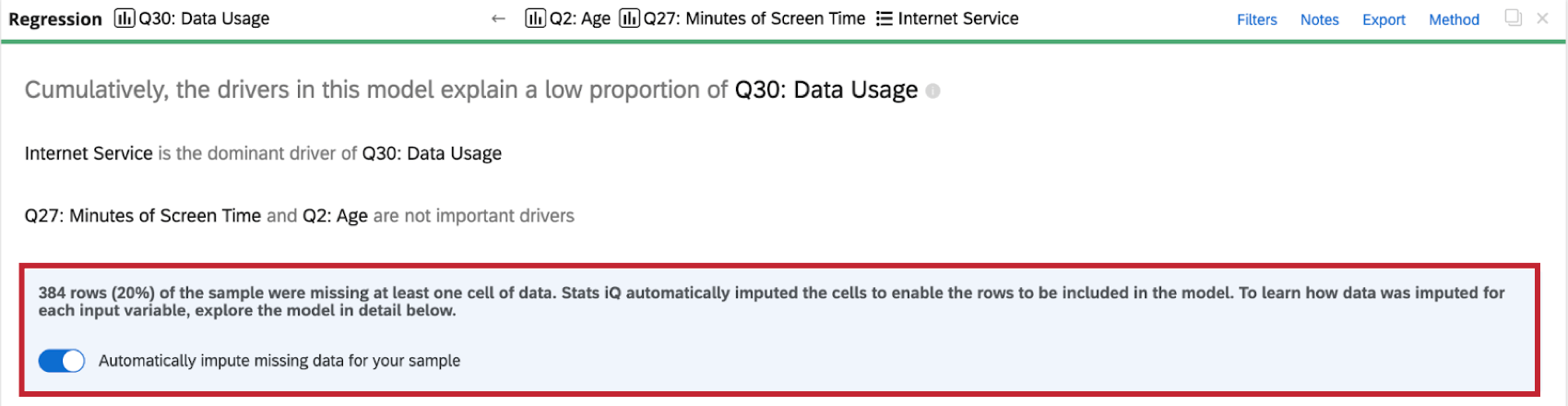
Wenn Sie eine Regressionsanalyse für den Datensatz durchführen, wird oben auf der Regressionskarte ein Anrechnungsindikator angezeigt.

Weitere Informationen zur Anrechnung erhalten Sie, wenn Sie auf das Informationssymbol ( i ) weiter Anrechnungsmethode.

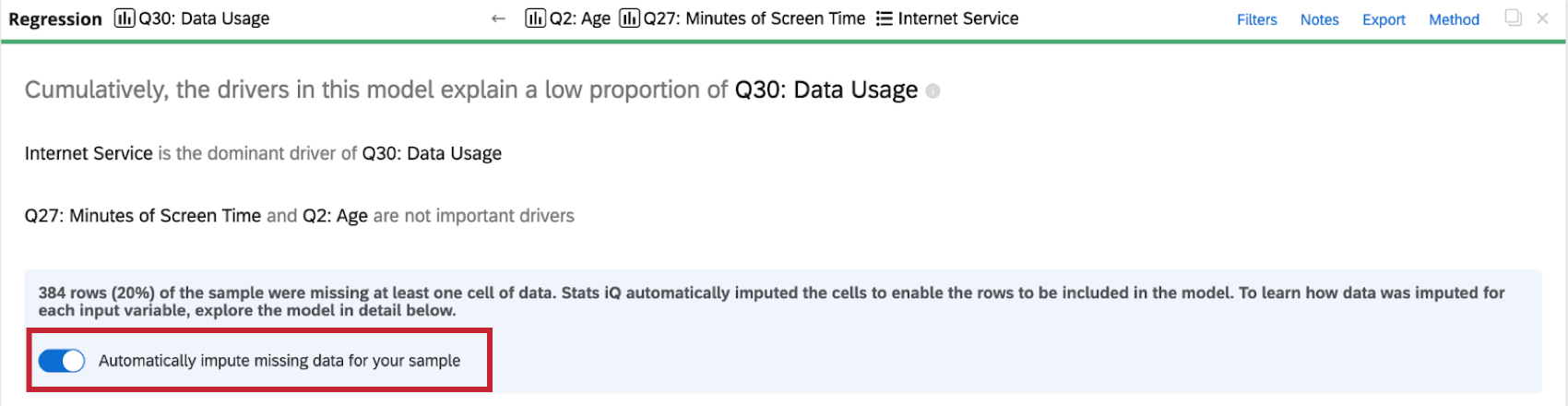
Abschalten der Anrechnung

Stats iQ wendet automatisch eine Anrechnung auf alle Regressionskarten an. Um die automatische Anrechnung zu deaktivieren, wählen Sie Fehlende Daten für Ihre Stichprobe automatisch anrechnen  oben auf der Regressionskarte.

Anrechnungswarnungen

• Wenn zu viele Daten angerechnet werden, wird Ihr Regressionsmodell voreingenommen und unzuverlässig. Wenn mehr als 50 % Ihres Datensatzes ausgefüllt wurden, warnt Stats iQ Sie, wenn Sie Schlussfolgerungen aus Ihren Ergebnisse ziehen möchten.
  
• Wenn Ausreißer in einer der numerischen Eingabevariablen erkannt werden, impliziert Stats iQ die Variablen mit dem Median anstelle des Mittelwerts. In diesem Szenario warnt Stats iQ Sie, wenn Sie das Modell im Detail untersuchen.
  

Variablen transformieren

Wenn Sie eine Regressionsanalyse in Stats iQ ausführen, stellen Sie möglicherweise fest, dass Sie Ihr Modell verbessern müssen. Die häufigste Möglichkeit, ein Modell zu verbessern, besteht darin, eine oder mehrere Variablen zu transformieren, in der Regel mithilfe eines „Protokolls“ oder einer anderen funktionalen Transformation.

Das Transformieren einer Variable ändert die Form ihrer Verteilung. Im Allgemeinen funktionieren Regressionsmodelle besser mit symmetrischen, glockenförmigen Verteilungen. Probieren Sie verschiedene Arten von Transformationen aus, bis Sie eine finden, die Ihnen diese Art der Verteilung bietet.

So transformieren Sie eine Variable:

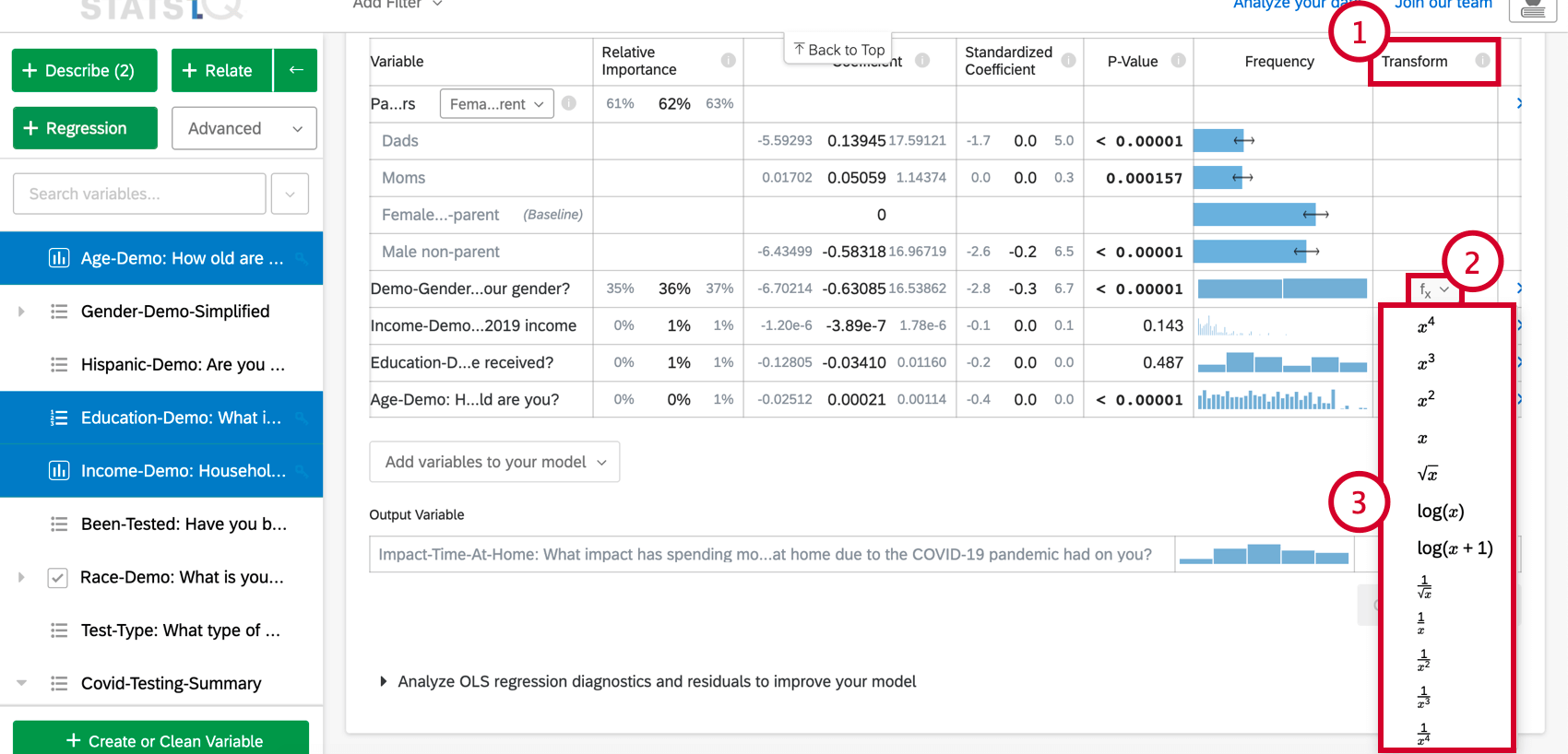
1. Unter dem Modell im Detail erkunden wählen, blättern Sie zum Transformieren Spalte.
2. Klicken Sie auf die Funktion (f(x)) für die Variable, die Sie transformieren möchten.
3. Wählen Sie aus der Liste die Funktion aus, die Sie übernehmen möchten, und Stats iQ berechnet die Karte mit der neuen transformierten Variable neu.

Die folgenden Transformationen sind in Stats iQ verfügbar:

Die bei weitem häufigste Transformation ist log(x). Sie wandelt eine „Power“-Verteilung (wie die Größe der Stadtbevölkerung) um, die viele kleinere Werte und eine kleine Anzahl größerer Werte hat, in eine glockenförmige „Verteilung“ (wie Höhe), bei der die meisten Werte in Richtung Mitte geclustert werden.

Verwenden Sie log(x+1), wenn die zu transformierende Variable einige Werte von Null hat, da log(x) nicht berechnet werden kann, wenn x gleich Null ist.

Weitere Informationen darüber, wann Sie Ihre Variablen transformieren sollten, finden Sie unter. Interpretation von Restdiagrammen zur Verbesserung Ihrer linearen Regression

Andere lineare Regressionstechniken in Stats iQ verfügbar

Die relative Wichtigkeit in Kombination mit Ordinary Least Squares ist die Standardausgabe für eine lineare Regression. Es stehen jedoch weitere Optionen zur Verfügung.

Um auf M-Schätzung, Ordinary Least Squares und Ridge Regression zuzugreifen, klicken Sie oben rechts auf Ihrer Regressionskarte auf das Zahnrad für die Einstellungen. Klicken Sie auf den Namen der Regressionstechnik unter Regressionsmethoden ermöglicht es Ihnen, die für die Regressionskarte verwendete Regressionstechnik zu ändern. Dies ist nur für die lineare Regression möglich.

• M-Schätzung: Entwickelt, um Ausreißer in der Ausgabevariablen besser zu handhaben als normale niedrigste Quadrate (OLS).
• Normalste Quadrate: Ordinary Least Squares (OLS) ist die klassische Regressionstechnik. Es ist empfindlich gegenüber Ausreißern und anderen Verstößen in seinen Annahmen, daher empfehlen wir robustere Methoden wie M-Schätzung. Da OLS in der standardmäßigen Ausgabe der relativen Wichtigkeit verwendet wird, sollten Sie diese Option nur auswählen, wenn Sie an den Funktionen interessiert sind, die noch nicht an die Ausgabe der relativen Wichtigkeit angepasst wurden: Ergebnisse prognostizieren und Interaktionsbegriffe hinzufügen.
• Ridge-Regression: Die Ridge-Regression ist eine Technik, die der OLS-Standardregression ähnelt, jedoch mit einem Alpha-Tuning-Parameter. Dieser Alpha-Parameter hilft bei der Bewältigung einer hohen Varianz und von Daten, die an Multicollinearität leiden. Bei richtiger Abstimmung liefert die Gradregression aufgrund eines besseren Kompromisses zwischen Bias und Varianz in der Regel bessere Vorhersagen als OLS. In Stats iQ können Sie den Alpha-Parameter auswählen, wenn Sie die Firge-Regression verwenden.

Sobald Sie M-Schätzung, Normale niedrigste Quadrate oder Ridge-Regression ausgewählt haben, können Sie die Ausgabe sehen. Die Ausgabe wird unter dem Regressionsmethoden Abschnitt.

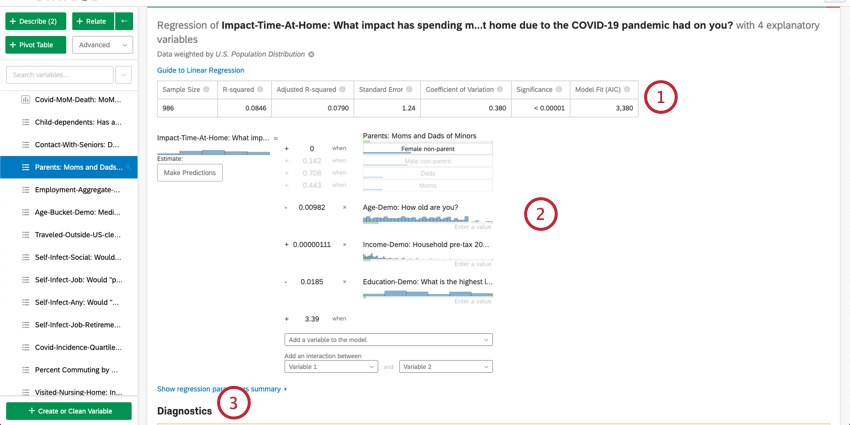
1. Numerische Zusammenfassung: Oben auf der Karte befindet sich eine Zusammenfassung für die Regressionsanalyse. Dazu gehören Stichprobe, Fehlende Fälle, Methode, R-Quadrat-Wert, Standardfehler, Variationskoeffizient und Modellanpassung.
2. Koeffizientendetails: Die primären Ergebnisse der Regression, die mathematische Gleichung, befinden sich unter der Zusammenfassung. Die Ausgabe-/Schlüsselvariable befindet sich links von der Gleichung. Die Eingabevariablen befinden sich auf der rechten Seite. Wenn Sie den Mauszeiger über eine Variable bewegen, wird eine QuickInfo angezeigt, die einfach erklärt, wie diese Variable zur Ausgabevariablen beiträgt. Hier können Sie auch Werte in die mathematische Gleichung zur Schätzung von Werten für Ihre Ausgabevariable eingeben. Weitere Informationen finden Sie im folgenden Abschnitt zum Schätzen von Ausgabevariablenwerten.
3. Diagnostik und Residuen: Stats iQ bietet Diagnosen, mit denen Sie die Genauigkeit und Gültigkeit Ihres Modells beurteilen können. mehr erfahren Sie unter Interpretation von Restdiagrammen zur Verbesserung Ihrer linearen Regression oder Die Matrix und der Precision-Recall-Tradeoff in der logistischen Regression.

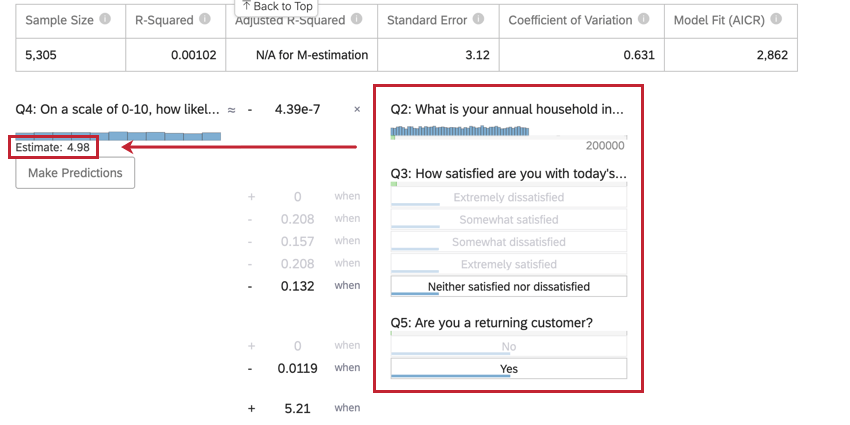
Schätzen von Ausgabevariablenwerten

Nachdem Sie eine Regression ausgeführt haben, können Sie die mathematische Gleichung im Abschnitt Koeffizientendetails verwenden, um die Werte der Ausgabevariablen basierend auf den von Ihnen ausgewählten Eingabewerten zu schätzen. Auf der rechten Seite der Gleichung sehen Sie Ihre Eingabevariablen. Sie können Werte für jede Ihrer Eingabevariablen festlegen. Auf der linken Seite der Gleichung befindet sich Ihre Ausgabevariable. Nachdem Sie Werte für Ihre Eingabevariablen eingegeben haben, berechnet die Gleichung eine Schätzung für die Ausgabevariable basierend auf dem Regressionsmodell.

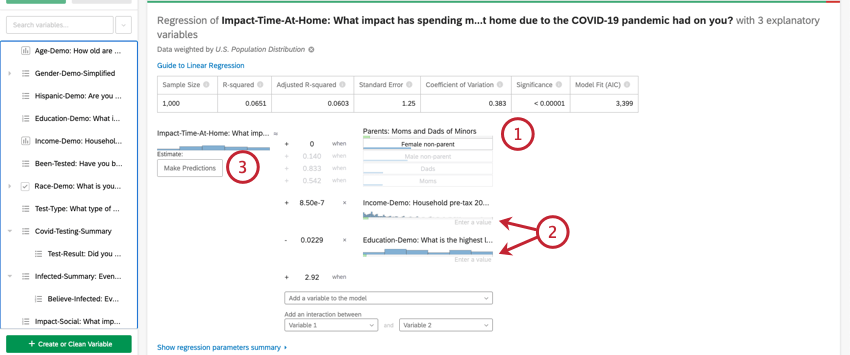
1. Diese Eingabevariablen sind ein Kategorietyp Variable. Um einen Wert für Kategorievariablen einzugeben, klicken Sie in der Liste der Optionen auf den gewünschten Wert.
2. Diese Eingabevariablen sind Nummerntyp Variablen. Um einen Wert für Zahlenvariablen einzugeben, klicken Sie auf Geben Sie einen Wert ein und geben Sie eine Zahl ein.
3. Diese Variable ist die Ausgabevariable Ihrer Regressionsgleichung. Nachdem Sie Werte für Ihre Eingabevariablen ausgewählt haben, wird weiter geschätzter Wert für Ihre Ausgabevariable angezeigt. Schätzung.

Beispiel: Im folgenden Beispiel versuchen wir, den NPS basierend auf einigen Eingabevariablen vorherzusagen. Nachdem Sie Werte für die Eingabevariablen ausgewählt haben, wird ein geschätzter NPS von 4,98 angezeigt.

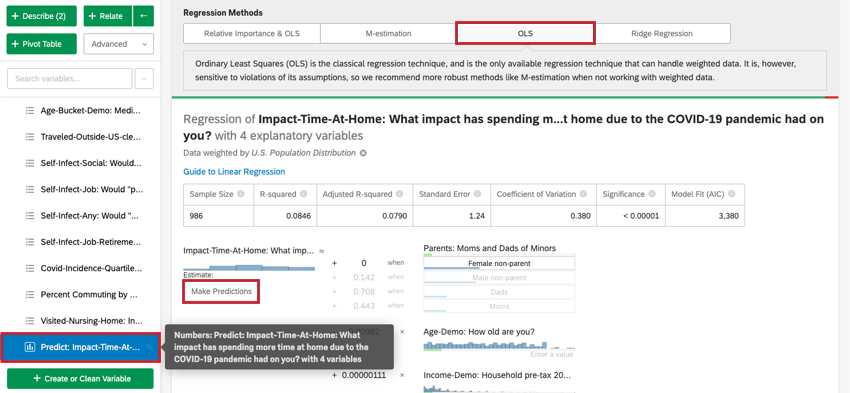
Vorhersage von Ergebnissen

In der Regel verwenden Sie die Regressionsanalyse in Stats iQ, um die Beziehung zwischen Eingabevariablen und Ausgabevariablen zu verstehen. Sobald jedoch ein Regressionsmodell angelegt wurde, kann es auch verwendet werden, um den Ausgabewert für Datenzeilen vorherzusagen, in denen Sie Werte für die Eingaben haben.

Interaktionsbedingungen und andere weiterführende Bedenken

Hinzufügen von Interaktionsbedingungen

Wenn Sie Ihr Regressionsmodell verbessern möchten, können Sie zusätzlich zu den vorhandenen Eingabevariablen Interaktionsbegriffe hinzufügen. Ein Interaktionsbegriff würde hinzugefügt, wenn Sie vermuten, dass sich der Wert einer der Eingabevariablen ändert, wie sich eine andere Eingabevariable auf die Ausgabevariable auswirkt.

Beispielsweise sind vielleicht für Menschen mit Kindern, die während eines Hotelaufenthalts anwesend sind, jüngere Menschen zufriedener als ältere Menschen, aber für Menschen ohne Kinder, die anwesend sind, sind jüngere Menschen weniger zufrieden. Das würde bedeuten, dass es eine Interaktion zwischen „Kinder präsent“ und „Alter“ gibt.

Auswahl von zwei Variablen unter Interaktion hinzufügen zwischen Am Ende der Liste der Eingabevariablen auf der Karte wird der Regression ein Interaktionsbegriff hinzugefügt. Diese Funktion ist nur in Ordinary Least Squares, M-Estimation und Ridge Regression verfügbar.

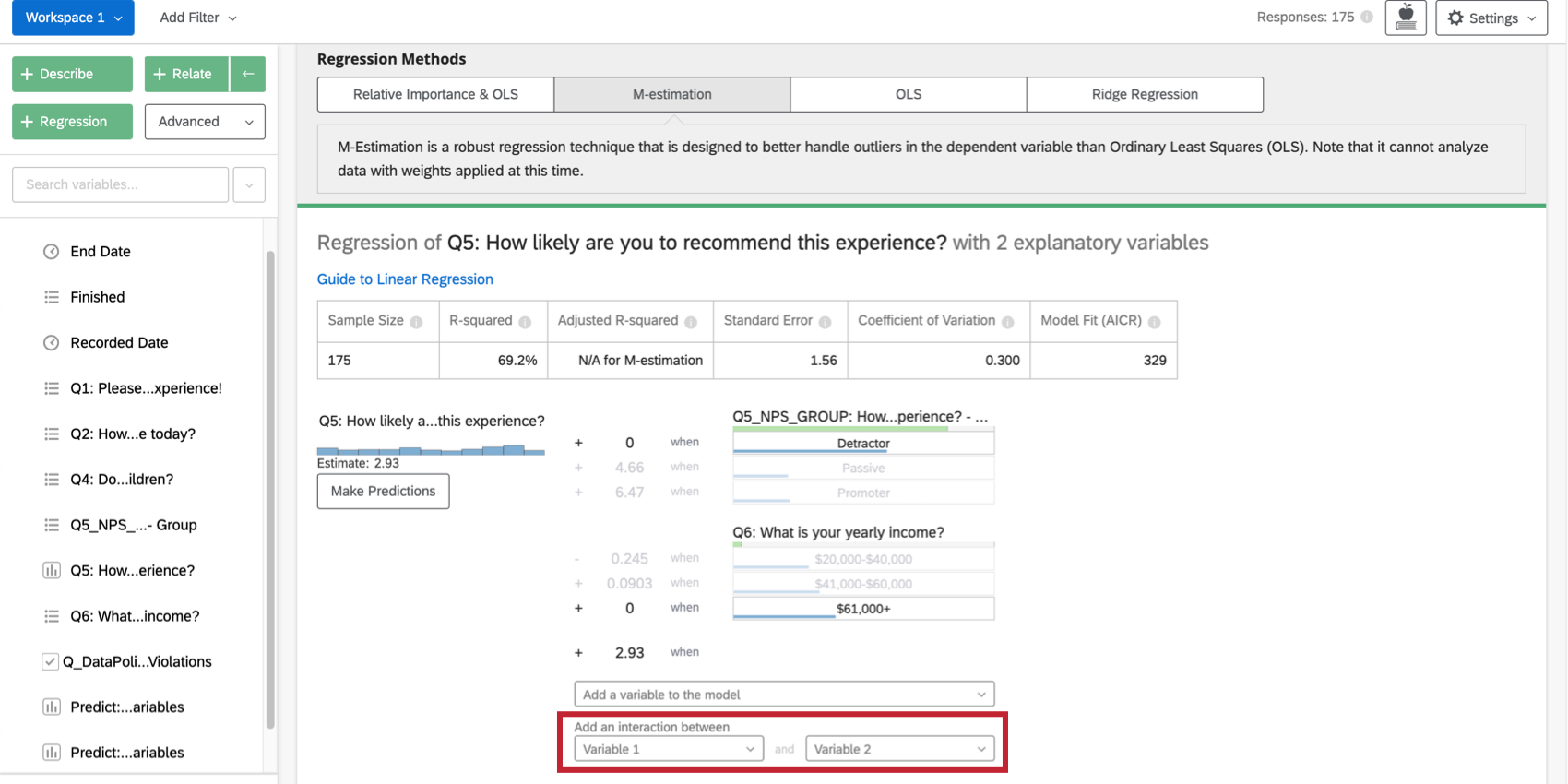
Sie können denselben Effekt für kategorische Variablen in einer relativen Wichtigkeitsanalyse erzielen, indem Sie Erstellen einer neuen Variablen die beides kombiniert. Sie können beispielsweise die Variable Farbe (mit rot und grün Gruppen) mit Größe (mit groß und klein Gruppen), um eine Variable mit dem Namen Farbgröße (mit Gruppen BigRed, BigGreen, SmallRed, und SmallGreen).

Multicollinearity

Mehrfarbigkeit tritt in einem Regressionskontext auf, wenn zwei oder mehr der Eingabevariablen stark miteinander korrelieren.

Wenn zwei Variablen stark korreliert sind, stellt die Mathematik für die Regression in der Regel so viel Wert wie möglich in eine Variable und nicht in die andere. Dies manifestiert sich in einem größeren Koeffizienten für diese Variable. Wenn das Modell jedoch auch einen kleinen Betrag ändert (z.B. durch Hinzufügen eines Filters), kann sich die Variable ändern, in der der größte Teil des Werts platziert wurde. Das bedeutet, dass auch eine kleine Änderung eine drastische Auswirkung auf das Regressionsmodell haben kann.

Die Analyse der relativen Wichtigkeit behandelt dieses Problem, sodass Sie sich keine Sorgen darum machen müssen. Wenn Sie eine der anderen Methoden verwenden möchten und Ihr Modell dieses Problem aufweist, löst das Vorhandensein von Mehrfarblinearität (gemessen durch “Varianzinflationsfaktor”) eine Warnung Auslöser und schlägt vor, dass Sie eine Variable entfernen oder Variablen kombinieren, indem Sie sie z.B. im Durchschnitt vergleichen.

Warnmeldungen

Stats iQ warnt Sie, wenn es potenzielle Probleme mit Ihren Ergebnisse gibt. Dazu gehören folgende Situationen:

• Eingabevariablen in Ihrer Regression sind nicht statistisch signifikant.
• Ihre Transformation hat Daten aus der Regression entfernt.
• Zwei oder mehr Variablen sind stark miteinander korreliert und machen Ihre Ergebnisse instabil, d.h. Multicollinearity.
• Die Reste haben ein Muster, das darauf hinweist, dass das Modell verbessert werden könnte.
• Eine Variable mit nur einem Wert wurde automatisch entfernt.
• Die Stichprobe ist im Verhältnis zur Anzahl der Eingabevariablen in der Regression zu niedrig.
• Eine Kategorievariable mit zu vielen Antwortoptionen wurde hinzugefügt.

FAQs