Benutzerfreundlicher Leitfaden zur logistischen Regression

Was ist logistische Regression?

Die logistische Regression schätzt eine mathematische Formel, die eine oder mehrere Eingabevariablen mit einer Ausgabevariablen in Beziehung setzt.

Angenommen, Sie führen einen Limonadenstand und sind daran interessiert, welche Arten von Kunden eher zurückkommen. Ihre Daten umfassen einen Eintrag für jeden Kunden, seinen ersten Kauf und ob er im nächsten Monat für mehr Limonade zurückgekehrt ist. Ihre Daten könnten wie folgt aussehen:

Sie sind der Meinung, dass “Alter des Kunden” (eine Eingabe- oder erklärende Variable) Auswirkungen auf “Return” (eine Ausgabe- oder Antwortvariable) haben könnte. Logistische Regression kann zu diesem Ergebnis führen:

Im Alter von 12 Jahren (das niedrigste Alter) beträgt die Wahrscheinlichkeit, dass die Rückkehr “zurückgegeben” wird, 10 %.

Für jedes zusätzliche Lebensjahr ist „Rückkehr“ 1,1-mal mehr, um „zurückgegeben“ zu werden.

Dieses Wissen ist aus zwei Gründen nützlich.

Erstens können Sie damit eine Beziehung verstehen: Ältere Kunden werden häufiger zurückkehren. Diese Erkenntnisse könnten Sie dazu veranlassen, Ihre Werbung älteren Kunden anzubieten, da sie häufiger zu Wiederkunden werden.

Zweitens und zeitnah kann es Ihnen auch dabei helfen, bestimmte Prognosen zu erstellen. Wenn ein 24-jähriger Kunde vorbeikommt, könnten Sie davon ausgehen, dass er, wenn er Limonade kauft, eine Wahrscheinlichkeit von 26 % hat, dass er später ein Retourenkunde wird.

Verstehen der Multiplikation von Chancen

Beachten Sie, dass wir, wenn wir sagten, “Zurückgegeben” sei “1,5 mal wahrscheinlicher” in einer Situation als in einer anderen, tun wir die folgenden:

Quoten waren 1:9, auch geschrieben 1/(1+9) = 10%.

Die „Chancen für“ (die 1) werden mit 1,5 multipliziert.

Jetzt 1,5:9, auch geschrieben 1,5/(1,5+9) = 14%.

Ein weiteres Beispiel, dieses Mal, um von 50% Wahrscheinlichkeit zu etwas 3 Mal als wahrscheinlich zu gehen:

Quoten waren 1:1, auch geschrieben 1/(1+1) = 50%.

Die “Chancen für” (linke Seite 1) werden mit 3 multipliziert.

Nun 3:1, auch geschrieben 3/(3+1) = 75%.

Nun gehen wir durch den Prozess zum Erstellen dieses Regressionsmodells.

Erstellen eines Regressionsmodells vorbereiten

1. Denken Sie an die Theorie Ihrer Regression.

Nachdem Sie eine Antwortvariable ausgewählt haben, hypothetisieren “Umsatz“, wie verschiedene Eingaben damit zusammenhängen können. Sie könnten beispielsweise glauben, dass eine höhere “Temperatur beim ersten Kauf” zu einer höheren Wahrscheinlichkeit von “Zurückgegeben” führt. Sie sind sich möglicherweise nicht sicher, wie “Alter” sich auf “Rückkehr” auswirkt, und Sie könnten glauben, dass “Hosen” (im Gegensatz zu Shorts) von “Temperatur” betroffen sind, sich aber nicht auf Ihren Limonadenstand auswirken.

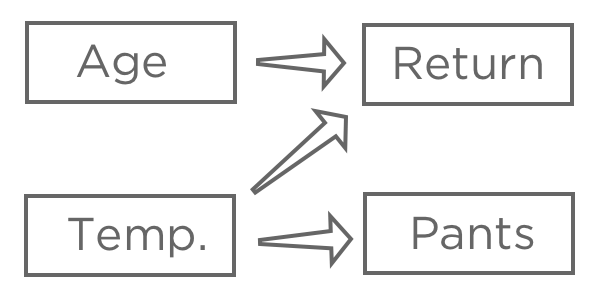
Das Ziel der Regression besteht in der Regel darin, die Beziehung zwischen mehreren Eingaben und einer Ausgabe zu verstehen. Daher würden Sie in diesem Fall wahrscheinlich ein Modell erstellen, das “Rückgabe” mit “Temperatur” und “Alter” erklärt (auch als “Rückkehr von Temperatur und Alter vorhersagen” gesagt, auch wenn Sie mehr an einer Erklärung als an der tatsächlichen Vorhersage interessiert sind).

Wahrscheinlich würden Sie “Hosen” nicht in Ihre Regression einbeziehen. Es kann mit “Return” korreliert werden, da beide mit “Temperatur” verknüpft sind, aber nicht vor “Return” in der Kausalkette stehen, sodass es Ihr Modell verwirren würde.

2. Beschreiben Sie alle Variablen, die für Ihr Modell nützlich sein könnten.

Beginnen Sie mit der Beschreibung der Antwortvariablen, in diesem Fall “Umsatz”, und erhalten Sie ein gutes Gefühl dafür. Wiederholen Sie diese Schritte für Ihre erklärenden Variablen.

Hinweis, die eine solche Form haben…

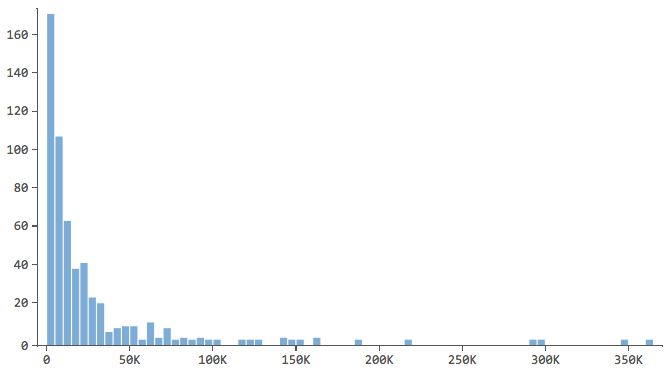
…wobei sich der Großteil der Daten in den ersten Bins des Histogramms befindet. Diese Variablen erfordern später besondere Aufmerksamkeit.

3. „Verknüpfen“ Sie alle möglichen erklärenden Variablen mit der Response-Variable.

Stats iQ sortiert die Ergebnisse nach der Stärke der statistischen Beziehung. Schauen Sie sich die Ergebnisse an, und notieren Sie, welche Variablen sich auf „Umsatz“ beziehen und wie.

4. Beginnen Sie mit dem Aufbau der Regression.

Die Erstellung eines Regressionsmodells ist ein iterativer Prozess. Sie durchlaufen die folgenden drei Phasen so oft wie nötig.

Die drei Stufen des Aufbaus eines Regressionsmodells

Stufe 1: Addieren oder Subtrahieren einer Variablen.

Beginnen Sie nacheinander, Variablen hinzuzufügen, die Ihre vorherigen Analysen auf “Umsatz” bezogen haben (oder fügen Sie Variablen hinzu, für die Sie einen theoretischen Grund haben). Es ist nicht unbedingt notwendig, nacheinander zu gehen, aber es erleichtert Ihnen, Probleme im Laufe der Zeit zu erkennen und zu beheben, und hilft Ihnen, ein Gefühl für das Modell zu bekommen.

Angenommen, Sie sagen zunächst „Umsatz“ mit „Temperatur“ voraus. Sie finden eine starke Beziehung, bewerten das Modell und finden es zufriedenstellend (weitere Details in einer Minute).

Return <– TemperatureSie

fügen dann “Lemonade color” hinzu und jetzt hat Ihr Regressionsmodell zwei Begriffe, die beide statistisch signifikante Prädiktoren sind. So:

Umsatz <– Temperatur & LimonadefarbDann

fügen Sie “Sex” hinzu, und die Modellergebnisse zeigen nun, dass “Sex” statistisch signifikant im Modell ist, aber “Limonadefarbe” nicht mehr. In der Regel entfernen Sie “Limonadenfarbe” aus dem Modell. Jetzt haben wir:

Umsatz <– Temperatur & SexDas

ist, wenn Sie das Geschlecht des Kunden kennen, wenn Sie wissen, welche Farbe von Limonade sie bestellt haben, gibt Ihnen keine weiteren Informationen darüber, ob es sich um einen Retourenkunden handelt.

Sie könnten untersuchen und feststellen, dass Frauen dazu neigen, gelbe Limonade mehr zu wählen als Männer und dass Frauen häufiger zurückkehren. Daher schien es zunächst so, als ob die Wahl von Gelb dazu führte, dass ein Kunde eher zurückkehren würde, aber tatsächlich steht “Limonadenfarbe” nur in Zusammenhang mit “Return” durch “Sex“. Wenn Sie also “Sex” in die Regression aufnehmen, wird “Lemonade color” aus der Regression entfernt.

Das Interpretieren von Regressionsergebnissen erfordert eine hohe Ermessensausübungen, und nur weil eine Variable statistisch signifikant ist, bedeutet dies nicht, dass sie tatsächlich kausal ist. Wenn Sie jedoch Variablen sorgfältig hinzufügen und subtrahieren, sich merken, wie sich das Modell ändert, und immer über die Theorie hinter Ihrem Modell nachdenken, können Sie interessante Beziehungen in Ihren Daten auseinanderhalten.

Phase 2: Bewerten Sie das Modell.

Jedes Mal, wenn Sie eine Variable hinzufügen oder subtrahieren, sollten Sie die Genauigkeit des Modells bewerten, indem Sie das R-Quadrat (^R2), AICc und alle Warnungen von Stats iQ betrachten. Vergleichen Sie jedes Mal, wenn Sie das Modell ändern, die neuen R-Quadrat-, AICC- und Diagnosediagramme mit den alten, um zu ermitteln, ob sich das Modell verbessert hat oder nicht.

R-Quadrat (^R2)

Die numerische Kennzahl zur Quantifizierung der Prognosegenauigkeit des Modells wird als R-Quadrat bezeichnet und liegt zwischen Null und Eins. Eine Null bedeutet, dass das Modell keinen Prognosewert hat, und ein Wert, der bedeutet, dass das Modell alles perfekt vorhersagt.

Beispielsweise führen die links dargestellten Daten zu einem wesentlich ungenaueren Modell als die Daten auf der rechten Seite. Stellen Sie sich vor, Sie würden versuchen, eine Linie durch das Streudiagramm zu ziehen. Sie könnten Blau („Zurückgegeben“) fast vollständig von Rot („Nicht gefunden“) auf der rechten Seite trennen, aber auf der linken Seite wäre es schwierig, dies zu tun.

Das heißt, die rechte Seite hat ein hohes R-Quadrat; wenn man “Temperatur” und “Alter” kennt, kann man “Zurückgegeben” vs. “War nicht” ganz einfach. Die linke Seite hat ein wenig zu mittleres R-Quadrat; wenn man “Temperatur” und “Alter” kennt, hat man eine ziemlich gute Vermutung, ob es “zurückgegeben” wird vs. “Nicht”, aber es wird viele Fehler geben.

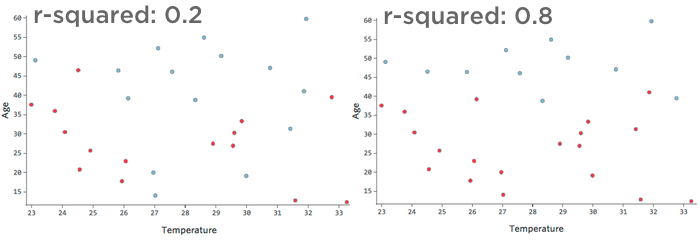
Es gibt keine feste Definition eines „guten“ R-Quadrats. In einigen Einstellungen kann es interessant sein, irgendwelche Auswirkungen zu sehen, während in anderen Einstellungen Ihr Modell nutzlos sein könnte, es sei denn, es ist sehr genau.

Jedes Mal, wenn Sie eine Variable hinzufügen, steigt das R-Quadrat, sodass das Erreichen des höchstmöglichen R-Quadrats nicht das Ziel ist. Stattdessen möchten Sie die Genauigkeit des Modells (R-Quadrat) mit seiner Komplexität (in der Regel die Anzahl der darin enthaltenen Variablen) ausgleichen.

AICc

AICc ist eine Kennzahl, die die Genauigkeit mit der Komplexität in Einklang bringt. Eine höhere Genauigkeit führt zu besseren Scores, und zusätzliche Komplexität (mehr Variablen) führt zu schlechteren Scores. Das Modell mit dem unteren AICc ist besser.

Beachten Sie, dass die AICc-Metrik nur für den Vergleich von AICcs aus Modellen nützlich ist, die dieselbe Anzahl von Datenzeilen und dieselbe Ausgabevariable haben.

Warnungen

Von Zeit zu Zeit schlägt Stats iQ Möglichkeiten zur Verbesserung Ihres Modells vor. Beispielsweise kann Stats iQ vorschlagen, den Logarithmus einer Variablen zu verwenden (Details dazu, was das bedeutet).

Verwechslungsmatrix und Präzisionsrückrufkurve

Die Verwechslungsmatrix und die Precision-Recall-Kurve sind auch nützliche Werkzeuge, um zu verstehen, wie genau Ihr Modell ist. Und wenn Sie Prognosen basierend auf Ihrem Modell erstellen möchten, helfen Ihnen diese Tools dabei. Sie sind nicht unbedingt erforderlich, um ein gutes Verständnis dafür zu erhalten, was Ihr Modell Ihnen sagt. Daher stellen wir sie in einen anderen Abschnitt über die Verwechslungsmatrix und die Präzisionsrückruf-Kurve
.

Stufe 3: Passen Sie das Modell entsprechend an.

Wenn Ihre Bewertung des Modells zufriedenstellend war, sind Sie entweder fertig, oder Sie können zu Stufe 1 zurückkehren und weitere Variablen eingeben.

Wenn Ihre Bewertung feststellt, dass das Modell fehlt, verwenden Sie Stats iQ’s Alerts, um die Probleme zu beheben.

Wenn Sie das Modell ändern, beachten Sie kontinuierlich die wechselnde R-Quadrat-, AICR- und Residualdiagnostik, und entscheiden Sie, ob die Änderungen, die Sie vornehmen, Ihr Modell unterstützen oder schädigen.

Häufig gestellte Fragen