Restplots interpretieren, um Ihre Regression zu verbessern
Wenn Sie eine Regression ausführen, berechnet und zeichnet Stats iQ automatisch Residuen, damit Sie Ihr Regressionsmodell besser verstehen und verbessern können. Lesen Sie unten alles, was Sie über die Interpretation von Residuen (einschließlich Definitionen und Beispiele) wissen müssen.
Beobachtungen, Prognosen und Residuen
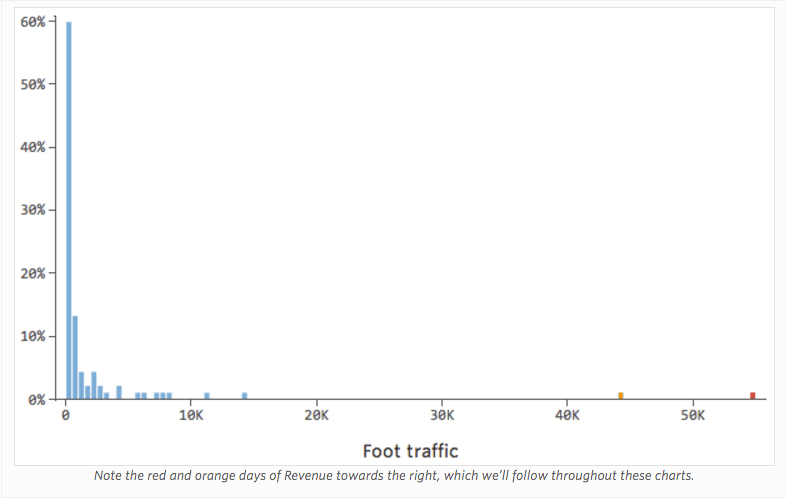
Um die Interpretation von Residuen zu demonstrieren, verwenden wir einen Limonadenstandsdatensatz, bei dem jede Zeile einen Tag mit „Temperatur“ und „Umsatz“ war.
| Temperatur (Celsius) | Umsatz |
|---|---|
| 28,2 | 44 USD |
| 21,4 | 23 EUR |
| 32,9 | 43 USD |
| 24,0 | 30 EUR |
| usw. | usw. |
Die Regressionsgleichung, die die Beziehung zwischen „Temperatur und “Umsatz” beschreibt, ist:
Umsatz = 2,7 * Temperatur – 35Nehmen wir
an, ein Tag am Limonadestand waren es 30,7 Grad und “Umsatz” betrug 50 $. 50 ist Ihre beobachtete oder tatsächliche Ausgabe, also der Wert, der tatsächlich aufgetreten ist.
Wenn wir also 30,7 bei unserem Wert für „Temperatur“ einfügen …
Umsatz = 2,7 * 30,7 – 35
Umsatz = 48
… erhalten wir 48 USD. Dies ist der prognostizierte Wert für diesen Tag, auch bekannt als der Wert für „Umsatz“, den die Regressionsgleichung basierend auf der „Temperatur“ prognostiziert hätte.
Ihr Modell ist natürlich nicht immer perfekt richtig. In diesem Fall ist die Vorhersage um 2 abzüglich; diese Differenz, die 2, wird als Restwert bezeichnet. Der Restwert ist der Teil, das übrig bleibt, wenn Sie den prognostizierten Wert vom Beobachtungswert subtrahieren.
Restwert = Beobachtet – Vorhergesagt
Sie können sich vorstellen, dass jede Datenzeile nun zusätzlich einen prognostizierten Wert und einen Restwert aufweist.
| Temperatur (Celsius) |
Umsatz (beobachtet) |
Umsatz (prognostiziert) |
Restwert (beobachtet – prognostiziert) |
|---|---|---|---|
| 28,2 | 44 USD | 41 USD | 3 EUR |
| 21,4 | 23 EUR | 23 EUR | 0 EUR |
| 32,9 | 43 USD | 54 USD | – 11 USD |
| 24,0 | 30 EUR | 29 EUR | 1 USD |
| usw. | usw. | usw. | usw. |
Wir werden die beobachteten, prognostizierten und Restwerte verwenden, um das Modell zu bewerten und zu verbessern.
Genauigkeit mit beobachtetem vs. Vorhergesagt
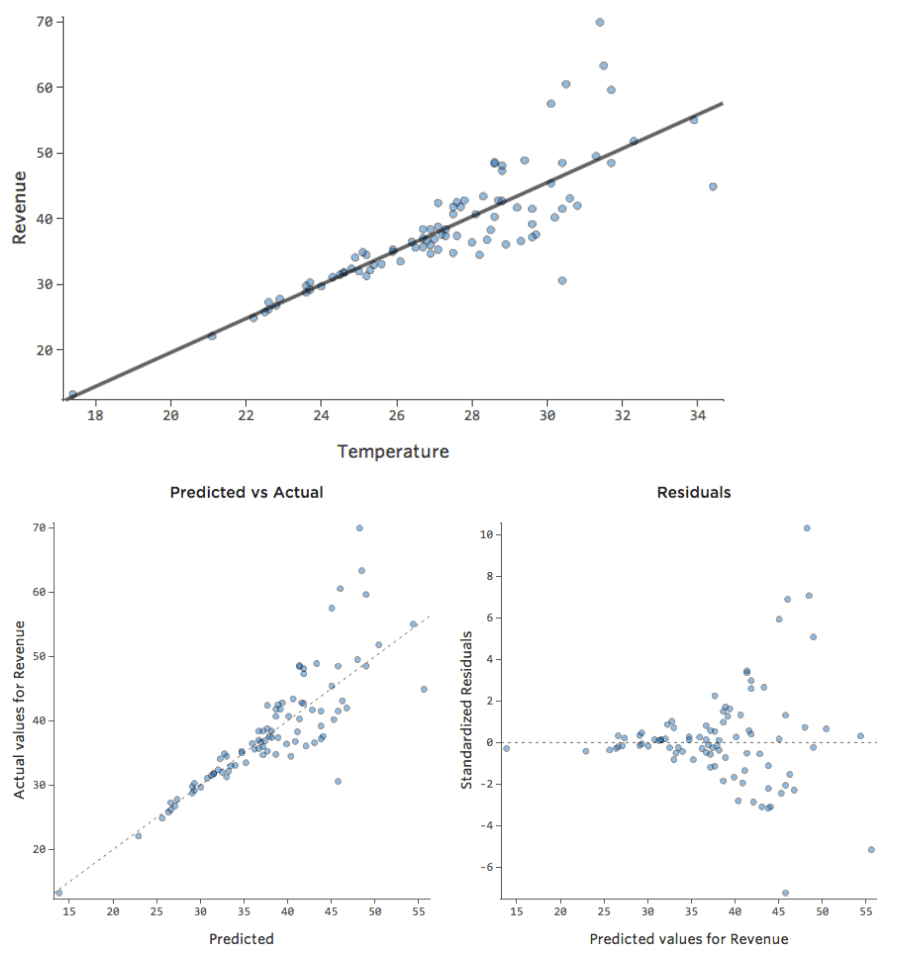
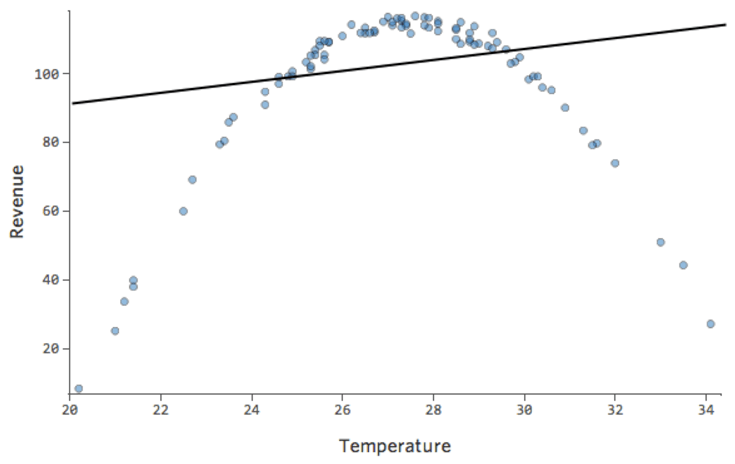
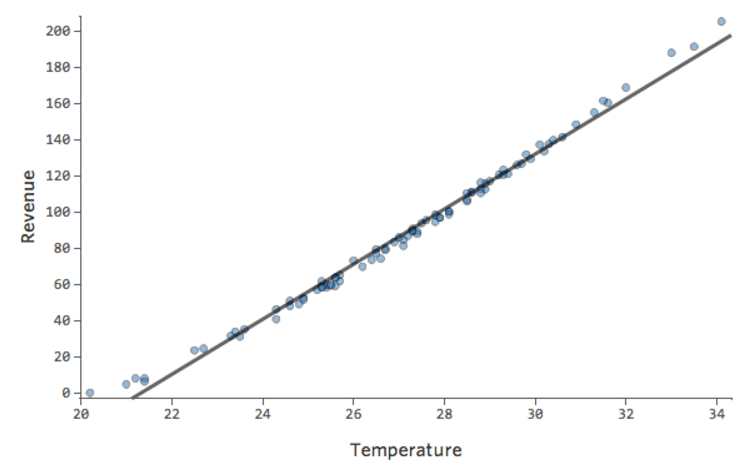
In einem einfachen Modell wie diesem, mit nur zwei Variablen, können Sie erkennen, wie genau das Modell ist, indem Sie „Temperatur“ mit „Umsatz“ verknüpfen. Hier ist der gleiche Regressionslauf auf zwei verschiedenen Limonadenständen, eine, bei der das Modell sehr genau ist, eine, bei der das Modell nicht:
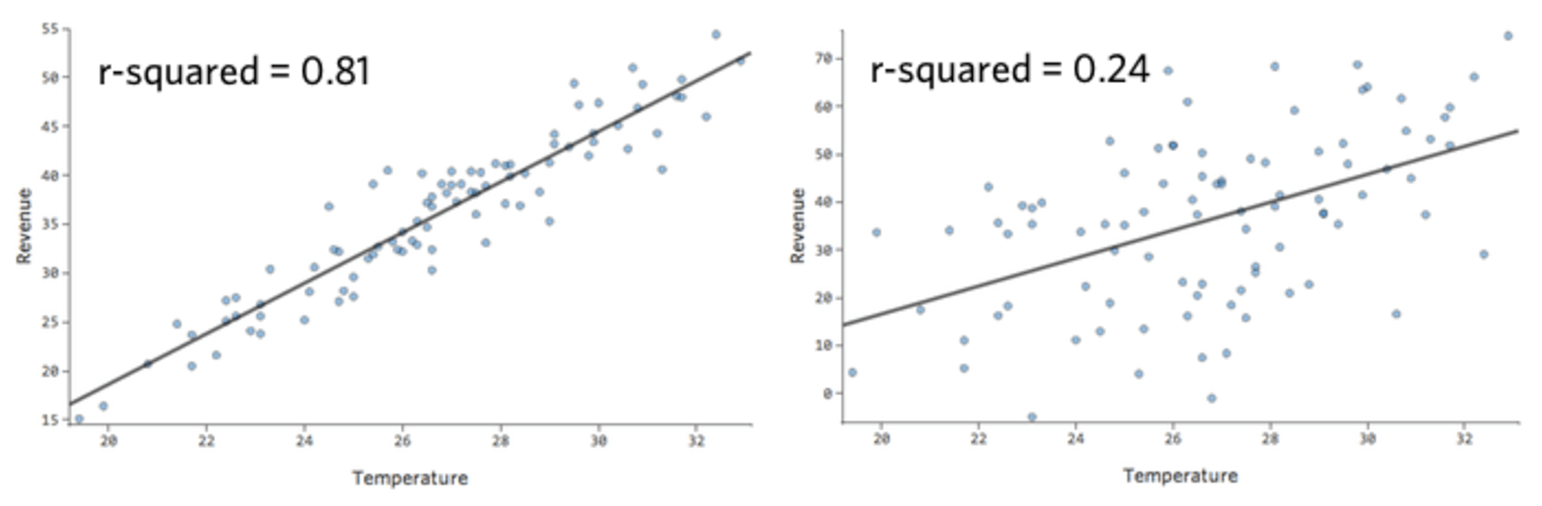
Klar ist, dass für beide Limonadenstände eine höhere „Temperatur“ mit höherem „Umsatz“ verbunden ist. Aber bei einer gegebenen „Temperatur“ könnte man den „Umsatz“ der linken Limonade viel genauer prognostizieren als der rechte Limonadenstand, was bedeutet, dass das Modell viel genauer ist.
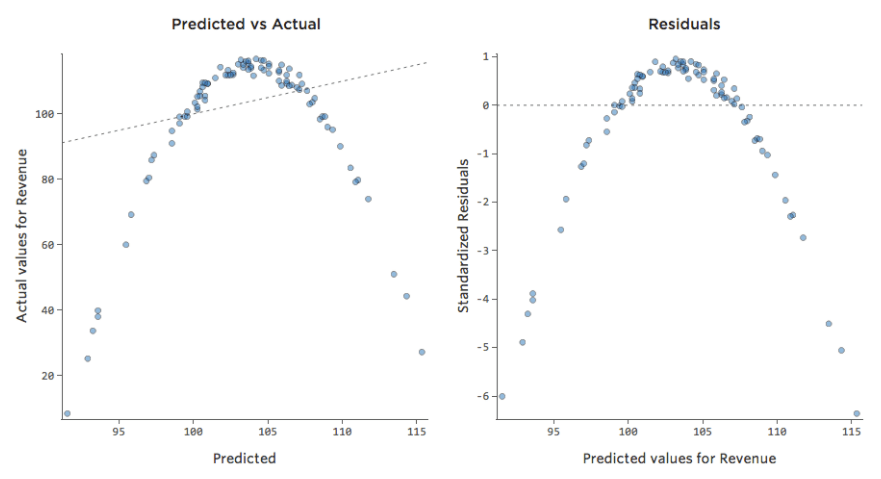
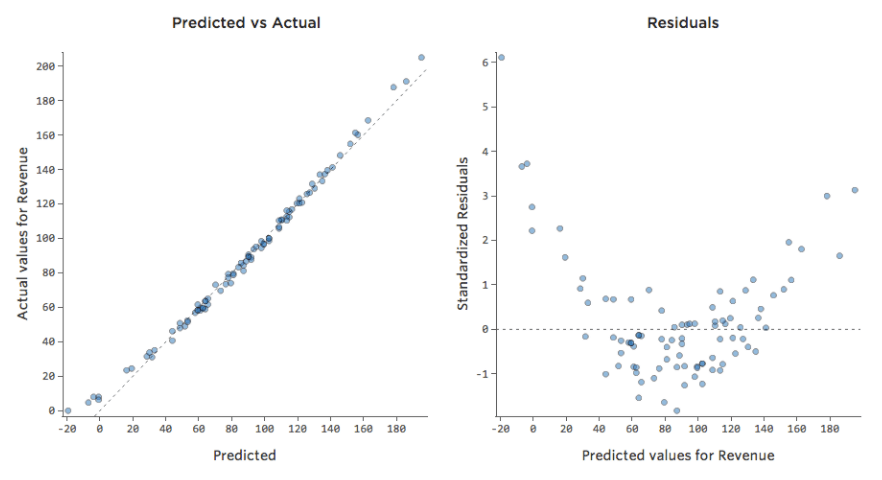
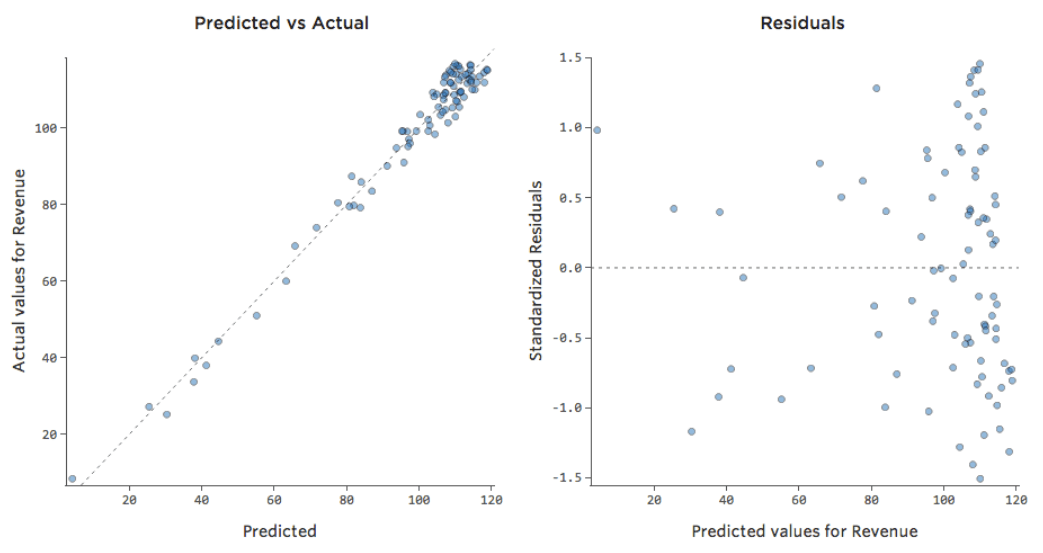
Die meisten Modelle haben jedoch mehr als eine erklärende Variable, und es ist nicht praktikabel, mehr Variablen in einem solchen Diagramm darzustellen. Lassen Sie uns also die prognostizierten Werte im Vergleich zu den beobachteten Werten für diese gleichen Datensets darstellen.
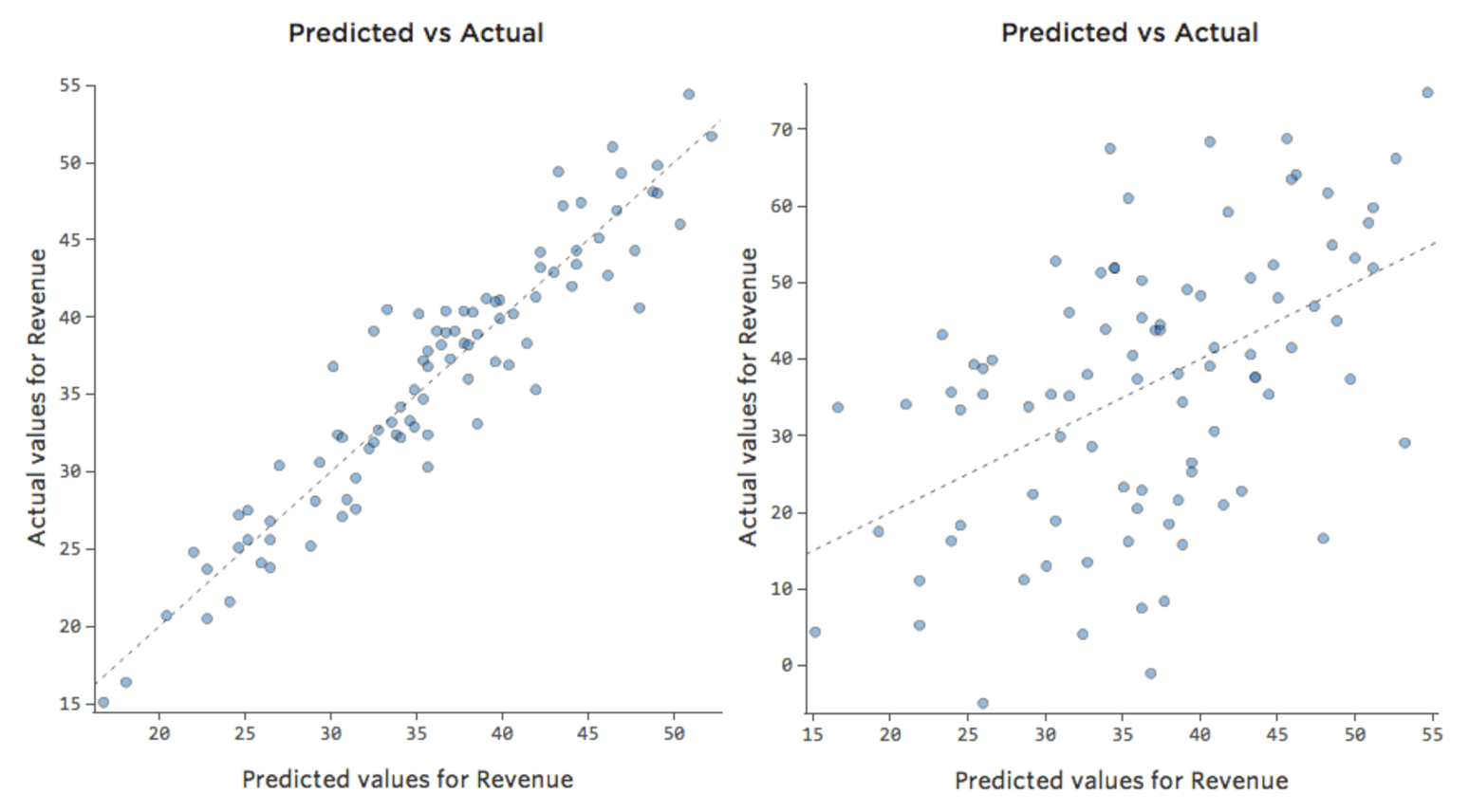
Auch hier ist das Modell für das Diagramm auf der linken Seite sehr genau. Es besteht eine starke Korrelation zwischen den Prognosen des Modells und seinen tatsächlichen Ergebnissen. Das Modell für das Diagramm ganz rechts ist das Gegenteil; die Vorhersagen des Modells sind überhaupt nicht sehr gut.
Beachten Sie, dass diese Diagramme genauso aussehen wie „Temperatur“ vs. „Umsatz“-Diagramme darüber, aber auf der X-Achse wird „Umsatz“ anstelle von „Temperatur“ prognostiziert. Das ist üblich, wenn Ihre Regressionsgleichung nur eine erklärende Variable hat. Häufiger haben Sie jedoch mehrere erklärende Variablen, und diese Diagramme sehen ganz anders aus als ein Diagramm einer beliebigen erklärenden Variablen im Vergleich zu. „Umsatz.“
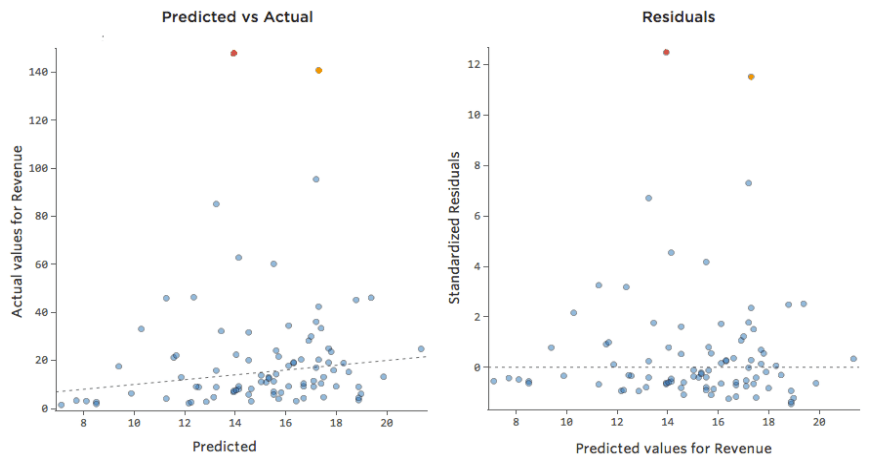
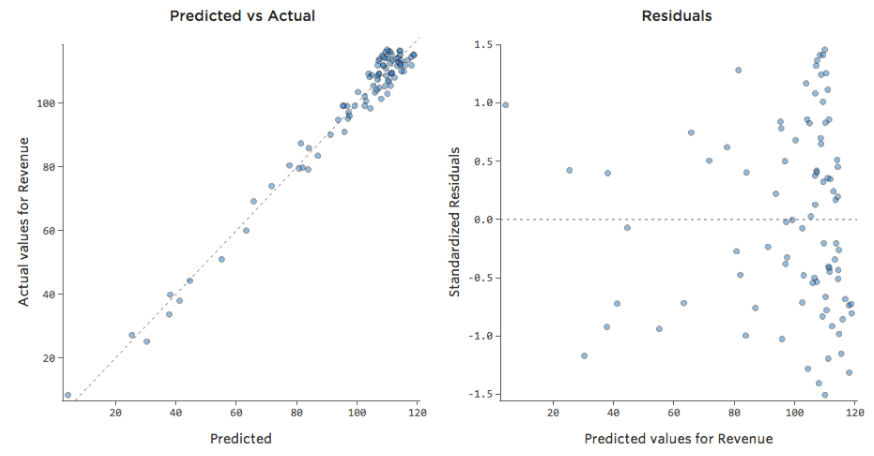
Prognostizierte vs. Residual („The Residual Plot“)
Die sinnvollste Methode zum Zeichnen der Residuen ist jedoch die Darstellung mit Ihren Prognosewerten auf der X-Achse und Ihren Residuen auf der Y-Achse.
(Stats iQ stellt Residuen als standardisierte Residuen dar, d. h. jeder Restplot, den Sie mit einem beliebigen Modell betrachten, befindet sich auf derselben standardisierten y-Achse.)
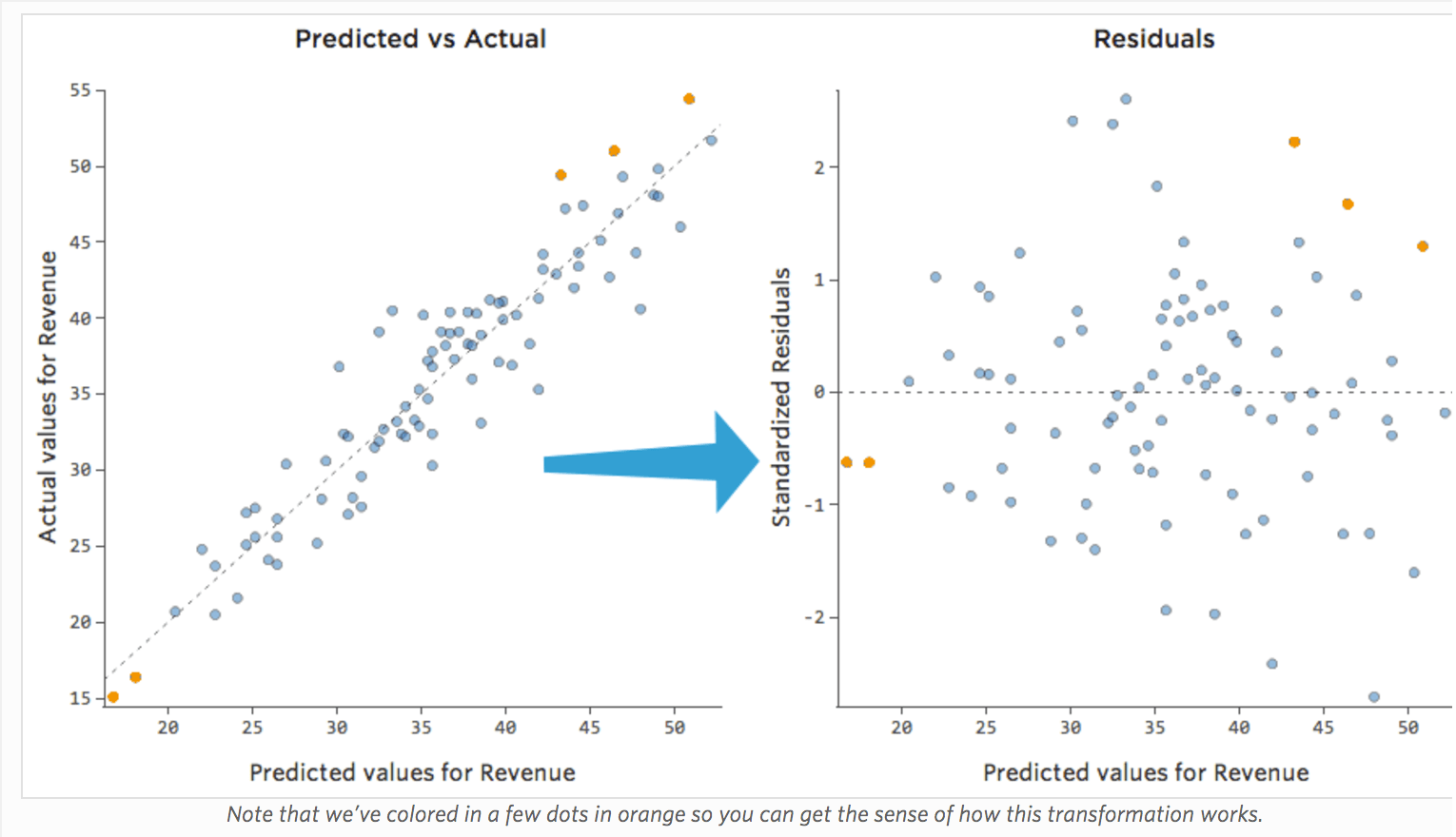
Im Diagramm auf der rechten Seite entspricht jeder Punkt einem Tag, wobei sich die Prognose des Modells auf der X-Achse und die Genauigkeit der Prognose auf der Y-Achse befindet. Der Abstand von der Linie bei 0 gibt an, wie schlecht die Prognose für diesen Wert war.
Seit …
Restwert = beobachtet – prognostiziert
… positive Werte für den Rest (auf der y-Achse) bedeuten, dass die Prognose zu niedrig war und negative Werte bedeuten, dass die Prognose zu hoch war; 0 bedeutet, dass die Vermutung genau korrekt war.
Im Idealfall sieht das Restwertdiagramm so aus:
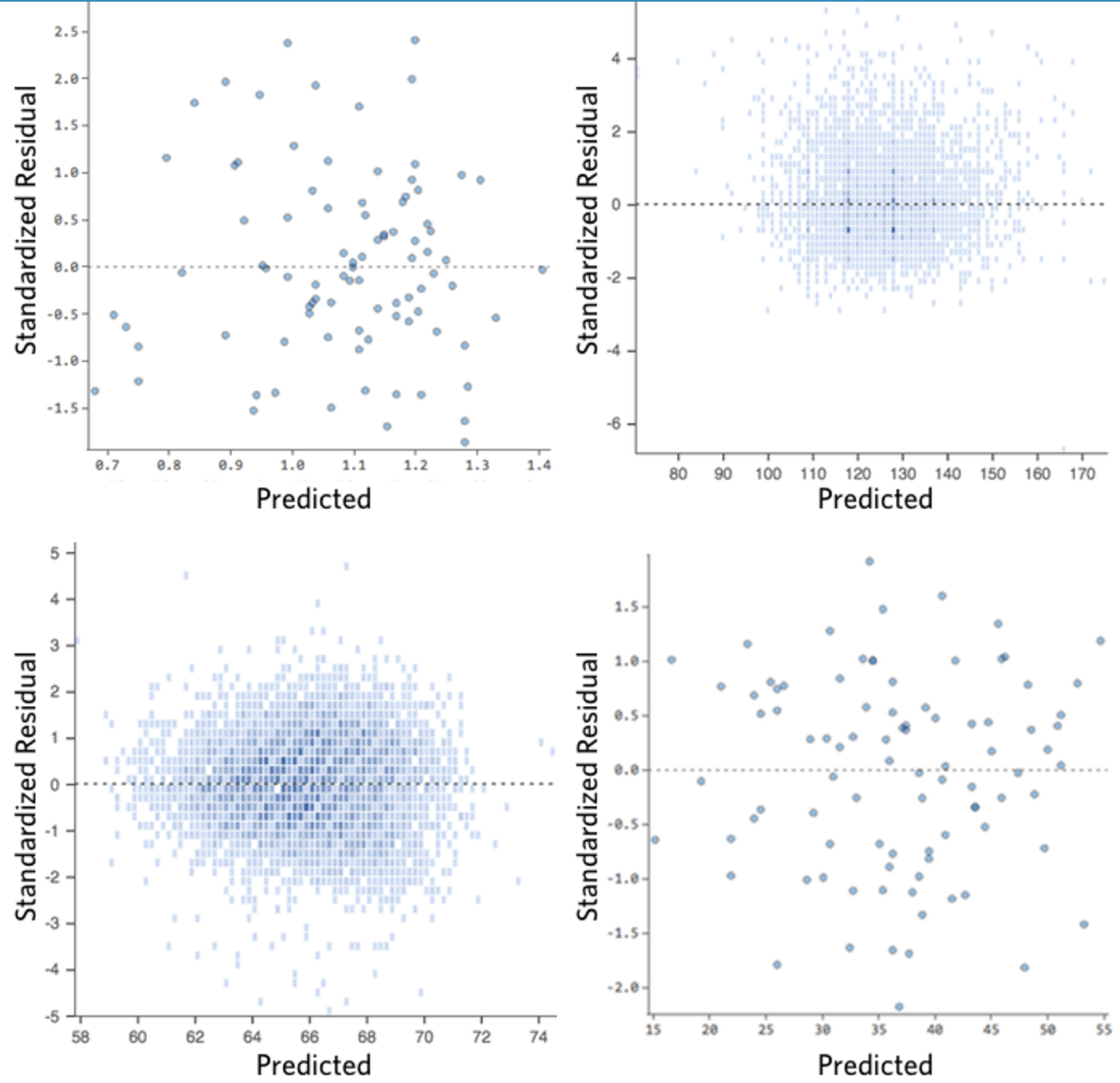
Das heißt,
(1) sie sind ziemlich symmetrisch verteilt und tendieren dazu, sich in der Mitte des Diagramms hin zu konzentrieren.
(2) sie sind um die unteren Einzelziffern der y-Achse geclustert (z. B. 0,5 oder 1,5, nicht 30 oder 150).
(3) im Allgemeinen gibt es keine klaren Muster.
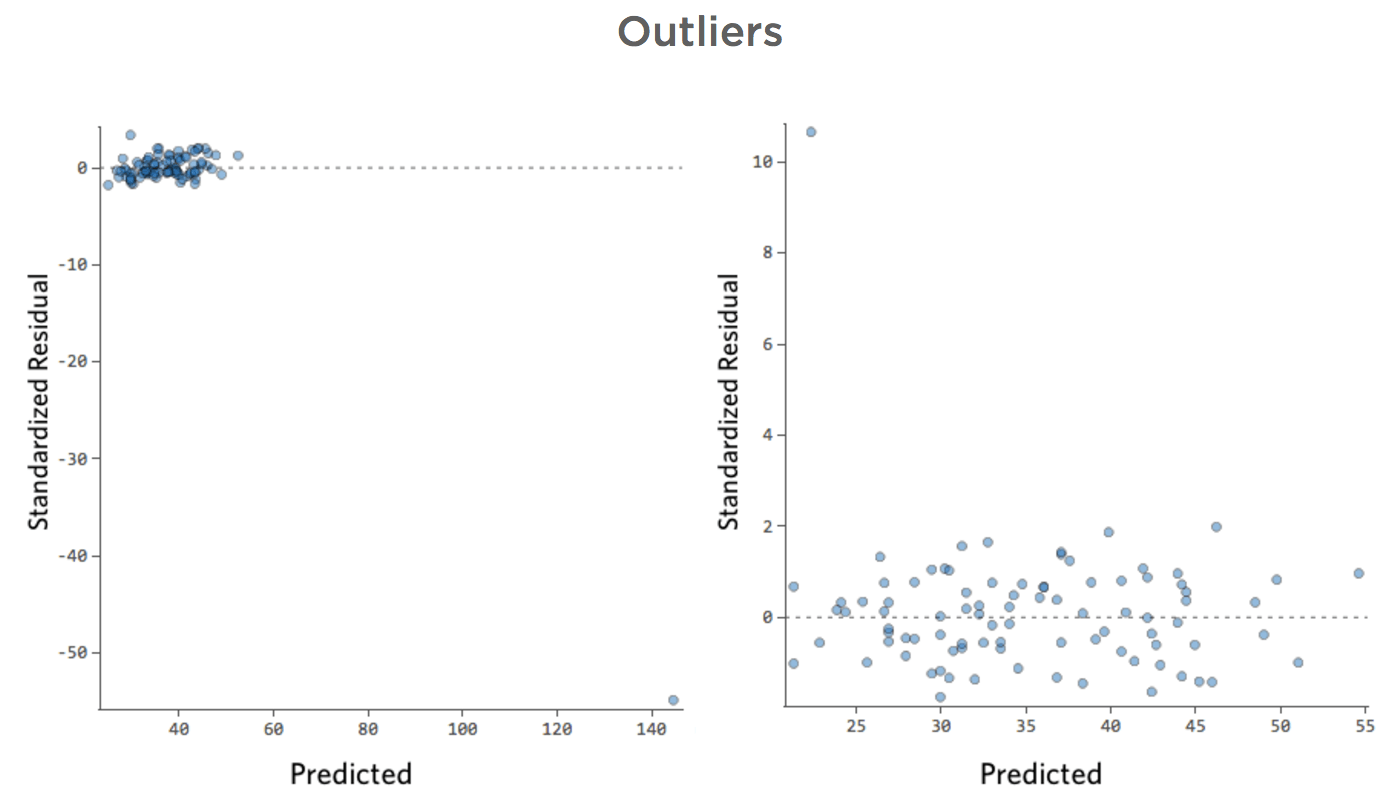
Im Folgenden finden Sie einige Restwertdiagramme, die diese Anforderungen nicht erfüllen:
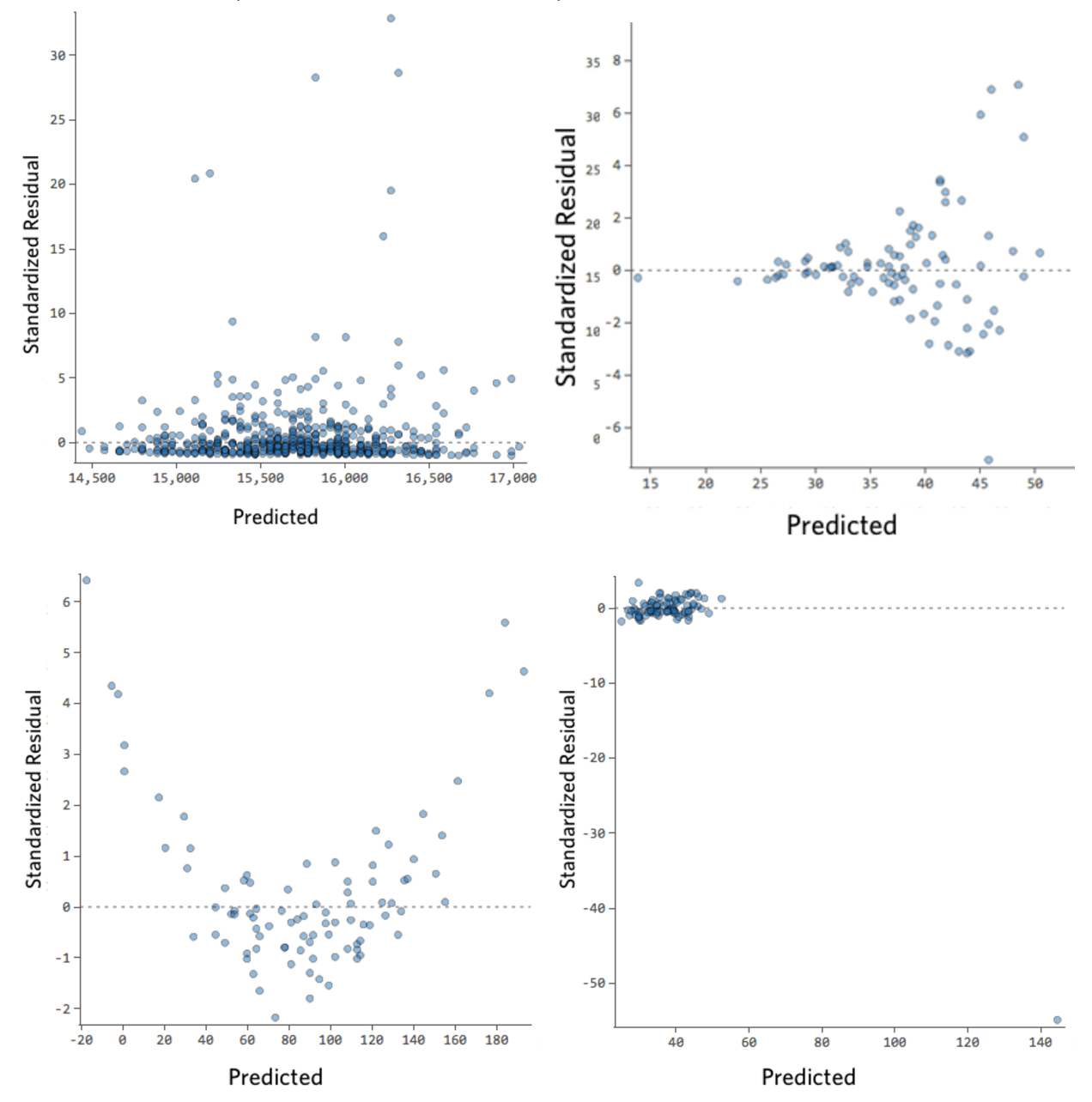
Diese Bereiche sind nicht gleichmäßig vertikal verteilt, haben einen Ausreißer oder haben eine klare Form für sie.
Wenn Sie ein klares Muster oder einen klaren Trend in Ihren Residuen erkennen, kann Ihr Modell verbessert werden.
In einer Sekunde werden wir aufschlüsseln, warum und was wir dagegen tun müssen.
Normales Q-Q-Restdiagramm:
Klicken Sie auf Normales Q-Q-Restdiagramm anzeigen, um ein Q-Q-Diagramm anzuzeigen, das Datenschiefe und Modellanpassung bewertet. Dieses Diagramm zeigt die standardisierten Residuen auf der Y-Achse und die theoretischen Quantile auf der X-Achse an.
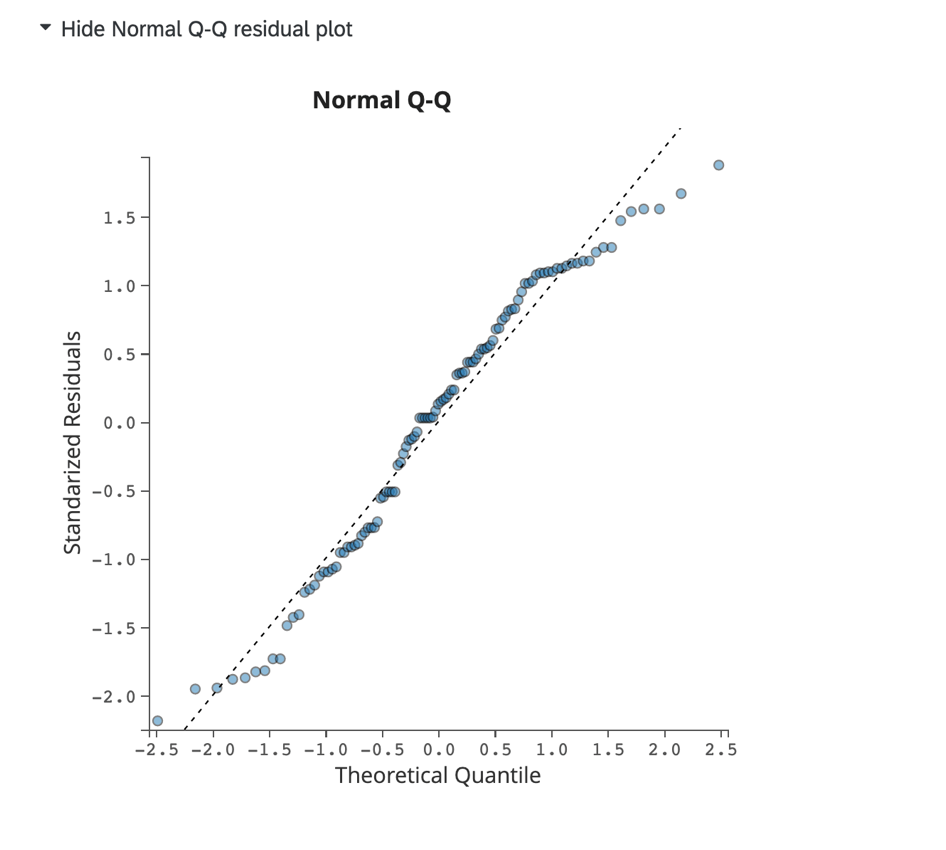 Daten, die eng an der gepunkteten Linie ausgerichtet sind, weisen auf eine Normalverteilung hin. Wenn die Punkte drastisch von der Linie abweichen, könnten Sie in Erwägung ziehen, Ihr Modell anzupassen, indem Sie andere Variablen im Regressionsmodell hinzufügen oder entfernen.
Daten, die eng an der gepunkteten Linie ausgerichtet sind, weisen auf eine Normalverteilung hin. Wenn die Punkte drastisch von der Linie abweichen, könnten Sie in Erwägung ziehen, Ihr Modell anzupassen, indem Sie andere Variablen im Regressionsmodell hinzufügen oder entfernen.
Wie wichtig ist es, wenn mein Modell nicht perfekt ist?
Wie besorgt sollten Sie sein, wenn Ihr Modell nicht perfekt ist, wenn Ihre Residuen ein bisschen ungesund aussehen? Das liegt an Ihnen.
Wenn Sie Ihre Arbeit in der Teilchenphysik veröffentlichen, möchten Sie wahrscheinlich sicherstellen, dass Ihr Modell so genau wie menschlich möglich ist. Wenn Sie versuchen, eine schnelle und schmutzige Analyse des Limonadenstands Ihres Neffen durchzuführen, könnte ein weniger perfektes Modell gut genug sein, um alle Fragen zu beantworten, die Sie haben (z. B. ob „Temperatur“ sich auf den Umsatz auswirkt).
Meistens ist ein anständiges Modell besser als gar keines. Nehmen Sie also Ihr Modell, versuchen Sie es zu verbessern, und entscheiden Sie dann, ob die Genauigkeit gut genug ist, um für Ihre Zwecke nützlich zu sein.
Beispiel Restplots und deren Diagnosen
Wenn Sie sich nicht sicher sind, was ein Rest ist, nehmen Sie sich fünf Minuten Zeit, um das oben Gesagte zu lesen, und kehren Sie dann hierher zurück.
Darunter befindet sich eine Galerie ungesunder Restplots. Ihr Rest kann wie ein bestimmter Typ von unten oder eine Kombination aussehen.
Wenn Sie so aussehen, wie eines der folgenden Elemente aussieht, klicken Sie darauf, um zu verstehen, was vor sich geht, und erfahren Sie, wie Sie das Problem beheben können.
(Wir verwenden den „Umsatz“ eines Limonadenstandes im Vergleich zur „Temperatur“ dieses Tages als Beispieldatenset.)
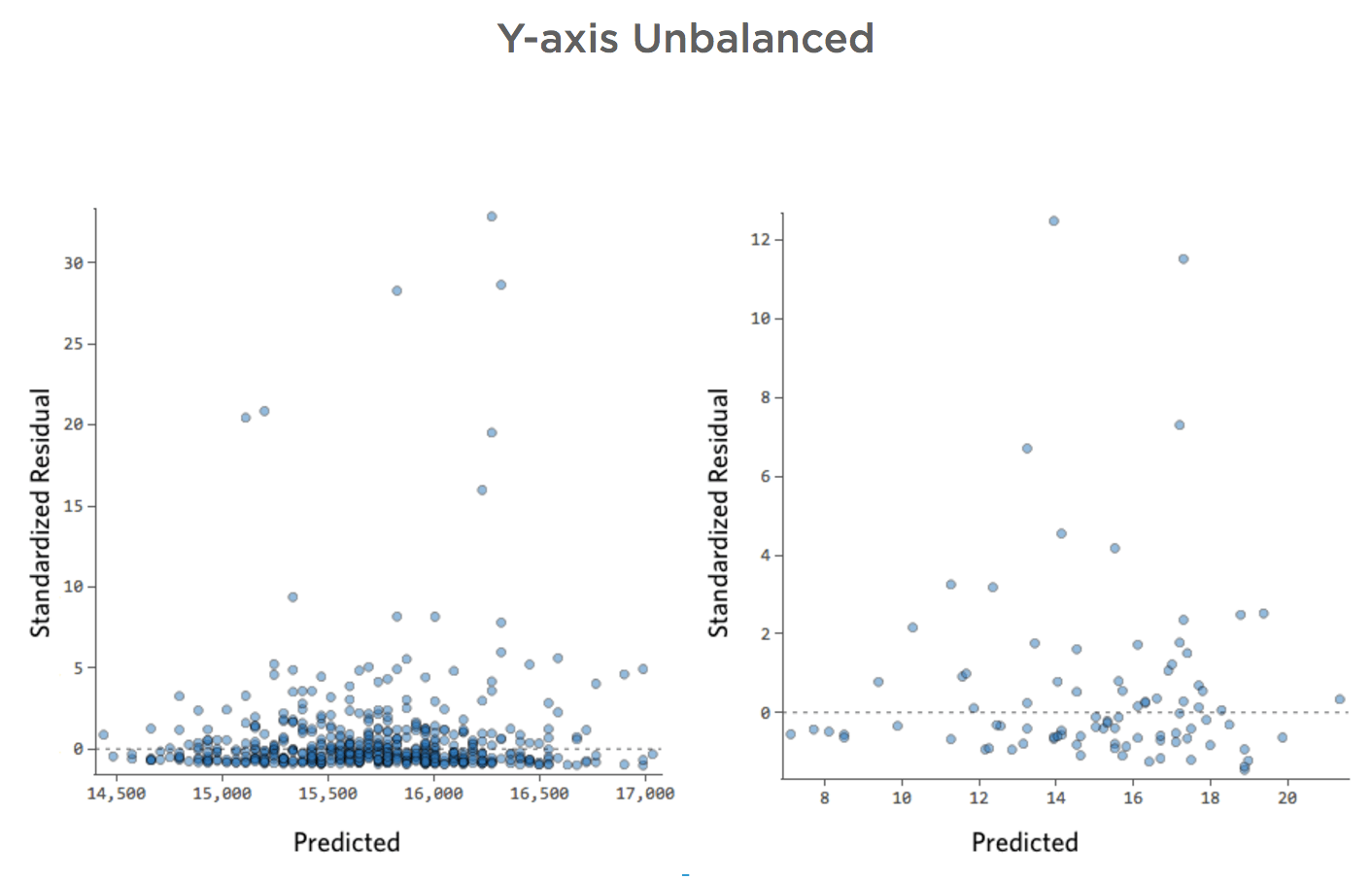
Y-Achse nicht ausgeglichen
- Details zu diesem Diagramm und wie Sie es reparieren können.
-
Problem
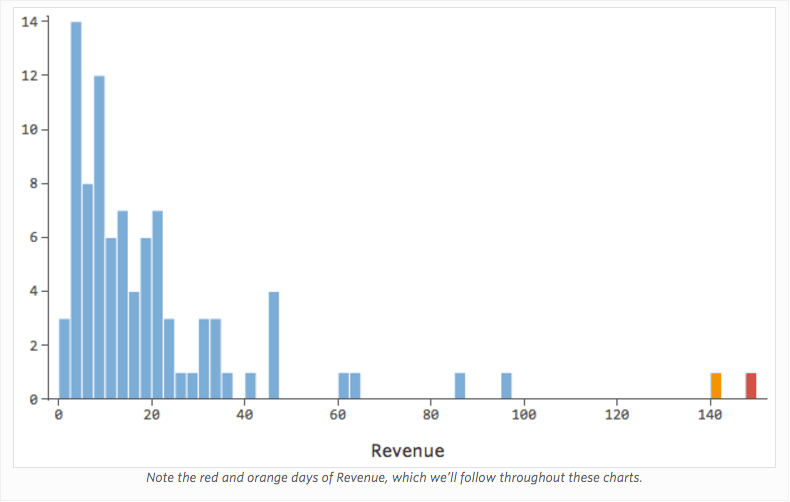
Stellen Sie sich vor, aus welchen Gründen auch immer, Ihr Limonade-Stand hat in der Regel einen niedrigen Umsatz, aber immer wieder bekommst du sehr hohe Umsatztage, so dass „Umsatz“ so aussah …
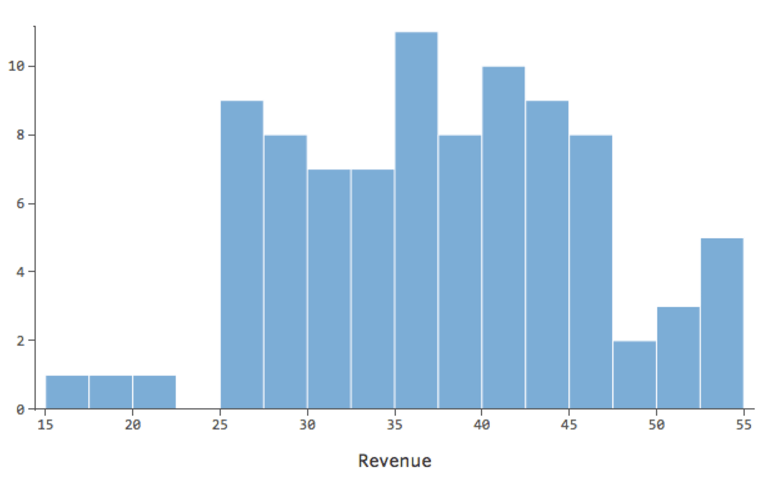
… statt etwas symmetrischeres und glockenförmiges wie das folgende:
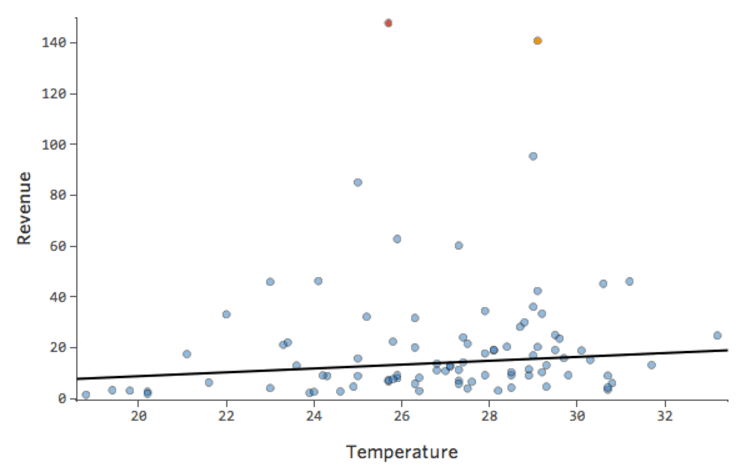
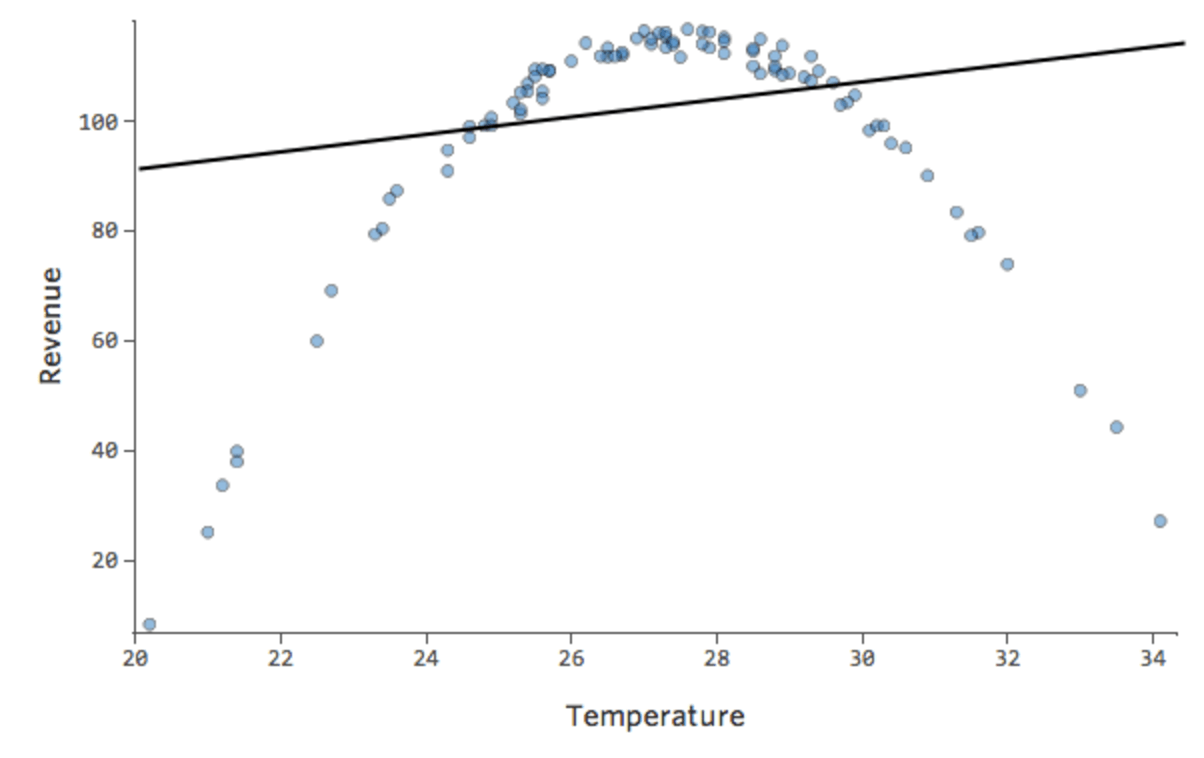
Also „Temperatur“ vs. „Umsatz“ könnte wie folgt aussehen, wobei die meisten Daten unten gebündelt sind …
Die schwarze Linie stellt die Modellgleichung dar, die Vorhersage der Beziehung zwischen „Temperatur“ und „Umsatz“. Sehen Sie sich oben jede Prognose an, die von der schwarzen Linie für eine bestimmte „Temperatur“ erstellt wurde (z. B. wird bei „Temperatur“ 30 der Umsatz auf etwa 20 prognostiziert). Sie sehen, dass der Großteil der Punkte unterhalb der Linie liegt (d. h. die Vorhersage war zu hoch), aber einige Punkte befinden sich sehr weit über der Linie (d. h. die Vorhersage war viel zu niedrig).
Wenn Sie dieselben Daten in die Diagnosediagramme übersetzen, sind die meisten Prognosen der Gleichung etwas zu hoch und einige wären dann viel zu niedrig.
Auswirkungen
Dies bedeutet fast immer, dass Ihr Modell deutlich genauer werden kann. Meistens stellen Sie fest, dass das Modell im Vergleich zu einer verbesserten Version direkt korrekt, aber ziemlich ungenau war. Es ist nicht ungewöhnlich, ein solches Problem zu beheben und somit den r-quadrierten Sprung des Modells von 0,2 auf 0,5 (auf einer Skala von 0 bis 1) zu sehen.
So beheben Sie das Problem
- Die Lösung hierfür besteht fast immer darin, Ihre Daten zu transformieren, in der Regel Ihre Response-Variable.
- Es ist auch möglich, dass in Ihrem Modell eine Variable fehlt.
Heteroskedastizität
- Details zu diesem Diagramm und wie Sie es reparieren können.
-
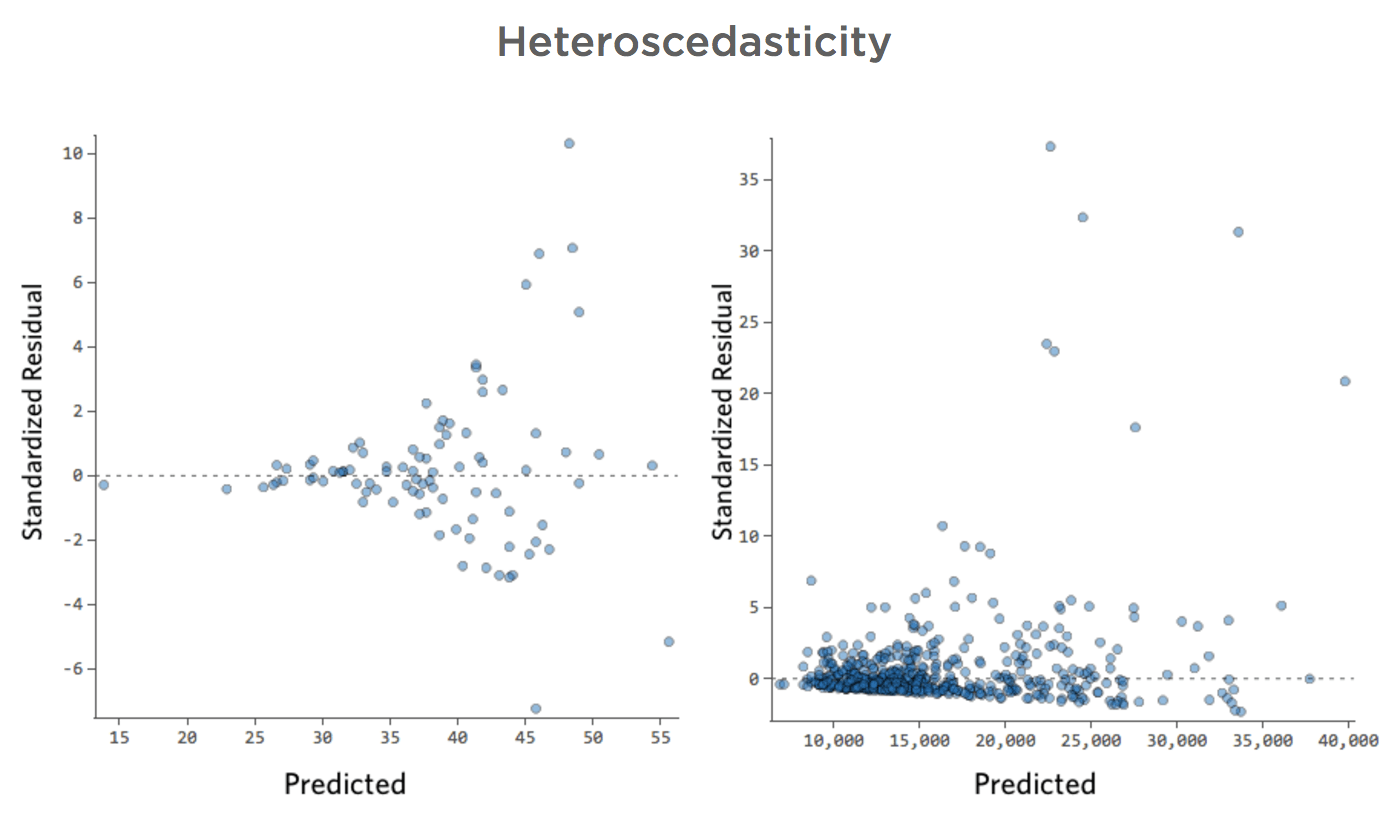
Problem
Diese Parzellen weisen eine „Heteroskedastizität“ auf, was bedeutet, dass die Residuen größer werden, wenn die Prognose von klein zu groß (oder von groß zu klein) wechselt.
Stellen Sie sich vor, an kalten Tagen ist der Umsatz sehr konsistent, aber an heißeren Tagen ist der Umsatz manchmal sehr hoch und manchmal sehr niedrig.
Folgende Diagramme werden angezeigt:
Auswirkungen
Dies führt nicht von Natur aus zu einem Problem, aber es ist oft ein Indikator dafür, dass Ihr Modell verbessert werden kann.
Die einzige Ausnahme besteht darin, dass Ihre p-Werte etwas höher oder niedriger sein können, wenn Ihre Stichprobengröße unter 250 liegt und Sie das Problem nicht mithilfe der folgenden Angaben beheben können. Ihre p-Werte können etwas höher oder niedriger als sie sein sollten, sodass möglicherweise eine Variable, die sich direkt am Signifikanzrand befindet, fälschlicherweise auf der falschen Seite dieses Rahmens landet. Ihre Regressionskoeffizienten (die Anzahl der Einheiten „Umsatz“ ändert sich, wenn „Temperatur“ um eins steigt) sind jedoch immer noch genau.
So beheben Sie das Problem
- Die am häufigsten erfolgreiche Lösung besteht darin, eine Variable zu transformieren.
- Häufig deutet die Heteroskedastizität darauf hin, dass eine Variable fehlt.
Nichtlinear
- Details zu diesem Diagramm und wie Sie es reparieren können.
-
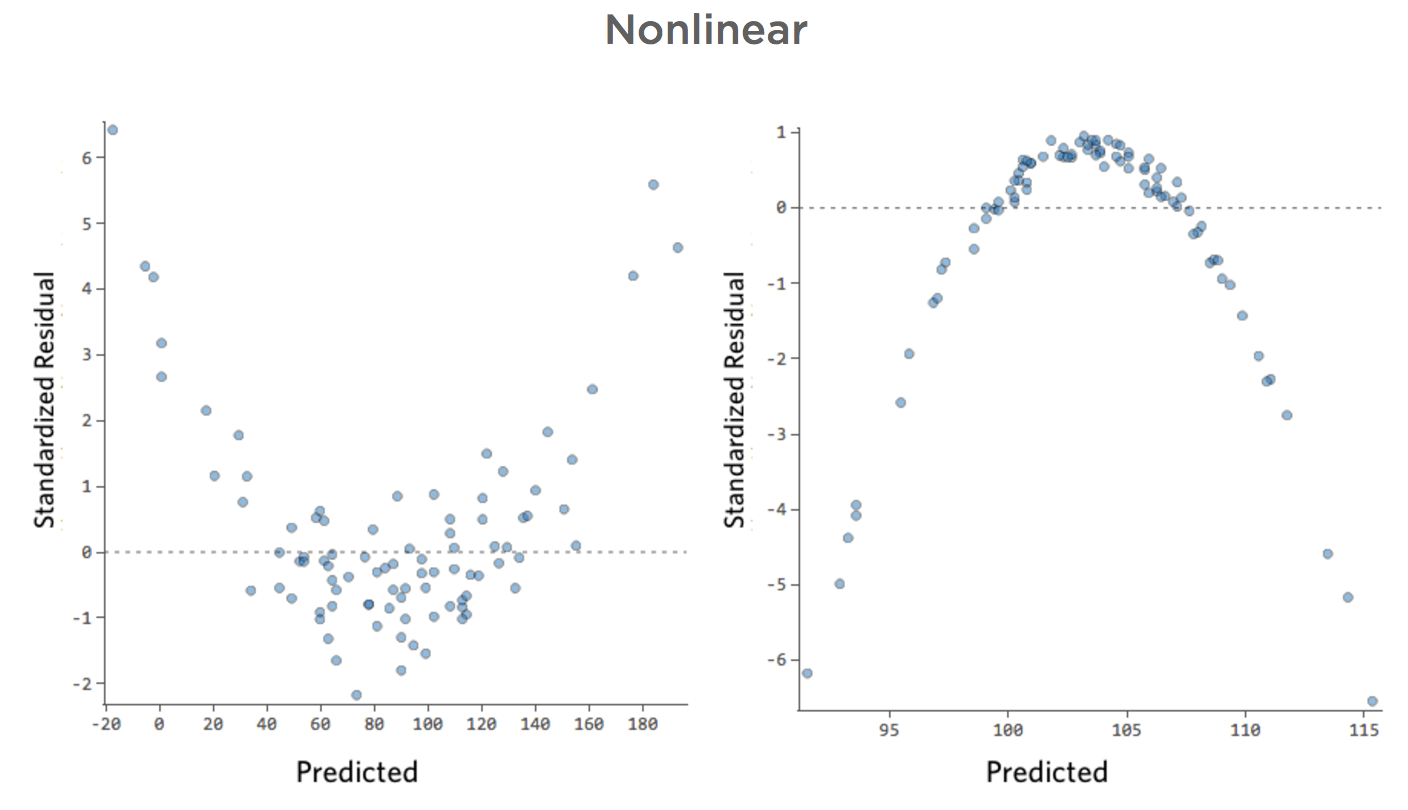
Problem
Stellen Sie sich vor, es ist schwierig, Limonade an kalten Tagen zu verkaufen, sie an warmen Tagen einfach zu verkaufen und an sehr heißen Tagen nur schwer zu verkaufen (vielleicht, weil niemand ihr Haus an sehr heißen Tagen verlässt).
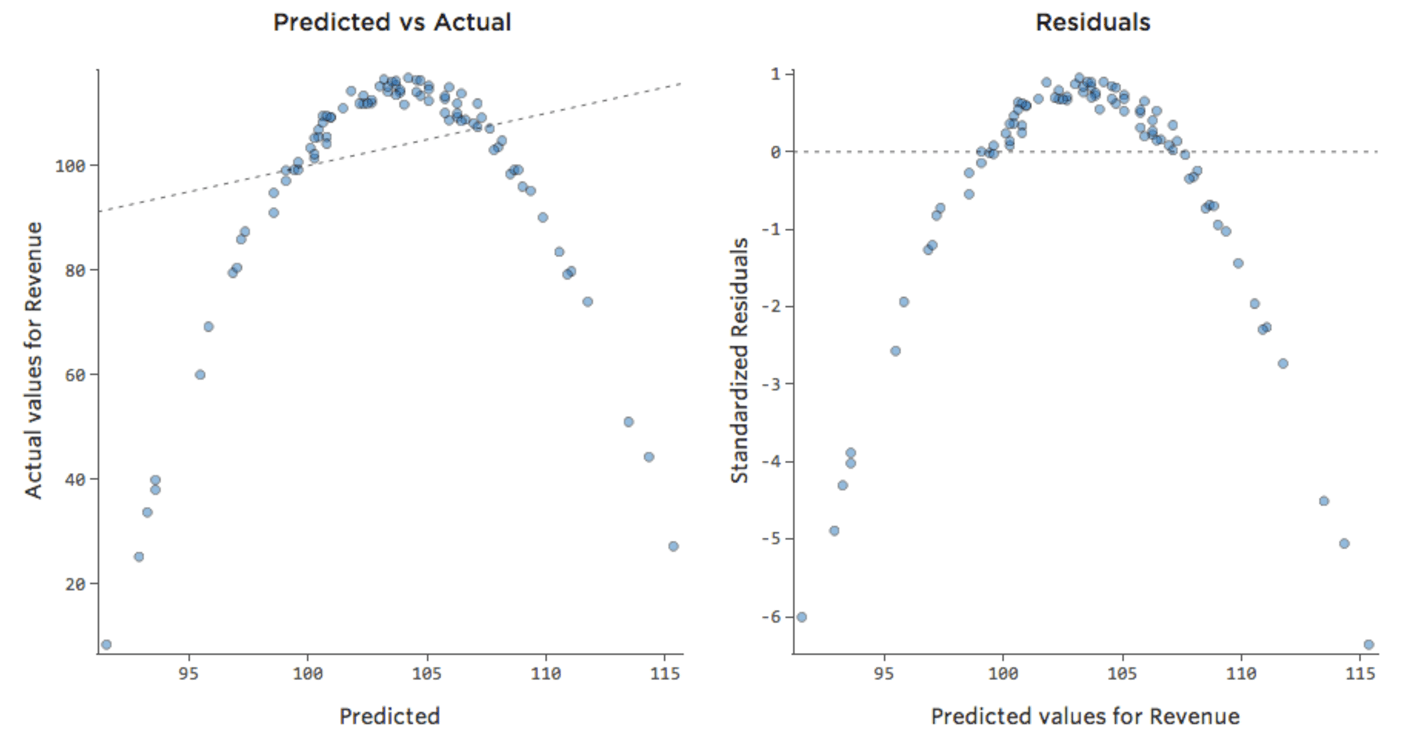
Dieser Plot würde wie folgt aussehen:
Das Modell, dargestellt durch die Linie, ist schrecklich. Die Vorhersagen wären weit entfernt, d. h., Ihr Modell stellt die Beziehung zwischen „Temperatur“ und „Umsatz“ nicht genau dar.
Dementsprechend würden Residuen wie folgt aussehen:
Auswirkungen
Wenn Ihr Modell entfernt ist, wie im obigen Beispiel, sind Ihre Prognosen ziemlich wertlos (und Sie stellen fest, dass das R-Quadrat sehr niedrig ist, wie das Quadrat von 0,027 für die oben genannten).
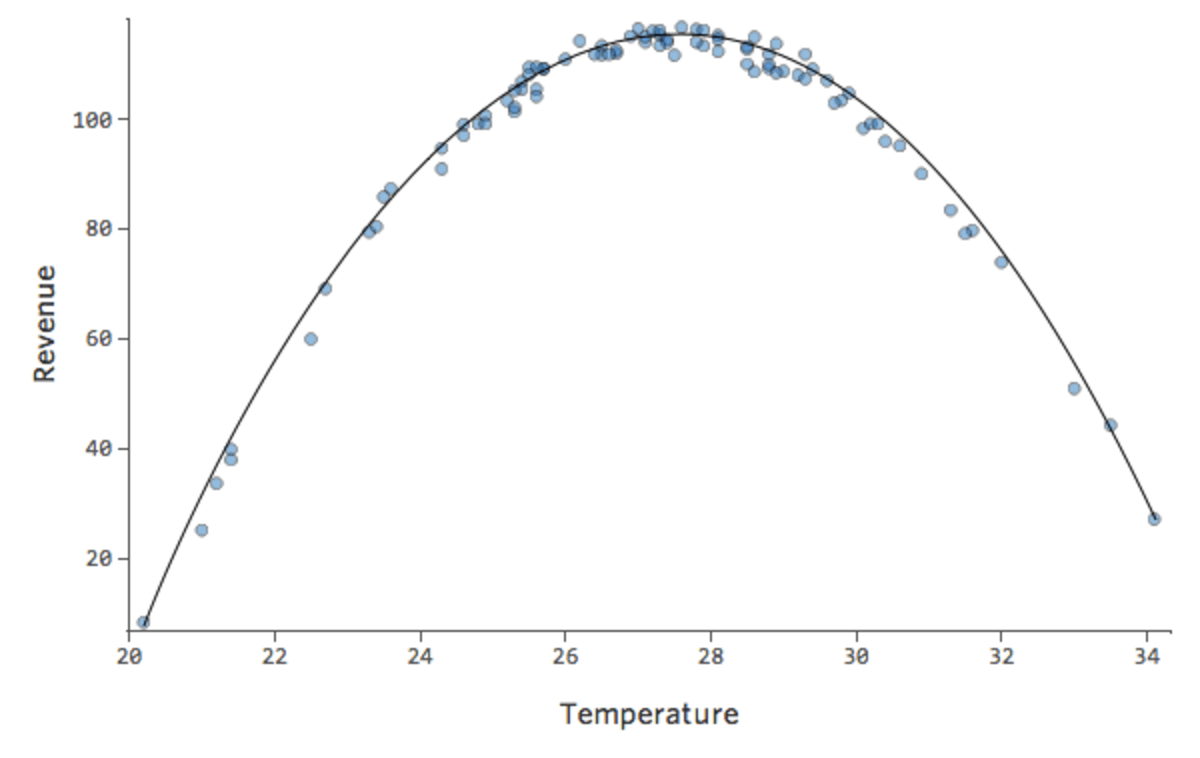
In anderen Fällen vermittelt Ihnen eine leicht suboptimale Anpassung dennoch einen guten allgemeinen Sinn für die Beziehung, auch wenn sie nicht perfekt ist, wie im Folgenden dargestellt:
Dieses Modell sieht ziemlich genau aus. Wenn man genau hinschaut (oder wenn man sich die Residuen anschaut), kann man erkennen, dass es hier ein bisschen ein Muster gibt – dass die Punkte auf einer Kurve stehen, dass die Linie nicht ganz übereinstimmt.
Macht das was aus? Das liegt an Ihnen. Wenn Sie die Beziehung schnell verstehen, ist Ihre Gerade eine ziemlich anständige Annäherung. Wenn Sie dieses Modell für die Vorhersage und nicht für Erklärungen verwenden, würde wahrscheinlich das genaueste Modell diese Kurve berücksichtigen.
So beheben Sie das Problem
- Manchmal weisen Muster wie diese darauf hin, dass eine Variable transformiert werden muss.
- Wenn das Muster tatsächlich so klar ist wie in diesen Beispielen, müssen Sie wahrscheinlich ein nichtlineares Modell erstellen (es ist nicht so schwer, wie das klingt).
- Oder wie immer ist es möglich, dass es sich um eine fehlende Variable handelt.
Ausreißer
- Details zu diesem Diagramm und wie Sie es reparieren können.
-
Problem
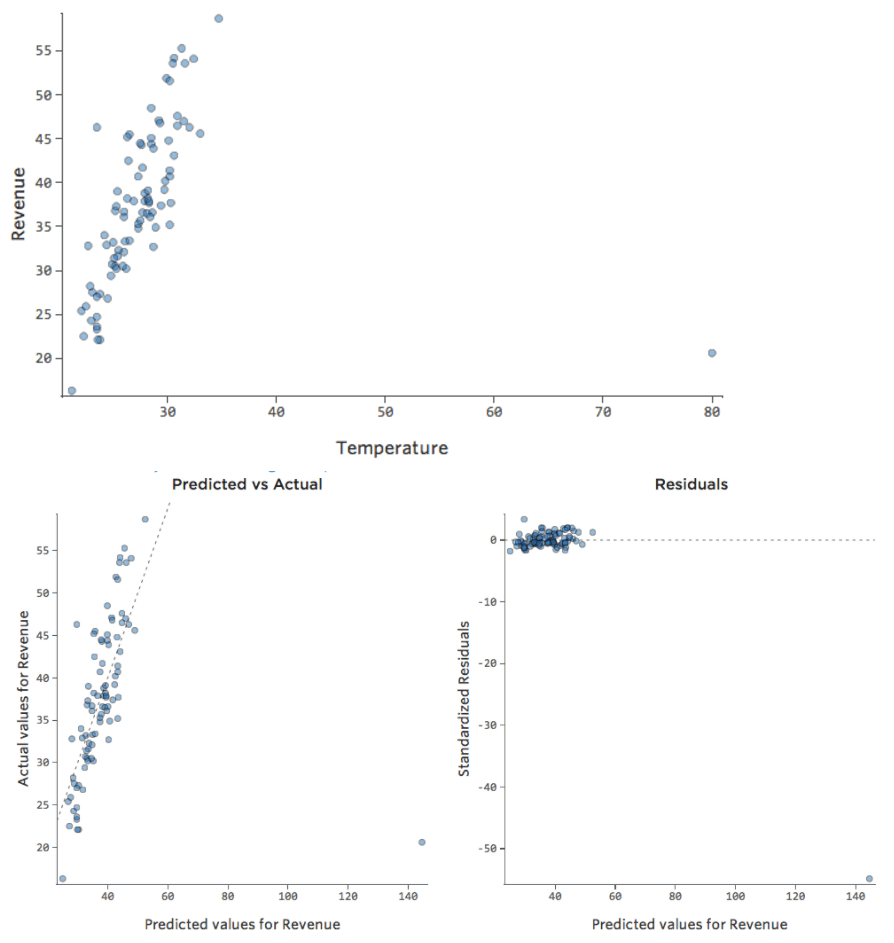
Was ist, wenn einer Ihrer Datenpunkte statt der normalen 20er und 30er eine „Temperatur“ von 80 hat? Ihre Plots würden wie folgt aussehen:
Diese Regression hat einen ausstehenden Datenpunkt für die Eingabevariable „Temperatur“ (Ausreißer für eine Eingabevariable werden auch als „Hebelpunkte“ bezeichnet).
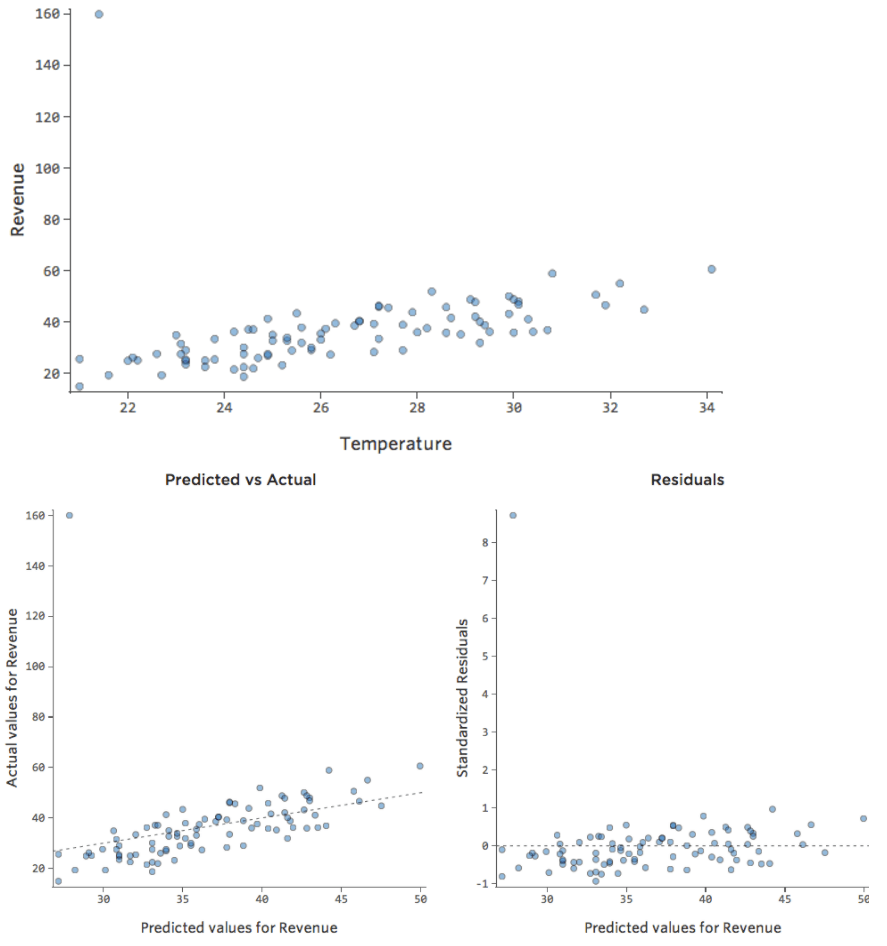
Was wäre, wenn einer Ihrer Datenpunkte statt der normalen 20–60 USD 160 USD an Umsatz hätte? Ihre Plots würden wie folgt aussehen:
Diese Regression hat einen ausstehenden Datenpunkt für die Ausgabevariable „Umsatz“.
Auswirkungen
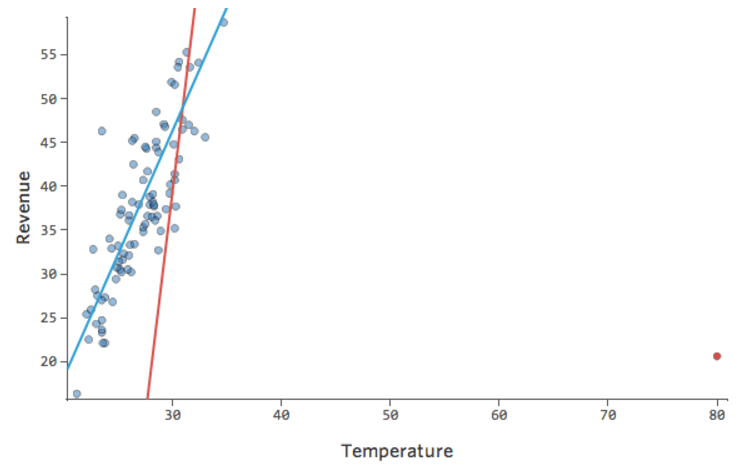
Stats iQ führt eine Regressionsart aus, die im Allgemeinen nicht von Ausgabeausreißern betroffen ist (wie der Tag mit einem Umsatz von 160 USD), aber von Eingabeausreißern (wie eine „Temperatur“ in den 80ern). Im schlimmsten Fall kann Ihr Modell versuchen, sich diesem Punkt anzunähern, und zwar zu Lasten der Nähe zu allen anderen, und am Ende einfach völlig falsch sein, z. B.:
Die blaue Linie entspricht wahrscheinlich dem Aussehen Ihres Modells, und die rote Linie ist das Modell, das Sie möglicherweise sehen, wenn Sie diesen Ausreißer bei „Temperatur“ 80 haben.
So beheben Sie das Problem
- Es ist möglich, dass es sich um einen Mess- oder Dateneingabefehler handelt, bei dem der Ausreißer nur falsch ist. In diesem Fall sollten Sie ihn löschen.
- Es ist möglich, dass das, was nur ein paar Ausreißer zu sein scheint, tatsächlich eine Stromverteilung ist. Ziehen Sie in Betracht, die Variable zu transformieren, wenn eine Ihrer Variablen eine asymmetrische Verteilung hat (d. h., sie ist nicht ansatzweise glockenförmig).
- Wenn es sich tatsächlich um einen legitimen Ausreißer handelt, sollten Sie die Auswirkungen des Ausreißers bewerten.
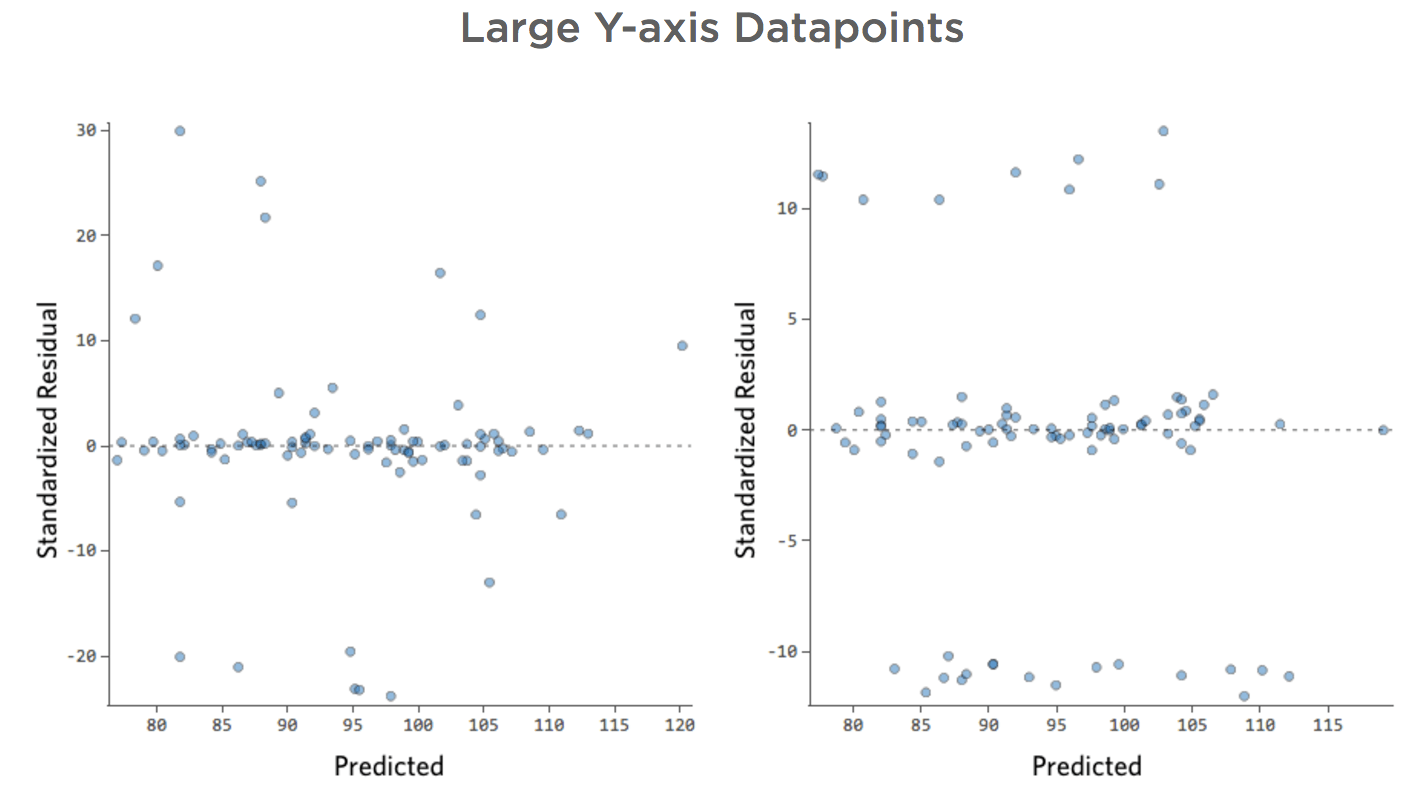
Große Y-Achsen-Datenpunkte
- Details zu diesem Diagramm und wie Sie es reparieren können.
-
Problem
Stellen Sie sich vor, es gibt zwei konkurrierende Limonadenstände in der Nähe. Meistens ist nur eine davon betriebsbereit. In diesem Fall ist Ihr Umsatz durchgängig gut. Manchmal ist keines von beiden aktiv, und der Umsatz nimmt ab; zu anderen Zeiten sind beide aktiv und es gibt Umsatzeinbußen.
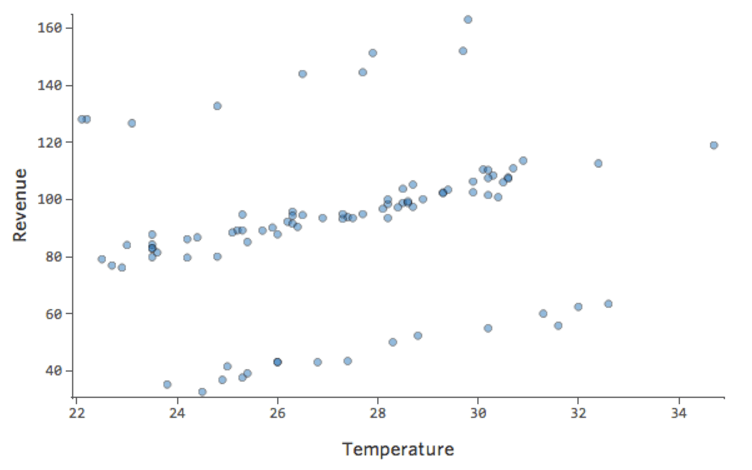
„Umsatz“ vs. „Temperatur“ könnte so aussehen …
… wobei diese oberste Zeile Tage sind, wenn kein anderer Stand angezeigt wird, und die unterste Zeile Tage, wenn beide anderen Tribünen im Geschäft sind.
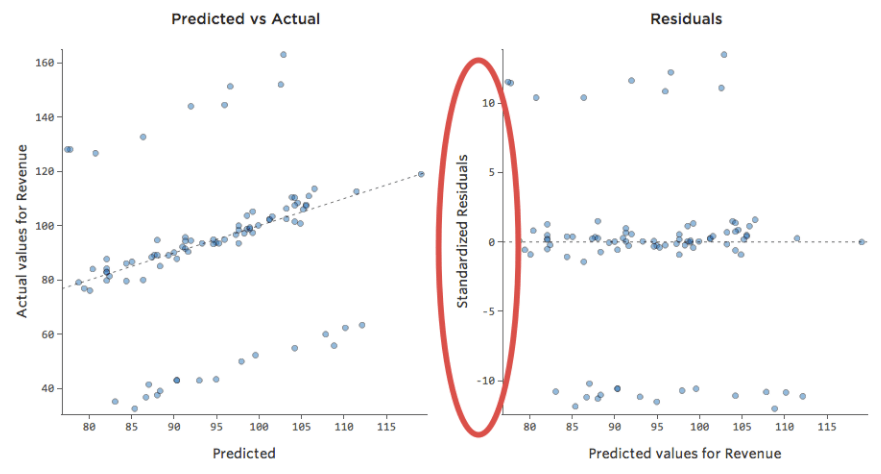
Daraus würden sich folgende Restplots ergeben:
Das heißt, es gibt einige Datenpunkte auf beiden Seiten von 0, die Residuen von 10 oder höher aufweisen, was bedeutet, dass das Modell weit entfernt war.
Wenn Sie nun täglich Daten für eine Variable mit der Bezeichnung „Anzahl aktiver Limonadenständer“ erfassen würden, können Sie diese Variable Ihrem Modell hinzufügen, und dieses Problem wäre behoben. Oft haben Sie jedoch nicht die Daten, die Sie benötigen (oder sogar eine Vermutung darüber, welche Art von Variable Sie benötigen).
Auswirkungen
Ihr Modell ist nicht wertlos, aber es ist definitiv nicht so gut, als wenn Sie alle benötigten Variablen hätten. Du könntest es immer noch verwenden und so etwas wie sagen: „Dieses Modell ist meistens ziemlich genau, aber dann jedes Mal und ab.“ Ist das nützlich? Wahrscheinlich, aber das ist Ihre Entscheidung und es hängt davon ab, welche Entscheidungen Sie basierend auf Ihrem Modell treffen möchten.
So beheben Sie das Problem
- Auch wenn dieser Ansatz in dem oben genannten Beispiel nicht funktionieren würde, lohnt es sich fast immer, sich umzusehen, ob es die Möglichkeit gibt, eine Variable sinnvoll zu transformieren.
- Wenn das jedoch nicht funktioniert, müssen Sie wahrscheinlich Ihr Problem mit fehlenden Variablen lösen.
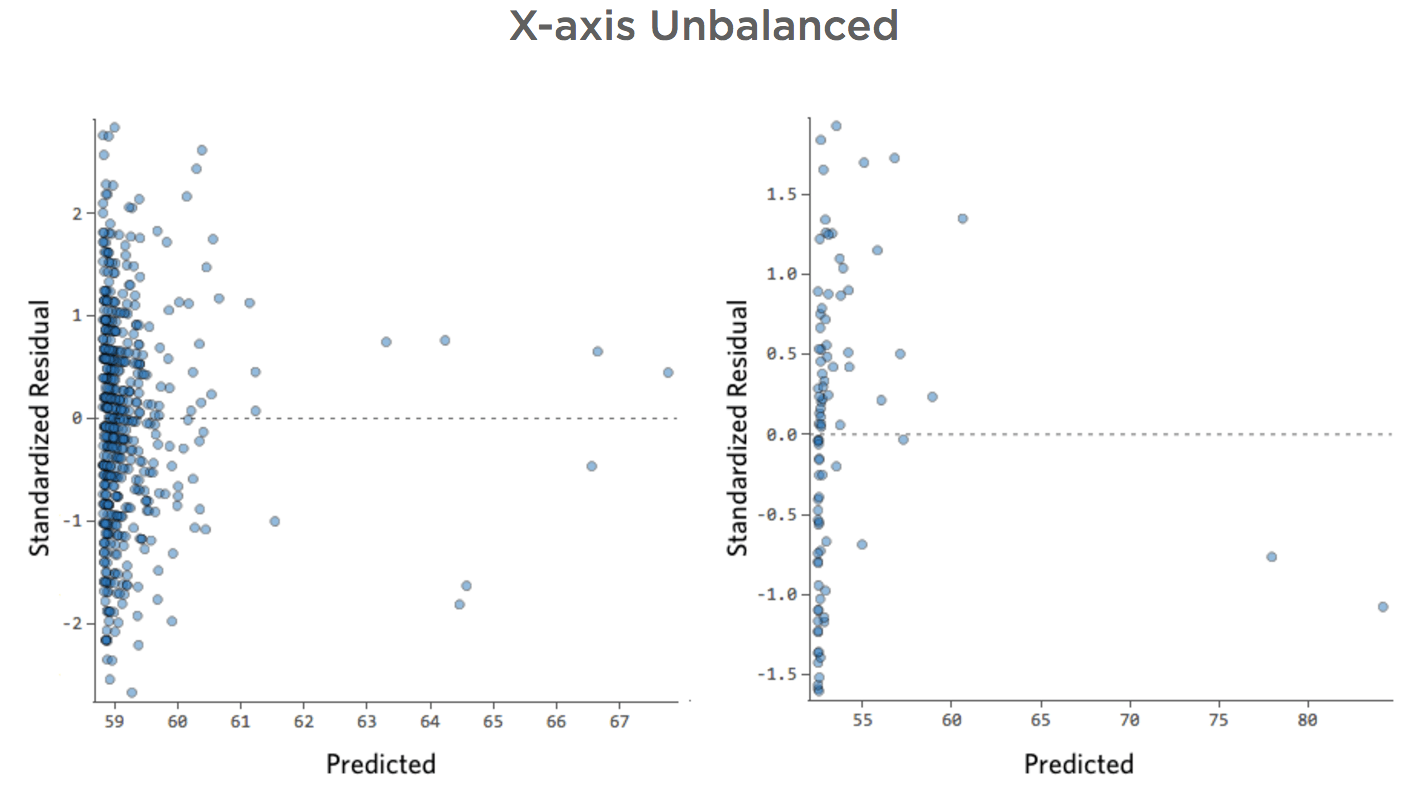
X-Achse nicht ausgeglichen
- Details zu diesem Diagramm und wie Sie es reparieren können.
-
Problem
Stellen Sie sich vor, „Umsatz“ wird durch den nahegelegenen „Fußverkehr“ zusätzlich oder anstelle von „Temperatur“ angetrieben. Stellen Sie sich vor, aus welchen Gründen auch immer, Ihr Limonadenstand hat in der Regel einen niedrigen Umsatz, aber immer wieder bekommen Sie extrem hohe Umsatztage, so dass Ihr Umsatz so aussah…
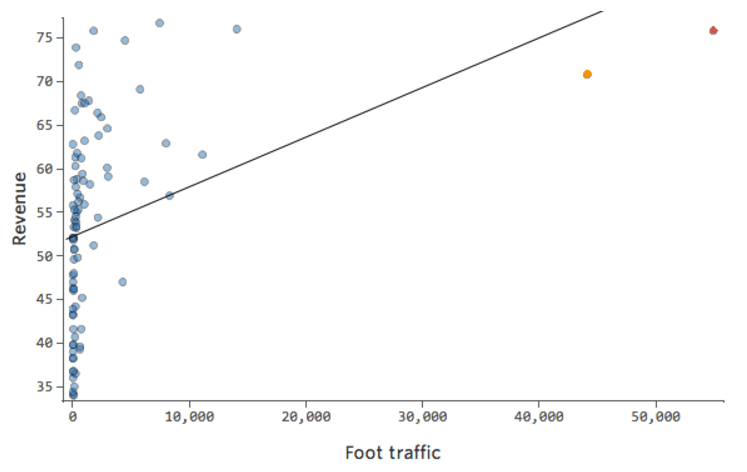
Also könnte „Fußverkehr“ vs. „Umsatz“ wie folgt aussehen, wobei die meisten Daten auf der linken Seite angezeigt werden:
Die schwarze Linie stellt die Modellgleichung dar, die Vorhersage der Beziehung zwischen „Fußverkehr“ und „Umsatz“. Sie sehen, dass das Modell nicht wirklich den Unterschied zwischen „Fußverkehr“ von 0 und von beispielsweise 100 oder 1.000 unterscheiden kann. Für jeden dieser Werte würde der Umsatz bei 53 US-Dollar prognostiziert.
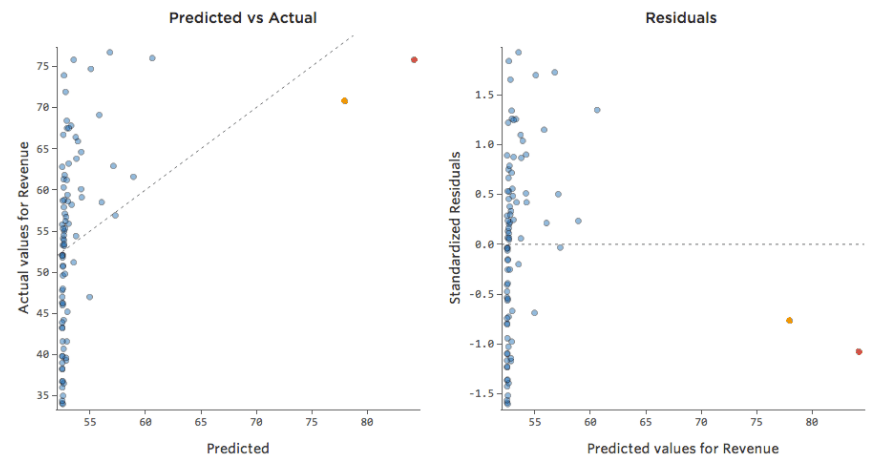
Übersetzen derselben Daten in die Diagnosediagramme:
Auswirkungen
Manchmal stimmt eigentlich nichts mit Ihrem Modell. Im obigen Beispiel ist es ganz klar, dass dies kein gutes Modell ist, aber manchmal ist der Restplot unausgewogen und das Modell ziemlich gut.
Die einzige Möglichkeit, dies zu erkennen, besteht darin, a) mit der Transformation Ihrer Daten zu experimentieren und zu prüfen, ob Sie sie verbessern können, und b) den prognostizierten vs. tatsächlichen Graphen zu betrachten und zu prüfen, ob Ihre Prognose für viele Datenpunkte absichtlich ist, wie im obigen Beispiel (im Gegensatz zum Beispiel unten).
Es gibt zwar keine explizite Regel, die besagt, dass Ihr Rest nicht unausgewogen und dennoch genau sein kann (dieses Modell ist sogar ziemlich genau), aber es ist öfter der Fall, dass eine unausgeglichene x-Achse dazu führt, dass Ihr Modell deutlich genauer gestaltet werden kann. Meistens stellen Sie fest, dass das Modell im Vergleich zu einer verbesserten Version direkt korrekt, aber ziemlich ungenau war. Es ist nicht ungewöhnlich, ein solches Problem zu beheben und somit den r-quadrierten Sprung des Modells von 0,2 auf 0,5 (auf einer Skala von 0 bis 1) zu sehen.
So beheben Sie das Problem
- Die Lösung hierfür ist fast immer die Transformation Ihrer Daten, in der Regel eine erklärende Variable. (Beachten Sie, dass das unten gezeigte Beispiel auf die Transformation Ihrer Response-Variable verweist, aber derselbe Prozess hier hilfreich ist.)
- Es ist auch möglich, dass in Ihrem Modell eine Variable fehlt.
Verbessern Ihres Modells: Bewertung der Auswirkungen eines Ausreißers
Angenommen, Sie haben einen Datenpunkt außerhalb des Bereichs, der legitim ist, kein Mess- oder Datenfehler. Um zu entscheiden, wie Sie fortfahren möchten, sollten Sie die Auswirkungen des Datenpunkts auf die Regression bewerten.
Sie können dies am einfachsten tun, indem Sie die Koeffizienten Ihres aktuellen Modells notieren und dann diesen Datenpunkt aus der Regression herausfiltern. Wenn sich das Modell nicht viel ändert, dann muss man sich nicht viel Sorgen machen.
Wenn sich das Modell dadurch signifikant ändert, untersuchen Sie das Modell (insbesondere Ist vs. Prognose), und entscheiden Sie, welches Modell sich für Sie besser fühlt. Es ist in Ordnung, den Ausreißer letztendlich zu verwerfen, solange man theoretisch verteidigen kann: „In diesem Fall interessieren wir uns nicht für Ausreißer, sie sind einfach nicht von Interesse“ oder „Das war der Tag, an dem Uncle Jerry eingekauft und mir 100 Dollar gekippt hat. Das ist nicht vorhersehbar, und es lohnt sich nicht, in das Modell aufzunehmen.“
Verbessern Ihres Modells: Variablen transformieren
Übersicht
Die häufigste Methode zur Verbesserung eines Modells ist die Transformation einer oder mehrerer Variablen, in der Regel mithilfe einer „Protokoll“-Transformation.
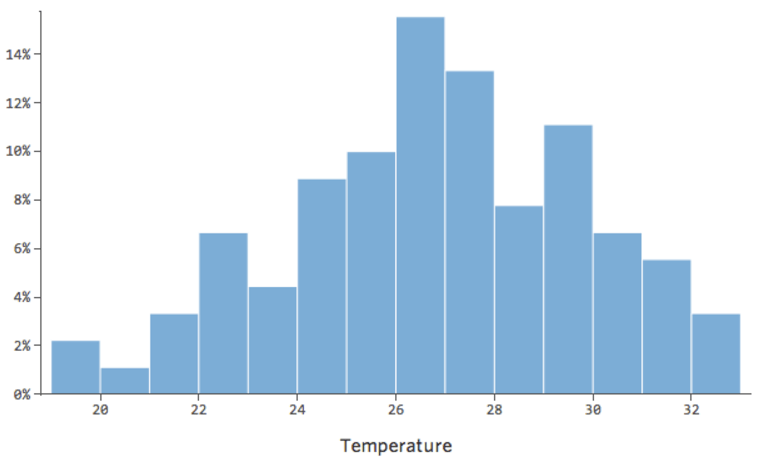
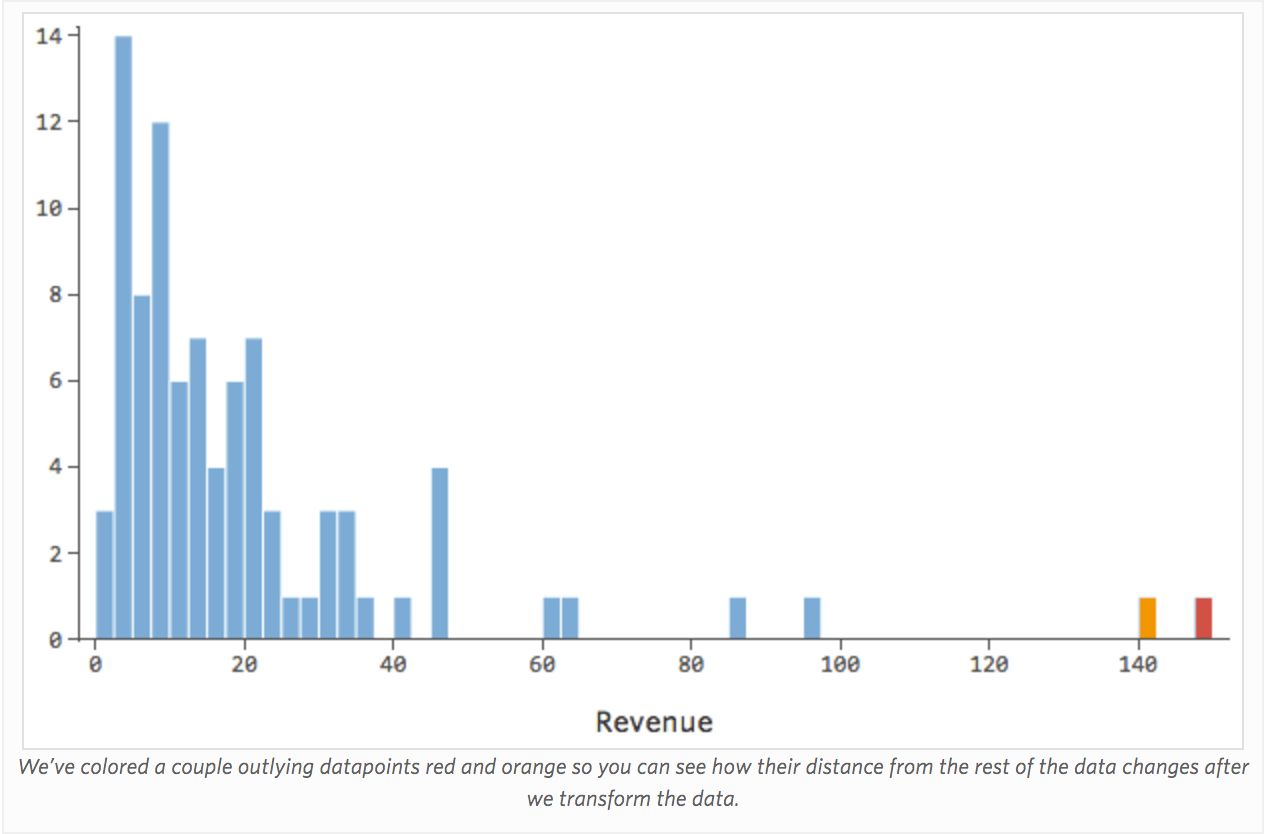
Das Transformieren einer Variable ändert die Form ihrer Verteilung. In der Regel ist der beste Startort eine Variable mit einer asymmetrischen Verteilung im Gegensatz zu einer symmetrischen oder glockenförmigeren Verteilung. Suchen Sie eine Variable wie die folgende, um sie zu transformieren:
Im Allgemeinen funktionieren Regressionsmodelle besser mit symmetrischen, glockenförmigen Kurven. Probieren Sie verschiedene Arten von Transformationen aus, bis Sie auf diejenige stoßen, die dieser Form am nächsten kommt. Oft ist es nicht möglich, sich dem anzunähern, aber das ist das Ziel. Angenommen, Sie verwenden die Quadratwurzel von „Umsatz“ als Versuch, eine symmetrischere Form zu erreichen, und Ihre Verteilung sieht wie folgt aus:
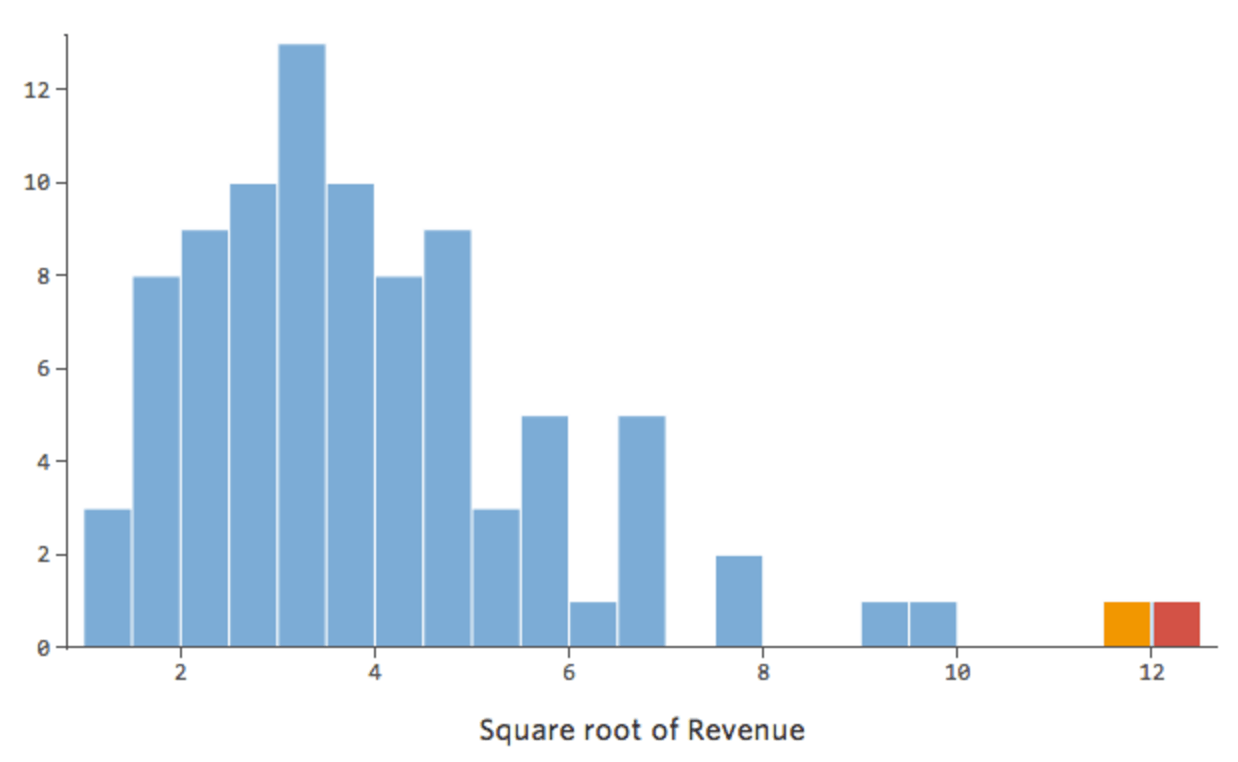
Das ist gut, aber noch ein bisschen asymmetrisch. Lassen Sie uns versuchen, stattdessen das Erlösprotokoll zu verwenden, das folgende Form ergibt:
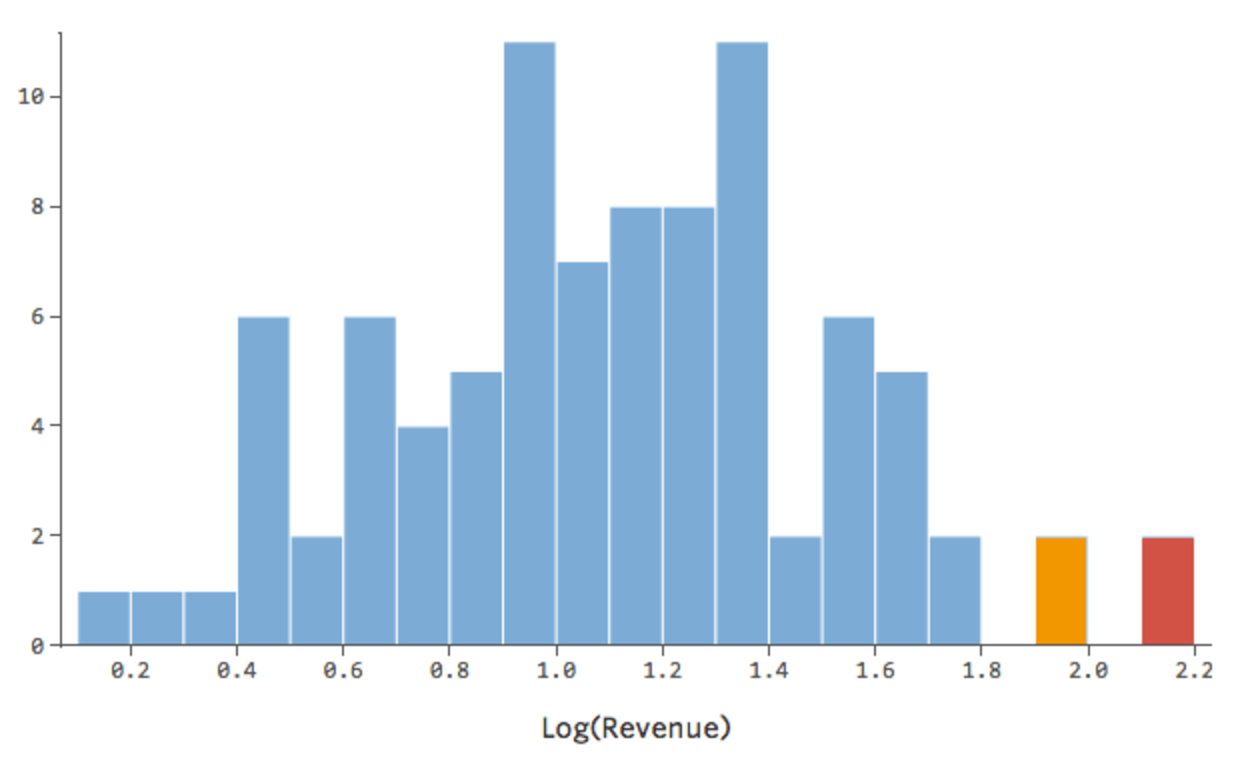
Das ist nett und symmetrisch. Sie werden wahrscheinlich ein besseres Regressionsmodell mit log(„Umsatz“) anstelle von „Umsatz“ erhalten. So können sich Ihre Gleichung, Ihre Residuen und Ihr R-Quadrat ändern:
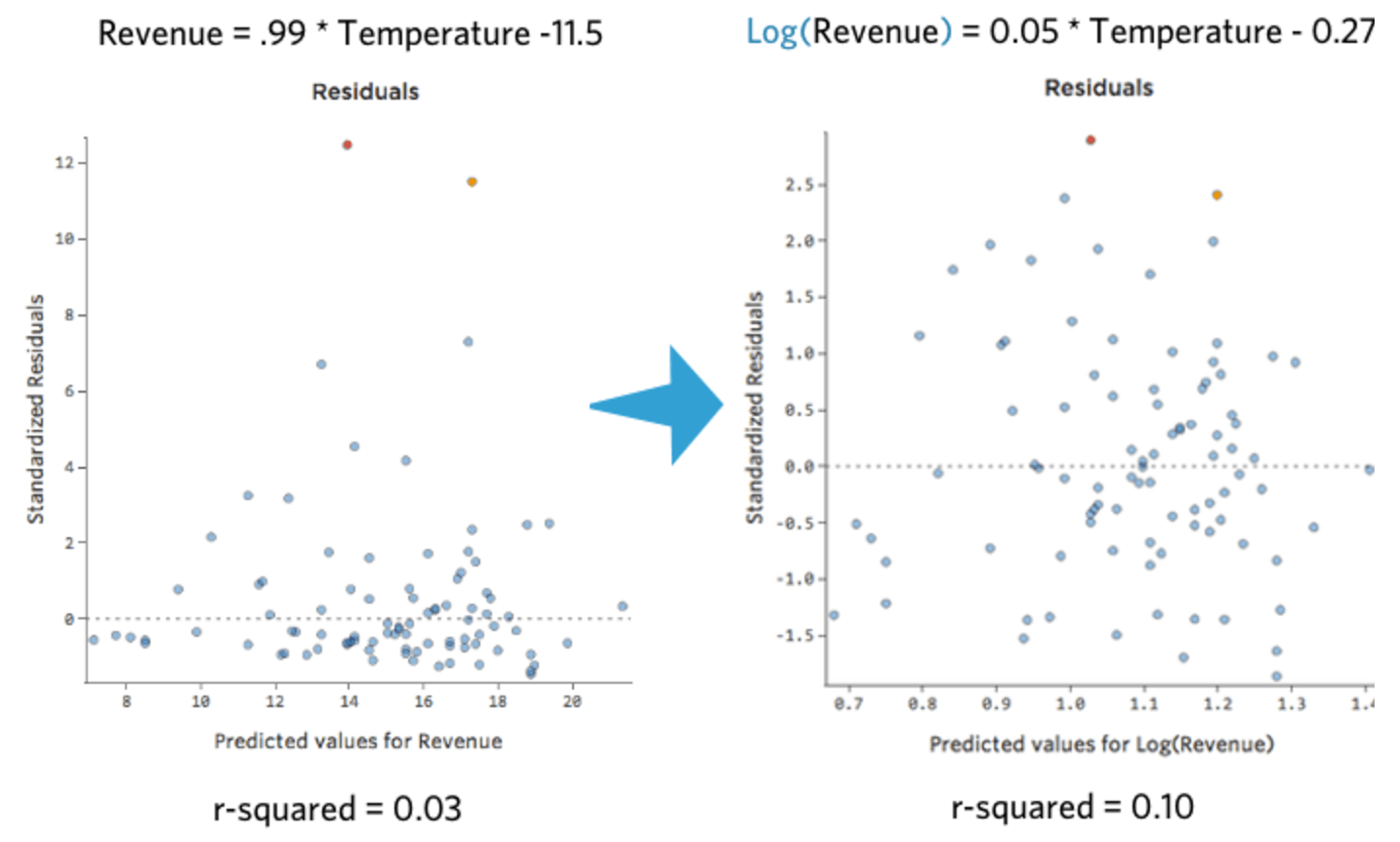
Stats iQ zeigt eine kleine Version der Verteilung der Variablen inline mit der Regressionsgleichung an: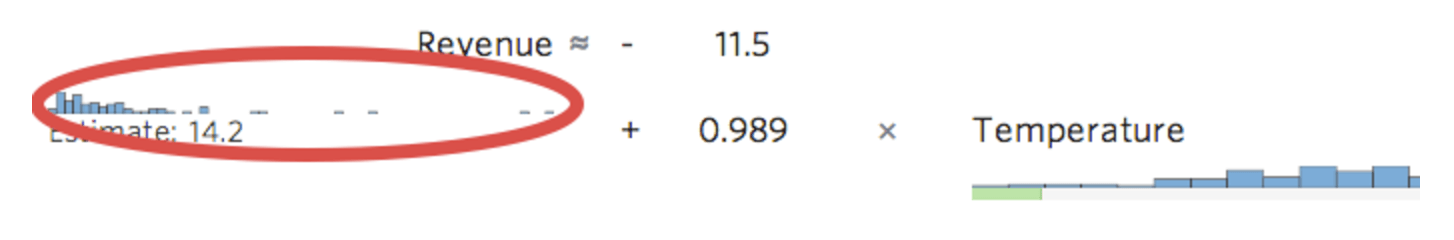
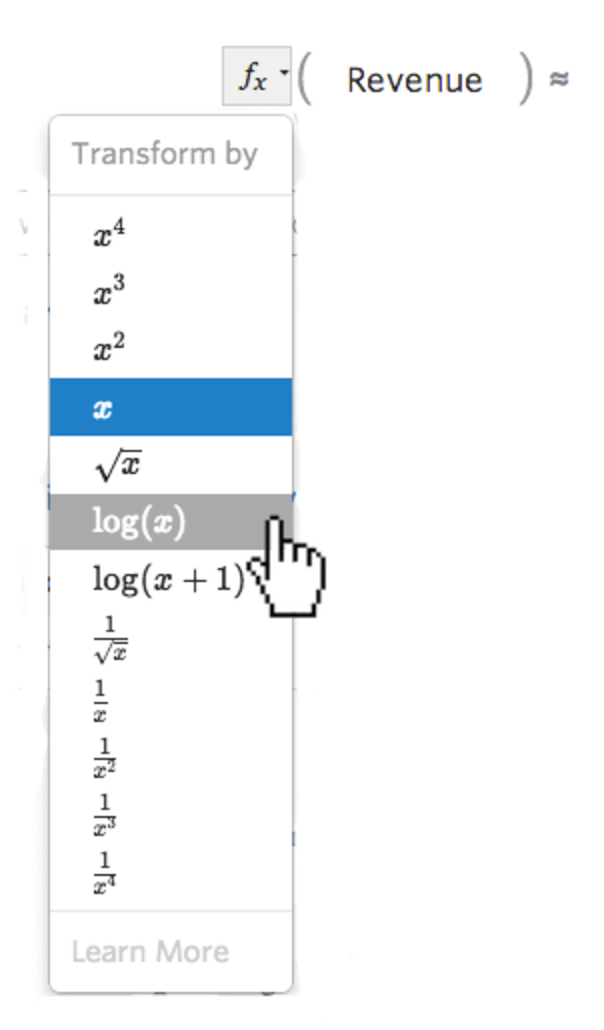
Wählen Sie die Drucktaste fx der Transformation links neben der Variable …
… dann eine Transformation auswählen, meistens log(x)...
… prüfen Sie dann das Histogramm, um herauszufinden, ob es zentrierter ist, da dieses nach der Transformation angezeigt wird:

Nachdem Sie eine Variable transformiert haben, beachten Sie, wie sich ihre Verteilung, das R-Quadrat der Regression und die Muster des Restplots ändern. Wenn sich diese verbessern (insbesondere das R-Quadrat und die Residuen), ist es wahrscheinlich am besten, die Transformation beizubehalten.
Wenn eine Transformation erforderlich ist, sollten Sie zunächst eine „Protokoll“-Transformation durchführen, da die Ergebnisse Ihres Modells noch leicht verständlich sein werden. Beachten Sie jedoch, dass Probleme auftreten, wenn die Daten, die Sie zu transformieren versuchen, Nullen oder negative Werte enthalten. Wenn Sie erfahren möchten, warum das Erstellen eines Protokolls so nützlich ist oder wenn Sie nicht positive Zahlen transformieren möchten oder nur ein besseres Verständnis darüber erhalten möchten, was bei der Transformation von Daten passiert, lesen Sie die Details unten.
Details
Wenn Sie die log10() einer Zahl nehmen, sagen Sie „10 zu welcher Kraft gibt mir diese Zahl“. Im Folgenden finden Sie beispielsweise eine einfache Tabelle mit vier Datenpunkten, die sowohl „Umsatz“ als auch log(„Umsatz“) enthält:
| Temperatur | Umsatz | log(Umsatz) |
|---|---|---|
| 20 | 100 | 2 |
| 30 | 1.000 | 3 |
| 40 | 10.000 | 4 |
| 45 | 31.623 | 4,5 |
Beachten Sie, dass wenn wir „Temperatur“ vs. „Umsatz“ und „Temperatur“ vs. log(„Umsatz“), das letztere Modell passt viel besser.
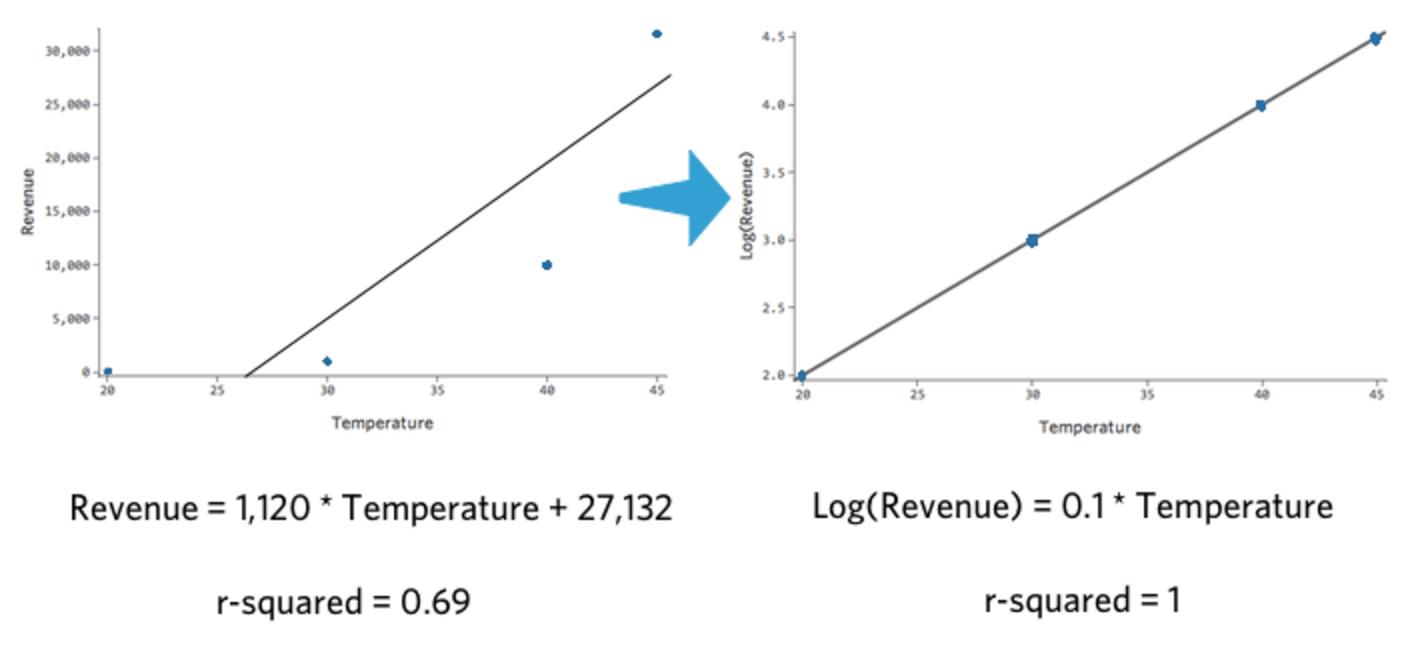
Das Interessante an dieser Transformation ist, dass Ihre Regression nicht mehr linear ist. Als „Temperatur“ von 20 auf 30 ging, ging „Umsatz“ von 10 auf 100, eine 90-Einheiten-Lücke. Als dann „Temperatur“ von 30 auf 40 ging, ging „Umsatz“ von 100 auf 1000, eine deutlich größere Lücke.
Wenn Sie ein Protokoll Ihrer Antwortvariablen erstellt haben, ist es nicht mehr der Fall, dass eine Erhöhung der „Temperatur“ um eine Einheit eine Erhöhung des „Umsatzes“ bedeutet. Jetzt ist es ein X-Prozent-Plus bei „Umsatz“. In diesem Fall ist ein zehnstufiger Anstieg der „Temperatur“ mit einem Anstieg von 1000 % an Y verbunden, d.h. ein Anstieg der „Temperatur“ um eine Einheit ist mit einem Anstieg des „Umsatzes“ um 26 % verbunden.
Beachten Sie auch, dass Sie das Protokoll von 0 oder einer negativen Zahl nicht verwenden können (es gibt kein X, wobei 10X = 0 oder 10X= -5 ist). Wenn Sie also eine Protokolltransformation durchführen, gehen diese Datenpunkte aus der Regression verloren. Es gibt vier häufige Möglichkeiten, mit der Situation umzugehen:
- Verwenden Sie eine Quadratwurzel oder eine Würfelwurzel. Diese werden die Form der Kurve nicht so dramatisch verändern wie ein Protokoll, aber sie ermöglichen es, dass Nullen in der Regression verbleiben.
- Wenn nicht zu viele Datenzeilen eine Null haben und diese Zeilen theoretisch nicht wichtig sind, können Sie mit dem Protokoll fortfahren und einige Zeilen aus Ihrer Regression verlieren.
- Anstatt log(y) zu verwenden, verwenden Sie log(y+1), sodass Nullen zu eins werden und dann in der Regression beibehalten werden können. Dies verfälscht Ihr Modell ein bisschen und ist etwas verblüfft, aber in der Praxis sind seine negativen Nebenwirkungen in der Regel ziemlich gering.
Verbessern Ihres Modells: Fehlende Variablen
Der häufigste Grund dafür, dass ein Modell nicht passt, ist, dass nicht alle richtigen Variablen enthalten sind. Für dieses spezielle Problem gibt es viele mögliche Lösungen.
Neue Variable hinzufügen
Manchmal ist die Korrektur so einfach wie das Hinzufügen einer weiteren Variable zum Modell. Wenn beispielsweise der Verkehr bei Limonaden-„Umsatz“ an Wochenenden viel größer war als Wochentage, könnte Ihr vorhergesagter vs. tatsächlicher Plot wie folgt aussehen (R-Quadrat 0,053), da das Modell nur den Durchschnitt der Wochenendtage und Wochentage annimmt:
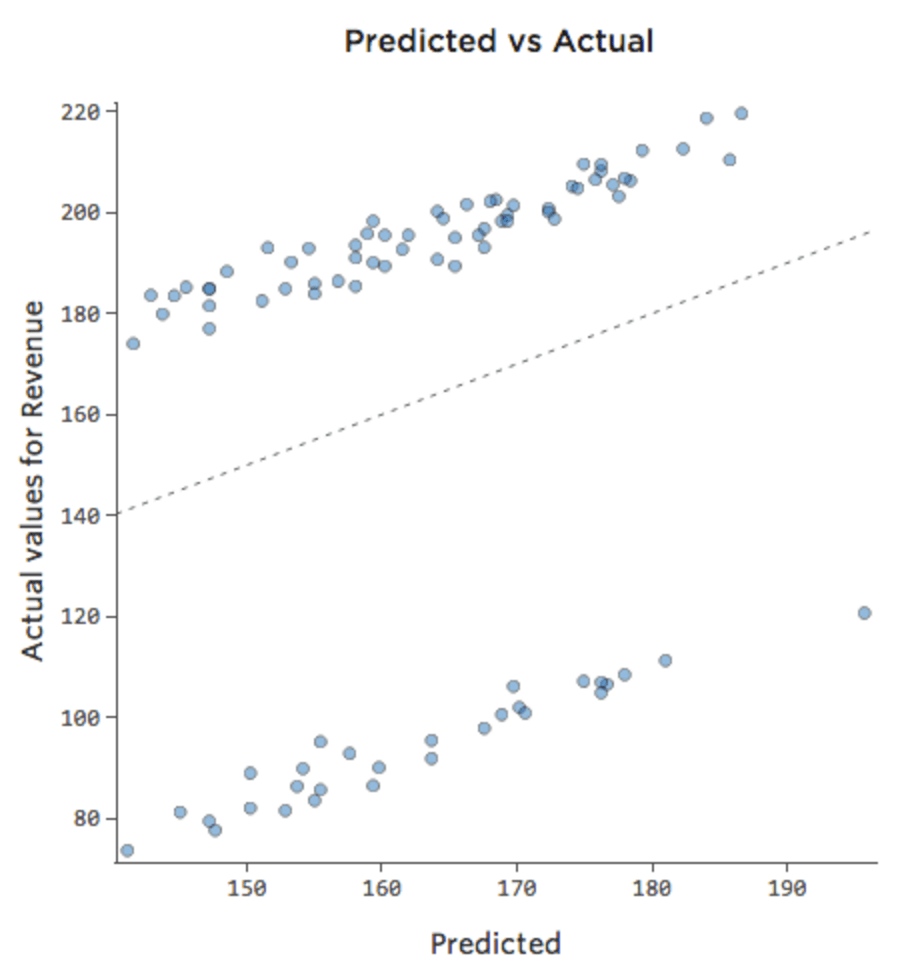
Wenn das Modell eine Variable namens „Wochenende“ enthält, könnte der prognostizierte vs. tatsächliche Plot wie folgt aussehen (R-Quadrat von 0,974):
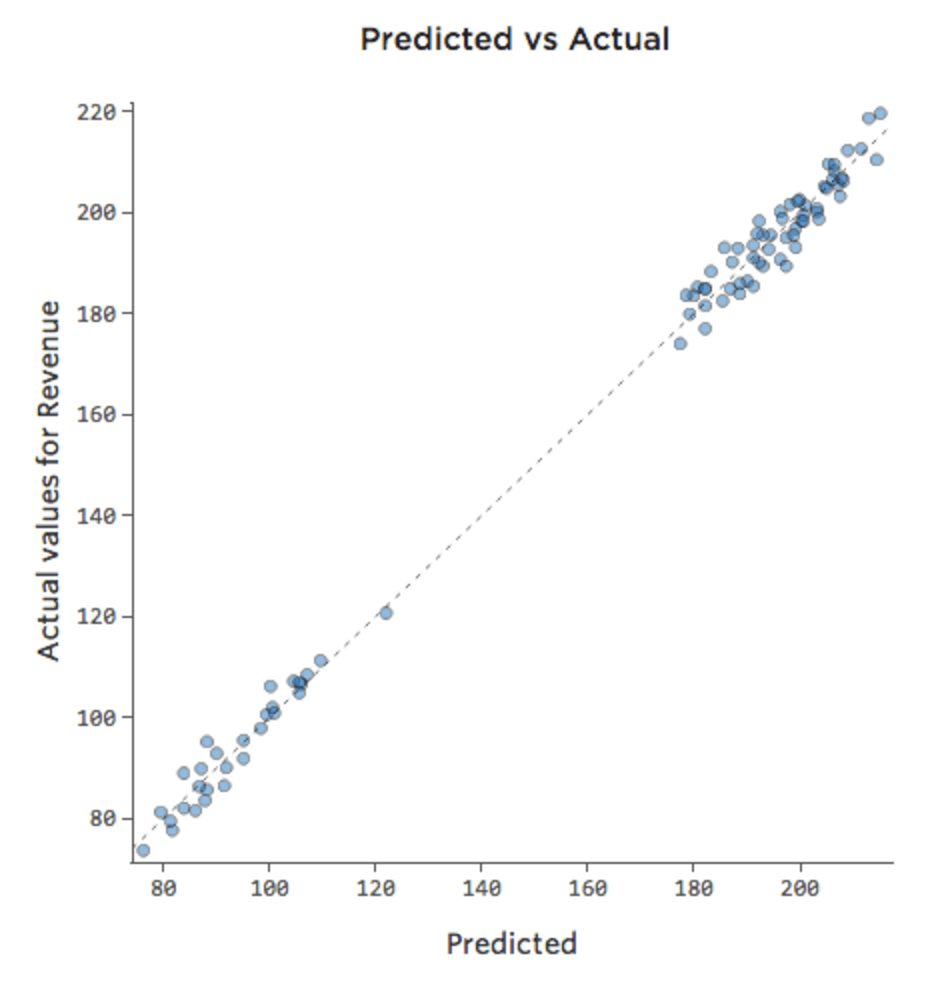
Das Modell erstellt weitaus genauere Prognosen, da es berücksichtigen kann, ob ein Wochentag ein Wochentag ist oder nicht.
Beachten Sie, dass Sie manchmal Variablen in Stats iQ anlegen müssen, um Ihr Modell auf diese Weise zu verbessern. Beispiel: Sie haben eine Datumsvariable (mit Werten wie „26.10.2014“) und müssen unter Umständen eine neue Variable mit der Bezeichnung „Wochentag“ (d. h. Sonntag) oder „Wochenende“ (d. h. Wochenende) anlegen.
Nicht verfügbare ausgelassene Variable
Selten ist es aber so einfach. Häufig ist die relevante Variable nicht verfügbar, da Sie nicht wissen, was sie ist oder schwer zu sammeln war. Vielleicht war es kein Wochenend- vs. Wochentagsproblem, sondern so etwas wie „Anzahl der Mitbewerber in der Gegend“, das du damals nicht sammeln konntest.
Wenn die benötigte Variable nicht verfügbar ist oder Sie gar nicht wissen, was sie sein würde, kann Ihr Modell nicht wirklich verbessert werden, und Sie müssen es bewerten und entscheiden, wie zufrieden Sie damit sind (ob es nützlich ist oder nicht, obwohl es fehlerhaft ist).
Interaktionen zwischen Variablen
Vielleicht verkauft sich an Wochenenden der Limonadenstand immer mit 100 Prozent Kapazität, also unabhängig von der „Temperatur“ ist „Umsatz“ hoch. Doch an Wochentagen ist der Limonadenstand deutlich weniger beschäftigt, so dass „Temperatur“ ein wichtiger Treiber von „Umsatz“ ist. Wenn Sie eine Regression ausgeführt haben, die „Wochenende“ und „Temperatur“ enthielt, sehen Sie möglicherweise einen prognostizierten vs. tatsächlichen Graphen wie diesen, wobei die Zeile oben die Wochenendtage sind.
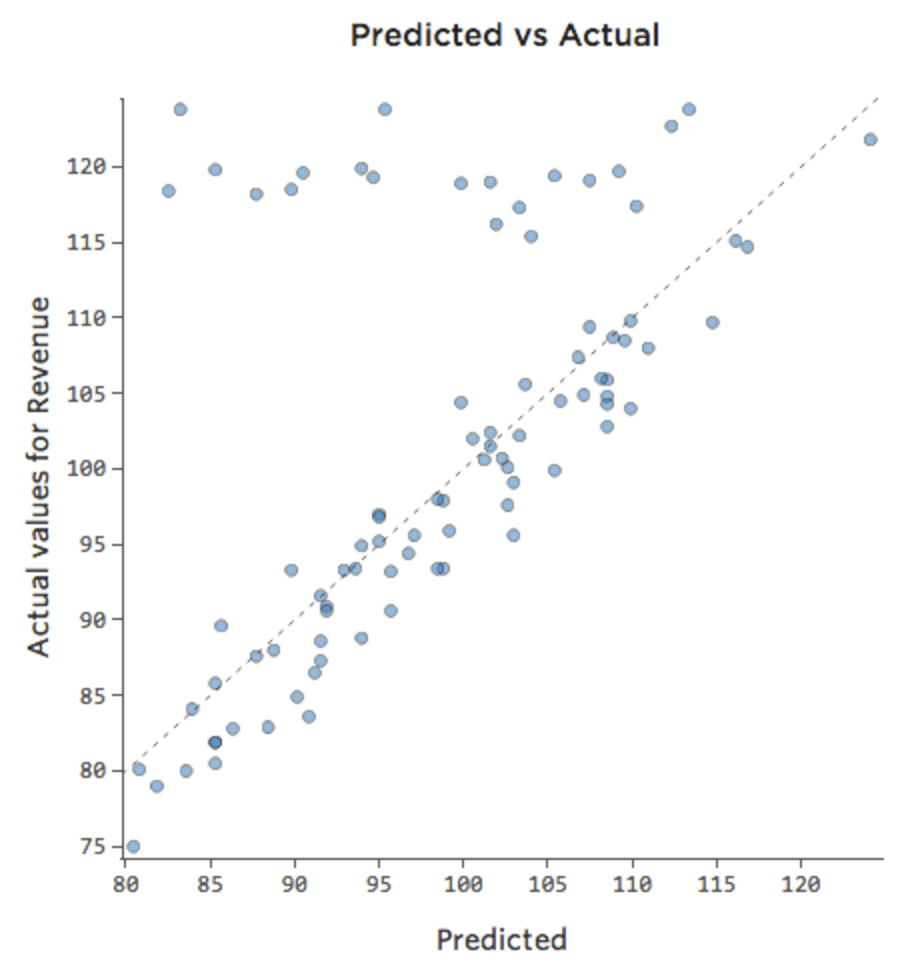
Wir würden sagen, dass es eine Interaktion zwischen „Wochenende“ und „Temperatur“ gibt; die Auswirkung einer von ihnen auf „Umsatz“ ist je nach Wert der anderen unterschiedlich. Wenn wir eine Interaktionsvariable anlegen, erhalten wir ein wesentlich besseres Modell, bei dem prognostiziert vs. tatsächlich wie folgt aussieht:
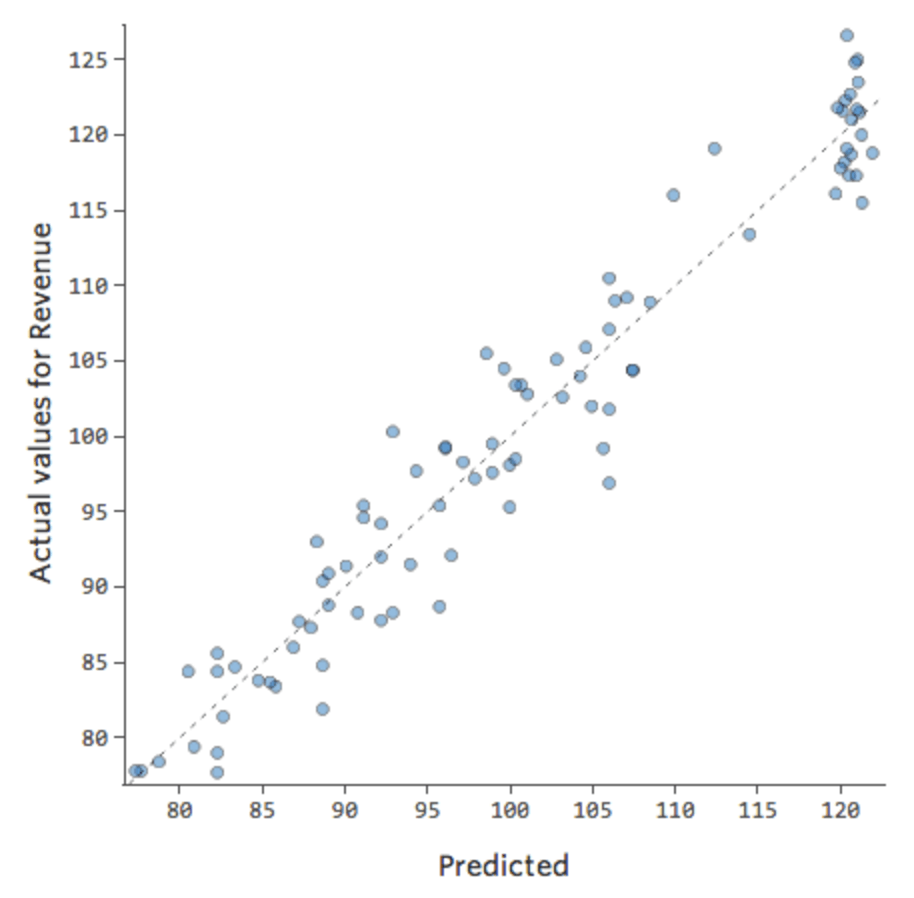
Verbessern Sie Ihr Modell: Unlinearität beheben
Angenommen, Sie haben eine Beziehung, die wie folgt aussieht:
Sie stellen unter Umständen fest, dass die Form einer Parabolie, die Sie möglicherweise zurückrufen, typischerweise mit Formeln verknüpft ist, die wie folgt aussehen:
y = x2 + x + 1
Standardmäßig verwendet die Regression ein lineares Modell, das wie folgt aussieht:
y = x + 1
Tatsächlich hat die Linie in der obigen Grafik folgende Formel:
y = 1,7x + 51
Aber es ist keine gute Anpassung. Wenn wir also x2 hinzufügen, hat unser Modell eine bessere Chance, die Kurve anzupassen. Tatsächlich legt sie Folgendes an:
Die Formel für diese Kurve lautet:
y = –2×2 +111x – 1408
Das bedeutet, dass sich unsere Diagnosediagramme von dieser …
… dazu:
Beachten Sie, dass es sich hierbei um gesunde Diagnosediagramme handelt, auch wenn die Daten auf der rechten Seite unausgewogen erscheinen.
Der obige Ansatz kann durch Hinzufügen von x3 auf andere Formen, insbesondere eine S-förmige Kurve, ausgedehnt werden. Das ist aber relativ selten.
Vorsicht:
- Wenn Sie aufgrund eines nicht linearen Musters in Ihren Daten einen x2-Begriff haben, möchten Sie im Allgemeinen einen guten alten x-Begriff haben. Ihr Modell ist vielleicht vollkommen gut ohne es, aber Sie sollten auf jeden Fall versuchen, beides zu starten.
- Die Regressionsgleichung kann schwer verständlich sein. Für die lineare Gleichung zu Beginn dieses Abschnitts ging für jede zusätzliche Einheit von „Temperatur“ „Umsatz“ um 1,7 Einheiten hoch. Wenn Sie sowohl x2 als auch x in der Gleichung haben, ist es nicht einfach zu sagen: „Wenn die Temperatur um einen Grad ansteigt, passiert das.“ Manchmal ist es aus diesem Grund einfacher, einfach eine lineare Gleichung zu verwenden, vorausgesetzt, dass die Gleichung gut genug passt.