Die Verwechslungsmatrix und der Precision-Recall Tradeoff

Konfusionsmatrix

Angenommen, Sie überlegen, Kunden, die wahrscheinlich zurückkehren werden, einen zusätzlichen Zuckerwürfel zu geben. Aber natürlich möchten Sie vermeiden, dass Zuckerwürfel unnötig verschenkt werden, also geben Sie sie nur an Kunden, die laut Modell mindestens 30 % zurückgeben werden.

Wenn Sie neue Kunden haben …

…Sie können unser Regressionsmodell verwenden, um vorherzusagen, wie wahrscheinlich es wäre, dass sie zurückkehren…

…und beschließen Sie, Kunden mit einer Wahrscheinlichkeit von mindestens 30 % als “Wird zurückgeben” zu klassifizieren und ihnen Zuckerwürfel zu geben:

Um jedoch besser zu verstehen, wie genau unser Modell ist, können Sie das Modell auf die Datenpunkte anwenden, die Sie bereits haben, wo Sie bereits wissen, ob der Kunde letztendlich zurückgekommen ist…

…und beurteilen Sie, wie genau die Daten sind…

…und dann weiter aufschlüsseln in die folgenden Kategorien:

• Richtig positiv: Vom Modell als “Will return” klassifiziert und hatte tatsächlich “Returned” in Wirklichkeit.
• Falsch positiv: Wird vom Modell als „Wird zurückgeben“ klassifiziert, aber eigentlich „Nicht zurückgekehrt“ in Wirklichkeit.
• True Negativ: Klassifiziert vom Modell als „Won’t return“ und in Wirklichkeit als „Didn’t return“.
• False Negativ: Wird vom Modell als „Gewonnen, nicht zurückgegeben“ klassifiziert, hatte aber tatsächlich „Zurückgegeben“.

Schließlich könnten Sie all diese Arbeiten in Präzision und Rückruf zusammenfassen.

Genauigkeit:

• Welcher Anteil von denen, die als “Wird zurückkehren” eingestuft sind, hat tatsächlich geholfen?
• Wahr positiv / (wahr positiv + falsch positiv)

Rückruf:

• Rückruf: Von denen, die eigentlich “zurückgekehrt” sind, welcher Anteil wurde so eingestuft?
• Wahr positiv / (wahr positiv + falsch negativ)

Bessere Modelle haben höhere Werte für Präzision und Rückruf.

• Man kann sich ein Modell mit 94% Präzision (fast alle als “Will return” tun eigentlich) und 97% Rückruf (fast alle, die “Returned” als solche identifiziert haben) vorstellen.
• Ein schwächeres Modell könnte 95 % Genauigkeit haben, aber 50 % Rückruf (wenn es jemanden als „Will return“ identifiziert, ist es weitgehend korrekt, aber es wird als „Won’t return“ die Hälfte derjenigen genannt, die tatsächlich später „Return“ getan haben).
• Oder vielleicht hat das Modell 60% Präzision und 60% Recall.

Diese Zahlen sollten Ihnen einen guten Überblick darüber geben, wie genau Ihr Modell ist, auch wenn Sie nie Prognosen erstellen möchten.

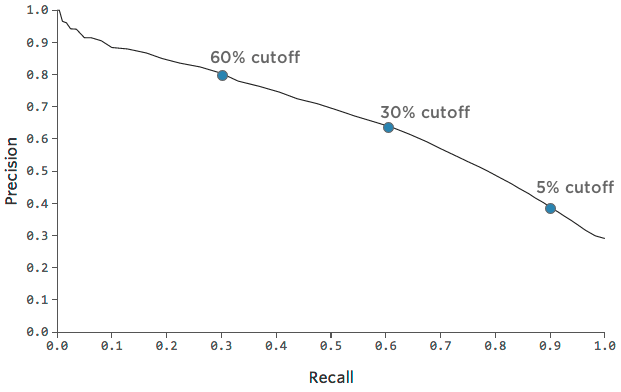
Genauigkeit vs. Rückrufkurve

Innerhalb eines Modells können Sie auch die Präzision oder den Rückruf hervorheben. Vielleicht sind Sie bei Zuckerwürfeln sehr kurz und möchten sie nur an Personen weitergeben, von denen Sie sehr zuversichtlich sind, dass sie zurückkehren werden. Daher entscheiden Sie sich, sie nur Kunden zu geben, die 60 % wahrscheinlich zurückgeben (statt 30 %).

Unsere Präzision wird steigen, denn Sie geben nur Zuckerwürfel aus, wenn Sie wirklich zuversichtlich sind, dass jemand „Werden zurückkehren“. Unser Rückruf wird zurückgehen, denn es wird viele Leute geben, die letztendlich “zurückkehren”, denen Sie nicht sicher genug waren, einen Zuckerwürfel zu geben.

Präzision:   62%   —>   80%
Recall:        60%   —>   30%

Oder wenn Sie sich reich an Zuckerwürfeln fühlen, könnten Sie sie jedem geben, der mindestens 10% Chance hat, ein Rückkehrer zu sein.

Genauigkeit:   62%   —>   40%
Recall:        60%   —>   90%

Mit diesem Diagramm können Sie diesen Kompromiss zwischen Präzision und Rückruf nachvollziehen:

Es kann hilfreich sein, einen Punkt im Diagramm auszuwählen, der eine schöne Mischung aus Präzision und Rückruf darstellt, und dann ein Gefühl dafür zu gewinnen, wie genau das Modell an diesem Punkt ist.

Häufig gestellte Fragen