Vorgefertigte R-Skripte

Über vorkomponierte R-Skripte

R ist eine statistische Programmiersprache, die häufig für flexible und leistungsstarke Analysen verwendet wird. Wenn Sie R-Coding in Stats iQ verwenden, können Sie aus mehreren Analyseskripten auswählen, um die Verwendung von R einfacher und effizienter zu gestalten.

Skript für R-Code auswählen

1. Wählen Sie aus, welche Variablen Sie analysieren möchten. Weitere Informationen finden Sie unter Dataframe-Variablen für R-Code auswählen.
   
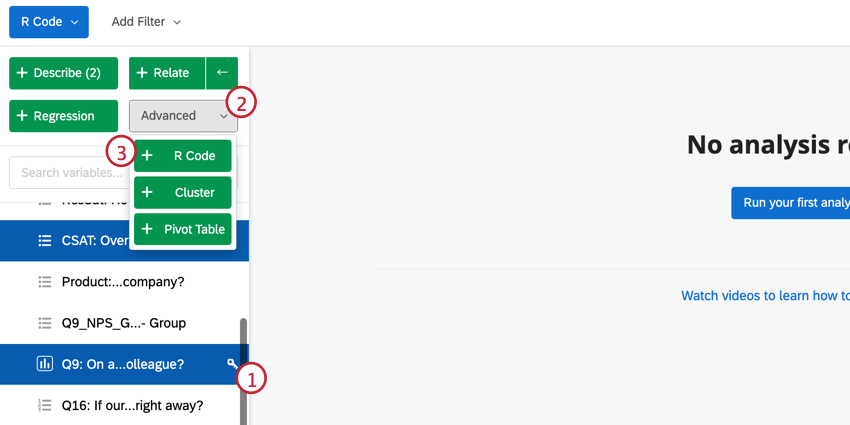
2. Klicken Sie auf Erweitert.
3. Klicken Sie auf R-Code.
4. Wählen Sie ein Skript aus. Weitere Informationen zu den Analysemöglichkeiten finden Sie in den nachfolgenden Abschnitten.
   
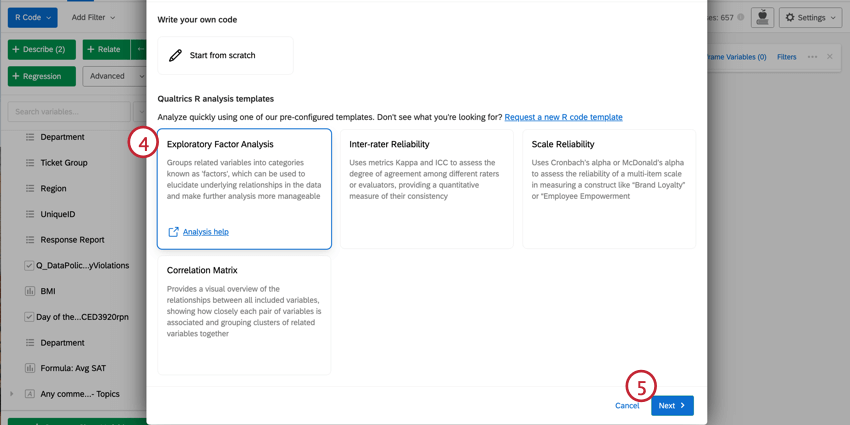
5. Klicken Sie auf Weiter.
6. Bestätigen Sie die ausgewählten Variablen. Wenn Sie eine Variable ändern möchten, klicken Sie auf die Dropdown-Liste, und wählen Sie eine neue aus.
   
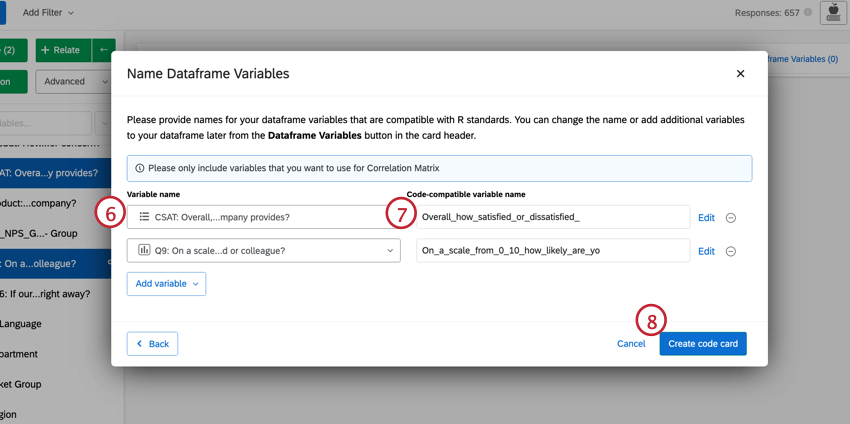
7. Bearbeiten Sie bei Bedarf den Namen für Ihre Variablen. Weitere Informationen finden Sie unter Dataframe-Variablen für R-Code benennen.
   Tipp: Sie können direkt in diesem Fenster Änderungen an den ausgewählten Variablen vornehmen. Um die Umkodierungswerte zu bearbeiten, klicken Sie auf Bearbeiten. Wenn Sie die Variable löschen möchten, klicken Sie auf das Symbol ( – ). Wenn Sie eine neue Variable hinzufügen möchten, klicken Sie unten links auf Variable hinzufügen.
   
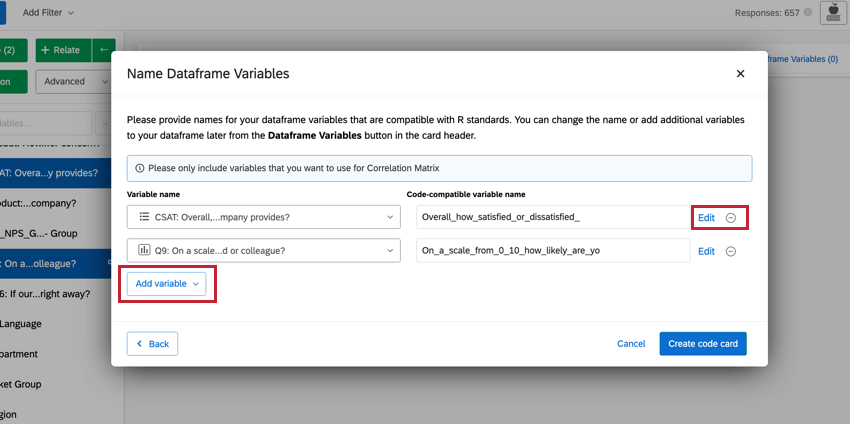
8. Wenn Sie mit der Bearbeitung Ihrer Dataframe-Variablen fertig sind, klicken Sie auf Codekarte erstellen.

Navigieren durch vorkomponierte R-Code-Skripte

Ihr Skript wird in den Code-Abschnitt der R-Code-Karte eingefügt. Dieser Code enthält Hinweise zusammen mit den Befehlen zum Generieren der ausgewählten Analyse. Um Ihre Analyse auszuführen, wählen Sie Alle ausführen. Die Ergebnisse werden im Ausgabefeld auf der rechten Seite angezeigt.

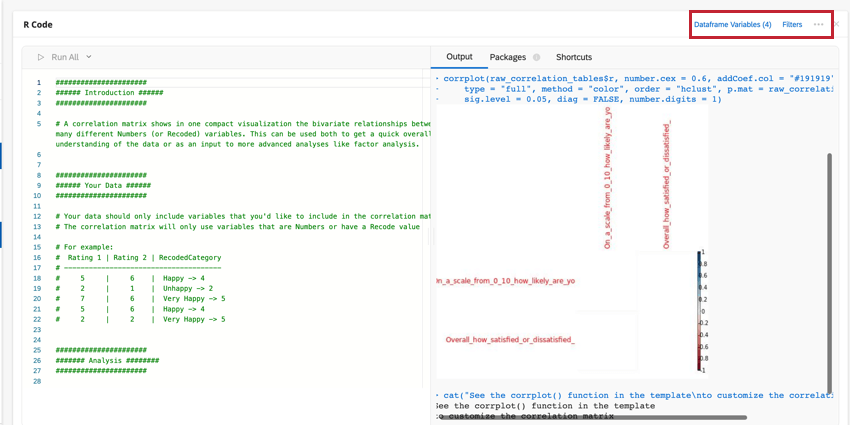
Sie können Ihre Dataframe-Variablen bearbeiten oder der Analyse einen Filter hinzufügen, indem Sie oben rechts auf die Optionen klicken. Klicken Sie auf das Drei-Punkt-Menü, um Ihrer Codekarte Notizen hinzuzufügen, die Analyse zu kopieren oder die Karte im Vollbild zu öffnen.

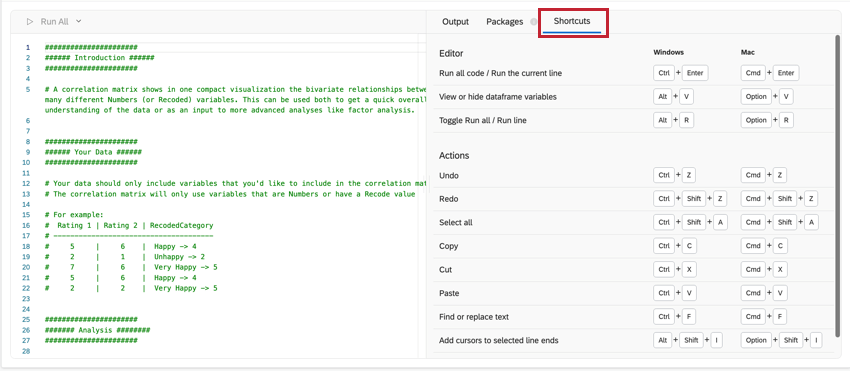
SHORTCUTS

Tastenkombinationen können verwendet werden, um die R-Code-Karte effizienter zu navigieren. Klicken Sie auf Tastaturbefehle, um eine Liste der möglichen Aktionen anzuzeigen.

PACKAGES

R-Coding in Stats iQ wird vorinstalliert mit Hunderten der beliebtesten R-Pakete, die für die Analyse verwendet werden. Klicken Sie auf die Registerkarte Pakete in der rechten Hälfte der Karte, um die Liste der verfügbaren Pakete anzuzeigen. Weitere Informationen zur Verwendung von Paketen finden Sie unter R Coding in Stats iQ.

Zuverlässigkeit der Skala

Die Skalenzuverlässigkeit bewertet, inwieweit Positionen in einer Mehrpositionsskala ein Konstrukt zuverlässig messen können. Mit anderen Worten: Wenn dieselbe Sache mit demselben Fragensatz gemessen wird, gibt es verlässlich ähnliche Ergebnisse? Wenn dies der Fall ist, besteht die Zuversicht, dass alle Veränderungen, die wir in der Zukunft sehen, auf Veränderungen in der befragten Bevölkerung oder Interventionen zurückzuführen sind, die vorgenommen wurden, um die Punktzahl zu verbessern.

INTERPRETING RELIABILITY MASSNAHMEN

Die Messungen der Skalenzuverlässigkeit fallen zwischen 0 und 1 und stellen im Wesentlichen eine aggregierte Korrelation zwischen allen Positionen in der Skala dar.

Cronbachs Alpha, ein weit verbreitetes Zuverlässigkeitsmaß, unterschätzt die Zuverlässigkeit oft aufgrund bestimmter Annahmen. McDonald’s Omega, eine empfohlene Alternative, vermeidet diese Mängel. Wir verwenden standardmäßig McDonald’s Omega, aber Cronbachs Alpha wird immer noch allgemein akzeptiert.

Es gibt keine einzige korrekte Möglichkeit, die resultierende Zahl zu interpretieren, aber unsere bevorzugte Faustregel für beide Omegas ist unten beschrieben:

Wenn Ihre zuverlässige Skala nicht akzeptabel ist, gibt es einige Möglichkeiten, Ihren Datensatz zu beheben:

• Entfernen Sie alle Gegenstände, die Omega oder Alpha senken.
• Es ist möglich, dass zwei verschiedene Konstrukte gemessen werden. Wenn dies der Fall ist, würde das Trennen der Variablen in zwei Gruppen und das Ausführen dieser Analyse für jede dieser Gruppen zu Zuverlässigkeits-Scores führen, die höher sind als die der ersten Analyse. Sie können dies untersuchen, indem Sie die Korrelationsmatrix in der Ausgabe überprüfen oder das Skript Exploratory Factor Analysis verwenden, um zu sehen, welche Gruppierungen natürlich aus den Daten herausfallen.
• Letztendlich kann es erforderlich sein, die Umfrage erneut zu ändern und auszuführen. Positionen, die eine geringe Korrelation mit den anderen aufweisen, müssen möglicherweise geklärt oder nachbearbeitet werden, oder andere Positionen müssen hinzugefügt werden.

Sehr hohe Ergebnisse (z.B. 0,95) können auch auf ein Problem mit der Skala hinweisen, in der Regel, dass Sie noch eine Skala haben können, die sehr zuverlässig ist, ohne so viele Artikel zu haben. In diesem Fall empfehlen wir, die am wenigsten nützlichen Elemente aus der Skala zu entfernen und die Analyse erneut auszuführen.

INTERPRETING ITEM-LEVEL STATISTICS

Das Skript führt zunächst eine allgemeine Zuverlässigkeitsmessung aus und führt dann eine Iteration für jede Variable aus. Das Ziel der Analyse der Zuverlässigkeit pro Position ist es zu verstehen, welche Elemente für den Aufbau der Waage am nützlichsten sind. Stats iQ wird eine Tabelle ausgeben, die ähnlich aussieht:

Insgesamt McDonald’s Omega: 0.71

• Das allgemeine Ziel ist es, eine höhere McDonald’s Omega mit einer geringeren Anzahl von Gegenständen zu haben. Wenn also ein Forscher eine neue Skala erstellt, würde er A1 wahrscheinlich entfernen wollen, da das Omega tatsächlich höher ist, ohne es.
• Der Rest der Gegenstände, die die Zuverlässigkeit verringern würden, wenn sie entfernt würden, obliegt dem Forscher zu bestimmen. Wenn sich ein Forscher beispielsweise mit der Ermüdung von Umfragen beschäftigt, kann er eine größere Verringerung der Zuverlässigkeit bei der Entscheidung zulassen, eine Variable zu entfernen.
• Die Item-Total-Korrelation ist die Korrelation zwischen dieser Position und dem Durchschnitt aller anderen. Niedrige Item-Total-Korrelation deutet darauf hin, dass die Variable nicht repräsentativ genug für das zugrunde liegende Konstrukt ist. Die häufigste Faustregel ist, verdächtig zu sein für alles mit einer Item-Total-Korrelation von 0,3 oder niedriger, besonders wenn Sie viele Elemente haben, was die Zuverlässigkeitsmetrik künstlich aufbläht.

Wenn Sie ein Element entfernen möchten, sollten Sie alle anderen Statistiken erneut ausführen, bevor Sie entscheiden, ob ein anderes Element entfernt werden soll. In Stats iQ bedeutet dies, dass die Variable einfach von der gesamten Karte entfernt wird – der Rest erfolgt automatisch.

INTERPOSITIONSKORRELATIONSMATRIX

Die Interitem-Korrelationsmatrix zeigt die Korrelation zwischen den einzelnen Variablen in der Analyse und einander an. Wenn beispielsweise eine Variable sehr stark mit einer anderen korreliert (z. B. 0,9), können diese Fragen redundant sein, und das Entfernen der Variablen wirkt sich nur geringfügig auf Ihre Zuverlässigkeit aus.

Die durchschnittliche Korrelation zwischen Positionen ist der Durchschnitt der Zahlen in der Matrix. Höhere Zahlen deuten darauf hin, dass einige Positionen möglicherweise redundant sind und entfernt werden könnten. Generell sollten Variablen im Bereich von 0,2 bis 0,4 liegen.

MEHR RESSOURCEN

• Die Zuverlässigkeitsanalyse in Stats iQ wird von der Funktion compRelSem() aus dem Paket semTools R ausgeführt. Eine Vielzahl von erweiterten Einstellungen werden in der Dokumentation beschrieben. Es ist nicht erforderlich, diese Einstellungen zu verwenden oder zu verstehen, um eine Zuverlässigkeitsanalyse durchzuführen.
• Die Korrelationsmatrix wird von der corrplot-Funktion() aus dem corrplot-R-Paket ausgeführt. Eine Vielzahl von erweiterten Einstellungen und Anpassungen werden in der Dokumentation und in dieser Anleitung beschrieben.

Zuverlässigkeit zwischen Bewertern

Die Inter-Rater-Zuverlässigkeit (IRR) wird verwendet, um zu beurteilen, inwieweit zwei oder mehr Bewerter in ihrer Bewertung zustimmen. Beispielsweise könnten drei verschiedene Kodierer einen Textkommentar als positiv, neutral oder negativ bewerten; der IRR beschreibt, wie sehr sie miteinander einverstanden sind.

MASSNAHMEN DER INTERRATER RELIABILITÄT

Der IRR wird anhand leicht unterschiedlicher Metriken basierend auf der Struktur der Daten bewertet. Beispielsweise wird bei einer Analyse der Interzuverlässigkeit von zwei Bewertern eine etwas andere Metrik als bei der Interzuverlässigkeit von 3 Bewertern verwendet.

Stats iQ wählt automatisch die entsprechende Metrik für Ihre Daten aus.

INTERPRETING-ERGEBNISSE

Die Kappa- oder ICC-Metrik ist die Primärausbeute zwischen 0 und 1 und gibt an, wie gut die Rater korreliert sind. Wir schlagen die folgenden Bereiche für die Interpretation der Kappa vor:

MEHR RESSOURCEN

• Diese Zuverlässigkeitsanalyse wird von den Funktionen aus dem IRR R-Paket durchgeführt. Eine Vielzahl von erweiterten Einstellungen werden in der Dokumentation beschrieben. Es ist nicht erforderlich, diese Einstellungen zu verwenden oder zu verstehen, um diese Analyse auszuführen.

Explorative Faktorenanalyse

Die Explorationsfaktoranalyse (EFA) ist eine statistische Methode, mit der Sie eine große Anzahl von Variablen in einen kleineren, überschaubareren Satz zusammengefasster „Faktoren“ reduzieren können. Dies erleichtert die Interpretation, Kommunikation und weitere Analysen (z. B. Regressionsanalyse) erheblich. Die EFA folgt in der Regel dieser Reihe von Schritten:

1. Diagnose: Führen Sie eine Reihe von Diagnosen aus, die bestimmen, ob die Daten für die Faktoranalyse geeignet sind, und interpretieren Sie sie. Die Variablen müssen ausreichend miteinander korreliert sein, um sinnvolle Gruppierungen zu bilden, aber nicht so stark korreliert, dass sie im Wesentlichen redundant sind.
2. Auswahl der Faktoren: Bestimmen Sie die Anzahl der Faktoren, die in den Daten vorhanden sind. Faktoren sind die Gruppierungen ähnlicher Variablen zusammen. Standardmäßig verwendet das R-Skript ein Kriterium, das automatisch berechnet und ausgeführt wird.
3. Benennungsfaktoren: Nach der Ausführung der EFA bleiben Ihnen mehrere Faktoren übrig, die die wichtigsten Themen in den Daten am besten darstellen. Es ist hilfreich, diese Faktoren mit visuell lesbaren Namen zu kennzeichnen, die ihre Bedeutung festhalten.
4. Zugehörige Kennzahlen & Metriken: Die Faktoranalyse wird mit der Anzahl der Faktoren aus dem vorherigen Schritt ausgeführt. Das Ergebnis ist eine Reihe von Gruppierungen von Variablen zusammen mit einer statistischen Beschreibung der Aliquotierung.

Das Ergebnis ist ein Satz benannter Faktoren und ihrer Komponentenumfrageelemente. Diese Faktoren können als konzeptioneller Rahmen für weitere Analysen dienen oder zurück auf die Daten angewendet werden.

DIAGNOSTIK

Das Skript führt zunächst eine Reihe von Diagnosen aus, um sicherzustellen, dass die Daten für die EFA geeignet sind:

• Stichprobengröße: Im Allgemeinen wird ein 10:1-Verhältnis von Antworten zu Artikeln vorgeschlagen. Wenn Sie beispielsweise 10 Fragen haben, sollten Sie mindestens 100 Teilnehmer haben.
• Bartlett’s Test of Sphericity: Dieser Test bewertet, ob die Items so korreliert sind, dass sie sinnvoll in Faktoren gruppiert werden können. Wenn dies fehlschlägt, gibt es wahrscheinlich mehrere Positionen, die nicht ausreichend mit den anderen korrelieren. Sie können Elemente aus Ihrer Analyse entfernen, die nicht mit anderen korrelieren, oder der Umfrage weitere zugehörige Elemente hinzufügen.
• Determinante: Die Determinante bewertet, ob die Positionen zu stark korreliert sind, um sinnvoll in Faktoren gruppiert zu werden. Wenn diese Diagnose fehlschlägt, gibt es wahrscheinlich Elemente, die einander zu ähnlich sind, um sich in Faktoren zu unterteilen. Ziehen Sie die Bearbeitung von Umfrageelementen in Betracht, um deutlicher zu sein.
• Maßnahme Kaiser-Meyer-Olkin (KMO): Diese Kennzahl prüft, ob Ihre Umfrageelemente genug Gemeinsamkeiten haben, um sie in aussagekräftige Faktoren zu gruppieren. Wenn Sie diese Diagnose bestanden haben, haben die Antworten in Ihrer Umfrage viele Gemeinsamkeiten und können gut gruppiert werden. Andernfalls gruppieren die Elemente nicht in Kategorien. Wenn diese Diagnose fehlschlägt, können Sie Ihre Umfrageelemente überarbeiten, um ähnliche Themen zu erfassen und Elemente zu entfernen, die keine eindeutige Beziehung zu anderen aufweisen.

CHOOSING-FAKTOREN

Der Zweck der EFA besteht darin, viele Variablen in eine relativ kleine Anzahl zu kochen, die für die Analyse nützlich sind. Daher müssen Sie die Faktoranalyse möglicherweise mehrmals mit einer unterschiedlichen Anzahl von Faktoren ausführen, um eine Gruppierung zu finden, die für Sie funktioniert. Das EFA-Skript wird die Anzahl der Faktoren durch die Verwendung ihrer Eigenwerte vorschlagen.

Das EFA-Skript gibt ein Bildschirmdiagramm aus, das die Eigenwerte der Variablen in absteigender Reihenfolge anzeigt. Sie können das Diagramm untersuchen, um zu sehen, wie viele Faktoren vor dem „Ellbogen“ im Diagramm auftreten. Danach ist das Hinzufügen weiterer Faktoren weniger hilfreich.

Beispiel: In diesem Beispiel gibt es eine große Abladung nach der 4. Variablen und dann eine weitere signifikante Abgabe nach der 5. Variablen. Standardmäßig verwendet das Skript hier 5 Faktoren, aber Sie können es auch mit vier Faktoren ausführen und Ihre Ergebnisse vergleichen.

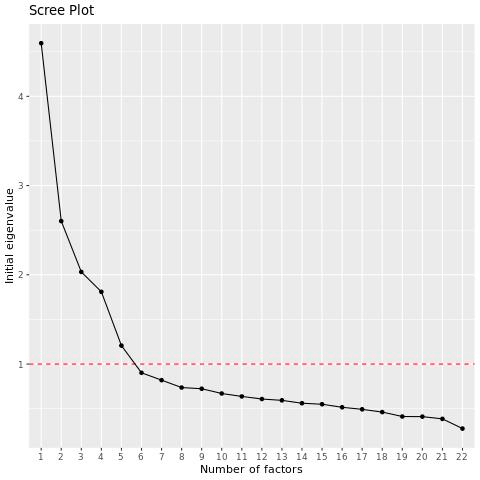
NAMIEREN SIE IHRE FAKTOREN

Nach der Ausführung der EFA wird jede Variable einem Faktor zugeordnet. Es ist hilfreich, jedem Faktor einen Namen zu geben, der Ihnen eine Kurzform gibt, um über sie zu sprechen, was Ihre Ergebnisse leichter zugänglich macht. Ziel ist es, Ihre komplexen Daten in ein paar verständliche Themen zu vereinfachen.

Im Folgenden finden Sie einige Richtlinien für die Benennung Ihrer Faktoren:

• Seien Sie beschreibend: Versuchen Sie, das allgemeine Theme zu erfassen, das die Variablen in der Gruppe zusammenfasst.
• Halten Sie es einfach: Ihre Faktornamen sollten leicht zu verstehen und zu kommunizieren sein. Vermeiden Sie technische Jargon oder zu komplexe Phrasen.
• Betrachten Sie Ihre Zielgruppe: Faktornamen sollten für Personen, die Ihre Analyse verwenden, sinnvoll sein. Zum Beispiel wäre „Sauberkeit“ sowohl für Hotelmanager als auch für Hotelgäste sinnvoll.
• Konsistenz: Wenn sich Ihre Umfrage oder Ihr Datenset über verschiedene Domänen oder Feedbacknehmer erstreckt, stellen Sie sicher, dass Ihre Faktornamen konsistent sind.

ASSOCIATED MEASURES & METRICS

Die Faktorentlastungstabelle ist einer der wichtigsten Ausgaben der EFA. Die Faktorbelastung für ein bestimmtes Variable-Faktor-Paar ist die Korrelation zwischen dieser Variable und dem Faktor. Wenn eine Variable für einen bestimmten Faktor eine hohe Faktorlast hat, bedeutet dies, dass die Frage stark mit diesem Faktor verbunden ist.

Die Eindeutigkeit ist der Teil der Varianz, der für die spezifische Variable eindeutig ist und nicht mit anderen Variablen geteilt wird. Eindeutigkeitswerte liegen zwischen 0 und 1, wobei höhere Werte angeben, dass die Variable eindeutig ist und nicht gut in einen der Faktoren passt.

Im Allgemeinen wird empfohlen, Variablen zu entfernen, wenn ihre Faktorbelastungen über 0,3 liegen oder ihre Eindeutigkeit über 0,7 liegt.

IHRE ERGEBNISSE VERWENDEN

Die Faktoranalyse ist ein iterativer Prozess. Daher müssen Sie sie möglicherweise mehrmals mit einer unterschiedlichen Anzahl von Faktoren ausführen, um eine für Sie geeignete Gruppierung zu finden. Für die meisten Forscher ist es wichtig, Gruppierungen von Faktoren zu finden, die neue Einblicke in ihre Daten liefern können, aber Sie können diese Faktoren als neue Variablen in nachfolgenden Analysen verwenden – wie Regression oder Cluster-Analyse.  Sie können beispielsweise eine neue Variable für jeden Faktor anlegen, der den Durchschnittswert aller Variablen verwendet, die darin gruppiert sind.

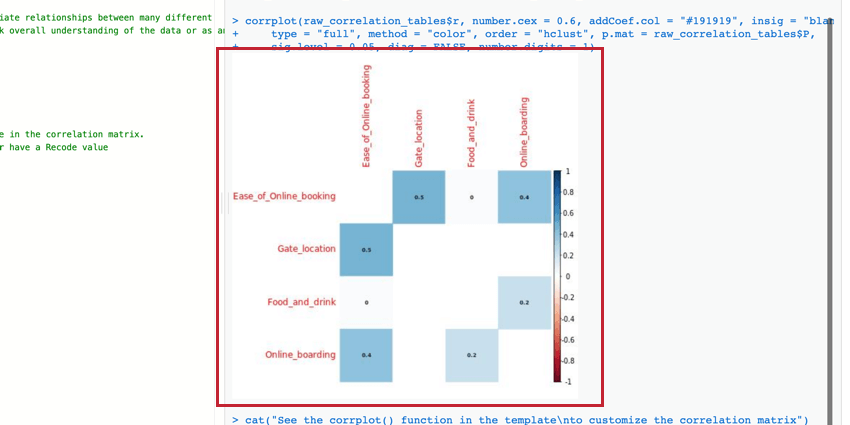
Korrelationsmatrix

Die Korrelationsmatrix ist eine Tabelle, die die Korrelation zwischen den einzelnen bereitgestellten Variablenpaaren anzeigt. Diese Tabelle verwendet Pearsons r standardmäßig, um die Korrelation zu messen, aber Sie können sie in Spearmans Rho ändern, wenn Sie möchten.

Sie können die Parameter der corrplot-Funktion () bearbeiten, um die Tabelle zu ändern und lesbarer zu machen. Weitere Informationen finden Sie im offiziellen R Walkthrough und in der Dokumentation.