Korrespondenzanalyse (BX)
Korrespondenzanalyse
Die Korrespondenzanalyse zeigt die relativen Beziehungen zwischen und innerhalb von zwei Gruppen von Variablen auf, basierend auf den in einer Ausnahmetabelle angegebenen Daten. Für Instanz sind diese beiden Gruppen:
- Instanzen
- Attribute, die übernehmen
Angenommen, ein Unternehmen möchte erfahren, welche Attribute Verbraucher mit verschiedenen Getränkemarken verknüpfen. Die Korrespondenzanalyse hilft dabei, Ähnlichkeiten zwischen Marken und die Stärke von Marken in Bezug auf ihre Beziehungen mit verschiedenen Attributen zu messen. Das Verständnis der relativen Beziehungen ermöglicht es Instanz Ownern, die Auswirkungen vorheriger Aktionen auf verschiedene Instanz Attribute zu ermitteln und über weiter Schritte zu entscheiden.
Die Korrespondenzanalyse ist aus mehreren Gründen wertvoll in der Instanz. Beim Versuch, relativ Beziehungen zwischen Marken und Attributen, Instanz können einen irreführenden Effekt haben; die Korrespondenzanalyse beseitigt diesen Effekt. Die Korrespondenzanalyse bietet auch eine intuitive Schnellansicht der Instanz (basierend auf der Nähe und Entfernung vom Ursprung), die von vielen anderen Diagrammen nicht bereitgestellt wird.
Auf dieser Seite sehen wir uns ein Beispiel für die übernehmen der Korrespondenzanalyse auf einen Anwendungsfall für verschiedene (fiktive) Marken von Sodaprodukten an.
Beginnen wir mit dem Eingabedatenformat – einer Ausnahmetabelle.
Ausnahmetabellen
Eine Ausnahmetabelle ist eine zweidimensionale Tabelle mit Gruppen von Variablen in den Zeilen und Spalten. Wenn unsere Gruppen, wie oben beschrieben, Marken und ihre zugehörigen Attribute wären, würden wir Umfragen durchführen und unterschiedliche Antwortzahlen erhalten, die verschiedene Marken mit den angegebenen Attributen verknüpfen. Jede Zelle in der Tabelle stellt die Anzahl der Antworten oder Zahlen dar, die dieses Attribut mit dieser Instanz verknüpfen. Diese “Assoziation” wird durch eine Umfrage wie “Marken aus einer Liste auswählen, unter der Sie glauben, das Attribut ___ anzuzeigen” angezeigt.
Hier sind die beiden Gruppen “Marken” (Zeilen) und “Attribute” (Spalten). Die Zelle in der unteren rechten Ecke stellt die Anzahl der Antworten für die Instanz “Brawndo” und das Attribut “Wirtschaftlich” dar.
| Geschmackvoll | Ästhetisch | Wirtschaftlich | |
| Butterbier | 5 | 7 | 2 |
| Squishee | 18 | 46 | 20 |
| Slurm | 19 | 29 | 39 |
| Fizzy Lifting Drink | 12 | 40 | 49 |
| Brawndo | 3 | 7 | 16 |
Residuen (R)
In der Korrespondenzanalyse möchten wir die Reste jeder Zelle betrachten. Ein Residuum quantifiziert die Differenz zwischen den beobachteten Daten und den erwarteten Daten – vorausgesetzt, es gibt keine Beziehung zwischen den Zeilen- und Spaltenkategorien (hier wären dies Instanz und Attribut). Ein positiver Rest zeigt uns, dass die Anzahl für diese Instanz viel höher ist als erwartet, was auf eine starke Beziehung hindeutet; entsprechend zeigt ein negativer Rest einen niedrigeren Wert als erwartet, was auf eine schwächere Beziehung hindeutet. Sehen wir uns die Berechnung dieser Reste an.
Ein Rest (R) ist gleich: R = P – E, wobei P die beobachteten Anteile und E die erwarteten Anteile für jede Zelle ist. Lassen Sie uns diese beobachteten und erwarteten Proportionen aufschlüsseln!
Beobachtete Anteile (P)
Ein beobachteter Anteil (P) ist gleich dem Wert in einer Zelle geteilt durch die Gesamtsumme aller Werte in der Tabelle. Für unsere Ausnahmetabelle oben wäre die Gesamtsumme also: 5 + 7 + 2 + 18 … + 16 = 312. Division jedes Zellenwerts durch die Ergebnisse in der folgenden Tabelle für beobachtete Anteile (P).
Beispiel: In der Zelle unten rechts haben wir den Anfangszellenwert 16/312 = 0,051 genommen. Dies zeigt uns den Anteil unseres gesamten Charts, den die Paarung von Brawndo und Economic auf der Grundlage unserer gesammelten Daten darstellen.
| Geschmackvoll | Ästhetisch | Wirtschaftlich | |
| Butterbier | 0.016 | 0.022 | 0.006 |
| Squishee | 0.058 | 0.147 | 0.064 |
| Slurm | 0.061 | 0.093 | 0.125 |
| Fizzy Lifting Drink | 0.038 | 0.128 | 0.157 |
| Brawndo | 0.01 | 0.022 | 0.051 |
Zeilen- und Spaltenmassen
Etwas, das wir aus unseren beobachteten Proportionen leicht berechnen können und später viel verwendet werden, sind die Summen der Zeilen und Spalten unserer Proportionstabelle, die als Zeilen- und Spaltenmassen bezeichnet werden. Eine Zeilen- oder Spaltenmasse ist der Anteil der Werte für diese Zeile/Spalte. Die Reihenmasse für “Butterbeer”, die unsere Karte oben betrachtet, wäre 0,016 + 0,022 + 0,006, was uns 0,044 ergibt.
Ähnliche Berechnungen führen wir am Ende zu Folgendem:
| Geschmackvoll | Ästhetisch | Wirtschaftlich | Zeilenmassen | |
| Butterbier | 0,016 | 0.022 | 0,006 | 0.044 |
| Squishee | 0,058 | 0,147 | 0.064 | 0.269 |
| Slurm | 0.061 | 0.093 | 0,125 | 0.279 |
| Fizzy Lifting Drink | 0,038 | 0,128 | 0,157 | 0.324 |
| Brawndo | 0,01 | 0.022 | 0.051 | 0.083 |
| Spaltenmassen | 0.182 | 0.413 | 0.404 |
Erwartete Anteile (E)
Erwartete Proportionen (E) wären das, was wir in den Proportionen jeder Zelle erwarten, unter der Annahme, dass es keine Beziehung zwischen Zeilen und Spalten gibt. Der erwartete Wert für eine Zelle wäre die Zeilenmasse dieser Zelle multipliziert mit der Spaltenmasse dieser Zelle.
Siehe oben links die Zeilenmasse für Butterbeer multipliziert mit der Spaltenmasse für Tasty, 0,044 * 0,182 = 0,008.
| Geschmackvoll | Ästhetisch | Wirtschaftlich | |
| Butterbier | 0.008 | 0.019 | 0.018 |
| Squishee | 0.049 | 0.111 | 0.109 |
| Slurm | 0.051 | 0.115 | 0.113 |
| Fizzy Lifting Drink | 0.059 | 0.134 | 0.131 |
| Brawndo | 0.015 | 0.034 | 0,034 |
Wir können nun unsere Tabelle mit den Resten (R) berechnen, wobei R = P – E ist. Residuen quantifizieren die Differenz zwischen unseren beobachteten Datenanteilen und unseren erwarteten Datenanteilen, wenn wir davon ausgehen, dass es keine Beziehung zwischen den Zeilen und Spalten gibt.
Wenn wir den negativsten Wert von -0,045 für Squishee und Economic nehmen, würden wir hier interpretieren, dass es eine negative Assoziation zwischen Squishee und Economic gibt; Squishee wird viel seltener als “wirtschaftlich” betrachtet als unsere anderen Getränkemarken.
| Geschmackvoll | Ästhetisch | Wirtschaftlich | |
| Butterbier | 0,008 | 0.004 | -0.012 |
| Squishee | 0.009 | 0.036 | -0.045 |
| Slurm | 0,01 | -0.022 | 0.012 |
| Fizzy Lifting Drink | -0.021 | -0,006 | 0.026 |
| Brawndo | -0,006 | -0.012 | 0.018 |
Indizierte Residuen (I)
Es gibt jedoch einige Probleme mit dem bloßen Lesen von Resten.
Betrachtet man die oberste Zeile aus der obigen Tabelle für die Berechnung von Restwerten, sehen wir, dass alle diese Zahlen sehr nahe an null liegen. Wir sollten nicht die offensichtliche Schlussfolgerung daraus ziehen, dass Butterbeer nicht mit unseren Attributen in Verbindung steht, da diese Annahme falsch ist. Die eigentliche Erklärung wäre, dass die beobachteten Proportionen (P) und die erwarteten Proportionen (E) klein sind, weil, wie unsere Reihenmasse sagt, nur 4,4 % der Stichprobe Butterbeer sind.
Dies wirft ein großes Problem bei der Betrachtung von Resten auf, da wir die tatsächliche Anzahl der Datensätze in den Zeilen und Spalten ignorieren, unsere Ergebnisse zu den Zeilen/Spalten mit größeren Massen verfälscht sind. Wir können dies beheben, indem wir unsere Rückstände durch unsere erwarteten Anteile (E) dividieren und uns eine Tabelle unserer indizierte Reste (I, I = R / E):
| Geschmackvoll | Ästhetisch | Wirtschaftlich | |
| Butterbier | 0.95 | 0.21 | -0.65 |
| Squishee | 0.17 | 0.32 | -0.41 |
| Slurm | 0,2 | -0.19 | 0.11 |
| Fizzy Lifting Drink | -0.35 | -0.04 | 0,2 |
| Brawndo | -0.37 | -0,35 | 0.52 |
Indizierte Reste sind leicht zu interpretieren: Je höher der Wert aus der Tabelle, desto größer ist der beobachtete Anteil im Verhältnis zum erwarteten Anteil.
Wenn man beispielsweise den Wert oben links annimmt, wird Butterbeer 95 % häufiger als „schmackhaft“ angesehen als das, was wir erwarten würden, wenn es keine Beziehung zwischen diesen Marken und Attributen gäbe. Obgleich Butterbeer oben rechts liegt, wird Butterbeer 65 % weniger als „wirtschaftlich“ betrachtet, als wir es erwarten würden – ohne Beziehung zwischen unseren Marken und Attributen.
| Geschmackvoll | Ästhetisch | Wirtschaftlich | |
| Butterbier | 0,95 | 0,21 | -0,65 |
| Squishee | 0,17 | 0,32 | -0,41 |
| Slurm | 0,2 | -0,19 | 0,11 |
| Fizzy Lifting Drink | -0,35 | -0,04 | 0,2 |
| Brawndo | -0,37 | -0,35 | 0,52 |
Angesichts unserer indizierten Rückstände (I), unserer erwarteten Anteile (E), unserer beobachteten Proportionen (P) und unserer Zeilen- und Säulenmassen, lassen Sie uns unsere Korrespondenzanalysewerte für unser Diagramm berechnen!
Koordinaten für die Korrespondenzanalyse berechnen
Einzelwertdekomposition (SVD)
Unser erster Schritt besteht darin, die Singuläre Wertzerlegung (SVD) zu berechnen. Die SVD liefert uns Werte, um die Abweichung zu berechnen und unsere Zeilen und Spalten (Marken und Attribute) darzustellen.
Wir berechnen die SVD auf der standardisierter Rest (Z), wobei Z = I * sqrt(E), wobei I unser indexierter Rest und E unser erwarteter Anteil ist. Die Multiplikation mit E führt dazu, dass unser SVD gewichtet wird, sodass Zellen mit einem höheren erwarteten Wert eine höhere Gewichtung erhalten und umgekehrt, was bedeutet, dass, da erwartete Werte häufig mit der Stichprobe zusammenhängen, “kleinere” Zellen in der Tabelle, bei denen der Stichprobenahme größer gewesen wäre, heruntergewichtet werden. Daher ist die Korrespondenzanalyse mit einer Ausnahmetabelle relativ robust für Ausreißer, die durch Stichprobenahme verursacht werden.
Zurück zu unserem SVD haben wir: SVD = svd(Z). Eine Einzelwertdekomposition generiert 3 Ausgaben:
Ein Vektor d, der die Einzelwerte.
| 1. Dimension | 2. Dimension | 3. Dimension |
| 2.65E-01 | 1.14E-01 | 4.21E-17 |
Eine Matrix, u, die die linke Singularvektoren (Marken).
| 1. Dimension | 2. Dimension | 3. Dimension | |
| Butterbier | -0.439 | -0.424 | -0.084 |
| Squishee | -0.652 | 0.355 | -0.626 |
| Slurm | 0.16 | -0.0672 | -0.424 |
| Fizzy Lifting Drink | 0.371 | 0.488 | -0.274 |
| Brawndo | 0.469 | -0.06 | -0.588 |
Eine Matrix, v, die die rechte Singularvektoren (Attribute).
| 1. Dimension | 2. Dimension | 3. Dimension | |
| Geschmackvoll | -0,41 | -0.81 | -0.427 |
| Ästhetisch | -0.489 | >0.59 | -0.643 |
| Wirtschaftlich | 0.77 | -0.055 | -0.635 |
Die linken Singularvektoren entsprechen den Kategorien in den Zeilen der Tabelle, die rechten Singularvektoren den Spalten. Jeder der einzelnen Werte, zur Berechnung der Varianz, und die entsprechenden Vektoren (d.h. Spalten von u und v), für Zeichnungsstellen, entsprechen einem Dimension. Die Koordinaten, die zur Darstellung von Zeilen- und Säulentypen für unser Korrespondenzanalysediagramm verwendet werden, werden aus den ersten beiden Dimensionen abgeleitet.
Abweichung, ausgedrückt durch unsere Dimensionen
Quadratische Singular-Werte sind bekannt als Eigenwerte (d^2). Die Eigenwerte in unserem Beispiel sind 0,0704, 0,0129 und 0,0000. Die Angabe jedes Eigenwerts als Anteil an der Gesamtsumme gibt an, wie hoch Abweichung erfasst in jeder Dimension unserer Korrespondenzanalyse, basierend auf dem Einzelwert jeder Dimension. Wir erhalten 84,5 % der Abweichung, ausgedrückt durch unsere erste Dimension, und 15,5 % in unserer zweiten Dimension (unsere dritte Dimension erklärt 0 % der Abweichung).
Standardkorrespondenzanalyse
Wir sind nun mit den ressourcen ausgestattet, um die grundlegende Form der Korrespondenzanalyse zu berechnen, unter Verwendung der so genannten Standardkoordinaten, berechnet aus unseren linken und rechten Singularvektoren. Bisher haben wir die indizierten Residuen gewichtet, bevor wir die SVD durchgeführt haben. Um Koordinaten zu erhalten, die unsere indizierten Reste repräsentieren, müssen wir nun die Ausgänge der SVD entgewichten, indem wir jede Zeile der linken Singularvektoren durch die Quadratwurzel der Zeilenmassen dividieren und jede Spalte der rechten Singularvektoren durch die Quadratwurzel der Spaltenmassen dividieren, um die Standardkoordinaten der Zeilen und Spalten für das Plotting zu erhalten.
Instanz:
| 1. Dimension | 2. Dimension | 3. Dimension | |
| Butterbier | -2.07 | -2 | -0,4 |
| Squishee | -1.27 | 0.68 | -1.21 |
| Slurm | 0,3 | -1.27 | -0,8 |
| Fizzy Lifting Drink | 0,65 | 0.86 | -0.48 |
| Brawndo | 1.62 | -0,21 | -2.04 |
Attribut:
| 1. Dimension | 2. Dimension | 3. Dimension | |
| Geschmackvoll | -0.96 | -1.89 | -1 |
| Ästhetisch | -0.76 | 0.92 | >-1 |
| Wirtschaftlich | 1.21 | -0.09 | -1 |
Wir verwenden die beiden Dimensionen mit der höchsten Abweichung, die für das Plotten erfasst wurden, die erste Dimension auf der X-Achse und die zweite Dimension auf der Y-Achse, um unser Standardkorrespondenzanalysediagramm zu generieren.

Wir haben die Grundlage für die Berechnungen festgelegt, die wir für die Standardkorrespondenzanalyse benötigen. Im weiter Abschnitt werden wir die Vor- und Nachteile verschiedener Arten der Korrespondenzanalyse untersuchen, die am besten zu unseren Zwecken passt, um die Analyse von Instanz zu unterstützen.
Arten der Korrespondenzanalyse
Analyse der Zeilen-/Spaltenkapitalkorrespondenz
Die Standardkorrespondenzanalyse ist einfach zu berechnen, und daraus lassen sich starke Ergebnisse ziehen. Die Standardkorrespondenz ist jedoch eine schlechte Antwortmöglichkeit für unsere Anforderungen. Die Abstände zwischen Zeilen- und Spaltenkoordinaten sind übertrieben, und es gibt keine einfache Interpretation der Beziehungen zwischen Zeilen- und Spaltenkategorien. Was wir für die Interpretation von Beziehungen zwischen Zeilen- (Instanz) Koordinaten und Interpretationsbeziehungen zwischen Zeilen- und Spaltenkategorien wünschen, ist Zeilen-Prinzipalnormalisierung (oder, wenn unsere Marken auf unseren Säulen standen, Spaltenprinzipalnormalisierung).
Für die Zeilen-Prinzipalnormalisierung möchten Sie die oben berechneten Standardkoordinaten für Ihre Spaltenwerte (Attribut) verwenden, aber Sie möchten die Hauptkoordinaten für Ihre Zeile (Instanz) berechnen. Die Berechnung der Hauptkoordinaten ist so einfach wie die Verwendung der Standardkoordinaten und deren Multiplikation mit den entsprechenden singulären Werten (d). Für unsere Zeilen möchten wir also einfach unsere Standardzeilenkoordinaten mit unseren einzelnen Werten (d) multiplizieren, die in der folgenden Tabelle dargestellt sind. Für die Spaltenprinzipalnormalisierung würden wir einfach unsere Spalten anstelle unserer Zeilen mit unseren einzelnen Werten (d) multiplizieren.
| 1. Dimension | 2. Dimension | 3. Dimension | |
| Butterbier | -0.55 | -0.23 | 0 |
| Squishee | -0.33 | 0.08 | 0 |
| Slurm | 0,08 | -0.14 | 0 |
| Fizzy Lifting Drink | 0,17 | 0,1 | 0 |
| Brawndo | 0.43 | -0.02 | 0 |
Durch die Ersetzung unserer wichtigsten Koordinaten für unsere Reihen (Marken) erhalten wir am Ende:

Da wir nach unseren einzelnen Werten skaliert haben, stellen unsere Hauptkoordinaten für unsere Zeilen den Abstand zwischen den Zeilenprofilen unserer ursprünglichen Tabelle dar. Sie können die Beziehungen zwischen unseren Zeilenkoordinaten in unserem Korrespondenzanalysediagramm anhand ihrer Nähe zueinander interpretieren.
Der Abstand zwischen unseren Spaltenkoordinaten, da sie auf Standardkoordinaten basieren, ist immer noch übertrieben. Außerdem hat uns die Skalierung nach unseren einzelnen Werten in nur einer der beiden Kategorien (Zeilen/Spalten) eine Möglichkeit gegeben, Beziehungen zwischen Zeilen- und Spaltenkategorien zu interpretieren. Bei einem Zeilenwert und einem Spaltenwert, z.B. Butterbeer (Zeile) und Tasty (Spalte), gilt: Je länger ihre Entfernung zum Ursprung, desto stärker ist ihre Assoziation mit anderen Punkten auf der Karte. Je kleiner der Winkel zwischen den beiden Punkten (Butterbeer und Tasty) ist, desto höher ist die Korrelation zwischen den beiden Punkten.

Der Abstand zum Ursprung in Verbindung mit dem Winkel zwischen den beiden Punkten entspricht der Entnahme des Punktprodukts; das Punktprodukt zwischen einem Zeilen- und Spaltenwert misst die Stärke der Assoziation zwischen den beiden. Wenn die erste und zweite Dimension die gesamte Abweichung in den Daten erklären (zusammen 100 %), entspricht das Punktprodukt direkt dem indexierten Rest der beiden Kategorien. Hier wäre das Punktprodukt der Abstand zum Ursprung der beiden Punkte multipliziert mit dem Kosinus des Winkels zwischen ihnen; .59*2.12*cos(41) = .94. Unter Benutzerkonto von Rundungsfehlern entspricht dies unserem indizierten Restwert von 0,95. Somit stellen Winkel kleiner 90 Grad einen positiv indizierten Rest und damit eine positive Zuordnung dar, und Winkel größer als 90 Grad stellen eine negativ indizierte Rest- oder Negativzuordnung dar.
Skalierte Zeilenkapitalkorrespondenzanalyse
Betrachtet man unser Diagramm oben für die Reihenprinzipalnormalisierung, haben wir eine einfache Beobachtung – die Punkte für unsere Säulen (Merkmale) sind viel breiter verteilt, und unsere Punkte für unsere Zeilen (Marken) sind um den Ursprung geclustert. Dies kann die Analyse unseres Diagramms nach Auge ziemlich schwierig und unintuitiv machen und manchmal unmöglich sein, die Zeilenkategorien zu lesen, wenn sie sich alle überschneiden. Zum Glück gibt es eine einfache Möglichkeit, unser Diagramm zu skalieren, um unsere Spalten einzubringen, während die Fähigkeit, das Punktprodukt (Entfernung vom Ursprung und Winkel zwischen Punkten) zu verwenden, um die Beziehungen zwischen unseren Zeilen- und Spaltenpunkten zu analysieren, bekannt als Skalierte Zeilennormalisierung.
Die skalierte Zeilen-Prinzipalnormalisierung nimmt die Zeilen-Prinzipalnormalisierung an und skaliert die Spaltenkoordinaten auf die gleiche Weise wie die X-Achse der Zeilenkoordinaten – d.h. unsere Spaltenkoordinaten werden um den ersten Wert unserer einzelnen Werte (d) skaliert. Unsere Zeilenwerte bleiben mit der Zeilen-Prinzipalnormalisierung identisch, aber nun werden unsere Spaltenkoordinaten um einen konstanten Faktor herunterskaliert.
| 1. Dimension | 2. Dimension | 3. Dimension | |
| Geschmackvoll | -0.2544 | -0.501 | -0.265 |
| Ästhetisch | -0.201 | 0.2438 | -0,265 |
| Wirtschaftlich | 0.321 | -0,02 | -0,265 |
Das bedeutet für uns, dass unsere Spaltenkoordinaten so skaliert werden, dass sie viel besser zu unseren Zeilenkoordinaten passen, was die Analyse von Trends erheblich erleichtert. Da wir alle unsere Spaltenkoordinaten um denselben konstanten Faktor skaliert haben, haben wir die Streuung unserer Spaltenkoordinaten auf der Karte kontrahiert, aber keine Änderung an ihren Relativitäten vorgenommen. Wir verwenden weiterhin das Punktprodukt, um die Stärke von Assoziationen zu messen. Die einzige Änderung besteht darin, dass, wenn unsere erste und zweite Dimension alle Abweichungen in den Daten abdecken, anstatt dass der indizierte Rest dem Punktprodukt der beiden Kategorien entspricht, sie nun gleich dem skaliert Punktprodukt der beiden Kategorien, d.h. das Punktprodukt, skaliert durch einen konstanten Wert unseres ersten singulären Werts (d). Die Interpretation des Diagramms bleibt mit der Zeilen-Prinzipalnormalisierung identisch.

Kapitalkorrespondenzanalyse
Eine letzte Form der Korrespondenzanalyse, die wir erwähnen werden, ist die Hauptkorrespondenzanalyse, die auch als symmetrische Karte, französische Skalierung oder kanonische Korrespondenzanalyse bezeichnet wird. Anstatt nur die Standardzeilen oder -spalten mit den einzelnen Werten (d) wie in der Zeile/Spalten-Hauptkorrespondenzanalyse zu multiplizieren, multiplizieren wir beide mit den einzelnen Werten. Unsere Standardspaltenwerte, multipliziert mit den einzelnen Werten, ergeben sich also wie folgt:
| 1. Dimension | 2. Dimension | 3. Dimension | |
| Geschmackvoll | -0.2544 | -0.215 | 0 |
| Ästhetisch | -0,201 | 0.105 | 0 |
| Wirtschaftlich | 0,321 | -0,01 | 0 |
Zusammen mit den in der Zeilenprinzipalanalyse berechneten Zeilenwerten erhalten wir Folgendes:

Die kanonische Korrespondenzanalyse skaliert die Zeilen- und Spaltenkoordinaten um die einzelnen Werte. Das bedeutet, dass wir unsere Beziehungen zwischen unseren Zeilenkoordinaten genau so interpretieren können, wie wir es in der Reihen-Prinzipalkorrespondenzanalyse (basierend auf der Nähe) getan haben, UND wir können unsere Beziehungen zwischen unseren Spaltenkoordinaten ähnlich wie bei der Spaltenprinzipalkorrespondenzanalyse interpretieren; wir können Beziehungen zwischen Marken und Beziehungen zwischen Attributen analysieren. Außerdem geht das Zeilen-/Spalten-Clustering in der Mitte der Karte aus der Zeilen-/Spaltenprinzipalanalyse verloren. Was wir jedoch aus der kanonischen Korrespondenzanalyse verlieren, ist eine Möglichkeit, Beziehungen zwischen unseren Marken und Attributen zu interpretieren, etwas sehr nützliches in Instanz.
Vergleich
Standardkorrespondenzanalyse
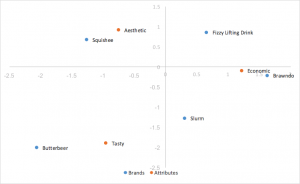
Der einfachste Stil der Korrespondenzanalyse zu berechnen, unter Verwendung linker und rechter Singularvektoren von SVD geteilt durch Zeilen- und Spaltenmassen. Die Abstände zwischen Zeilen- und Spaltenkoordinaten sind übertrieben, und es gibt keine einfache Interpretation der Beziehungen zwischen Zeilen- und Spaltenkategorien.
Korrespondenzanalyse für Zeilennormalisierung
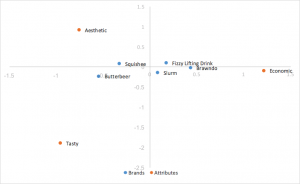
Verwendet Standardkoordinaten von oben, multipliziert jedoch die Zeilenkoordinaten mit den einzelnen Werten, um sie zu normalisieren. Beziehungen zwischen Zeilen (Marken) basieren auf der Entfernung zueinander. Die Abstände der Spalte (Attribut) sind noch übertrieben. Beziehungen zwischen Zeilen und Spalten können vom Produkt dot interpretiert werden. Zeilen (Marken) neigen dazu, in der Mitte verklumpt zu werden.
Skalierte Zeilenprinzipalnormalisierung – Korrespondenzanalyse
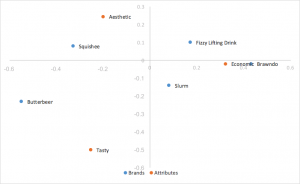
Nimmt die Zeilen-Prinzipalnormalisierung und skaliert die Spaltenkoordinaten um eine Konstante des ersten einzelnen Werts. Dieselben Interpretationen werden als Zeilen-Prinzipalnormalisierung gezeichnet und ersetzen das Punktprodukt durch das skalierte Punktprodukt. Hilft beim Entfernen des Klumps von Zeilen in der Mitte. Dies ist der Stil der Korrespondenzanalyse, den wir bevorzugen.
Principal-Normalisierungskorrespondenzanalyse (symmetrisch, französische Karte, kanonisch)
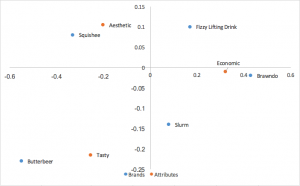
Eine weitere gängige Form der Korrespondenzanalyse, die prinzipiell normalisierte Koordinaten sowohl in den Zeilen als auch in den Spalten verwendet. Beziehungen zwischen Zeilen (Marken) können nach Abstand zueinander interpretiert werden; das Gleiche gilt für Spalten (Attribute). Für Beziehungen zwischen Zeilen und Spalten ist keine Interpretation möglich.
Verschalung
Abschließend wird die Korrespondenzanalyse verwendet, um die relativen Beziehungen zwischen und innerhalb von zwei Gruppen zu analysieren; in unserem Fall wären dies Marken und Attribute.
Die Korrespondenzanalyse beseitigt eine Schieflage bei Ergebnisse verschiedener Massen zwischen Gruppen, indem indizierte Reste verwendet werden. Für Instanz für die Korrespondenzanalyse verwenden wir die Normalisierung des Zeilenprinzips (oder des Spaltenprinzips, wenn die Marken auf den Spalten platziert sind), da dies es uns ermöglicht, Beziehungen zwischen verschiedenen Marken nach ihrer Nähe zueinander zu analysieren, und ermöglicht es uns auch, Beziehungen zwischen Marken und Attributen anhand ihrer Entfernung vom Ursprung kombiniert mit dem Winkel zwischen ihnen und dem Ursprung (dem Punktprodukt) zu analysieren, wobei wir die Beziehung zwischen den Attributen mit übertriebener Bedeutung nicht als wichtig darstellen. Wir verwenden die Normalisierung des skalierten Zeilen-/Spaltenprinzips, um die Analyse unseres Diagramms ohne Kosten zu erleichtern. Wir möchten bedenken, dass wir die Abweichung aus den X- und Y-Achsenbezeichnern (erste und zweite Dimension) addieren, um die in der Karte erfasste Gesamtabweichung anzuzeigen. Je niedriger diese Zahl ist, desto unerklärlicher ist die Abweichung in den Daten und desto irreführender ist die Grafik.
Ein letzter Punkt ist, dass die Korrespondenzanalyse nur Relativitäten Da wir den Massenfaktor unserer Daten eliminiert haben, wird uns unser Graph nichts darüber erzählen, welche Marken die “höchsten” Werte in den Attributen haben. Sobald Sie wissen, wie Sie die Diagramme erstellen und analysieren können, ist die Korrespondenzanalyse ein leistungsstarkes Werkzeug, das Instanz außer Acht lässt, um aussagekräftige und leicht zu interpretierende Erkenntnisse über Beziehungen zwischen und innerhalb von Marken und ihren jeweiligen Attributen zu liefern.