Qu’est-ce que le test t ?
Définition
Le test t, également appelé test de Student ou distribution t, est un test statistique populaire servant à mesurer les différences entre les moyennes de deux groupes ou d’un groupe par rapport à une valeur standard. Il est basé sur une loi de probabilité appelée loi de Student. L’exécution de ce test sert à comprendre si les différences sont statistiquement significatives, c’est-à-dire si elles ne sont pas le fruit du hasard.
En utilisant le test T, un analyste va être en mesure de savoir s’il existe des facteurs qui influencent les différences entre les résultats de plusieurs échantillons observés.
Origines
Ce testing et cette loi de probabilité ont été établis par William Gosset en 1908 lorsqu’il travaillait chez Guinness à Dublin dans le but de contrôler la qualité de la production de bière stout dans la brasserie.
Cependant, Gosset n’a pas été autorisé à publier les résultats de ses recherches en son propre nom. Il a donc adopté le pseudonyme « Student » (étudiant). Cette méthode d’analyse statistique s’est donc popularisé sous ce nom.
Exemple d’application du test de Student
Supposons que vous ayez interrogé deux échantillons de 500 clients issus de deux villes différentes au sujet de leur expérience d’achat dans votre magasin. Le groupe A (clients issus de Lyon) vous a donné en moyenne la note de 8/10 pour la qualité de votre service client tandis que le groupe B (Marseille) vous a attribué une note de 5/10.
Vous devez alors répondre à la question suivante : « Le service fourni au client était-il meilleur à Lyon ou le groupe lyonnais contenait beaucoup de clients ayant vécu une expérience positive ? ».
Les test statistique T vous permettent de répondre à cette question. Il vous indique quelle est la probabilité que les différences observées soient dues au hasard. Si cette probabilité est très faible, la différence est dite significative, ou statistiquement significative.
Dans un test t, vous commencez par établir une hypothèse nulle, c’est-à-dire que les deux populations sont identiques et qu’il n’existe pas de différence significative entre elles. Le test de Student prouvera ou infirmera votre hypothèse nulle.
Découvrez comment CustomerXM fonctionne
Demander une démoQuels sont les différents types de tests T ?
Il existe plusieurs types de test T qui répondent chacun à des besoins différents et permettent d’obtenir des résultats statistiques particuliers.
Test t à 1 échantillon
Au lieu de comparer les données de votre échantillon à celles d’un second segment marketing, vous pouvez exécuter ce test (1-sample t-test) pour comparer ces data à une valeur ou un nombre défini. Cela est particulièrement utile pour comparer des tendances ou identifier des fluctuations.
Exemple : les dépenses mensuelles moyennes de mes clients sont-elles nettement supérieures ou inférieures à 50 € ?
Test t à 2 échantillons
Le test à 2 échantillons (2-sample t-test en anglais) s’agit de la technique d’analyse la plus standard et classique. Elle compare les moyennes de deux populations indépendantes pour identifier une différence significative.
Exemple : les acheteurs strasbourgeois se rendent-ils plus fréquemment en magasin que les clients dijonnais ?
Test t apparié
Avec une distribution t appariée (paired t-test), vous testez deux groupes dépendants pour voir s’ils sont significativement différents. Cette étude est particulièrement utile pour visualiser des évolutions et faire des comparatifs « avant / après ».
Exemple : Les dépenses mensuelles moyennes par client ont-elles augmentées de manière significative après le lancement de la campagne marketing Y ?
Les tests t bilatéraux et unilatéraux
Pour chaque type de testing, vous pouvez choisir si vous souhaitez mener un examen unilatéral ou bilatéral.
Le test t unilatéral vous indique seulement si la différence entre les moyennes étudiées est significative ou non. Le test t bilatéral vous indique quelle moyenne est la plus élevée des deux.
Quand est-il judicieux d’utiliser le test de Student ?
Une étude basée sur un ou deux échantillons seulement
Ce type d’analyse peut être utilisé lorsqu’on étudie un ou deux groupes, qu’ils soient dépendants ou indépendants. Pour mener des analyses statistiques avec un nombre d’échantillons supérieur, l’ANOVA est une meilleure solution.
Il existe également d’autres conditions d’utilisation spécifiques aux tests à 2 échantillons.
Une étude avec un échantillon suffisamment grand
Quel que soit le type de distribution T que vous souhaitez exécuter pour réaliser votre analyse statistique, vous devez vous assurer que vos échantillons soient de taille suffisamment grande pour que les données soient fiables et pertinentes. Cependant, l’un des avantages du test de Student est qu’elle vous permet de travailler avec des quantités de données relativement petite. En effet, cette analyse statistique repose sur la moyenne et la variance de l’échantillon et non sur la population dans son ensemble.
Conditions spécifiques pour le test à 2 échantillons
Pour mener une analyse de Student avec deux échantillons de référence, il faut que votre étude regroupe les caractéristiques suivantes :
- Vos données sont exprimées en intervalle ou sur une échelle ordinale (classement ou score numérique par exemple)
- Les deux groupes que vous comparez dont indépendants l’un de l’autre et n’ont pas d’effets l’un sur l’autre (cette condition ne s’applique pas lorsque l’on effectue une distribution t appariée)
- Votre échantillon doit être aléatoire
- La distribution est normale, c’est-à-dire que les résultats forment une courbe en cloche où la moyenne intervient au milieu
- Il y a une quantité similaire de variance dans chaque groupe : la dispersion des points de données est similaire pour les deux populations étudiées
Autres types d’analyses statistiques dérivées du test T
Le tableau ci-dessous vous présente d’autres techniques d’analyses statistiques qui peuvent être utilisées pour examiner ce type de données lorsque différents niveaux de mesure sont disponibles.
| NIVEAU DE MESURE | |||
|---|---|---|---|
| Type d’échantillon |
|
|
|
| 2 échantillons appariés |
|
|
|
| Échantillons indépendants |
|
|
|
Comment mener un test T ?
Les éléments nécessaires au calcul
Pour exécuter une distribution T de Student, vous avez besoin de 5 éléments :
- La différence entre les valeurs moyennes de vos ensembles de données
- L’écart type pour chaque échantillon (la variance)
- Le nombre de données dans chaque groupe
- Une valeur 𝝰 (alpha) : c’est la marge d’erreur acceptable. Une valeur 𝝰 de 0,05 signifie un taux d’erreur acceptable de 5%
- Pour les calculs manuels, vous aurez besoin d’un tableau des valeurs critiques qui vous aidera à interpréter vos résultats. Cliquez sur le lien suivant pour obtenir un tableau de valeurs critiques en ligne.
Une fois que vous avez ces 5 éléments en votre possession, vous pouvez soit utiliser des formules pour exécuter votre test t manuellement (formules disponibles plus bas dans l’article), soit utiliser un progiciel de statistique tel que SPSS ou Minitab pour calculer automatiquement vos résultats.
Les résultats de l’analyse et leur interprétation
En menant une distribution T de Student, vous obtenez plusieurs types de résultats et plusieurs data.
La valeur T
La valeur T est composée de deux éléments : la différence entre les moyennes des deux groupes étudiés et la variance entre eux. Ces deux éléments sont exprimés sous forme de ratio.
Si le ratio est petit, il n’y a pas beaucoup de différence entre les deux. S’il est élevé, la différence entre ces deux groupes est importante.
Le degré de liberté
Ce résultat est directement lié à la taille de l’échantillon et à la mesure dans laquelle les valeurs qu’il contient peuvent varier tout en conservant la même moyenne.
Numériquement, il s’agit de la taille de l’échantillon moins 1. Vous pouvez également le considérer comme le nombre de valeurs dont vous avez besoin pour connaître toutes les valeurs.
La valeur p
SI vous effectuer le calcul via la formule manuellement, vous pouvez utiliser votre tableau de valeurs critiques pour trouver la valeur p.
La valeur p est le résultat qui vous permet de savoir si la différence entre les moyennes est statistiquement significative ou non. C’est l’objectif du test de Student, la valeur qui va vous indiquer si les différences sont le fruit du hasard ou non.
Stats iQ : des résultats facilement compréhensibles par tous
Nous savons que les utilisateurs de logiciels d’enquêtes ne sont pas tous des analystes ou des statisticiens experts. C’est pourquoi nous avons développé Stats iQ. Cet outil de calcul puissant vous permet de réaliser des analyses statistiques en quelques clics et d’obtenir des résultats facilement compréhensibles, interprétables et utilisables.
Vous pouvez ainsi exécuter des tests statistiques comme le test T ou l’ANOVA sans connaissance approfondie en statistique et obtenir des conclusions qui vont pouvoir nourrir vos études de marché et vos stratégies marketing.
Formules pour le calcul manuel du test T de Student
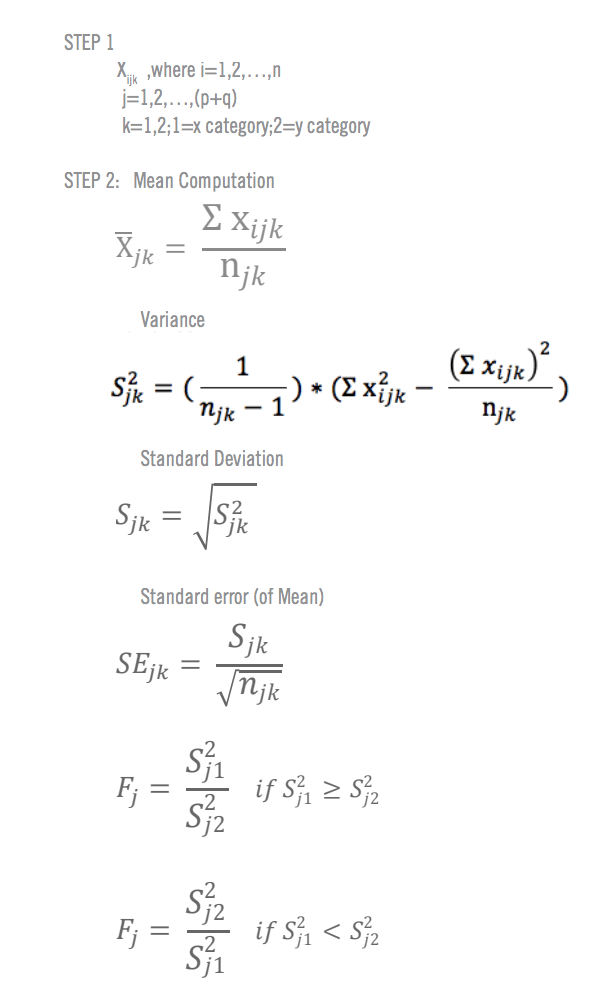
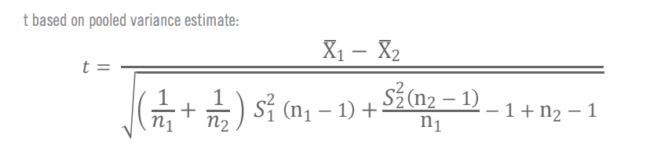

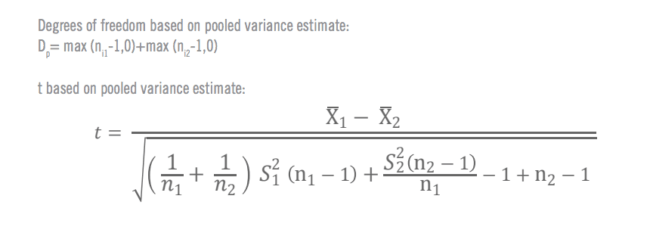

Voyez comment Qualtrics iQ peut accélérer l'analyse de vos enquêtes.