Comment utiliser la tabulation croisée dans les études de marché ?

Qu’est-ce que la tabulation croisée ?

Définition

La tabulation croisée, également appelé tableau de contingence, est un tableau à deux entrées (ou plus) qui répertorie le nombre de répondants possédant des critères spécifiques étudiés lors d’un sondage.

Bien utilisés, les tableaux de contingence fournissent une mine d’informations sur les relations, corrélations, dépendances ou indépendances entre différentes données.

Appellations et vocabulaire spécifique de l’analyse croisée

Dans le domaine marketing, cette méthode analytique peut se nommer de multiples manières :

• Analyse croisée
• Analyse par tableau de contingence
• Test chi deux
• Tabulation des données

Ces analyses possèdent également un langage propre. Banners, stubs, valeurs attendues ou statistiques du chi-deux sont des termes que vous devriez entendre si votre équipe marketing utilise cette technique analytique pour créer des études de marché.

Pour comprendre les experts de la tabulation croisée, voici quelques explications lexicales :

• « Bannières » désigne les variables en colonnes : souvent la liste des caractéristiques et critères étudiés
• « Stubs » désigne les données en ligne : une population ou un segment de consommateurs par exemple
• « Chi-deux», « Khi-deux » ou « chi carré » (écrit χ²) est un test statistique qui permet de tester l’indépendance de deux variables
• « Valeur attendue» signifie la valeur moyenne supposée d’un phénomène aléatoire. Concrètement, dans une expérience de probabilité, la valeur attendue est la moyenne de la somme de toutes les valeurs qu’il est probable d’obtenir.

Exemple d’utilisation du tableau de contingence

Un chercheur souhaite établir et évaluer la corrélation entre la ville de résidence d’un groupe défini de personnes et le fait qu’elles soient fans de telle ou telle équipe sportive. Il va alors rentrer dans sa table deux types de variables : « Ville de résidence » et « Equipe de baseball préférée ».

En rentrant les nombres correspondants (fréquence) et en calculant les pourcentages relatifs, il va ainsi pouvoir voir si la ville de résidence et le fait d’être fan d’une équipe spécifique est indépendante ou lié.

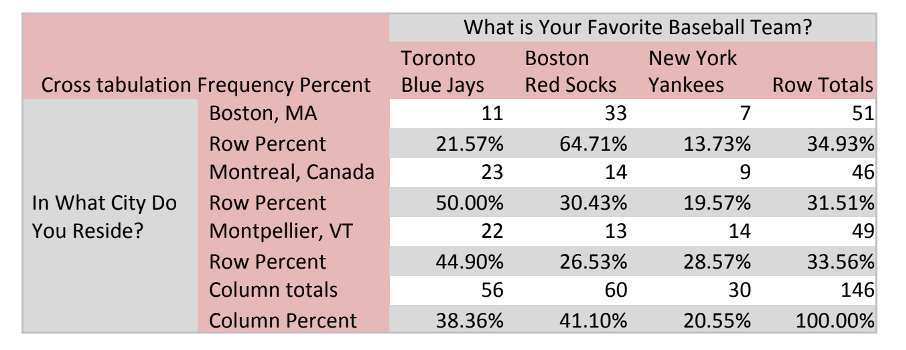
Dans ce tableau, une légende décrit la nature des variables en lignes et en colonnes.

Tableau de contingence avec analyse du chi-deux : principes de base

Le test statistique χ² est la principale méthode probabiliste utilisée dans l’analyse des tableaux croisés. Cette étude statistique détermine si deux paramètres sont dépendants ou indépendants.

Si les variables sont indépendantes (l’une n’ayant pas d’impact direct sur l’autre), alors les résultats du test statistiques seront « non significatifs » et l’hypothèse nulle ne peut être rejetée. En d’autres mots, il n’y a pas de relations entre les variables étudiées.

Au contraire, si l’étude croisée démontrent un lien entre les variables, les résultats du test statistique seront « statistiquement significatifs » et l’hypothèse nulle peut être rejetée. Lorsque les variables sont liées faiblement (par exemple, une probabilité d’interdépendance équivalente à 5%), on dit que les résultats sont statistiquement significatifs au niveau 0,05 ou 5%.

Cette valeur de 5% est régulièrement prise comme taux d’erreur probable. En effet, dans toute analyse, et même en sélectionnant un échantillon ou panel conséquent et suffisamment représentatif d’une population spécifique, il existe une marge d’erreur probable qu’il faut absolument prendre en compte dans ses études analytiques.

Calcul statistique du chi-deux avec les tableaux de contingence

Méthodologie et formule de calcul du chi carré

La statistique du chi carré est calculée en mesurant d’abord une valeur khi-deux pour chaque cellule individuelle du tableau avant de les additionner pour former une valeur totale χ² pour le tableau complet.

Le khi carré est obtenu grâce à la formule suivante :

χ²= (Valeur observée – Valeur attendue) x 2 / Valeur attendue.

Dans l’exemple ci-dessous, les calculs du khi deux sont surlignés en gris.

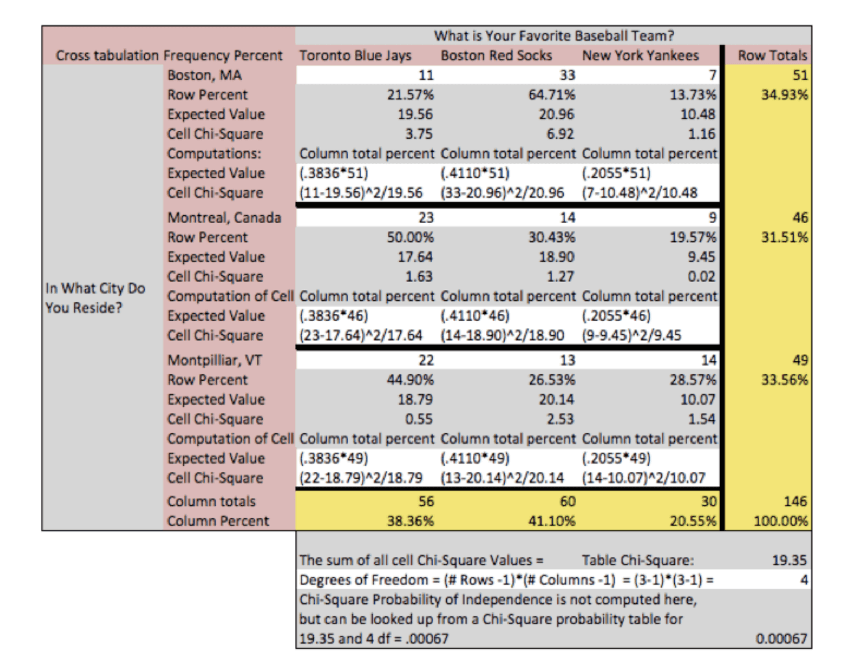
Exemple d’interprétation des résultats des tests statistiques du khi deux

Dans l’exemple ci-dessus, nous observons que la valeur χ² du tableau de contingence total est 19,35. La probabilité associée est de moins d’1 sur 1000. Nous pouvons donc rejeter l’hypothèse nulle et concluons qu’il doit y avoir une relation de dépendance entre les paramètres. Nous pouvons d’ailleurs observer cette relation à deux endroits du tableau.

En effet, en observant les valeurs individuelles du chi carré, cette constatation paraît plus qu’évidente. Nous observons que dans les cellules arrivant au croisement de « Red Socks et Boston », de « Red Socks et Montpillar Vermont » et de « Blue Jays et Montréal », le nombre de répondants surpasse la valeur attendue. Par exemple, une fréquence de 33 répondants au lieu des 20,94 attendus pour la cellule « Red Socks et Boston ».

Au contraire, en comparant les résultats attendus et observés dans les cellules qui arrivent au croisement entre « Yankees et Montréal », « Red Socks et Montpillar Vermont » ou encore « Red Socks et Montréal », on observe que la fréquence est plus faible que prévue.

Analyse du tableau de contingence sans la méthode du chi carré

Étant donné que le chi carré de la cellule et les valeurs attendues ne sont pas souvent affichés dans les tableaux croisés, nous aurions pu arriver à la même conclusion sans le test statistique du chi deux. Ce résultat aurait pu être trouvé en comparant simplement le pourcentage du total de la colonne au pourcentage de réponses positives d’une variable.

Dans la ligne « Boston Red Socks », nous comparerions 41,10% (nombre de fan sur les 3 villes confondues) à 64,71% (nombre de fans résidant uniquement à Boston). Nous pouvons constater que la proportion de fans des Red Socks est plus importante à Boston que la fréquence de fans cumulés dans les 3 villes.

Dans ce tableau croisé, l’écart entre ces deux proportions est le plus important. Cependant, il faut être prudent quant à l’interprétation des résultats obtenus. L’analyse permet de constater des faits et non une causalité.

Par exemple, nous ne pouvons pas affirmer que le fait d’être fan des Red Socks pousse les individus à déménager à Boston. La probabilité d’être fan des Red Socks lorsqu’on réside à Boston est importante mais l’une ou l’autre des variables n’est pas forcément la conséquence directe de l’autre. Ces données sont probablement indépendantes lorsque l’on considère d’autre concepts ou paramètres.

L’utilisation du tableau de contingence dans les études de marché

Le tableau de contingence constitue un outil puissant pour observer des relations entre différents facteurs ou variables. C’est d’ailleurs la raison pour laquelle il est très utilisé dans la conception des études statistiques de marché.

Cette méthode analytique est particulièrement utile lors de la phase de conception d’un projet ou pour effectuer un lancement optimal de nouveaux produits ou services.

Elle peut par exemple permettre d’affiner une offre et une stratégie marketing. Grâce à l’analyse croisée, une entreprise peut préciser la cible de ses produits ou services (lieu de résidence, sexe, âge, etc.) ou perfectionner son offre en intégrant des critères essentiels pour le public visé.