Cómo calcular el tamaño de una muestra: asegúrese de que el muestreo sea correcto

¿Qué es el tamaño de la muestra?

El tamaño de la muestra es un término que se suele usar en estadística y en investigación de mercado. Surge siempre que se desea encuestar a una gran cantidad de personas. Tiene relación con la forma en que se encuesta a grandes segmentos.

Entonces, ¿qué es muestreo y por qué el tamaño de la muestra es importante?

Al encuestar a un gran número de personas, lo que en realidad interesa es comprender al grupo completo. Sin embargo, no es factible obtener respuestas de absolutamente todos. En cambio, lo que se hace es tomar una muestra aleatoria de personas que represente a la población total a investigar (también llamada “universo”). Este proceso se conoce como muestreo.

El tamaño de la muestra es fundamental para obtener resultados representativos y estadísticos, y para que el estudio sea exitoso.

• Si la muestra es demasiado pequeña, podría incluir una cantidad desproporcionada de encuestados atípicos (o “outliers”, en inglés), que generen valores anómalos. Esto puede producir una distorsión de los resultados, lo que no le permitirá obtener una visión realista de la población del estudio.
• Si la muestra es demasiado grande, la investigación se vuelve demasiado compleja, costosa y lenta. Si bien los resultados serán más precisos, sus beneficios no superarán los costos de realizar el estudio.

Si ya ha determinado sus variables, puede obtener el tamaño de la muestra adecuado rápidamente, con la siguiente calculadora de tamaños de muestra en línea:

En los siguientes pasos, podrá ver cómo calcular el tamaño de la muestra adecuado para su investigación de mercado, desde el principio.

Cómo calcular el tamaño de una muestra

Para calcular el tamaño de la muestra adecuado, se deben tener en cuenta diferentes factores que afectan a la encuesta y tener una comprensión básica de los cálculos estadísticos que se aplican. Luego, podrá utilizar una fórmula de tamaño de muestra para aplicar todo esto y hacer el muestreo con la confianza de que su encuesta será estadísticamente correcta.

Los pasos que siguen son adecuados para calcular el tamaño de la muestra para datos continuos, es decir, datos que se contabilizan numéricamente. Esto no se aplica a datos categóricos, es decir, datos que se agrupan en categorías, como verde, azul, hombre, mujer, etc.

Etapa 1: determinar las variables del tamaño de la muestra

Antes de poder calcular el tamaño de la muestra, es necesario determinar ciertos aspectos de la población objetivo y del grado de precisión que se necesita:

1. Tamaño de la población

¿Cuántas personas en total conforman el segmento que desea estudiar? Para saberlo, debe tener claro quién forma parte del grupo de población y quién no. Por ejemplo, si se desea saber más sobre dueños de perros, debe incluir a todas las personas que, en algún momento, hayan tenido al menos un perro (dependiendo de los objetivos de la encuesta, podría incluir o no a aquellos que tuvieron perro anteriormente, pero no en la actualidad). No se preocupe si no puede calcular el número exacto. Es habitual iniciar la investigación de mercado con un tamaño de población desconocido o un rango estimado.

2. Margen de error (intervalo de confianza)

Es inevitable que se produzcan errores. Lo importante es determinar qué grado de error será aceptable en su estudio. El margen de error, también llamado intervalo de confianza, se expresa en valores medios. Es necesario establecer qué diferencia se aceptará entre la media de la muestra y la media de la población a estudiar. Si alguna vez vio una encuesta política, entonces ha visto un intervalo de confianza y cómo se expresa. Se ve como algo parecido a esto: “El 68 % de los votantes aprobaron la propuesta Z, con un margen de error de +/– 5 %”.

3. Nivel de confianza

Esto es lo que sigue al intervalo de confianza del paso 2. Se refiere a cuánta confianza se desea tener en que la media real se encontrará dentro del margen de error. Los intervalos de confianza más comunes son de un 90 %, un 95 % y un 99 % de confianza.

4. Desviación estándar

En este paso, se debe estimar cuánto variarán las respuestas que se reciban entre sí y con respecto a la media. Una desviación estándar baja significa que todos los valores se agruparán en torno a la media, mientras que una desviación estándar alta significa que se distribuirán en un rango mucho más amplio, con valores atípicos muy pequeños y muy grandes. Dado que aún no se ha realizado la encuesta, lo más seguro es optar por una desviación estándar de 0,5, que garantizará que el tamaño de la muestra sea lo suficientemente grande.

Etapa 2: calcular el tamaño de la muestra

Ahora que determinó los valores de los pasos anteriores, podrá calcular el tamaño de la muestra que necesita. Puede hacerlo con una calculadora de tamaños de muestra en línea o con papel y lápiz.

5. Determinar la puntuación Z

Lo siguiente que debe hacer es convertir el nivel de confianza en una puntuación Z. Estas son las puntuaciones Z para los niveles de confianza más comunes:

• 90 % – Puntuación Z = 1,645
• 95 % – Puntuación Z = 1,96
• 99 % – Puntuación Z = 2,576

Si elige otro nivel de confianza, puede usar esta tabla de puntuación Z (un recurso que pertenece a SJSU.edu y que está alojado en sus servidores) para determinar la puntuación.

6. Use la fórmula del tamaño de la muestra

Ingrese la puntuación Z que obtuvo, la desviación estándar y el intervalo de confianza en la calculadora de tamaños de muestra o utilice esta fórmula para calcularlo manualmente:

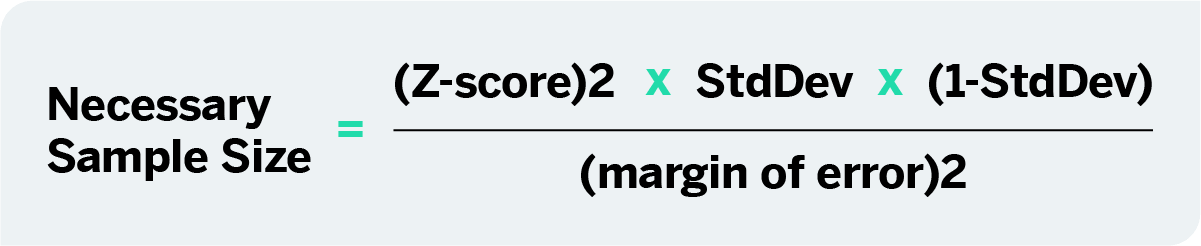
Esta ecuación se utiliza para un tamaño de población desconocido o muy grande. Si el universo a estudiar es conocido y más pequeño, simplemente utilice la calculadora de tamaños de muestra.

¿Qué significa esto en la práctica?

Aquí hay un ejemplo práctico. Supongamos que elige un nivel de confianza del 95 %, una desviación estándar de 0,5 y un margen de error (intervalo de confianza) de +/– 5 %.

((1,96)2 x 0,5(0,5)) / (0,05)2

(3,8416 x 0,25) / 0,0025

0,9604 / 0,0025

384,16

Se necesitan 385 encuestados.

¡Y listo! Acaba de calcular el tamaño de la muestra.

Problemas con el tamaño de la muestra

Si el tamaño de la muestra es demasiado grande, puede ajustar los resultados de alguna de las siguientes formas:

• Disminuir el nivel de confianza.
• Incrementar el margen de error.

Esto aumentará las posibilidades de que el muestreo tenga errores, pero reducirá considerablemente la cantidad de respuestas que necesitará.