Was ist eine Stichprobe?
Stichproben dienen der Repräsentation der Gesamtpopulation oder der Grundgesamtheit. Es handelt sich um eine ausgewählte Teilmenge, die sich hochrechnen und verallgemeinern lässt, um allgemeingültige Aussagen über größere oder schwer fassbare Gruppen – beispielsweise ein Wahlvolk – treffen zu können. Die Gesamtzahl der Stichproben wird als Stichprobengröße bzw. Stichprobenumfang bezeichnet. Je größer diese ausfällt, desto aussagekräftiger wird das Ergebnis. Im gleichen Zug sinkt die Wahrscheinlichkeit auf Stichprobenfehler und somit auch die Irrtumswahrscheinlichkeit.
Sowohl die Reliabilität einer Stichprobe als auch ihr Umfang und ihre Repräsentativität spielen eine bedeutende Rolle für gute und aussagekräftige Ergebnisse.
Ein Beispiel für Stichproben wäre:
- Grundgesamtheit → Erstsemesterstudierende in Berlin
- Stichprobe → Erstsemesterstudierende drei zufällig gewählter Studiengänge
- Statistische Einheit → eine befragte Studentin
- Merkmal → Englischkenntnisse
- Merkmalsausprägung → Englischkenntnisse: 78 %
Testen Sie Qualtrics kostenlos
KONTO ERSTELLENDer Sample Size Calculator von Qualtrics
Um die ideale Stichprobengröße berechnen zu können, müssen Sie zunächst die Felder des Sample Size Calculators von Qualtrics ausfüllen. Dabei erfragt dieser das Konfidenzniveau, die Populationsgröße und die Fehlermarge. Daraus berechnet der Stichprobenrechner die ideale Stichprobengröße für die gewünschte Umfrage:
Was bedeuten die Felder des Sample Size Calculators?
Damit unser Sample Size Calculator ein optimales Ergebnis liefern kann, bedarf es einiger entscheidender Variablen. Eine große Schwierigkeit für Forscher stellt die Anzahl der Antworten für statistisch einwandfreie Ergebnisse dar: Wann ist eine Stichprobe repräsentativ?
Während ein größerer Stichprobenumfang genauere Studienresultate liefern kann, geht dieser in der Regel auch mit einem höheren Preis und Aufwand einher. Es gilt herauszufinden, wann Kosten und Ergebnisse ausgewogen sind und eine Studie als sinnvoll und repräsentativ zu erachten ist.
Konfidenzniveau, Fehlermarge und Populationsgröße sind essenzielle Schlüsselwerte, um eine Stichprobengröße berechnen zu können. Doch worum handelt es sich bei den einzelnen Werten und worauf ist dabei zu achten?
Fehlermarge bzw. Fehlerspanne
Die Fehlermarge gibt voraussichtliche Abweichungen von den Resultaten der Stichprobe zur Gesamtpopulation als Prozentsatz an. Die Marge bezieht sich somit auf die Anzahl der zugelassenen Fehler in den Ergebnissen, denn keine Stichprobe ist perfekt.
Was es zudem über die Fehlermarge zu wissen gilt:
- Wählen Sie im Stichprobenrechner eine kleinere Fehlermarge, erhalten Sie ein genaueres Ergebnis, müssen allerdings mit einem höheren Stichprobenumfang
- Die Fehlermarge wird als positive oder negative Prozentangabe
- Wenn 70 % für Möglichkeit zwei stimmen und die Fehlermarge +/- 10 % beträgt, bedeutet dies, dass die Studienleiter sicher sind, dass zwischen 60 % und 80 % der Gesamtpopulation Möglichkeit zwei wählen würden.
Konfidenzniveau der Stichprobe
Das Konfidenzniveau beim Stichprobenrechner steht in direktem Bezug zur Fehlermarge. Es bestimmt, wie sicher es ist, dass die Gesamtpopulation von der berechneten Stichprobe repräsentiert wird und sich die Ergebnisse dementsprechend in der angegebenen Fehlermarge befinden.
Wichtig zu wissen:
- Das Konfidenzniveau wird ebenfalls in Prozent
- Je höher das Konfidenzniveau, desto präziser die Genauigkeit.
- Ein höheres Konfidenzniveau erfordert eine umfassendere Stichprobengröße.
- Wenn unter Einberechnung der Fehlermarge zwischen 60 % und 80 % der Gesamtpopulation Möglichkeit 2 wählen würden und das Konfidenzniveau mit 90 % angegeben wird, bedeutet dies: Die Sicherheit, dass zwischen 60 % und 80 % tatsächlich diese Wahl treffen, liegt bei 90 %.
- Am häufigsten werden Konfidenzniveaus von 90 %, 95 % oder 99 % gewählt.
Populationsgröße
Die im Stichprobenrechner angegebene Populationsgröße ist die Grundgesamtheit der zu untersuchenden Personen. Dies kann die Bevölkerung eines Landes sein, die Jahrgangsstufe einer Schule oder etwas Ähnliches. Generell lässt sich sagen: Je größer die Stichprobengröße bei gleichbleibender Populationsgröße ausfällt, desto höher ist ihre statistische Signifikanz. Ist die Stichprobengröße zu klein, steigt das Risiko, dass es sich um zufällig entstandene Ergebnisse handelt. Während es bei kleinen Studien ratsam ist, mit einer möglichst präzisen Populationsgröße zu arbeiten, lässt sich für größere Studien auch ein Schätzwert verwenden. Denn je kleiner die Gruppe, desto wichtiger ist Präzision, um eine repräsentative statistische Auswertung zu erhalten.
Die folgenden Hinweise können bei der Bestimmung der geeigneten Populationsgröße hilfreich sein:
- Handelt es sich um die Untersuchung einer lokalen Organisation mit 15 Mitarbeitern, empfiehlt es sich, die Populationsgröße akkurat
- Bei größeren Studien haben Abweichungen eine geringere statistische Auswirkung. Zudem ist es in vielen Fällen nicht möglich, eine präzise Zahl für die Populationsgröße herauszufinden.
- Handelt es sich beispielsweise um die Bevölkerung Deutschlands, würde es reichen, von 83 Millionen Menschen auszugehen, wobei der tatsächlich Wert um einige Hunderttausende abweicht.
Übersicht: Wirkung der Schlüsselwerte auf die Umfrageergebnisse
Die folgende Übersicht veranschaulicht die Auswirkungen der einzelnen Variablen auf die Genauigkeit der Umfrageergebnisse:
| Schlüsselwert | Höherer Wert | Niedrigerer Wert |
|---|---|---|
| Stichprobengröße | Genauigkeit steigt | Genauigkeit sinkt |
| Fehlermarge | Genauigkeit sinkt | Genauigkeit steigt |
| Konfidenzniveau | Genauigkeit steigt | Genauigkeit sinkt |
| Populationsgröße | Genauigkeit sinkt | Genauigkeit steigt |
Weitere Schlüsselwerte einer Stichprobe bestimmen
Um die optimale Stichprobengröße selbst berechnen zu können, sind zudem folgende Aspekte und Variablen über die Gesamtpopulation und die benötigte Stichprobe festzulegen.
Standardabweichung
Die Standardabweichung gibt an, wie viel Varianz bei den Antworten zu erwarten ist. Je höher die Varianz ist, desto größer ist auch die Standardabweichung. Sie zeigt an, wie dicht die Daten sich um den Mittelwert häufen und wie weit sie sich zwischen Maximum und Minimum verteilen. Da dies vor der Durchführung der Studie nicht wirklich feststellbar ist, wird dieser Wert meist auf 0,5 (50 %) gesetzt. Mit diesem Wert, der den Schlimmstfall darstellt, lässt sich sichergehen, dass der ermittelte Stichprobenumfang groß genug ist, um für die Gesamtpopulation repräsentativ zu sein. Zudem bilden extreme Antworten wahrscheinlicher ein akkurates Bild ab als moderate Resultate.
Der Z-Wert
Der auf dem Konfidenzniveau basierende Z-Wert ist konstant und stellt den üblichen Mittelwert dar. Außerdem bezeichnet er die Nummer an Standardabweichungen, die zwischen dem gewählten Wert und dem Populationsdurchschnitt liegen.
Da es relativ komplex ist, den Z-Wert manuell auszurechnen oder ihn anhand einer Z-Wert-Tabelle zu ermitteln, sind im Folgenden die Z-Werte für häufig festgelegte Konfidenzniveaus zu finden:
- 80 % Konfidenzniveau → 1,28 Z-Wert
- 85 % Konfidenzniveau → 1,44 Z-Wert
- 90 % Konfidenzniveau → 1,65 Z-Wert
- 95 % Konfidenzniveau → 1,96 Z-Wert
- 99 % Konfidenzniveau → 2,58 Z-Wert
Formel zur Berechnung der Mindestgröße einer Stichprobe
Stehen die Schlüsselwerte fest, geht es an die Berechnung der Stichprobengröße. Es gilt eine repräsentative Stichprobe zu wählen, die dennoch realistisch durchführbar ist. Verschiedene Formeln helfen unter Berücksichtigung der Schlüsselwerte, einen sinnvollen Stichprobenumfang zu finden.
Standardformel
Die Standardformel gilt vor allem für kleinere oder mittlere Gesamtpopulationen. Anhand dieser lässt sich die Stichprobe unkompliziert berechnen:
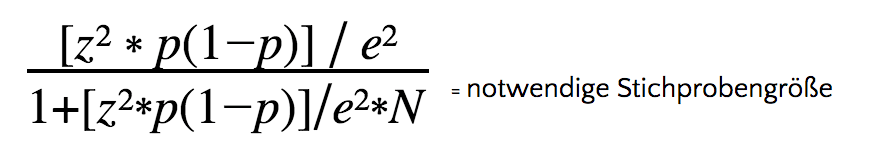
Die Standardformel lässt sich anhand des folgenden Beispiels verdeutlichen:
Gesamtpopulation / Populationsgröße (N) = 500
Z-Wert (z) = 1,96
Fehlermarge (e) = 0,1
Standardabweichung (p) = 0,5
Daraus folgt dieses Rechenbeispiel:
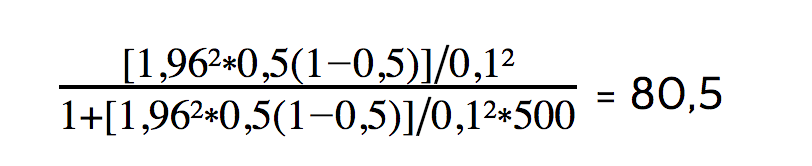
Formel für sehr große oder unbekannte Populationen
Handelt es sich um eine Gesamtpopulation, deren Größe sich nicht genau festlegen lässt oder die sehr umfangreich ist, reicht es, den oberen Teil der Standardformel zu verwenden.
Diese sieht dann wie folgt aus:
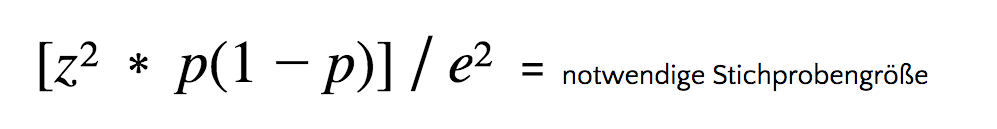
Sind die Schlüsselwerte – mit Ausnahme der Populationsgröße – wie oben angegeben, ergibt sich folgendes Resultat:
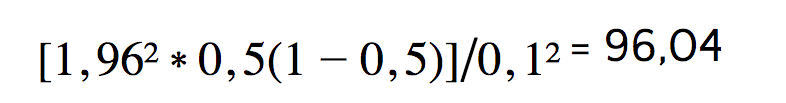
Erscheint die Stichprobengröße zu umfangreich, ist es möglich, das Konfidenzniveau zu reduzieren oder die Fehlermarge zu erhöhen. Dadurch steigt zwar die Anzahl der möglichen Fehler in der Stichprobe, doch die Summe der benötigten Antworten sinkt und dadurch auch die Kosten und der Aufwand der Studie.
Fundierte Umfragen durchführen mit Qualtrics
Neben einem Sample Size Calculator bietet Qualtrics XM Ihnen zahlreiche weitere Tools, um fundierte Umfragen, Marktforschungen oder Statistiken vorzubereiten und durchzuführen. Unter anderem bieten wir Ihnen Zugänge zu Online-Panels, über die Sie die passenden Teilnehmer finden, sowie Vorlagen für Fragebögen und Tools zum Erstellen und Versenden einer Umfrage.
Testen Sie Qualtrics kostenlos