Was ist eine Regressionsanalyse?
Bei der Regressionsanalyse handelt es sich um ein statistisches Analyseverfahren, das die Beziehung zwischen einer abhängigen und einer oder mehreren unabhängigen Variablen modelliert. Damit gehört sie zu den sogenannten multivariaten Analysemethoden. In der Regressionsgleichung wird der Wert der unabhängigen Variablen verändert, um etwaige Auswirkungen auf die abhängige Variable auswerten zu können. Regressionsmodelle kommen z. B. in folgenden Bereichen zum Einsatz:
- Wissenschaft
- Finanzwesen
- Online Marketing
- Markt- und Sozialforschung
Ziele der Regressionsanalyse
Mit der Anfertigung eines Regressionsmodells werden i. d. R. drei Ziele verfolgt:
- Zusammenhänge zwischen zwei oder mehr Variablen herstellen: Besteht ein Zusammenhang und wenn ja, wie stark ist er?
- Vorhersage von möglichen Veränderungen: Inwiefern passt sich die abhängige Variable an, wenn eine der unabhängigen Variablen verändert wird?
- Bestimmung von Werten zu einem bestimmten Zeitpunkt: Welchen Wert nimmt die abhängige Variable an, nachdem die unabhängige Variable neu festgelegt wurde?
Regressionsanalyse: Ziele im Online Marketing
Im Online Marketing sollen verschiedene Kanäle wie Social Media, E-Mail oder Affiliate Marketing zur Umsatzsteigerung des Unternehmens beitragen. Mithilfe von Regressionsmodellen kann analysiert werden, auf welchen Kanälen sich die Investitionen am ehesten lohnen. Dadurch können bisherige Marketingstrategien gezielt umstrukturiert und Werbebudgets angepasst werden.
Formen der Regressionsanalyse
Es gibt mehrere Formen der Regressionsanalyse. Je nachdem, wie viele Variablen zu untersuchen sind und um welchen Skalentyp es sich dabei handelt, bietet sich eine der folgenden Regressionsanalysen an:
| Form der Regressionsanalyse | Mögliche Merkmale der Variablen | Skalentyp der abhängigen Variablen (AV) | Skalentyp der unabhängigen Variablen (UV) |
|---|---|---|---|
| einfache lineare Regression |
|
|
|
| multiple lineare Regression |
|
|
|
| (binäre) logistische Regression |
|
|
|
| multinominale logistische Regression |
|
|
|
Einfache lineare Regressionsanalyse
Mit dieser grundlegenden Regressionsanalyse wird ein linearer Zusammenhang zwischen zwei Variablen modelliert. Eine Variable ist dabei unabhängig, sprich, ihr Wert kann beliebig verändert werden, wohingegen die zweite Variable von der ersten abhängig ist. Die Regressionsgleichung hierzu lautet:
y=0+1∙x
In dieser Regressionsgleichung stellt y die abhängige Variable (AV) und x die unabhängige Variable (UV) dar. β0 und β1 sind die sogenannten Regressionskoeffizienten des Modells.
Was sind die Regressionskoeffizienten?
β0 wird auch Regressionskonstante genannt und gibt den Wert der AV an, wenn die UV gleich Null ist. Eine inhaltliche Auswertung dieses Koeffizienten ist jedoch nur dann sinnvoll, wenn die UV auch in der Praxis den Wert Null annehmen kann.
β1 stellt die Steigung der Regressionsgeraden dar, sprich in welchem Ausmaß sich die AV aufgrund der UV verändert. Je größer der Zahlenwert von β1, desto stärker ist der Einfluss der UV auf die AV.
Voraussetzung für die lineare Regressionsanalyse
Damit die lineare Regressionsanalyse sinnvolle Ergebnisse zur Interpretation liefert, müssen folgende Modellannahmen gelten:
- Zwischen den Variablen besteht ein linearer Zusammenhang.
- Das Skalenniveau der AV und UV sollte metrisch sein, sprich einen konkreten Zahlenwert besitzen. Ein Beispiel dafür ist die Körpergröße.
- Die Residuen (Abweichungen) sollten zum einen keine Korrelation untereinander aufweisen und zum anderen konstant über den gesamten Wertebereich der AV streuen. Dies wird Homoskedastizität genannt.
Multiple lineare Regressionsanalyse
Mit der multiplen Regressionsanalyse kann der Einfluss mehrerer unabhängiger Variablen auf eine abhängige Variable untersucht werden. Allerdings bleibt die Annahme bestehen, dass die Zusammenhänge zwischen der AV und der jeweiligen UV linearer Natur sind. Aus diesem Grund ähnelt die Regressionsgleichung der der linearen Analyse, es wird aber für jede UV ein neuer Term hinzugefügt:
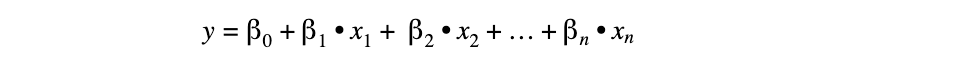
Voraussetzung für die multiple lineare Regressionsanalyse
Zwischen den einzelnen unabhängigen Variablen sollte im besten Fall keine lineare Abhängigkeit bestehen. Diese sogenannte Multikollinearität kann u. U. zu großen Standardabweichungen der Regressionskoeffizienten führen. Etwaige Einflüsse der UV wären damit nicht mehr statistisch zu erkennen.
Außerdem sollte das Skalenniveau der AV wie bereits bei der einfachen linearen Regression metrisch sein. Die UV kann dagegen auch dichotom sein und damit zwei Merkmalsausprägungen besitzen, z. B. trägt die Variable „Geschlecht“ die zwei Merkmale „männlich“ und „weiblich“.
Logistische Regressionsanalyse
Die logistische Regressionsanalyse wird meist angewandt, wenn die abhängige Variable nicht mehr metrisch, sondern diskret skaliert ist. Das bedeutet, dass die Daten über keinerlei Rangordnung oder interpretierbaren Abstände verfügen. Bei einem dichotomen Skalenniveau der AV, z. B. wenn es die zwei Antwortmöglichkeiten „ja“ und „nein“ gibt, kommt die binäre logistische Regression zum Einsatz. Die multinominale Skala lässt mehr als zwei Antwortmöglichkeiten zu, etwa „ja“, „nein“ und „vielleicht“, was die multinominale logistische Regression erfordert.
Die binäre logistische Regressionsgleichung lautet:
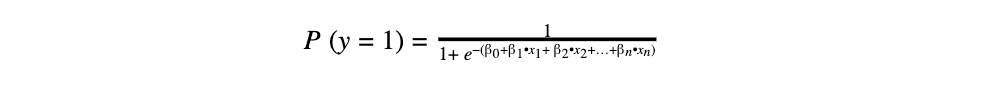
Legende:
- y: abhängige Variable mit zwei Merkmalen
- P(y=1): Wahrscheinlichkeit, dass y = 1
- e: Eulersche Zahl / Basis des natürlichen Logarithmus
- xn: unabhängige Variablen
- βn: Regressionskoeffizienten
Aussehen der logistischen Funktion
Bei der binären Regression werden die beiden Merkmale der AV mit 0 und 1 kodiert. Das bedeutet, dass die logistische Funktion auch nur Werte zwischen 0 und 1 annehmen kann. Der Graph bildet hier im Gegensatz zu den linearen Analysen keine Regressionsgerade mehr, sondern verläuft s-förmig, symmetrisch und asymptotisch gegen y=0 und y=1. Das Ergebnis der logistischen Regressionsanalyse besagt, mit welcher Wahrscheinlichkeit eine unabhängige Variable in der Bedingung der abhängigen Variable zu finden ist.
Voraussetzung für die logistische Regressionsanalyse
Auch hier sollten die unabhängigen Variablen untereinander nicht hoch korreliert sein. Außerdem gilt:
- Die abhängige Variable ist binär und 0-1-kodiert.
- Die unabhängigen Variablen sind metrisch oder im Falle kategorialer Variablen ebenfalls kodiert.
Erfahren Sie mehr über Qualtrics
Demo AnfordernBeispiel für die Regressionsanalyse
Ein Unternehmen untersucht den Zusammenhang zwischen der Zahl der Webseitenbesuche auf seiner Homepage und den Werbeanzeigen auf Social-Media-Kanälen innerhalb eines bestimmten Zeitraums. Datengrundlage bilden hier sechs Personen. Die unabhängige Variable x ist die Zahl, wie oft den Verbrauchern die Werbeanzeige ausgespielt wurde. Die abhängige Variable y ist die Zahl der Seitenbesuche.
Folgende Beispielwerte werden dafür herangezogen:
| Variablen | Person 1 | Person 2 | Person 3 | Person 4 | Person 5 | Person 6 |
|---|---|---|---|---|---|---|
| Werbeanzeige (x) | 3 | 0 | 5 | 2 | 1 | 4 |
| Webseitenbesuche (y) | 21 | 15 | 23 | 19 | 16 | 24 |
Die Funktion bzw. die Regressionsgleichung ergibt sich aus den Mittelwerten des vorhandenen Datensatzes. Im Diagramm werden diese durch die Regressionsgerade dargestellt. Aus unserem Beispiel ergibt sich anhand der Werte folgender Zusammenhang zwischen abhängiger und unabhängiger Variable:
y=15+1,77x
Ablauf einer Regressionsanalyse in der Software
Wenngleich es unterschiedliche Formen der Regressionsanalyse gibt, so ist das Vorgehen beim Erstellen eines Regressionsmodells mithilfe einer entsprechenden Software stets ähnlich:
- Datenaufbereitung: Je mehr Daten zur Verfügung stehen, desto aussagekräftiger wird das Ergebnis der Regressionsanalyse. Fehlende Datensätze können im Regressionsverfahren durch Missing-Data-Techniken ersetzt werden. Ggf. ist eine Überführung der Datenformate notwendig, z. B. beim Kodieren von nicht metrischen Variablen.
- Modellanpassung: Bereits vor der Durchführung der Regressionsanalyse sollten alle Voraussetzungen für das jeweilige Modell geprüft werden. Außerdem arbeiten einige Softwares für Regressionsmodelle mit statistischen Fehlerkorrekturen, sodass trotz Abweichungen ein vereinfachtes Ergebnis zustande kommt.
- Validierung des verwendeten Modells: Im Anschluss an die Regressionsanalyse wird geprüft, ob das gewählte Regressionsmodell den Zusammenhang zwischen den unabhängigen und abhängigen Variablen hinreichend beschreibt.
- Prognose von Werten: Sofern das Regressionsmodell den Zusammenhang zwischen den Variablen adäquat beschreibt, kann es zu Prognosezwecken eingesetzt werden. Bei Aussagen, die über den vorhandenen Datensatz hinausgehen, wird von Extrapolation gesprochen. Prognosen zu Werten innerhalb der Datensätze werden Interpolation genannt.
Interpretation der Regressionsanalyse
Statistiksoftwares geben außerdem Auskunft über:
- das Bestimmtheitsmaß (r2), auch Determinationskoeffizient genannt. Dieses gibt an, wie gut die gemittelte Regressionsgerade zu den vorhandenen Messwerten passt.
- den F-Test. Dabei wird geprüft, ob mindestens eine Variable einen Erklärungsgehalt für das Regressionsmodell liefert und es somit insgesamt als signifikant gilt.
Sind die Ergebnisse der Regressionsanalyse signifikant, können anhand der Regressionskoeffizienten Prognosen über die abhängige Variable getroffen werden. Bei der Interpretation der Ergebnisse ist jedoch stets der Unterschied zwischen Korrelation und Kausalität zu beachten. Selbst wenn Zusammenhänge zwischen zwei Variablen festgestellt werden konnten, sprich eine Korrelation besteht, bedeutet das nicht zwingend, dass sich diese gegenseitig kausal beeinflussen. Ebenso könnte eine dritte Variable für die Verteilung verantwortlich sein. Um die Vielfalt der möglichen Kausalitäten einzuschränken, gibt es z. B. weiterführende Regressionsanalysen:
- Moderatoranalyse
- Mediatoranalyse
Mit diesen wird geprüft, ob der Zusammenhang zwischen zwei Variablen von einer dritten Variablen beeinflusst wird.
Bereit anzufangen? Jetzt Demoversion anfordern!