Irrtums
wahrscheinlich
keit: Definition, Berechnung und Nutzen

Was ist die Irrtums
wahrscheinlich
keit

Bei der Irrtumswahrscheinlichkeit handelt es sich um einen Begriff der Statistik. Die Irrtumswahrscheinlichkeit gilt als Nebenprodukt statistischer Berechnungen und gibt an, um wie viele Prozentpunkte die Ergebnisse einer Berechnung vom Wert der Grundgesamtheit abweichen. Der Wert dient ebenfalls dazu, Studien transparent zu gestalten und Ergebnisse interpretierbar zu machen. In der Folge lassen sich für Unternehmen geeignete Handlungen ableiten, um etwa die Kundenzufriedenheit zu verbessern. Irrtumswahrscheinlichkeiten ergeben sich vor allem bei der Marktforschung und wissenschaftlichen Studien.

Beispiele für den Nutzen der Irrtums
wahrscheinlich
keit

Die Irrtumswahrscheinlichkeit ist Teil von Studien, die auf der Auswertung von Stichproben basieren. In diesen Stichproben werden die Befragten zufällig aus der Grundgesamtheit ausgewählt.

Für die folgenden Beispiele lassen sich Irrtumswahrscheinlichkeiten berechnen:

• Eine Sportmannschaft verfügt über eine vollständige Liste aller Personen, die im vergangenen Jahr Tickets gekauft haben. Von dieser Liste wählt die Mannschaft willkürlich einen Teil aus, um mithilfe einer Befragung zu ermitteln, wie viele der Käufer tatsächlich Fans der Sportmannschaft sind. Diese Fragestellung lässt sich mit der Berechnung des Irrtumswahrscheinlichkeit auf die Gesamtheit aller Käufer beziehen.
• Ein Unternehmen verfügt über eine vollständige Liste aller Arbeitnehmer. Von dieser werden willkürlich Mitarbeiter für eine Befragung zu betrieblichen Zusatzleistungen ausgewählt. Mithilfe der Befragung lässt sich ermitteln, ob die befragten Mitarbeiter eine geringe Bonuszahlung oder eine weiteren Urlaubstag bevorzugen. Mit der Ermittlung der Ergebnisse lässt sich die jeweilige Irrtumswahrscheinlichkeit der beiden Antwortoptionen für die Gesamtheit aller Mitarbeiter berechnen.

Berechnen Sie die optimale Stichprobengröße mit unserem kostenlosen Stichprobenrechner

Weitere Arten von Fehlern

Neben einer zu starken Abweichung der Stichprobe von der Gesamtheit, die sich in der Irrtumswahrscheinlichkeit widerspiegelt, gibt es noch einige weitere Stichprobenfehler, die das Ergebnis einer Umfrage beeinflussen können:

• Ein Coverage-Error beziehungsweise Abdeckungsfehler tritt auf, wenn im Stichprobenrahmen Teilnehmer fälschlicherweise ausgelassen oder hinzugefügt beziehungsweise doppelt aufgeführt werden.
• Non-Response-Error beziehungsweise Stichprobenausfall oder Antwortausfall entsteht, wenn Teilnehmer gestellte Fragen nicht oder nur teilweise beantworten.
• Measurement-Error beziehungsweise Messabweichung bezeichnet die Differenz zwischen Messwert und Referenzwert. Häufig resultiert diese aus fehlerbehafteten Fragebögen.

Die Irrtums
wahrscheinlich
keit berechnen

Wie sich die Irrtumswahrscheinlichkeit berechnen lässt, erklärt sich im Folgenden.

Formel zur Berechnung der Irrtums
wahrscheinlich
keit

Die jeweilige Irrtumswahrscheinlichkeit lässt sich einfach mit unserem Taschenrechner bestimmen:

Die Formel zur Ermittlung der Irrtumswahrscheinlichkeit lautet wie folgt:

Z * √((p * (1 – p)) / n)

• Z = standardisierte Zufallsvariable
• P = Signifikanzwert
• n = Stichprobengröße

Die standardisierte Zufallsvariable, die es zur Berechnung der Irrtumswahrscheinlichkeit bedarf, lässt sich in der folgenden Tabelle nachschlagen:

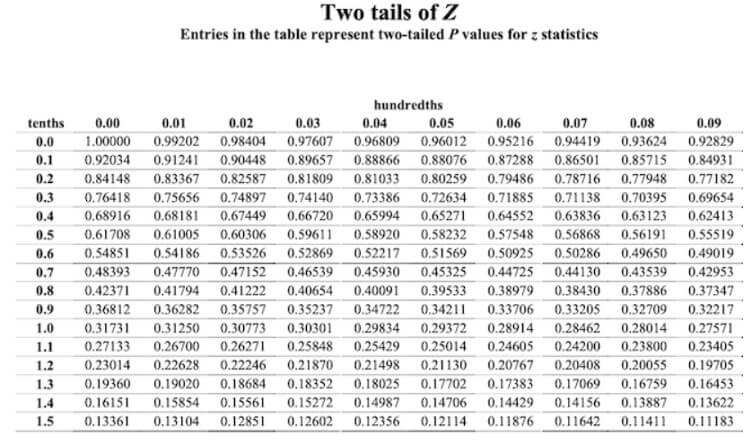
Die Vorgehensweise zur Berechnung der Irrtumswahrscheinlichkeit lautet wie folgt:

1. p von 1 subtrahieren, beispielsweise wenn p = 0,05, dann 1-p= 0,95.
2. 1-p mit p multiplizieren, beispielsweise 0,05 x 0,95 = 0,475.
3. Das Ergebnis der Multiplikation durch die Stichprobengröße n teilen, beispielsweise 0,0475 / 1000 = 0,0000475.
4. Wurzel dieses Werts berechnen, entspricht in diesem Fall = 0,0068920. Dieser Wert ist der Standardfehler des Mittelwerts.
5. Im letzten Schritt wird dieser Wert mit dem Z*-Wert multipliziert. Das entspricht in diesem Fall = 1,96. Daraus ergibt sich 0,0068920 x 1,96 = 0,0134395. Dies entspricht einem Irrtumsfehler von rund 1,3 Prozent.

Beispiel zur Berechnung der Irrtums
wahrscheinlich
keit

Zur Verdeutlichung der oben dargestellten Vorgehensweise folgt ein Beispiel.

Ein Unternehmen führt eine Umfrage unter 1000 willkürlich ausgewählten Kunden aus dem CRM durch. Die Umfrage ergibt, dass 52 Prozent bzw. 520 der Befragten zufrieden mit ihrem letzten Einkauf bei diesem Unternehmen sind. Währenddessen sind 48 Prozent, also 480 Befragte, mit ihrem letzten Einkauf in diesem Unternehmen nicht zufrieden. Für die Mitteilung der Ergebnisse an die Anteilseigner soll nun eine Irrtumswahrscheinlichkeit zu diesen Werten hinzugefügt werden. Die Berechnung geht auch in diesem Fall von einem Konfidenzintervall von 95 Prozent aus. Folglich beträgt der Z*-Wert erneut 1,96.

1. 1-p = 0,48
2. 0,52 (p) x 0,48 (1-p) = 0,2496
3. 0,2496 / 1000 = 0,0002496
4. Die Wurzel von 0,0002496 beträgt 0,01577987
5. 0,01577987 x 1,96 = 0,0309654 beziehungsweise ≈3,1 Prozent

Den Anteilseignern lässt sich nach dieser Berechnung mitteilen, dass mit 95-prozentiger Sicherheit 52 Prozent der Kunden – plus oder minus 3,1 Prozent – zufrieden mit ihrem letzten Einkauf waren.

Um diese Berechnung durchzuführen, gilt es, zwei Bedingungen zu erfüllen:

1. n x p = ≥ 10
2. n x (1-p) = ≥ 10

Die richtige Stichprobengröße wählen

Eine geeignete Stichprobengröße zur Untersuchung zu wählen ist einer der wichtigsten Prozesse bei der Erstellung und Durchführung von Umfragen, da die Ergebnisse der Umfragen möglicherweise Unternehmensentscheidungen beeinflussen. Zu kleine Stichproben hingegen verzerren das Ergebnis und liefern keine validen Daten. Je größer die gewählte Stichprobe ist, umso mehr verringert sich die Irrtumswahrscheinlichkeit. Gleichzeitig ist jedoch zu bedenken, dass die Durchführung umfangreicherer Stichproben zumeist zu erhöhten Ausgaben für das Unternehmen führt.

Die passende Stichprobengröße variiert dabei in Abhängigkeit von der Personenanzahl, die nötig ist, um die Gesamtpopulation abzubilden. Bei der Befragung britischer Arbeitskräfte ist etwa eine Stichprobe von 2.000 Personen angemessen. Um die passende Stichprobengröße zu ermitteln, bieten sich die folgenden Schritte an.

Irrtumswahrscheinlichkeit berechnen

Wie bereits beschrieben, gibt die Irrtumswahrscheinlichkeit an, in welchem Maße eine Umfrage oder Studie der Gesamtpopulation dieselben Ergebnisse hervorbringen würde wie jene der Stichprobengröße. Zur Berechnung der Irrtumswahrscheinlichkeit lässt sich die obengenannte Formel verwenden.

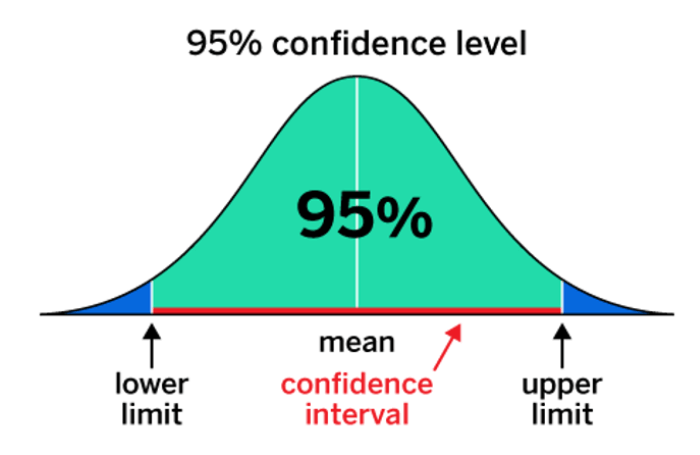
Konfidenzintervall interpretieren

Mithilfe des Konfidenzintervalls lässt sich ermitteln, wo sich der tatsächliche Mittelwert eines Datensatzes befindet. Außerdem zeigt er auf, zu welchem Grad dieselben Ergebnisse bei mehrmaliger Wiederholung der Befragung oder der Studie auftreten würden. Eine kleinere Stichprobe hat ein geringeres Konfidenzintervall zur Folge, während mit einer größeren Stichprobe ein größeres einhergeht.

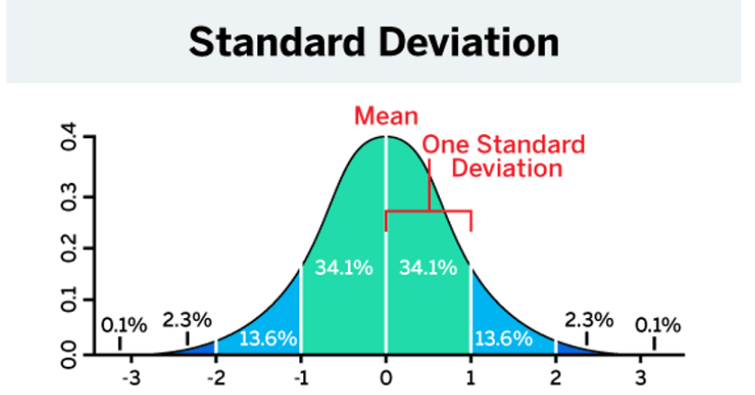
Standardabweichung prognostizieren

Die Standardabweichung sagt aus, in welchem Maße sich die durch die Teilnehmer gemachten Angaben voneinander unterscheiden. Ebenso lässt sich mit der Standardabweichung ermitteln, inwieweit diese Angaben vom arithmetischen Mittel, also dem Mittelwert oder dem Durchschnitt, differieren.

Eine geringe Standabweichung deutet darauf hin, dass sich die Werte eines Merkmals eng am Mittelwert sammeln. Eine hohe Standardabweichung steht hingegen für eine starke Streuung der Werte.

Größe der Gesamtpopulation einbeziehen

Die Größe der Gesamtpopulation bedingt in enormem Maße, wie viele Teilnehmer eine Befragung oder eine Studie benötigt, um als repräsentativ zu gelten. Dabei werden der Gesamtpopulation jene Individuen zugerechnet, deren Meinung oder Kaufverhalten die Befragung oder Studie ermitteln soll.

Nähere Informationen zur Bestimmung der geeigneten Stichprobengröße liefert zudem unser E-Book.

Die Irrtums
wahrscheinlich
keit in Umfragen reduzieren

Die Irrtumswahrscheinlichkeit zu verringern trägt in hohem Maße zur Validität der Ergebnisse bei. Diese lässt sich mit verschiedenen Methoden reduzieren.

• Anzahl der Variablen verringern: Eine hohe Anzahl an Variablen in einer Studie führt nicht selten zu einer größeren Fehlerwahrscheinlichkeit. Demzufolge ist es sinnvoll, weniger Variablen einfließen zu lassen, was gleichzeitig zu einer geringeren Irrtumswahrscheinlichkeit führt.
• Stichprobengröße erhöhen: Eine der einfachsten Möglichkeiten, die Irrtumswahrscheinlichkeit einer Befragung zu verringern, besteht darin, die Anzahl der Befragten zu vergrößern. Eine größere Stichprobe ist gleichzusetzen mit einer repräsentativeren Darstellung.
• Geringeres Konfidenzintervall nutzen: Ein niedrigeres Konfidenzintervall liefert präzisere Angaben zur Irrtumswahrscheinlichkeit. Gleichermaßen ist bei dieser Methode Vorsicht geboten, da ein geringeres Konfidenzintervall möglicherweise nicht die Gesamtpopulation abbildet.
• Einseitiges Konfidenzintervall nutzen: Im Vergleich zu einem zweiseitigen Konfidenzintervall weist ein einseitiges eine geringere Irrtumswahrscheinlichkeit auf. Dies resultiert daraus, dass einseitige Konfidenzintervalle lediglich anzeigen, ob gewählte Parameter über oder unter dem gewählten Grenzwert liegt.

Mit Qualtrics verlässliche Umfrage
ergebnisse erhalten

Möchten auch Sie Daten aus Befragungen und wissenschaftlichen Studien effizient für Ihr Unternehmen nutzen, bietet Ihnen Qualtrics mit Qualtrics CoreXM ein geeignetes Tool mit zahlreichen Features.

Qualtrics CoreXM vereint mehrere Anwendungen und Features in einer Software. Es ermöglicht Ihnen, Befragungen unter Kunden durchzuführen. Sie erhalten Echtzeit-Ergebnisse und zügige Analyse von Daten. Damit sind Sie in der Lage, zielgerichtet Maßnahmen einzuleiten und den Erfolg Ihres Unternehmens zu steigern.